一种长宽比自适应变化的目标尺度估计算法

郭静静，侯志强，陈立琳，蒲 磊，余旺盛，马素刚

(1.西安邮电大学计算机学院,西安,710121; 2.西安邮电大学陕西省网络数据分析与智能处理重点实验室,西安,710121; 3.空军工程大学信息与导航学院,西安,710077)

目前，在视觉目标跟踪[1]中，相关滤波方法以其优异的快速性和良好的跟踪性能受到研究人员的关注。Bolme等人[2]首次将相关滤波引入跟踪领域，提出误差最小平方和滤波器(MOSSE)跟踪算法，对尺度和形变的鲁棒性有较好的跟踪效果；Henriques等人[3]提出基于循环结构(CSK)的核相关滤波跟踪算法，取得良好的跟踪结果；Henriques等人[4]提出核相关滤波(KCF)跟踪算法，扩展了特征通道，提升了跟踪性能。但上述算法都是采用固定尺度因子，当目标尺度发生变化时，极易产生漂移甚至跟丢现象。

为解决跟踪过程中目标尺度变化问题，Li等人[5]提出尺度池(scale adaptive with multiple feature tracker,SAMF)方法，提高了跟踪效率，但由于其搜索范围较小，导致目标尺度定位并不准确；Danelljan等人[6]提出以KCF为基础的尺度金字塔(discriminative scale space tracking，DSST)跟踪算法，解决了尺度等比例变化的问题，但未解决目标长宽比变化问题；He等人[7]基于尺度金字塔的方法提出尺度因子为10、步长因子为1.03的跟踪算法，其尺度改进方法极大提高了跟踪精度，但仍没有解决目标长宽比变化问题；Li等人[8]提出使用4个二维相关滤波器分别定位目标上下左右边界，能较好地估计目标尺度长宽比变化，但计算较复杂。

此外，在跟踪过程中，目标和背景由于各种因素会发生变化，如果没有良好的模板更新机制，很容易导致跟踪失败[9]。Wang等人[10]提出用平均响应相关能量值(APCE)来判断当前跟踪情况，采用多峰检测机制和高置信度更新机制，提升跟踪的速度；KIANI等人[11]提出使用真实移位产生的负样本，这些样本包括更大的搜索区域和真实的背景，但当遇到背景复杂及各种干扰的情况下，易造成模板漂移，从而导致目标跟踪失败。

针对以上研究存在的不足，本文提出分层尺度估计方法，旨在解决实际跟踪中目标尺度长宽比变化问题，进一步提高跟踪算法的鲁棒性。

1 相关概念

在考虑目标尺度变化的跟踪算法中，基于相关滤波框架的算法应用广泛[12]。以DSST算法为例，其位置估计使用二维相关滤波器，计算响应值，取其最大值对应的坐标为目标的位置；其尺度估计使用尺度金字塔方法[13]，将目标进行不同尺度的放大或缩小，选择最大响应值作为最终目标的尺度，从而达到尺度自适应。本文主要考虑基于相关滤波跟踪的目标尺度估计问题。

1.1 相关滤波跟踪

相关滤波跟踪是通过大量训练样本找到一个分类器函数f(x;w)=，使得其在某种决策条件下损失最小，w为分类器函数待求参数[4]。通过将误差平方和作为损失函数，可得到w的求解形式为：

(1)

式中：xi和yi分别为训练样本和所对应的标签；λ为正则化系数。通过对式(1)求偏导，得到其解为：

w=(XTX+λI)-1XTy

(2)

(3)

1.2 DSST跟踪

DSST算法提出一种尺度估计方法[6]，该方法可以和所有相关滤波算法相结合，具有良好的通用性。

利用1.1节的相关滤波模型可以得到预测目标的位置，然后以位置估计得到的中心点构建尺度金字塔块xS，xS为33种不同尺度因子构建的训练样本集。利用尺度金字塔块计算出尺度滤波器的系数矩阵为：

αS=(KxS+λI)-1yS

(4)

式中：K表示核空间的核矩阵；yS为尺度滤波器响应值。以位置预测的中心提取金字塔图像块，并提取其直方图(HOG)特征，构成尺度样本集ZS，经过训练的尺度滤波器的回归函数为：

fS(ZS)=KxSZSΘαS

(5)

式中：αS为尺度滤波器的系数矩阵，取其函数最大值对应的尺度为下一帧目标的尺度。

2 本文算法

针对跟踪过程中尺度的精确估计问题，本文提出一种长宽比自适应变化的目标尺度估计算法，通过构建二维尺度因子来估计目标的长宽比变化，有效地解决了目标的尺度变化问题；为进一步提高跟踪算法的鲁棒性，针对模板更新问题，提出了一种新的更新策略来判断是否需要更新模板，有效避免了跟踪过程中的模板漂移问题。

2.1 尺度估计模块

尺度估计模块主要采用扩充尺度长宽因子和分层尺度估计的方法，在提高跟踪器鲁棒性的同时，还保证其具有较快的跟踪速度。

2.1.1 尺度估计中长宽因子的选取

运动过程中，相较于目标尺度等比例扩大或缩小，更容易发生尺度长宽比变化的扩大或缩小[14]。目标尺度的扩大或缩小可能会由目标平面旋转、形变等因素引起，并严重影响跟踪性能。尺度金字塔用于尺度估计的目标样本选择方法为：

I=anP×anR

(6)

为了使目标的尺度估计出现长宽比变化，本文提出了新的尺度滤波器构建方法，其尺度因子定义为：

ciP×djR

(7)

尺度金字塔与本文提出的尺度估计模块在DSST算法中的采样结果对比见图1，对于第T+1帧图片，对该图片进行m×n次多尺度采样(其中m为宽的采样次数，n为高的采样次数，m=n=35)，达到了精确估计目标尺度长宽比变化的目的；采样完成之后，对每一个图像块都提取其HOG特征，通过计算相关响应值得到最佳的尺度因子，即为第T+1帧的目标尺度。

图1 尺度金字塔与本文提出的尺度估计模块在DSST中的采样结果对比图

2.1.2 减少运算量的分层尺度估计

采用2.1.1节中尺度长宽因子的选取方法，使目标尺度估计中出现具有长宽比变化的候选框，但由于目标在运动过程中的尺度变化具有连续性，若采用35×35的尺度估计方法进行穷搜索，则会出现过多的无效采样，极大地降低跟踪速度。因此本文提出分层尺度估计来减少采样次数、提高跟踪速度。

分层尺度估计方法思路如下：以目标高方向35个尺度因子为例，首先将35个因子按数值大小分为5份，每份7个因子，选取每一份居中的因子，作为该方向粗略估计因子，宽方向因子的选取类似；然后根据两组因子的顺序组合对搜索区域进行5次等比例采样，粗略估计出目标的长宽因子，将其定位到35个因子中，选出所对应的7个因子交叉组合，进行7×7次采样实现对目标尺度的等比例变化和长宽比变化，取其最大响应值对应的尺度作为目标修正尺度因子，即目标最佳尺度，分层估计原理过程见图2。

对于一幅输入图像，第1层粗略估计只对目标进行等比例的扩大或缩小变化，首先在35个因子中选取5个作为粗略估计因子，采样结果记为F1,…,Ft,…,F5；然后提取其HOG特征，计算相关响应；最后将其最大响应值对应的因子作为粗略估计的长宽因子wt和ht，构建粗略尺度估计模板。

第2层尺度修正估计包括等比例变化和长宽比变化，以第1层为基础。图2中，只提取蓝色框的预测目标特征。第2层整体流程为：首先对第1层选取标号为t的因子，将其对应交叉组合作为修正估计因子，对目标进行7×7次采样采样过程为：对于宽方向一个固定的尺度因子，取高方向7个修正估计因子，计算其响应；然后变化其宽方向因子，循环取尽7×7个修正估计因子；最后选取最大响应值对应的尺度为目标最佳尺度wf和hf，构建修正尺度估计模板。

图2 分层尺度估计原理图

在目标尺度估计模块，仅采用扩充尺度长宽因子的方法需进行m×n(m=n=35，共1 225)次采样，而加入分层尺度估计模块后仅需计算x+k×k(x=5，k=7，共54)次，因此跟踪速度得到极大提高。

表1列出了3个原始算法的平均FPS和加入本文模块之后3个算法的平均FPS。通过实验数据得到：加入本文模块之后的算法在运行效率上均有一定程度的提高。

表1 原始算法与改进之后的算法速度对比

2.2 模板更新模块

目标在运动过程中，会出现尺度变化、旋转、遮挡等复杂场景[15]，采用一般的逐帧更新策略，会导致模板受到背景干扰，致使模板漂移严重。针对此问题，本文通过判断相邻两帧目标的差异性来对模板进行选择性更新。

(8)

式中：η为尺度滤波器的学习率。

在对目标进行分层尺度估计时，共使用2个模板，分别是粗略估计模板和修正估计模板，其模板构建方式参考2.1.2节。对于粗略估计模板，为保证目标不被跟丢，使用式(8)对该模板进行实时更新；

对于修正估计模板，为防止模板漂移，提出一种新的模板更新策略，公式为：

(9)

式中：Rt和Rt-1分为目标第t帧和第t-1帧的目标响应向量，δ的取值通过实验选取。当式(9)成立时，认为目标发生明显形变或尺度变化，对修正估计模板进行更新；反之，则不更新修正估计模板。

2.3 算法整体流程

综合本文算法关键部分的描述，主要跟踪步骤见表2。

表2 一种尺度长宽比自适应变化的目标尺度估计算法

图3 加入本文模块的HCF算法框架图

3 实验结果分析

在Window7系统下，采用MATLAB 2016Rb进行编程实现本文算法。实验在配置为Intel(R)Core(TM)i7-6 850k 3.6 GHZ处理器，内存为16 GB，GPU为NVIDIA GTX 1080Ti的电脑上进行测试。

通过大量实验结果对比和分析，最终加入本文模块的DSST、HCF[16]和OSA[17]算法中的尺度因子a和采样个数S分别设定为a=1.02，S=35。粗略估计尺度因子Sc=5，其值固定不变，为{1.319 5,1.148 7，1，0.870 6，0.757 9}，修正估计尺度因子Sf=7，其值根据粗略因子变化。其中DSST中δ=0.5；HCF中δ=0.1；OSA中δ=0.5。

利用OTB100测试本文算法的有效性，将本文算法的模块引入到3个跟踪算法中，其中3个算法中的原始尺度模块和模板更新模块使用的方法见表3，将本文提出的模块替换原始算法的模块。

表3 3种算法原始的尺度和模板更新模块

3.1 定性分析

为充分说明本文提出模块的有效性，将本文算法作为新的模块加入DSST、HCF和OSA中，将新的算法分别命名为DSST_Ours、HCF_Ours和OSA_Ours。图4给出了3种原算法以及其改进后算法跟踪结果，其中红色为本文提出的算法跟踪结果，绿色为3种原算法跟踪结果，左上角数字为视频帧数。从以下2个方面对算法进行定性分析：

1)快速尺度变化。以视频CarScale、Car4和MotorRolling为例。在跟踪过程中出现快速尺度变化去情况，虽然3种算法都能始终跟踪目标，但不能解决目标尺度长宽比问题，在引入本文尺度模块后，能达到目标尺度自适应的效果。特别是在视频MotorRolling中，目标尺度大小交替变化，本文算法能很好的适应尺度变化。

2)目标遮挡。以视频Lemming、Tiger2和Liquor为例，目标在跟踪过程中有不同程度的遮挡，跟踪算法不能很好地获取目标信息甚至获取错误的信息，致使跟踪失败。在视频Liquor中，由于遮挡情况导致目标跟踪错误，而本文算法提出的模板更新策略，避免了遮挡情况对跟踪结果的影响，因此本文算法对目标遮挡问题有较好的鲁棒性。

图4 3种跟踪算法实验结果对比图

3.2 定量分析

根据2种标准对跟踪器性能进行了评估，即精度和成功率[18]。图5表示在OTB100上，3种原算法和加入本文模块之后3种算法的精度和成功率图。

表4和表5分别为3种算法在不同属性的视频中精确度对比结果和成功率对比结果。表格第1行代表不同属性的缩写，其中，各属性及缩写分别为：尺度变化属性SV、平面外旋转属性OPR、平面内旋转属性IPR、遮挡属性OCC、形变属性DEF、快速运动属性FM、光照变化属性IV、背景复杂属性BC、运动模糊属性MB、视野外属性OV、低分辨率属性LR。本文算法相较于原始算法在各种属性中表现良好，特别是针对与尺度长宽比变化相关的属性(如SV、OCC)，本文算法跟踪效果明显优于其原始算法。

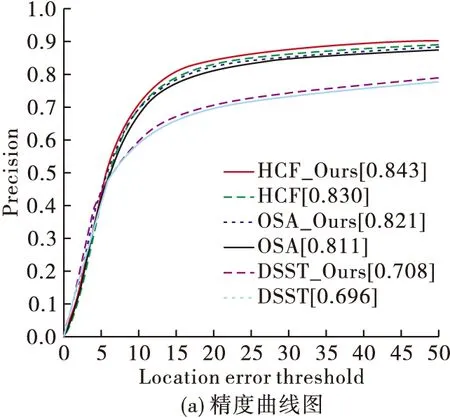
图5 OTB100上3种算法的精度和成功率

表4 不同属性下算法的跟踪精确度对比结果

表5 不同属性下算法的跟踪成功率对比结果

3.3 与主流跟踪算法的比较

为验证本文算法的有效性，将HCF_Ours与几种性能较好的算法作对比：Staple[19]、LCT[20]、KCF、MEEM[21]、DCFNet[22]、HDT[23]。因为本文提出的方法是基于相关滤波的，所以我们选取的对比算法也多是基于相关滤波算法。实验证明，本文算法与近年来的相关滤波算法相比有较好的结果，其精度和成功率见图6。

图6 OTB100上不同算法的精度和成功率

4 结语

本文提出一种尺度长宽比自适应变化的目标尺度估计算法。基于尺度金字塔方法，通过二维目标尺度因子，并采用分层尺度估计，有效解决了尺度长宽比变化问题。同时，提出一种新的模板更新策略来对模板进行选择性更新。实验结果表明，该算法在成功率和精度上都有提高，特别在目标尺度长宽比变化和遮挡场景下，本文提出的算法模块能准确跟踪到目标。

同时在实验中发现，对于Driving等视频序列，不只有尺度变化会影响跟踪结果，目标旋转也是影响跟踪结果的一个重要因素，当在跟踪过程中出现旋转场景时，会导致目标框跟踪不准确，甚至跟踪失败。在接下来的工作中，如何解决跟踪过程中出现的旋转[24]问题，将是我们下一个研究的重点方向。