基于混合改进鸟群算法的贝叶斯网络结构学习

陈海洋，张 娜

(西安工程大学电子信息学院，西安，710048)

贝叶斯网络(Bayesian networks,BN)通过概率统计将具体问题进行数据学习后再进行不确定性推理，近年来被广泛应用于故障分析、数据分析决策、目标识别、态势评估等[1-3]领域。BN结构学习是BN学习中极其重要的一部分，是通过已知的数据来确定一个最符合数据变量之间连接关系的有向无环图。BN结构学习方法主要分为3种：①基于约束的结构学习法(constraint-based methods)：该类方法对个体独立性检验的失败比较敏感，会因某次失败而导致整个网络的构建失败；②基于评分函数的结构学习法(score-search methods)[5-7]：单纯通过该方法学习BN结构精确度低、易陷入局部最优，且考虑所有可能的模型耗时长、效率低；③混合法(hybrid methods)[8-10]：常规混合法易陷入局部最优，搜索效率低。这也正是BN结构寻优中最常见缺陷。使用好的仿生智能算法可以很大程度避免陷入局部最优[11-13]。文献[14]提出生成较优初始种群的方法，并利用改进鲸鱼寻优算法进行贝叶斯网络结构寻优。该方法的寻优效率和准确度都比较好，但复杂度很高。文献[15]提出用改进后的粒子群算法(particle swarm optimization，PSO)进行BN结构学习，用互信息(mutual information)约束初始网络后，通过改进的粒子群算法搜索最优贝叶斯网络，提高了寻优效率，但由于算法不稳定，因此无法保证结构的精确率。

针对上述情况，本文提出将鸟群算法(bird swarm algorithm，BSA)[16-19]应用到BN学习，提出基于混合改进鸟群算法的BN结构学习算法。

1 基于混合改进鸟群算法的贝叶斯结构学习算法

1.1 算法的基本思想

在BN结构学习过程中，可以通过初始数据判断出节点之间的依赖关系，并用互信息将2个随机变量之间的依赖度用数值准确地表示出来，如果互信息值越大，两个变量之间存在连接边的可能性就越大。因此，输入一个BN结构的数据，根据各变量之间互信息的值判断出最优BN结构的候选边，以此构建初始结构，并生成基于鸟群算法的结构搜索空间。为了提高寻优效率，对鸟群算法做了以下改进：①加入自适应权重，动态调整收敛速度；②改进乞食者和生产者的划分方式，有利于精准寻优；③根据鸟群的适应度变化差进一步调整自适应权重，减小搜索空间。利用改进的鸟群算法作为搜索策略，并用BIC评分函数对每次更新并处理非法结构[15]后的有向无环图进行评分，直到迭代次数达到上限，输出BIC评分最优的结构即为搜索的最优BN结构。

1.2 用互信息构建初始网络

互信息是度量2个随机变量之间依赖程度的数学量。依赖程度越强，互信息值就越大。本文算法通过约束初始网络结构，为改进鸟群算法寻优BN结构提供一个较优的结构空间。

下面给出互信息约束生成的初始网络伪代码：

Mutual Information(D,G0,α)

输入：关于节点X1,X2,…,Xn的数据D，根据数据D随机生成的初始网络G0，α为一个常数，maxI(Xi)=0

输出：互信息约束生成的网络G1

fori=1,2,…,n

for(除去Xi的节点Xj)

计算节点Xi与节点Xj之间的互信息I(Xi,Xj)

if maxI(Xi)≤I(Xi,Xj)

maxI(Xi)←I(Xi,Xj)

end if

end for

end for

fori=1,2,…,n

for(每个I(Xi,Xj))

ifI(Xi,Xj)≥αmaxI(Xi)

G0中加入Xi与Xj之间的连接边

end if

end for

end for

G1←G0

returnG1

1.3 改进的鸟群算法作为搜索策略

用互信息约束生成初始网络之后，本文以改进的鸟群算法作为搜索策略。根据每只鸟在自然界觅食、警戒和迁徙等行为的位置移动更新BN结构。下面给出根据鸟群仿生行为简化的经典鸟群算法规则：

规则1：每只鸟随机选择觅食或保持警觉行为。

规则2：若选择觅食，每只鸟会记录并更新其搜索到的最佳觅食位置，并将该最佳位置分享至整个种群。然后，判断种群最佳觅食位置并记录下来，根据自身最佳与种群最佳确定下一处觅食。

规则3：若保持警觉，每只鸟为了避免被捕食者追捕，都会试图飞往种群的中心位置寻求保护，因此就会在种群内部产生竞争，食物储备多的鸟有更大概率飞往中心。

规则4：鸟群按一定的周期飞往另一区域进行觅食，鸟群中的每只鸟会分享自己觅食信息，食物储备多的鸟会带领食物储备少的鸟去寻找食物。

规则5：将食物储备最多的鸟称为生产者，最少的则为乞食者，其他鸟随机作为二者之一。乞食者会随机跟随一位生产者学习觅食方位与位置。

根据规则1～5，将鸟群生物行为分为3种：觅食行为、警戒行为、飞行行为。在此基础上，对经典鸟群算法进行3部分改进：①在觅食行为中加入自适应权重；②改变经典鸟群算法中乞食者和生产者的划分方式；③根据鸟群的适应度的变化差调整自适应权重。

1.3.1 觅食行为

根据规则1，鸟群中的每只鸟都会以相同的可能性在(0,1)之间产生一个随机数，若该数大于常数P时，选择觅食；若该数小于常数P时，则保持警觉。若选择觅食，规则2由式(1)表示。在觅食行为中，每只鸟只会依据自己上个时刻的位置经验去更新位置，这样会降低整体鸟群搜索空间的自适应性。为此，改进算法通过在每只鸟的位置更新公式前乘以一个自适应惯性权重w(如式(2)所示)来解决这一问题。通过对参数w的调节，控制鸟群的全局搜索能力与局部搜索能力，w较大时，鸟群算法的全局搜索能力强，能够跳出局部最优，提高算法搜索能力。w较小时，局部寻优能力加强，提高算法的收敛速度。随着迭代次数增加，w呈线性递减，鸟群渐渐走向中心位置的最优鸟，见式(1)：

(1)

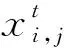
(2)

式中：t是当前迭代次数；tmax代表最大迭代次数；wmax表示初始惯性权重，通常取为0.9；wmin表示鸟群最大迭代次数的惯性权重，通常取0.4。

1.3.2 警戒行为

根据规则3，每只鸟飞往种群的中心位置过程中会与其他竞争者比较食物储备量，依据比较结果，慢慢飞往种群中心位置，这种行为可由式(3)表示。

(3)

其中

(4)

(5)

meanj为鸟群的平均位置；k是[1,N]之间的随机整数，且k≠i；N为种群规模；a1,a2是[0,2]之间的常数；pFiti为鸟i的适应度值；ε是计算机中最小的数，用来避免零分割；sumFit为鸟群的适应度之和。

1.3.3 飞行行为

规则4和规则5划分乞食者与生产者的划分方式不利于BN结构学习的精准寻优。因此，在算法改进时，改变了划分方式，即当鸟i的适应度值小于鸟群平均适应度值meanFit时，则称鸟i为生产者；反之，为乞食者。划分后，生产者和乞食者的行为分别由式(6)和式(7)描述。

(6)

(7)

式中：rand(0,1)表示产生服从高斯分布的一个随机数；k∈[1,N]，且k≠i；FL(FL∈[0,1])表示乞食者跟随生产者寻找食物的概率。

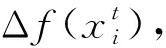
(8)

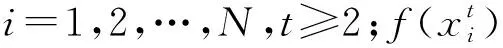
1.4 用BIC评分函数度量BN结构

本文提出的算法中，鸟群根据适应度值衡量当前网络结构与初始数据的拟合程度，用贝叶斯信息准则(Bayesian information criterion，BIC)作为适应度函数pFit。根据BIC评分结果更新有向无环图，并判断出最优BN结构。BIC评分函数可以度量结构G相对于数据D的优劣：

(9)

式中：随机变量Xi共有ri个取值1,2,…,ri，其对应的父节点π(Xi)的取值共有qi个，即1,2,…,qi。

1.5 基于混合改进鸟群算法的BN结构学习步骤

本算法步骤流程见图1。

图1 基于混合改进鸟群算法的BN结构学习流程

2 仿真结果及分析

2.1 测试函数仿真验证

为了验证改进算法的有效性，用测试函数将该算法分别与经典鸟群算法、粒子群算法进行比较，见表1。在本次实验中，群体规模均为20，维度大小为20，最大迭代次数为1 000。通过比较取得最好值和最差值、均值、标准差来证明算法的有效性，3个算法的相关参数设置见表2，实验结果见表3。

表1 测试函数表

表2 3个算法的相关参数设置表

表3 测试函数检测结果表

从表3中得出，本文算法和经典鸟群算法经过迭代后，都找到了最优值0，而粒子群算法没有，所以本文算法与经典鸟群算法在寻优能力上都优于粒子群算法，并且本文算法在最差值、均值、标准差方面都相对最低，寻优能力更高。将3个算法在测试函数的寻优过程用图2～4表示。可以看出，本文算法在3个函数的寻优中都较快找到了最优值0，寻优效率高于其他2种算法。进一步可以说明在迭代过程中动态调整搜索空间后，本文算法的搜索能力更强，且收敛性也进一步提高。

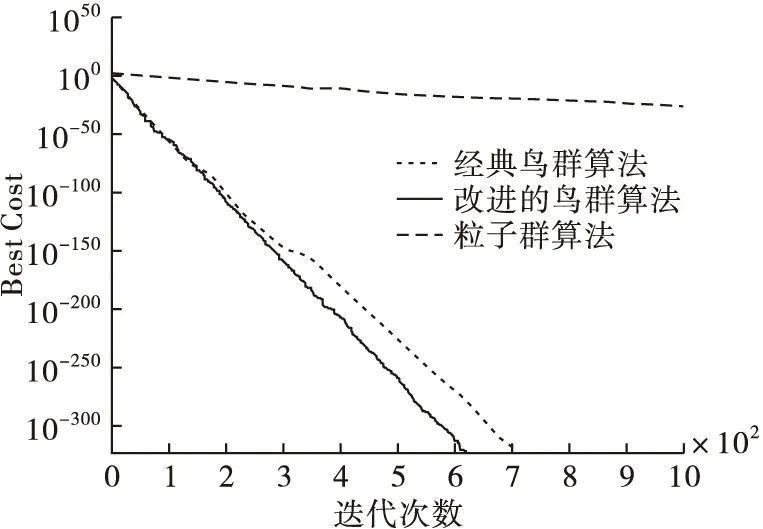
图2 3个算法在Sphere函数中的寻优过程比较

图3 3个算法在Matyas函数中的寻优过程比较

图4 3个算法在Zakharov函数中的寻优过程比较

2.2 BN结构学习仿真验证

为了验证基于混合改进鸟群算法的BN结构学习的寻优准确性、全局收敛性，把它与经典鸟群算法、粒子群算法、K2算法、MCMC算法的BN结构学习进行比较，将这5种算法分别应用于动物特征(AC)网络(7个节点，6条有向边)与胸部诊断(ASIA)网络(8个节点，8条有向边)。这两种网络分别产生数据量为100个、500个、1 000个、3 000个的样本各10组。将算法在每组数据样本上独立运行10次，每次迭代50次，结果取平均值。本文算法参数设置为种群规模=20，α=0.6，FQ=3，a1=a2=1，C=S=1.5，FL∈[0.5,0.9]，P∈[0.8,1]，粒子群算法、经典鸟群算法参数设置见表2。K2算法的节点序为互信息生成的候选边的随机节点序，MCMC算法参数为贝叶斯工具箱默认参数。贝叶斯网络结构学习算法的常用度量指标见文献[20]。仿真结果如表4和表5所示。

由表可知，本文算法的C值均大于经典鸟群算法、粒子群算法、K2算法、MCMC算法。本文算法的FA、FM、FR、F各值也都小于其他4个算法的值。从C列与F列可以看出，随着数据量的增大，本文算法的C值逐渐增大，F值逐渐减小，说明得到的BN结构越来越接近标准结构。从两个网络的BIC列值可看出，在数据量较小时，本文算法的BIC评分优于经典鸟群算法、粒子群算法、MCMC算法，但稍低于K2算法，这是由于提前给定了K2算法的节点序列，而在实际应用中，很难较准确地给出。但是随着数据量的增加，本文算法的BIC评分超过了K2算法，为了进行更细致地分析，现将2个网络中500、1 000、3 000数据量下的BIC评分值进行比较，结果见图5。

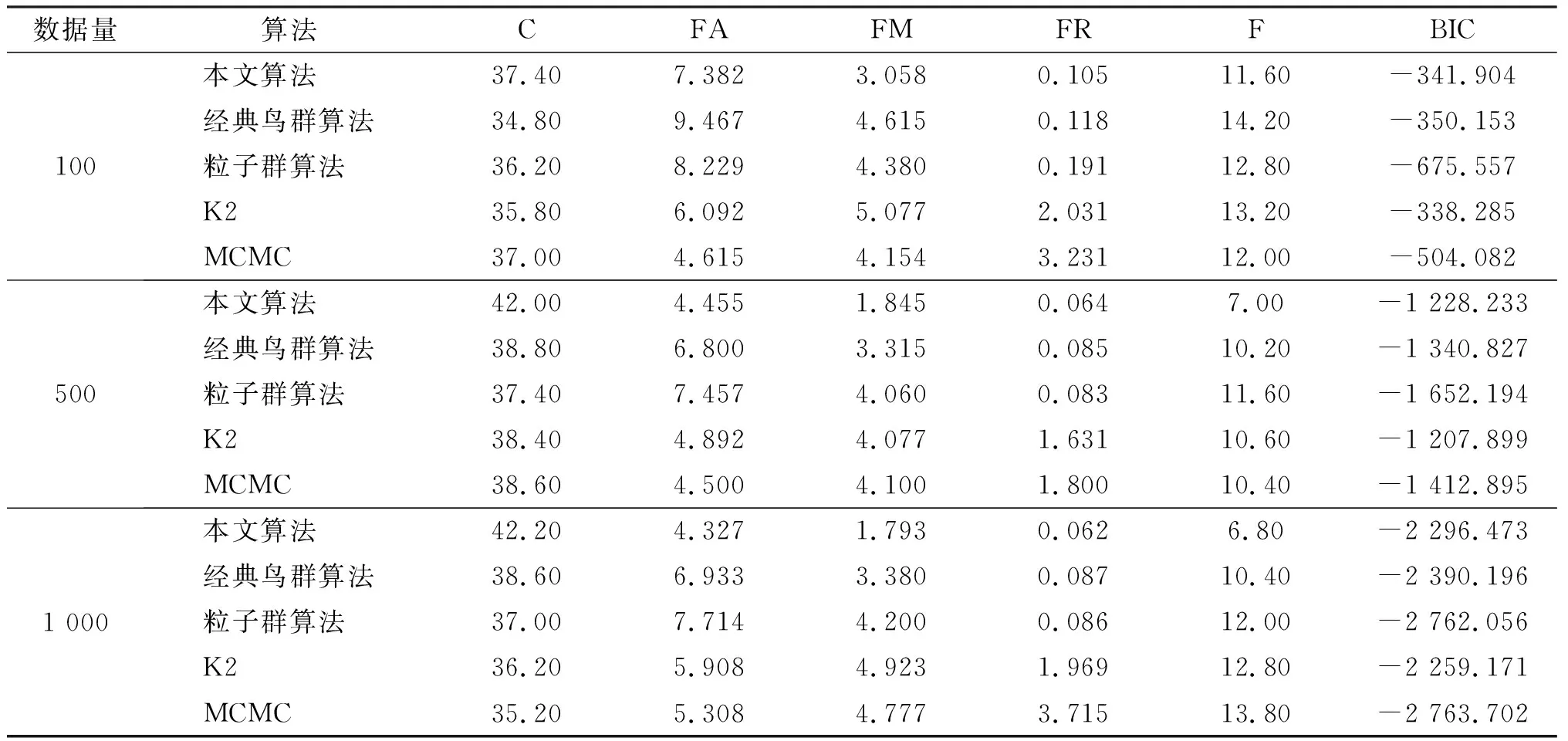
表4 不同算法在动物特征网络中的对比

续表

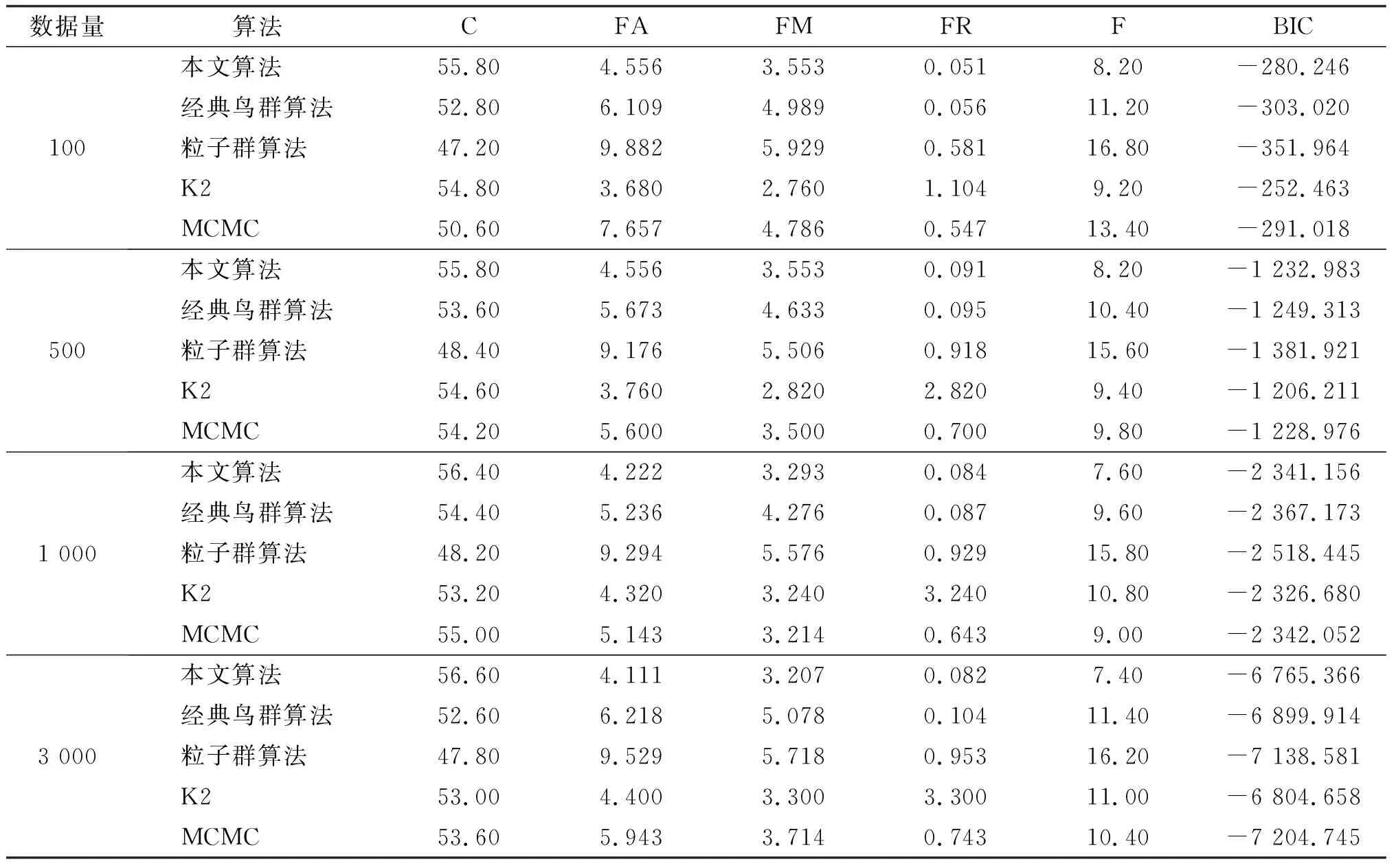
表5 不同算法在胸部诊断网络中的对比

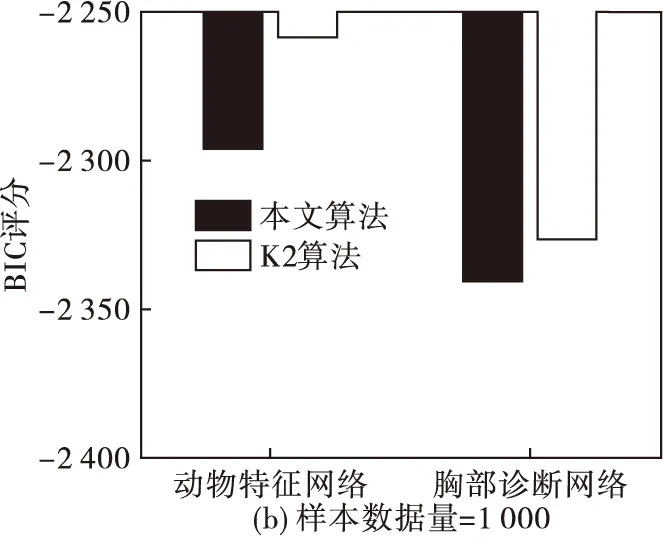
图5 不同数据量下本文算法与K2算法在动物特征网络与胸部诊断网络中的BIC评分比较

从图5可以看出，当数据量为500、1 000时，K2算法的BIC评分要稍微大于本文算法，但数据量增加为3 000时，本文算法的BIC评分较大。这就说明当数据量较大时，本文算法的结果更拟合初始数据样本。同时，为了进一步体现本文算法较其他仿生算法的搜索能力及收敛过程，分别在数据量为100、500、1 000、3 000的情况下，将本文算法与经典鸟群算法、粒子群算法在动物特征网络应用中的BIC评分在迭代过程中的变化进行比较，结果如图6。可以看出，在相同数据量下，本文算法的在搜索过程中逐步优于其他两个仿生算法，并且随数据量的增加，优势更加明显，说明本文算法在BN结构的应用中较其他算法寻优能力高，收敛性好。

图6 不同数据量下3个算法的BIC评分比较

综上所述，本文算法在6个度量BN结构学习的常用指标上都优于经典鸟群算法、粒子群算法、K2算法、MCMC算法。说明本文算法用互信息生成的初始网络，缩小了搜索空间。同时改进的鸟群算法也在全局性和局部性中保持了良好的平衡，为搜寻最优网络提供了一定的保障。

3 结语

目前，混合智能仿生算法成为了BN结构学习中的研究热点，该方法既利用了约束生成的初始网络，又利用了智能算法不易陷入局部最优的优点，从而有效改善了BN结构学习寻优效率低下、易陷入局部最优的缺陷。本文提出的基于混合鸟群算法的BN结构学习，通过互信息约束初始寻优网络，为搜寻最优网络结构提供了较好的搜寻空间。同时引入自适应惯性权重，动态调整鸟群算法的收敛速度，优化了易陷入局部最优问题，提高了寻优效率。实验结果证明，本文提出的算法准确率高，寻优性能好。