三维机场净空应用模型研究

耿 昊,蔡良才,邵 斌

(空军工程大学航空工程学院，西安，710038)

机场净空条件是机场选址阶段主要的评价指标之一。同时，在机场建成后，机场净空区内障碍物高度的控制管理也是保障机场安全运行的一项重要内容。因此，机场净空评定工作始终贯穿于机场建设与使用管理的过程中，受到了很大的关注。尤其随着计算机的普及，各种适合于机场净空评价的软件与技术不断被发掘，机场净空评价的效率、评价结果的准确性、易读性不断得到提升。目前既可以利用ClearFlite软件识别评定机场周边地形的超高情况[1]，也可以利用Triangulated Irregular Network model(TIN)构建机场周边地形和机场净空模型[2]。同时，由于ArcGIS软件具有空间分析、可视化等功能，国内外有关学者充分利用GIS的地理信息数据建模、空间分析、三维可视化等功能，提出了进行机场净空评定的思路和方法[3-11]。但是在机场净空建模中，并未对机场净空规定进行深入的解析，上述研究大都假设升降带为理想水平面，未明确分析跑道纵坡不同对机场净空区障碍物限制面以及净空评定工作所带来的影响，而根据军用机场净空规定和民用机场净空规定，在实际应用中，这些都应考虑在内[12-15]，否则，会给飞机起降安全带来一定的隐患。

因此，为使机场净空评定工作更加贴合实际，准确高效地使用机场净空规定，切实保障机场运行安全，本文提出机场净空理想模型和应用模型的概念。并以军用二级机场净空区为例，建立适用于两种模型的三维立体块净空评价模型，在分析应用模型控制点坐标以及构建净空区各组成部分三维立体块的基础上，编写机场净空评价程序，从而可以针对实际情况，快速实现机场净空区物体超高情况的评定。

1 机场净空应用模型与理想模型

为能同时保障跑道两端两侧的飞机起落及滑跑安全，机场净空区是先以跑道中线为基准，两侧各100 m的中线平行线和两端各100 m处中线水平延长线的垂直线构成升降带，再由此向四周对称拓展延伸的一个空间区域，由设定的障碍物限制面限制物体高度[13]，如图1所示。所以，跑道的纵坡构形将会影响障碍物限制面的形状，如表1所示。

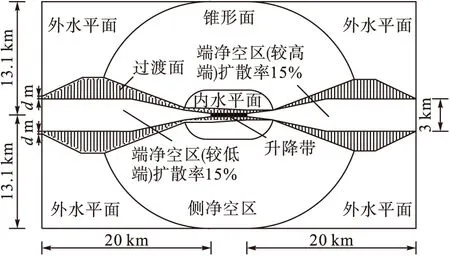
图1 机场净空区平面图(以二级机场净空区为例)

表1 机场净空理想模型与应用模型对障碍物限制面的影响

根据机场净空规定，①当跑道纵坡变化时，由于组成跑道各段坡度的差异，升降带为一系列的折面，如图2所示[16]。②以二级机场为例，图中假设跑道两端中点相差x(单位m，下同)，由于内水平面的起算高程采用的是跑道两端中点高程较高者，则内水平面高度为(60+x)m，相应的外水平面高度也应在其原限制高度380 m基础上加x。③假设升降带上任意一点a相对于跑道较低点的高度为ha，对应的过渡面与内水平面的交点为b，该点在平面上的投影为b′，根据升降带两侧过渡面起算高程采用的是跑道中线上各点的高程，则点b′到点a的水平投影距离为lab′=(60+x-ha)/(1/10)，因此，当跑道纵坡变化时，即ha连续变化，lab′连续变化，对应的内水平面与升降带两侧的过渡面交线为一系列的折线，相应的过渡面则由类似于折扇形式的一系列斜平面组成。④根据端净空区障碍物限制面起算高程为跑道端中点高程，当跑道两端中点高程不相等时，由于端净空区还是按照原先的坡度和长度扩展，外水平面高度为(380+x)m，因此，在跑道较高端，端净空区末端高度与外水平面高度相等；在跑道较低端，端净空区末端高度低于外水平面限制高度，如图3所示；反映在净空区平面上，在跑道较低端，过渡面不与端净空区末端相交，而且从升降带端开始，对应于跑道较高端端净空区两侧过渡面与内水平面、锥形面、外水平面交线，跑道较低端向两侧扩散d=x/(1/10)，如图1所示。所以，当考虑跑道纵坡变化时，升降带是由不同坡度的平面所组成的折面，会使其余障碍物限制面的范围和高度产生一系列的变化，此时，净空区只关于跑道中心点两侧对称，而在两端方向上则对称相似，以此建立的净空模型称为应用模型。

图2 升降带两侧过渡面

图3 1/2机场净空区立面图(以二级机场净空区为例)

当跑道中线上各点高程相等时，升降带为一水平面，过渡面是单独的一个斜平面，同时内水平面与升降带两侧过渡面的连线为一条直线，而升降带两端的端净空区末端高度与外水平面限制高度相等，此时，净空区关于跑道中心点两端两侧高度对称分布，以此建立的净空模型称为理想模型。

由此可见，应用模型与理想模型会对机场净空区障碍物限制面的组成产生不同的影响，进而影响机场净空区的物体评价高度：对于应用模型，应根据物体所处的净空区域计算相对高度作为评价高度，在端净空区，评价高度由物体实际高程减去相应跑道端中点高程；在升降带两侧过渡面，评价高度由物体实际高程减去跑道中线上各点的高程，在侧净空区其他障碍物限制面，评价高度由物体实际高程减去跑道两端中点的较高点高程，再评价超高情况。而对于理想模型，直接由物体实际高程减去跑道中心点高程计算相对高度，再与障碍物限制面高度对比评价超高情况。

2 机场净空三维立体评价模型

2.1 机场净空三维立体的划分

应用模型和理想模型会影响障碍物限制面的组成，进而影响机场净空评定结果，为此建立机场净空模型进行分析。由于机场净空区是一个由平面和高度限制要求所围成的三维立体空间，所以，可以将其看成由净空三维立体块组成。按照障碍物限制面的不同对机场净空三维立体进行划分，建立机场净空三维立体模型。当评价障碍物是否超高时，则只需判断该障碍物是否在机场净空三维立体块内。

以二级机场净空区为例，首先确立以跑道中心点为坐标原点(0,0,0)的机场坐标系O-XYZ，其中，X轴沿跑道中线方向，Y轴垂直于跑道中线，Z轴垂直于XOY平面向上。分析1/2机场净空区障碍物限制面，如图3所示，在理想模型中，障碍物限制面都是关于Y轴对称分布的，对应1/4机场净空区障碍物限制面，主要由15个不同的区域组成，分别用Si(i=1,2,…,15)表示，其中S14是圆锥面，其余都为平面，也就对应了15个净空三维立体块，分别用Vi(i=1,2,…,15)表示。在应用模型中，跑道纵坡由多段坡度组成，在1/2机场净空区中，除升降带、升降带两侧过渡面、内水平面的形状因跑道坡度的变化而有所突变外，其余的障碍物限制面都是关于Y轴对称相似的。因此，对于升降带S1、升降带两侧过渡面S6、内水平面S12应根据实际的跑道纵坡组成进行分析；对于其他障碍物限制面的建模则应根据跑道两端中点高程做出相应调整。

2.2 机场净空三维立体块评价模型

2.2.1 高度限制范围解算

如果Si为n边形，由机场净空区障碍物限制面的要求可以推算得出其n个角点的三维坐标，据此可以确定该净空立方体块Vi中的物体高度限制范围以及所属的平面区域。

在建立的空间直角坐标系O-XYZ下，假设平面Si任意3个角点的坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3)，根据点法式平面方程的定义，平面Si中Z坐标的表达式为：

Zi=z1+{[(y2-y1)(z3-z1)-(z2-z1)(y3-y1)]·

(x-x1)+[(z2-z1)(x3-x1)-(x2-x1)(z3-z1)]·

(y-y1)}/[(y2-y1)(x3-x1)-(x2-x1)(y3-y1)]

(1)

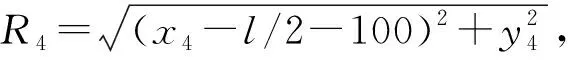
(2)

式中：k为障碍物限制面的坡度；l为机场跑道长度，单位为m。

那么，所有净空三维立体块Vi所允许的物体相对高度范围为：

z≤Zi

(3)

式中：z为Vi所允许的物体相对于跑道中心点的高度，单位为m。

2.2.2 平面限制范围解算

将Si向XOY平面垂直投影，所围成的区域即为Vi中障碍物所属的平面区域。对于平面Si，按顺时针依序编辑角点的坐标为(xu,yu),(u=1,2,…,n)，相邻的2个角点可以确定一条直线，对应n-1条的直线方程为：

(y-yu)(xu-xu+1)-(x-xu)(yu-yu+1)=0，

(u=1,2,…n-1)

(4)

其中，第n条直线方程为：

(y-y1)(x1-xn+1)-(x-x1)(y1-yn+1)=0

(5)

应用线性规划理论，由公式(4)和(5)可以将n个角点所围成n边形的投影区域表示出来。

对于圆锥面S14，在XOY平面上的投影为扇形，假设扇形内任一点(x,y)对应的半径为R，其圆心坐标为(l/2+100,0)，则此扇形的圆曲线可表示为：

(x-l/2-100)2+y2=R2

(6)

结合S14对应的投影直线方程，可以确定V14中障碍物所属的平面区域。

最终，由公式(3)和Si所围的平面投影区域，可以确定Vi所围的空间范围。

3 机场净空应用模型解析

3.1 升降带跑道中线上的坡面控制点

升降带S1在理想模型是没有高度变化的水平面，而在应用模型，受跑道纵坡的影响，由多段坡面组成。下面针对应用模型，分析升降带跑道中线上的坡面控制点。假设跑道由m段纵坡组成，每段纵坡的长度为lj，对应的坡度为μj。一般地，跑道中心点及跑道两端中点高程都为已知，分别记为hz、h1、hm+1。当j=1时，对应跑道左端中点h1，依此计算第j段纵坡末端点高程hj，作为跑道坡面控制点。而对于升降带，还应包括跑道两端各100 m的延长段，其坡度为0，且与每端中点高程对应相同。此时，两延长段的长度分别为l0=lm+1=100 m；坡度分别为μ0=μm+1=0；对应的端点高程分别为h0=h1，hm+2=hm+1，如图4所示。

图4 升降带跑道中线上的坡面图

假定以跑道左端中点作为坡面的起始点，上坡为正，下坡为负；当以跑道中心点为坐标原点，升降带跑道中线上坡面控制点的坐标为：

(7)

3.2 升降带两侧过渡面与内水平面的交点

升降带两侧过渡面S6是从升降带边线开始，按1/10的坡度向上向外倾斜，与内水平面相交所形成的平面。升降带的坡面组成会影响过渡面的平面形状，进而影响过渡面与内水平面的交点。根据“内水平面的起算高程采用跑道两端中点高程较高者”的原则，可以得到过渡面与内水平面的交点坐标为：

(8)

机场净空区障碍物限制面具有对称相似性，在应用模型中，以位于机场坐标系第一象限的障碍物限制面为例，结合障碍物限制面的角点坐标，应用式(1)～(8)，可以对15个面对应的净空三维立体块所包含的空间范围进行解算。

3.3 升降带净空三维立体块

组成升降带S1的m+2个坡面都为四边形，第j个坡面的4个角点的坐标分别为(x1(j-1),0,z1(j-1))，(x1(j-1),100,z1(j-1)),(x1j,0,z1j),(x1j,100,z1j)，则V1所围空间区域的表达式为：

(9)

3.4 端净空区净空三维立体块

在应用模型中，对于端净空区的第一段S2，起始高程应为升降带端高程z1(m+2)，以此类推，S3的起始高程为z1(m+2)+20，S4为水平面，其高程为z1(m+2)+180，S5的终点高程为z1(m+2)+380。

V3为五边形立体块，与V8、V4相接的角点坐标分别为(x1(m+2)+9 500,0,z1(m+2)+180)、(x1(m+2)+28 000/3,1 500,z1(m+2)+530/3)、(x1(m+2)+9 500,1 500,z1(m+2)+180)，其空间区域的表达式为：

(10)

3.5 侧净空区净空三维立体块

S6～S11为过渡面，起算高程从端净空区障碍物限制面S1～S5边线开始，以1/10坡度与内水平面S12、锥形面S14、外水平面S15相接。在应用模型中，S12的高程为z6(m+2)=z60，V12所围区域为：

(11)

而S15的高程为z6(m+2)+320。在此应特别注意，应用模型中，由于S15与S5通过过渡面S11联接，当S15高程与S5的终点高程相等时，V11为三角形立体块；而不相等时，V11为四角形立体块，此时V11的通用计算模型为：

(12)

式中：y101=1 500+10(z6(m+2)-z1(m+2)+140)。

对于其余净空三维立体块，参考相关文献[16]的研究成果，根据机场净空三维立体块高度和平面范围解算方法，可得其所围得空间区域。如果物体相对于跑道中心点的高度超过净空三维立体块Z坐标的表达式则视为障碍物，其超高高度为：

Δz=z-Zi

(13)

式中：Δz为超高高度，单位为m。

4 机场净空评价

4.1 机场净空评价程序

根据对应用模型的解析，针对位于机场坐标系第一象限的1/4机场净空区，依据三维立体块净空评价模型编写了机场净空评定程序，通过建立机场净空区物体高程数据库，设置不同的参数，实现净空的批量快速评定。

程序设计的主要思路是：首先，输入跑道参数与跑道纵坡段参数。对于理想模型，跑道中心点与跑道两端中点高程相同，跑道纵坡段由3段坡组成：跑道长度为一段，跑道两端的升降带各100 m为一段，坡度都为0；对于应用模型，根据物体在机场坐标系中所处的象限，需要互换跑道左右两端的中点高程，并调整对应的跑道坡度正负号和坡长。其次，填入数据。取净空区物体平面坐标(x,y)的绝对值，建立数据库。最后开始计算。先由物体高程减去跑道中心点高程计算相对高度z，利用(x,y)计算所允许的限制高度Zi，当z>Zi时，判定该物体超高，计算超高高度Δz，通过选取净空立体块，输出净空评价结果。

4.2 机场净空评定实例

某二级机场，跑道为东西方向，长度为2 500 m，机场标高为18.87 m，跑道西端20.78 m，东端16.90 m。跑道由5段纵坡组成，由西到东，跑道纵坡值依次为0.000 8，-0.003 4，-0.005，-0.003 5，0.001 8，每段坡长为600 m、500 m、450 m、400 m、550 m。建立跑道西端位于跑道中心点左侧的机场坐标系O-XYZ，机场端净空剖面图如图5所示。

图5 机场端净空剖面图(虚线代表理想模型的净空限制面,单位为m)

收集到机场周边10个典型地物点，分别采用理想模型和应用模型由机场净空评定程序对地物数据的超高情况进行判断，净空评定结果如表2所示。

表2 机场周边障碍物信息及评定情况 单位：m

由表2、图5可以发现：

1)建立的三维立体块净空评价模型不仅适用于理想模型，而且适用于应用模型。当跑道每段纵坡μj=0(j=1,2,…,m)时，即跑道中心点高程与跑道两端中点高程相等，此时应用模型变成理想模型，说明了理想模型是应用模型中的一种特殊情况。虽然按照机场净空规定，进行净空评定都应使用应用模型，但两者并不是对立的，在实际中，可以根据机场所处的寿命周期选用。在机场建设的预可行性研究阶段，根据设计的深度要求，只需提供机场可行场址的对比依据，可以使用理想模型进行净空评定；而当机场进入可行性研究阶段以后，机场跑道坡面设计资料完整具体，需要估算机场建设的工程量，并进行超高障碍物的处理，同时在机场建成投入运行以后，都必须使用应用模型进行净空评定。

2)对比地物1、2，地物3、4，地物5、6，地物7、8，位于跑道中心点两侧的障碍物限制面关于跑道中心点对称分布，因此，Y坐标的正负对机场净空评价没有影响，可以直接将Y坐标取绝对值进行评价；对于理想模型，位于跑道中心点两端两侧的升降带、端净空区、侧净空区障碍物限制高度关于跑道中心点对称相等，不会产生评定差异。

3)对比地物1、2，对于应用模型，位于跑道中心点两端的升降带、端净空区障碍物限制高度由于跑道纵坡的变化会有所不同，应加以注意，其中两端的端净空区障碍物限制高度差值为跑道两端中点高程之差，评价同一物体高程，在跑道较低端障碍物限制高度更低(严)；对于端净空区中，针对理想模型和应用模型都处于同一净空三维立体块中的物体，不同模型中障碍物限制高度不同，两者差值为相应的跑道端中点高程减去跑道中心点高程，其中跑道较低端障碍物限制高度更低(严)，如图5所示。

4)对比地物3、4，地物5、6，在跑道较低端，从升降带开始，端净空区两侧过渡面与内水平面、锥形面、外水平面交线向内dm范围，此处d=(20.78-16.90)/(1/10)=38.80 m，对于理想模型和应用模型，物体所处的净空三维立体块有所不同，对应的超高情况也不尽相同，容易造成误判，应引起注意，而对于跑道较高端，理想模型和应用模型，物体所处净空三维立体块不会有所差别。

5)对比地物7、8，在升降带两侧过渡面与内水平面交线附近，对于理想模型和应用模型，物体所处的净空三维立体块和对应的超高情况有所不同，应予以注意，避免造成误判。

6)对比地物9、10，对于位于侧净空区，针对理想模型和应用模型都处于同一净空三维立体块中的物体，不同模型中障碍物限制高度不同，两者差值为跑道较高端中点高程减去跑道中心点高程，而且应用模型的障碍物限制高度更高(松)。

5 结语

作为反映跑道坡形的升降带，将直接影响整个机场净空区的限制范围，进而对判断机场周边物体的超高情况产生一定的影响，针对上述情形，提出了机场净空理想模型和应用模型的概念，结合机场净空区的组成特点，通过划分净空平面区域，确定相应的限制高度，建立了三维立体块净空评价模型，实现了机场净空规定应用的立体化建模；同时，此模型不仅适用于理想模型，而且适用于应用模型，具有较好的通用性，更易进行程序化设计，批量评价机场净空区物体高程，使机场净空评定工作准确高效。但是，由于理想模型与应用模型在机场净空评定中存在一定的差异，适用的范围也有所不同，在机场选址以及机场净空管理中应引起足够的重视。随着国家机场建设步伐的不断加速，正确合理地使用机场净空规定控制机场周边物体高度，对于保证机场正常运行与飞机飞行安全必将产生积极的影响。