数据缺失下基于IOWA-TOPSIS的辐射源威胁评估

陈振坤,程嗣怡,徐宇恒,董鹏宇,张虎彪

(空军工程大学航空工程学院，西安，710038)

辐射源威胁评估作为电子战重要组成部分和联合作战中战场综合态势感知的关键环节，引导指挥员的决策方案制定，直接影响干扰资源分配和干扰辅助决策，是影响电子战作战效能发挥的重要因素[1]。

辐射源威胁评估可以被视为一种多属性决策问题，目前，已有模糊认知图[2]、云模型[3]、灰色关联模型[4]、广义直觉模糊软集[5]、IFE-VIKOR[6]、贝叶斯网络[7]、神经网络[8]等研究方法。以上文献的处理过程都是基于完备的信息系统，但空战电磁环境复杂、目标态势快速变化，导致侦察方难以获取完整的辐射源属性信息，辐射源威胁评估常需要在信息不完备的情况下开展；另外，对于部分辐射源目标，训练数据的不足导致一些依赖先验知识的算法难以发挥有效作用。上述文献中算法和模型的适用范围有限。

逼近理想解排序算法(technique for order preference by similarity to an ideal solution,TOPSIS)能够根据有限个评价对象与理想化目标的接近程度对评估目标进行排序，在用于旅游、资源、管理等多种领域评价评估方面时都取得良好的效果[9-12]。文献[13～15]将TOPSIS法引入到目标威胁评估问题中，设定目标评价威胁体系，建立正、负理想解，有效实现了目标威胁评估。但TOPSIS法也存在不足，传统TOPSIS模型属性权重确定较为依赖专家系统和先验知识，使权值赋予带有较大随意性和主观性；但针对辐射源威胁评估这类复杂问题，单纯的客观计算受限于公式对实际情况的拟合程度，但在辐射源威胁评估这类具有较强不确定性的问题中，其结果往往与实际情况不符，尤其是在数据又存在缺失的情况下，评价方的主观判断对提升处理结果准确度是很有帮助的。同时，TOPSIS方法评估过程与原始数据联系紧密，对数据变化敏感的特点，不具备处理存在数据缺失情况的能力。文献[16]改进TOPSIS模型实现威胁评估，但是评估过程直接略过缺失数据，导致信息量的浪费，使分析不完整。

针对上述TOPSIS法存在的问题，本文利用变异系数法(coefficient of variation,CV)对G1法进行改进，在将评价者主观认知纳入考量的基础上，反映原始数据客观差异性和信息量，实现权值的定量计算。同时，本文引入基于诱导有序加权平均算子(induced ordered weighted average,IOWA)的空值估计算法[17]实现传统TOPSIS方法在数据缺失情况下的拓展，整合数据间的相互关联中隐含的信息量，补全辐射源信息空值。IOWA算子相对于其他传统估值方法，计算速度快，能够保证时效性，得到的估值与数据关联更紧密，可靠性高。基于上述分析，本文提出一种基于IOWA-TOPSIS的评估算法，用于解决数据缺失下辐射源威胁评估问题。

1 基于组合赋权TOPSIS的辐射源威胁评估

1.1 基于TOPSIS的辐射源威胁评估

TOPSIS算法是根据有限的评价对象与正、负理想解之间相对距离的大小对评估对象进行排序的方法，适用于多属性决策。目前，TOPSIS算法在不同领域评估问题中均有运用，利用TOPSIS算法能充分利用原始信息数据，得到与实际情况相吻合的结果。

定义1[17]信息系统可以表示成一个四元组I=(X,Y,V,f)，其中：X={x1,x2,…,xm}是对象集；Y={y1,y2,…,yn}是属性集；V=VY是属性的值域；f:X×Y→V成为信息函数，即每个对象在每个属性上都有一个信息值，且∀x∈X,y∈Y,f(x,y)∈V。

算法具体步骤如下：

Step1接收机侦收未知辐射源信号后，通过整理得到不同的辐射源参数信息。建立对象集X={x1,x2,…,xm}和属性集Y={y1,y2,…,yn}，并根据对象集和属性集建立关系矩阵A。

A=(aij)m×n

(1)

由于各指标属性不同、量纲不一，无法直接比较，所以应对关系矩阵A进行规范化处理。

根据辐射源威胁评估过程中，各属性变化对辐射源威胁程度的影响，分为效益型属性和成本型属性，分别进行规范化处理。

1)效益型属性：

(2)

2)成本型属性：

(3)

整合后得到评估矩阵B。

B=(bij)m×n

(4)

Step2确定各辐射源参数的权重，建立权重向量为W=[ωj]n=[ω1,ω2,…,ωn]，根据权重矩阵更新评估矩阵得到B′。

(5)

Step3根据更新后的评估矩阵B′计算模型的正理想解B+和负理想解B-。

(6)

(7)

(8)

1.2 基于CV-G1法赋权的权重向量计算

G1法以主观排序和指标间重要程度比较为关键，确定各指标权重。变异系数是反映各指标内部数据差异程度的统计量，变异系数越大反映该指标的变化越大，可能带来更多风险，因此可按照指标变异系数分配权重。

变异系数法相较于文献[18]中采用的熵权法，其一，可以在不对数据归一化处理的前提下，消除数据量纲不同的影响，节约计算时间；其二，受异常数据影响敏感度更低，不易产生相差过大且不符合实际的客观权重。

CV-G1法针对传统G1法赋值随意性强的缺陷，通过将各相邻指标差异系数比替代传统G1法中主观赋权，使属性权值在尽可能满足评价者要求的基础上，反映客观规律，减少主观赋权造成的数据模糊和偏差。具体计算步骤如下:

Step1根据专家系统，确定各属性指标重要性，由高到低排序。

Step2计算各属性变异系数：

(9)

其中：

(10)

(11)

Cj表示C是第j个属性的变异系数。

Step3将数据转换到按照重要性的排列方式，计算各相邻属性重要程度比：

(12)

Step4计算各项属性权重：

排序中第n重要属性权重：

(13)

其他属性权重由以式(14)递推得到：

ωn-1=rnωn

(14)

将得到权重按照原始数据属性排列顺序排序，得到权重向量W=[ωj]n=[ω1,ω2,…,ωn]。

2 基于IOWA算子的空值估算法

为保证辐射源威胁评估的准确性，针对实际评估过程中可能存在的数据缺失问题，引入基于IOWA算子的空值估算法补全丢失数据。本算法不仅考虑到不同属性之间的相关性，而且考虑到同一属性不同对象间数据的联系。对比IOWA算法估算得到的完备信息系统与真实完备信息系统，其协方差矩阵和均值向量差异较小，估值稳定可靠。

若信息系统部分数据缺失，则用特殊符号“*”表示该系统中缺失的数据(空值)。

定义2[17]一个IOWA算子是一个映射：

F:Rn→R

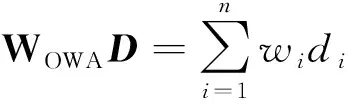
(15)

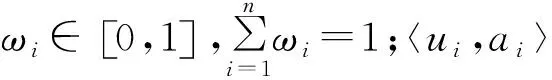
Pearson相关系数是表示2个变量X,Y之间线性相关程度，是用变量X,Y的协方差除以变量X,Y标准差的乘积：

(16)

算法具体步骤如下：

Step1假设关系矩阵A(包含m个辐射源x1,x2,…,xm、n个数据属性y1,y2,…,yn)中存在空值。仅考虑2种属性参数都存在的情况，剔除存在空值的辐射源数据重新排列。假设有k个2种属性参数齐全的辐射源，则计算得到属性ys与yt的Pearson相关系数r：

(17)

其中：

(18)

式中：|rst|表示两属性间相关程度，|rst|越大，则相关程度越高。所以，属性yi的相关属性为yj：

R(yi)=

{yj|rij≥riu,u≠j≠i,1≤i,j,u≤n}

(19)

根据上述方法，找出每个属性的相关属性。

Step2选择待填补属性yi和其相关属性yj数据均非空值的辐射源xh，将这2个值组成一个OWA对〈ahj,ahi〉，其中相关属性ahj值为序诱导变量，待填补属性ahi值为聚合变量。

将OWA对根据序诱导变量由大至小排序，若有OWA对的序诱导变量相等，则将其聚合变量取均值。得到排列后的聚合变量d1,d2,…,dnOWA。其中nOWA为OWA对的数量。

Step3基于模糊语言量化函数[17]，计算各OWA对权重。

(20)

表1 模糊语言的量化规则和参数值之间的关系

权重WOWA=[ω1,ω2,…,ωn]计算：

(21)

Step4根据IOWA算子聚合OWA对，得到：

(22)

Step5若系统信息已完备，则算法停止。

在以上算法中，每次迭代仅产生待填补属性的一个缺失值，且填补前其相关属性值保持不变。若待填补属性不满足上述条件，需再次计算各属性间的相关系数，并再次确定相关属性。

3 缺失数据下基于IOWA-TOPSIS的辐射源威胁评估流程

将TOPSIS评估算法和基于IOWA算子的空值估算法相结合，在数据缺失情况下对辐射源威胁评估排序，处理流程如图1所示：

Step 1基于辐射源与属性参数的关系矩阵A，通过计算存在缺失数据的属性与其他属性的Pearson相关系数，确定相关属性。并基于缺失数据属性与相关属性，构建OWA对。

Step 2按照序诱导变量对OWA对排列处理。首先，利用模糊语言量化函数构建OWA对的权重计算函数，并求解各OWA对权重，排序得到聚合变量。然后，使用IOWA算子聚合计算填补值，补全系统信息，得到关系矩阵A′。

Step 3规范化处理A′，得到评估矩阵B。基于B计算各属性变异系数，利用CV-G1法分配属性权重。

Step 4结合权重向量W与评估矩阵B，基于更新后的评估矩阵B′生成模型的正理想解B+和负理想解B-。

4 仿真分析

基于提出的IOWA-TOPSIS的辐射源威胁评估模型对各辐射源目标进行威胁评估：首先，对CV-G1赋权法效果进行评估；其次，在数据集不完备条件下，填补空值后进行评估，验证IOWA算子的有效性。

我方雷达和无源侦察设备探测到x1～x55个对方雷达辐射源，包含y1～y66种辐射源属性，得到各指标参数见表2。表2中，y1为速度，y2为距离,y3为达到位角，y4为载频，y5为重频，y6为脉宽。

表2 辐射源指标参数

根据1.1节Step1并结合表2中的数据得到评估矩阵B。

B=

(23)

经咨询该领域专家意见，确定辐射源指标属性重要性排序：y5>y4>y6>y2>y3>y1。并根据1.2节计算得到属性组合权重向量：

W=

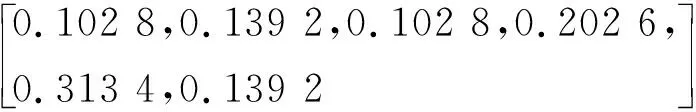
(24)

根据式(5)，用各属性权重更新评估矩阵，并根据式(6)计算模型的正理想解B+和负理想解B-：

(25)

根据式(8)、(9)计算得到各辐射源对正理想解的相对贴近度：

(26)

由此可得到5个辐射源威胁排序结果为x5>x1>x2>x3>x4。基于原始数据对辐射源分析：辐射源x5的载频较高，且具有较大重频、脉冲宽度较窄，能量集中，测量精度高，可对我方进行连续快速扫描，另外，其到达方位角小、距离短、接近速度快，对我方威胁程度最大；辐射源x1与x5相似，但相对接近速度较慢，威胁程度仅次于x1；辐射源x2、x3、x4重频相对x1和x5明显更小，对我威胁程度稍低，其中x2到达方位角和距离均小于x3、x4，在三者中威胁程度较高；x4脉宽明显大于其他辐射源，扫描精度低，故对我威胁程度最低。综上，分析得到的辐射源威胁程度大小关系与算法排序结果x5>x1>x2>x3>x4吻合。

利用表2数据分别在基于熵权法和CRITIC两种纯客观赋权方法的辐射源威胁评估模型中进行评估，对比3组相对贴近度结果见表3。

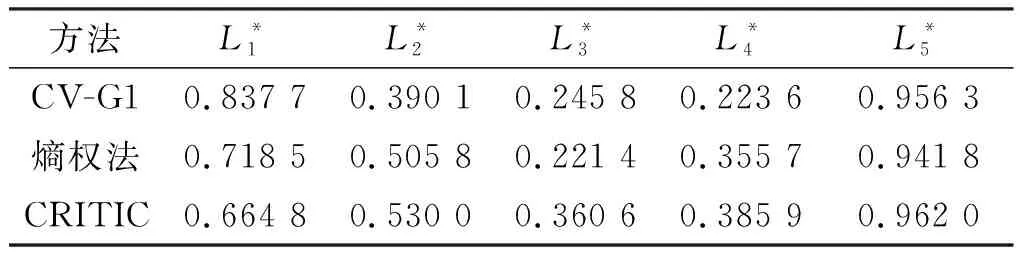
表3 辐射源相对贴近度(Ⅰ)

CV-G1赋权法与其他2种方法得到威胁程度排序结果相同，进一步验证了CV-G1赋权法与TOPSIS法结合算法的有效性。此外，辐射源x1威胁程度排序较高，但另外2种方法得到x1相对贴近度却与x5差距较大，这是由于客观赋权方法只考虑数据间差异性蕴含的信息量，忽略了实际使用中各属性对评估结果造成影响的价值。例如属性“重频”的数值间大小相差一般较大，根据熵权法和CRITIC等客观赋权方法认定其包含信息量较少，权重分别赋予较低的0.131 1和0.210 4，但重频却是辐射源威胁评估中需要首要考虑的指标，因此辐射源威胁评估数据的特点容易对客观评价标准造成扰乱，融入主观赋权因素可以使赋权结果更贴合实际。

CV-G1赋权法融入考虑主观因素的先验知识，保证评估结果与实际情况间的偏差更小，同时对数据中客观信息的充分利用提升了评估结果的准确性和可靠性。

验证CV-G1赋权法的有效性后，基于IOWA-TOPSIS算法在数据集不完备的情况下对辐射源进行威胁评估。不完备的辐射源指标参数见表4，根据第2节IOWA空值估计算法填补空值，得到补全信息的数据集见表5。

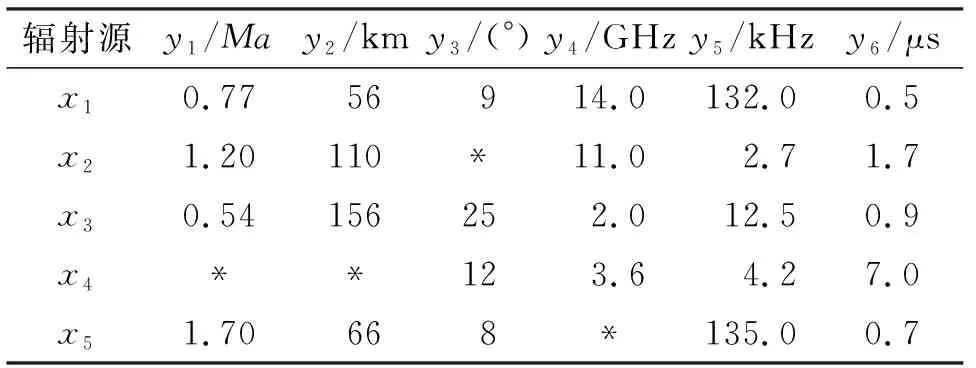
表4 不完备的辐射源指标参数

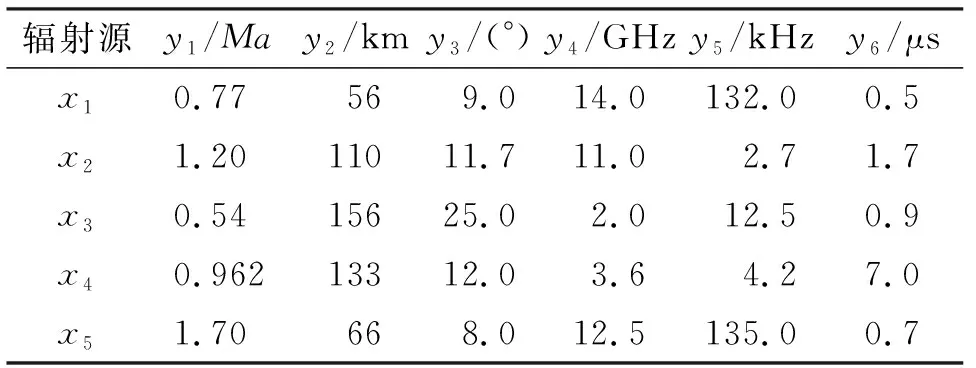
表5 补全的辐射源指标参数

根据1节TOPSIS法计算辐射源相对贴近度：

(27)

辐射源威胁排序结果为x5>x1>x2>x3>x4，与数据完备条件下评估结果相同。利用IOWA算子对缺失数据进行赋值，辐射源x1～x5相对贴近度大小相对于真实数据评估结果分别变化0.007 0、0.010 3、0.001 2、0.036 8、0.020 2，对辐射源威胁评估结果影响较小：一方面，IOWA算子赋值与真实值相近；另一方面，不影响未赋值属性变异系数，对各属性在TOPSIS中赋值影响较小。该评估模型客观还原了事实情况，能对辐射源信息系统中缺失数据进行合理填充。

此外，Mean Completer(MC)估算法是常见的空值填补方法，与IOWA算子同样具有处理速度快的特点，将其与辐射源威胁评估模型结合，得到辐射源贴近度如表 6 ：

表6 辐射源相对贴近度(Ⅱ)

相较于MC估算法，IOWA算子处理空值并得到的辐射源威胁评估结果误差较小，主要是因为MC算法不能深层次地挖掘信息系统包含的信息，导致估算效果不佳。而对比Combinatorial Completer、K-Nearest Neighbor、K-means Clustering等估算方法，IOWA算子又具有过程简单、计算速度快的显著优势。使用IOWA算子填补空值，可以利用数据间的关联性增大获得信息量，使空值填补结果更加贴近真实情况。IOWA算子适用于较小规模的空值估计，本次实验中空值率达到13.3%，算法空值填补效果较好。

在实际使用中，由于算法从采集数据间的相关性中提取信息，作为填补空缺数据的依据，在此过程中没有考虑辐射源各属性的公式关系和大小影响，不需要专业方面的先验知识，因此数据缺失的类别对该算法影响较小。当多种属性同时缺失或大量数据同时缺失时，由于数据中有关属性关联度的信息量大量减少，算法的估算精度会受到影响，通过多次选取不同数仿真发现，当数据缺失比大于17%时，算法稳定性下降，评估后出现不同结果，因此该算法适用于少量数据缺失的情况。

5 结论

1)引入IOWA算子改进TOPSIS评估模型，相比其他估值方法，IOWA基于数据属性间的关联预测缺失数据，对空值的估计更准确，保证了系统信息量的完整性。本文算法在保证计算速度的同时，拓展了TOPSIS的使用范围，有效解决了数据缺失条件下传统辐射源威胁评估方法无法有效工作的问题。

2)CV-G1赋权法通过融合基于先验知识的主观意见和基于数据特点的客观特征进行赋权，处理过程中，对主观因素的影响范围进行了限定，使用变异系数法量化各属性重要程度，为最终权值分配提供了客观依据，比仅考虑单方面因素的赋权法更准确。