基于特征增强的非均匀采样SAR三维稀疏成像

孙 豆, 邢世其，*, 高海峰, 庞 礴, 李永祯, 王雪松

(1.国防科技大学电子科学学院电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073;2.陕西省地质调查院, 陕西 西安 710054)

0 引 言

在合成孔径雷达(synthetic aperture radar,SAR)技术的发展中,很多研究工作致力于获取飞机、车辆等人造目标高分辨率的三维成像结果[1-2]。通常情况下,通过层析SAR[3-4]或全息SAR[5-6]获取三维波数域空间中的均匀密集采样可以得到高分辨率的三维成像结果。然而,这种数据采集方式耗时长且成本较高[7-8]。此外,在军事监察等多种领域中,获取均匀且密集的采样是不切实际的。作为一种新兴技术,非均匀采样SAR为获取高分辨率的三维成像结果带来了极大的方便[9-11]。通过多架搭载SAR系统的小型无人机(unmanned aerial vehicle,UAV)协同的非线性飞行[12-14]获取SAR数据是一种收集三维非均匀采样的可行方法。由于采集的数据稀疏且无人机平台具有良好的机动性,这种非均匀采样方式不仅高效并且大大节省了成本,适用于军事侦察等实际应用中。

非均匀采样的三维成像与均匀且密集采样的三维成像有很大的不同,传统的基于线性滤波的三维成像方法[5,15-16]并不适用。具体地说,非均匀采样使得俯仰向和方位向之间高度耦合,因此不能先二维成像,再估计高度信息,三维分步成像[4-5,17]不再适用。此外,由于非均匀采样是稀疏的,使用基于傅里叶变换的成像方法得到的成像结果会存在很强旁瓣,成像质量差[18-19]。作为一种模型匹配类方法,稀疏重构通过正则化约束可以得到稀疏的结果[20-21]。因此,结合稀疏重构进行三维成像有望得到三维高分辨成像结果。然而,三维稀疏成像面临巨大的计算压力,使重构具有很大挑战性和难度[22-23]。Austin提出了一种基于数据插值和快速傅里叶变换相结合的稀疏成像方法[7],解决了计算规模大的困难,使得非均匀采样的稀疏成像成为可能。但该方法中使用局部信息进行数据插值会产生较大的数据网格误差,进而影响成像结果的精度。此外,基于理想点散射模型的稀疏成像虽然可以得到稀疏的成像结果[24-25],但对于分布式目标,断裂开的稀疏的点并不符合其散射连续的本质,分布式目标的成像结果稀疏不利于后续的图像解译和目标识别。基于属性散射模型的稀疏重建[26-27]同时估计目标的尺寸、姿态、位置和散射幅度等多个参数,可以得到符合分布式目标散射本质的重建结果。然而,这类方法的计算复杂度很高,并且由于待估参数多,数据耦合严重,较难得到全局最优解。

为了充分利用非均匀采样数据,得到高质量的成像结果,本文提出一种基于特征增强的非均匀采样SAR三维稀疏成像方法。首先,基于无数据插值的非均匀数据,将成像问题直接建模为三维空间中联合的稀疏重构问题。在此模型基础上,选取候选散射中心进行字典降维和模型降维。之后,通过建立散射中心之间的三维联系,在模型中增加三维特征增强约束项,得到最终的三维稀疏重建模型。最后,结合高斯迭代法和优化的信号处理技巧,提出了一种高效的模型求解算法。通过仿真实验验证了该成像方法的有效性。与其他成像方法相比,本文所提方法具有以下优势:避免了局部插值带来的数据误差,因此成像精度高;增加了特征增强约束项,因此保证了分布式目标成像结果的连续性;通过字典降维和信号处理技巧减小了计算规模,因此在提高成像质量的同时保证了计算效率和现有方法相当。

1 信号模型

相对于场景中心,雷达的方位角为φ,俯仰角为θ,并发射宽带信号。假设雷达距离场景足够远,使用平面波模型,接收的信号可以表示为

(1)

式中,t表示时间;c是光速;s(t)是中心频率为fc且带宽为BW的已知宽带信号;*表示卷积。场景的反射率函数由g(x,y,z;φ,θ)表示,x,y,z为目标在场景中的位置。

式(1)可以理解为投影到x维的场景反射率函数的傅里叶变换。根据投影切片定理,反射率函数满足

(2)

式中,G(kx,ky,kz)表示由接收信号r(t;φ,θ)和宽带信号s(t)得到的波数域观测信号。

波数域观测的每个支撑集是波数域采样点(kx,ky,kz)上的一个线段。以4πfc/c rad/m为中心,以雷达观测角度(θ,φ)为方向的波数域采样点表示为

(3)

式中,频率f的采样为f→fj,观测角度的采样为(θ,φ)→(θq,φq)。

本文的任务是根据式(2)中给出的已知波数据观测和反射率函数之间的关系,对反射率函数进行估计。图1给出了5架无人机协同飞行的雷达扫描轨迹,由一组随机曲线组成。可以看出这种非均匀采样方式形成了复杂的基线。图2给出了图1轨迹对应的波数域采样情况,可以看出由观测角度(即扫描轨迹)确定的波数域采样是非均匀且稀疏的,这就使得成像难度变大。为了获得非均匀且稀疏的波数域采样的三维高分辨成像结果,下面将稀疏重构与非均匀采样的数据特性相结合,进行稀疏成像建模。

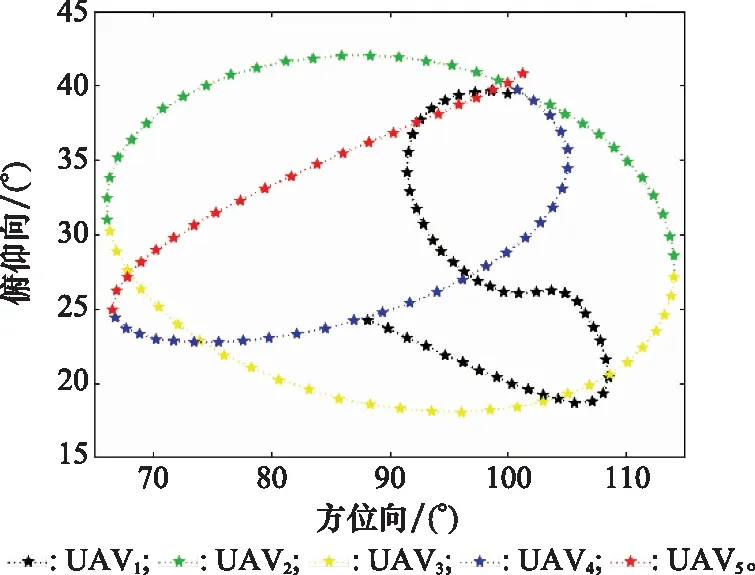
图1 UAV协同飞行的扫描轨迹

图2 UAV协同飞行的波数据采样

2 稀疏成像建模

一般情况下,SAR图像的场景是稀疏的,特别是对于人造目标而言,其由少量的强散射体组成[17]。考虑到场景的稀疏性,将成像问题建模为稀疏重构问题有望提高成像结果的质量。为了高效率地得到高分辨率高质量的成像结果,下面分3步进行稀疏成像建模。

首先建立直接三维稀疏成像模型,避免将非均匀数据插值为均匀数据带来的误差。之后,进行模型降维处理,解决直接三维稀疏成像模型求解中面临的计算量大、存储压力大的问题。为了保证分布式目标成像结果连续,最后在模型中增加三维特征增强约束项。

2.1 直接三维稀疏成像模型

在图像重构空间中,我们定义一组N个候选散射中心的位置:

(4)

通常,这些位置从均匀的矩形网格中选择。基于这些位置和波数域采样,M×N维的字典矩阵表示为

A=[e-j(kx,mxn+ky,myn+kz,mzn)]m,n

(5)

式中,m=jq表示波数域中M个观测的索引;n表示C中N个候选散射中心的索引。

为了避免数据插值带来的误差,这里直接利用式(5)中的字典矩阵建立直接三维稀疏成像模型。

结合式(5),将式(2)写成矩阵形式,得到

b=Aβ

(6)

式中,向量β是要重建的三维图像;向量b是M维的波数域观测。

三维稀疏成像等价于解决下面的稀疏重构问题:

(7)

式(7)中的数学模型不是一个凸优化问题,而是一个NP难问题。由于lp范数具有产生稀疏和更精确的解的能力,且非常类似于l0范数[28],这里使用lp范数将式(7)中的模型松弛为下面的优化问题:

(8)

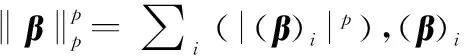
2.2 模型降维

在观测场景中,我们感兴趣的只是目标区域。并且通常情况下,目标区域以外的大部分区域的成像结果强度都很小甚至为零,特别是由强孤立散射体组成的目标。因此,只需对目标区域进行成像,进而获取目标的成像结果。基于此,下面通过选取候选散射中心进行字典降维,同时降低稀疏成像模型的规模。

(9)

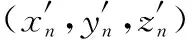
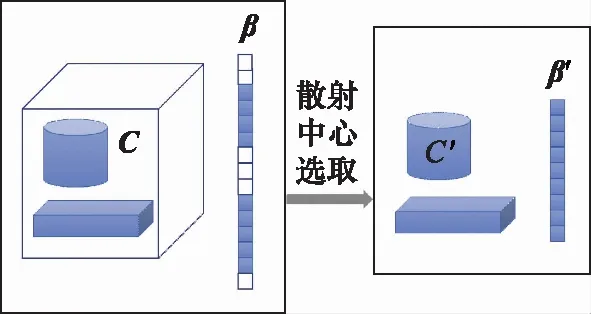
图3 散射中心选取示意图

(10)

候选散射中心选取后,字典矩阵更新为

(11)

由于选取后的候选散射中心数目为N1,字典矩阵A′的维数降为M×N1。同时,稀疏成像模型更新为

(12)

经过散射中心选取,式(12)中模型的规模相比于式(8)缩小了很多,计算量和存储压力也随之变小。

2.3 三维特征增强

稀疏成像使用式(2)所示的点散射模型,成像结果通常是由几个稀疏的点组成的。实际上,分布式目标的电磁散射模型并不是简单的点散射模型。因此,在对分布式目标稀疏成像时,其成像结果会出现断裂的情况,由一些断裂开的点组成。这样的成像结果不利于后续的目标识别和图像解译。

为了同时保持稀疏成像对于旁瓣的有效抑制和对点散射目标的高分辨成像,并增强分布式目标,得到分布式目标连续且平滑的成像结果,我们给稀疏成像模型中增加三维特征增强约束项,即通过建立相邻散射中心散射强度之间的关联,约束能量分布趋于均匀。模型改进为

(13)

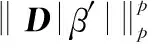
在三维空间中,目标散射中心的相邻散射中心有13个,分别位于直角坐标系的3个方向上和斜对角线的10个方向上。通过仿真发现,选取直角坐标系的3个方向上的相邻散射中心足够实现区域的平滑,因此三维特征增强只对这3个方向进行约束,D矩阵表示为

(14)

三维特征增强约束项表示为

(15)

式中,Dx|β′|,Dy|β′|,Dz|β′|表示每个目标散射中心与图4所示的x,y,z3个方向上的相邻散射中心之间的强度变化情况。对于选取后的候选散射中心β′内某一序号为q的目标散射中心,其在x,y,z3个方向上的前向相邻散射中心的序号分别为qx,qy,qz,如图4所示。基于此,则Dx,Dy,Dz为

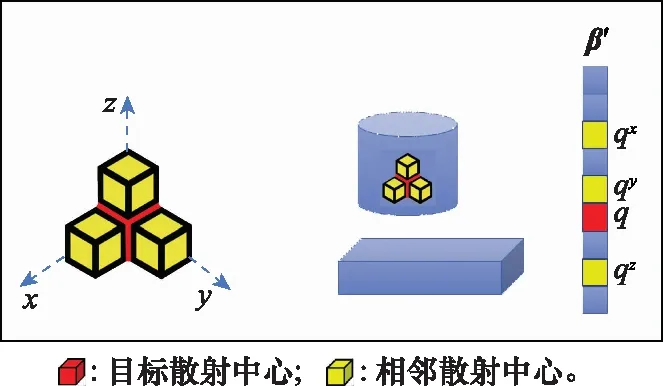
图4 三维特征增强示意图

Dx=Λ+X,Dy=Λ+Y,Dz=Λ+Z

(16)

式中,

Λ=diag(-1)

(17)

(18)

三维特征增强项建立了相邻散射中心幅度变化的约束。通过调整正则化参数λ2,可以约束相邻散射中心之间幅度变化程度,达到对分布式目标成像结果进行增强的目的。

3 稀疏成像算法

经过上面的推导,最终要求解的模型为式(13)。根据式(13),定义代价函数J(β′):

(19)

当代价函数J(β′)取最小值时,就得到了稀疏重构的结果。受Cetin的处理思想[29]启发,首先计算J(β′)对β′的偏导:

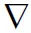
(20)

式中,Λ1(β′)=diag(|(β′)i|p-2)是N1维的对角矩阵,H(β′)为

H(β′)=ΦH(β′)DxHΛx(β′)DxΦ(β′)+

ΦH(β′)DyHΛy(β′)DyΦ(β′)+ΦH(β′)DzHΛz(β′)DzΦ(β′)

(21)

式中,

Λx(β′)=diag(|(Dx|β′|)i|p-2)

(22)

Λy(β′)=diag(|(Dy|β′|)i|p-2)

(23)

Λz(β′)=diag(|(Dz|β′|)i|p-2)

(24)

Φ(β′)=diag(exp(-jφ[(β′)i]))

(25)

式中,φ[(β′)i]表示(β′)i的相位。

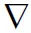
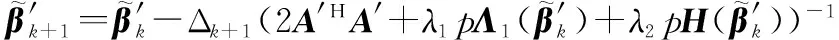
(26)

(27)

(28)

实际上,式(27)的计算规模很大。为了降低计算量和存储压力,进而高效地进行迭代计算,这里采用一种优化的信号处理技巧。

算法1总结了所提出的稀疏成像算法的具体步骤。

算法1 基于特征增强的非均匀采样SAR三维稀疏成像算法1.使用3D-NUFFT进行成像,得到初始成像结果β⌒;2.根据式(9)和初始成像结果β⌒,确定目标区域C′;3.根据目标区域C′以及序号为q的目标散射中心在x,y,z3个方向上的前向相邻散射中心的序号qx,qy,qz,确定Dx,Dy,Dz;4.根据目标区域C′、波数域观测G(kx,ky,kz)和波数域采样kj,qx,kj,qy,kj,qz,计算并存储A′Hb和A′HA′;5.根据式(27)迭代计算β～′k+1,当‖β～′k+1-β～′k‖22/‖β～′k‖22<τ时,得到解β～′=β～′k+1;6.根据式(28),由β～′拼接得到完整的三维成像结果β～。

4 仿真实验与分析

为了评价本文提出成像方法的性能,本节基于电磁仿真数据开展仿真实验,并将本文方法和3D-NUFFT,Austin方法进行对比。实验在一台配备Intel Core I5-6 500 CPU和12 GB RAM的计算机上的Matlab R2016b上进行。

4.1 成像性能分析

选取单个三面角作为仿真目标,从抗噪性、采样分布依赖性、成像结果分辨率、计算时间这4个方面分析本文成像方法的性能。回波数据由电磁仿真软件生成,雷达中心频率为10 GHz,带宽为2 GHz,三面角放置在场景中心。

图5给出了3种不同采样方式沿俯仰角和方位角的扫描轨迹。三面角的散射回波数据依据这3种采样方式获取。虽然3种扫描轨迹不同,但这3个轨迹的方位角和俯仰角范围分别都是[86°,96°]和[18°,42°]。因此,比较它们的成像结果是合理的。这3种不同采样方式的波数据采样情况如图6所示。可以看出每种采样方式的波数域采样都是非均匀且稀疏的,但波数域采样的分布情况各不相同,方式1是最稀疏的,方式3最密集。

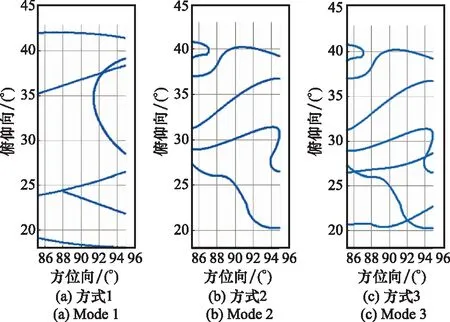
图5 3种采样方式的扫描轨迹

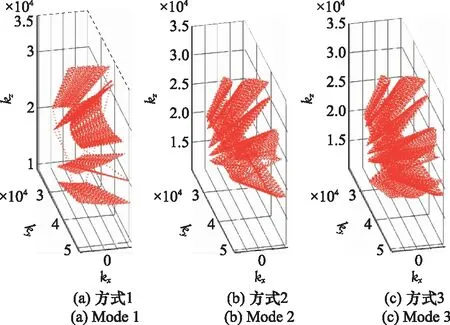
图6 3种采样方式的波数据采样

依据图5中3种采样方式下的回波数据,使用本文方法、3D-NUFFT和Austin方法对三面角进行成像得到如图7所示的结果。图7中,设置显示成像结果的幅度阈值为-20 dB,每个子图的中间青色部分是目标的三维成像结果,周围灰色部分是X-Y、Y-Z和X-Z方向的二维投影结果。从图7可以看出,不同采样方式下的3D-NUFFT成像结果存在差异,且均不理想,旁瓣很高。而对于Austin方法和本文方法,每种采样方式下的成像结果相似,都只有一个椭球,完全去除了多余的旁瓣,实现了单个三面角的稀疏三维成像,且这两种方法不受采样方式的影响,采样分布依赖性低。为了更直观地对比这3种方法,图8给出了成像结果在距离向、方位向和俯仰向的切片图。从图中可以看出,每种采样方式下,3D-NUFFT方法得到的结果的主瓣最宽,且明显可以看见旁瓣。因此,该方法分辨率差,并且旁瓣抑制能力差。对于Austin方法和本文方法,其结果均具有显著的稀疏特性,主瓣较窄,并且都抑制掉了旁瓣,两种方法具有一定的旁瓣抑制能力。然而,相比较于Austin方法,本文方法结果的主瓣更窄,因此具有更好的分辨率。

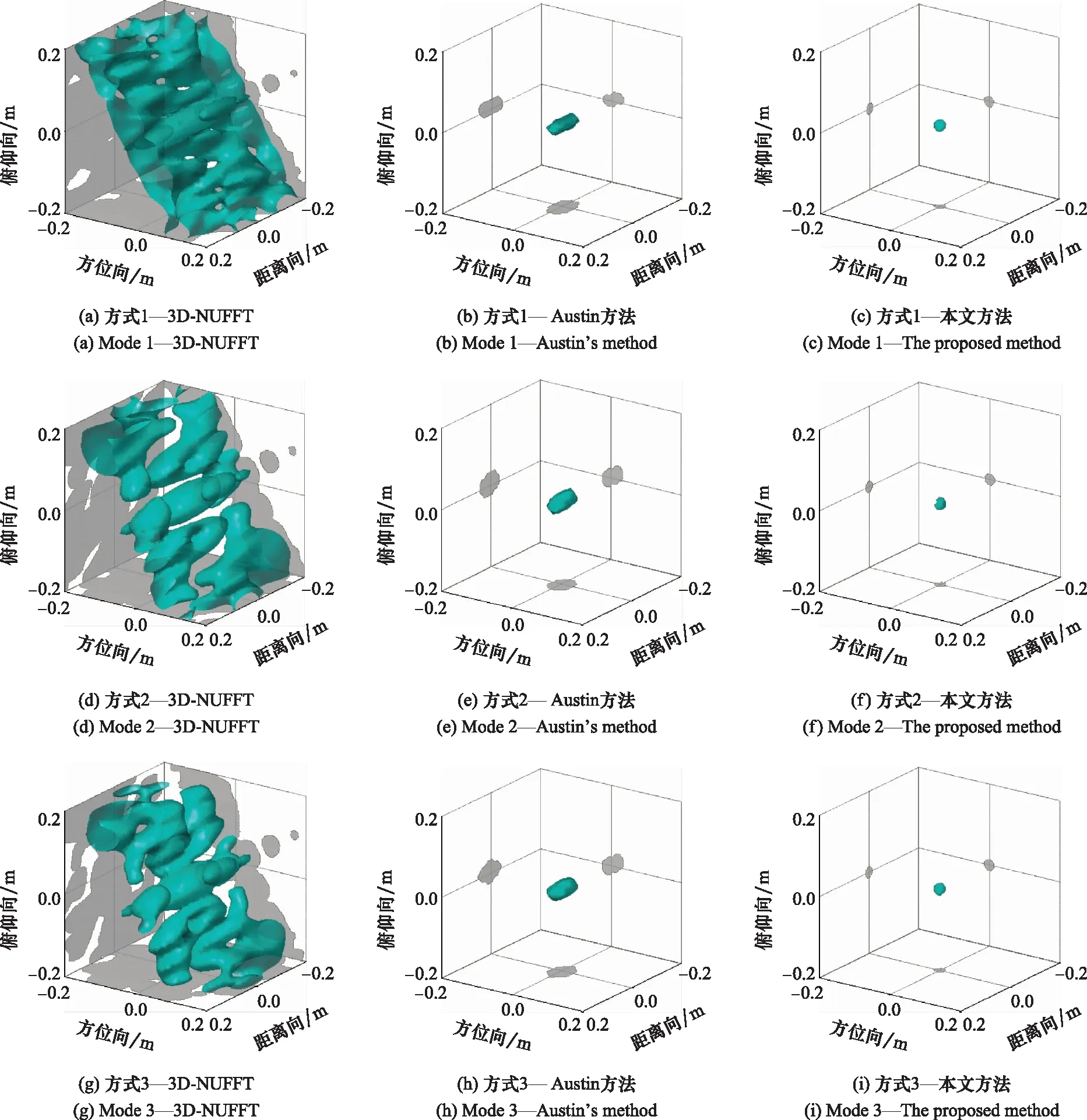
图7 三面角的成像结果

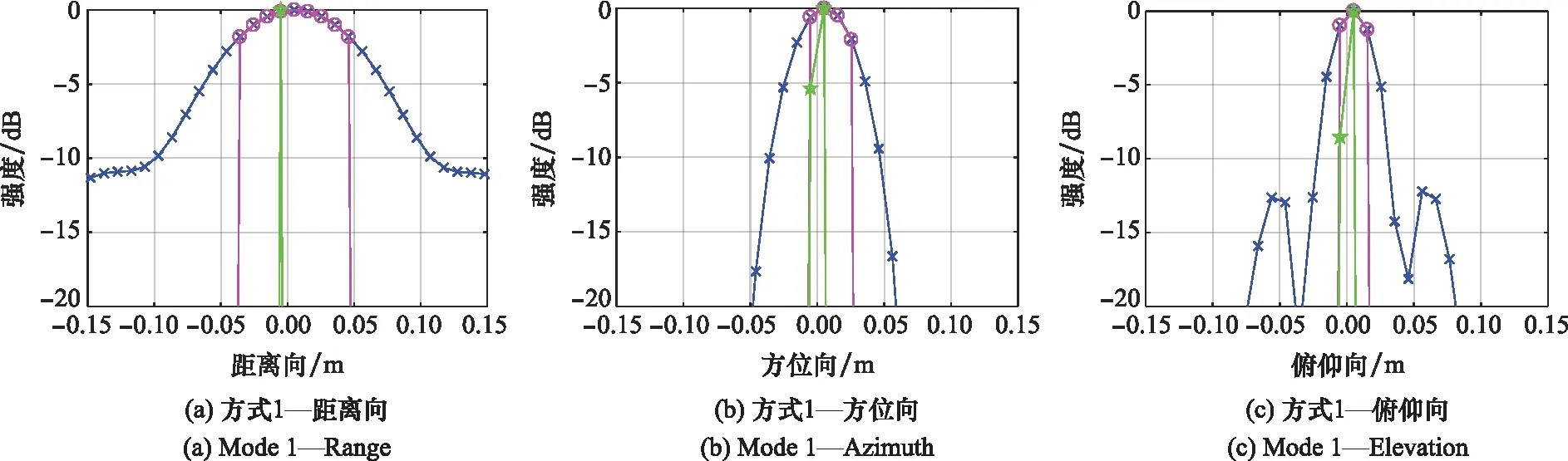
图8 三面角成像结果的切片图

图9给出了不同轨迹和不同信噪比下本文方法和Austin方法的成像结果分辨率对比结果。这里参考文献[30]中对分辨率的定义,取三维成像结果中大于-6 dB的椭球体积作为成像分辨率值。由于 3D-NUFFT的成像结果较差,这里没有选取此方法进行对比分析。从-40 dB到10 dB,在不同的SNR下进行了50次试验。从图9可以看出,当信噪比大于-30 dB时,所有曲线趋于稳定,分辨率值基本保持不变,且本文方法的分辨率总是优于Austin方法。此外,不同采样方式下本文方法的分辨率值基本相同,而Austin方法在3种采样方式下的分辨率值略有不同。当信噪比小于-30 dB时,随着信噪比的降低,所有曲线都开始上升,两种方法的成像质量越来越差。

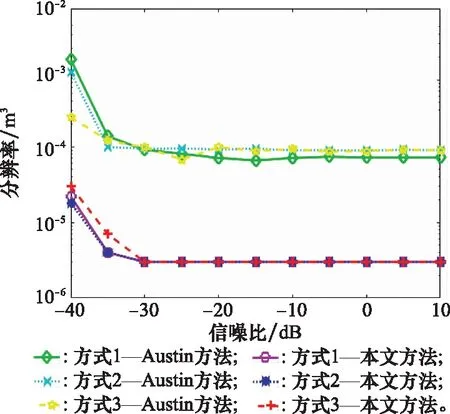
图9 分辨率对比结果

根据以上结果可得,Austin方法和本文方法基本上具有相同的抗噪性能,且均不受采样方式的影响,对采样分布的依赖性低,但是在成像结果分辨率上,本文方法优于Austin方法。

表1给出了3D-NUFFT、Austin和本文方法计算时间的对比结果。可以看出,3种不同方法的计算时间差距不大,计算效率基本处于一个水平。3D-NUFFT所需的计算时间最少,而Austin方法由于包含了3D-NUFFT中的插值步骤,所需的时间比3D-NUFFT略多。本文方法直接对非均匀数据进行稀疏重构,因此相比于Austin方法,算法的收敛需要更多的时间。

表1 不同成像方法的计算时间比较

4.2 典型目标成像结果

为进一步验证本文成像方法的有效性,下面选取两个典型目标开展仿真实验,并比较本文方法成像结果和其他成像方法的不同。

为了对比本文方法和其他方法在成像结果精度上的差异,首先对一个飞机目标进行仿真实验。图10给出了飞机的三维CAD模型,由13个三面角组成。

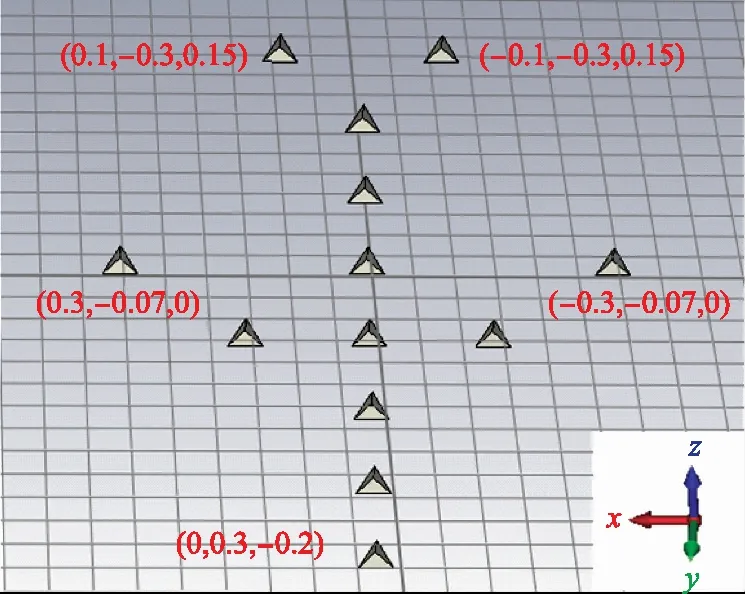
图10 飞机的三维CAD模型

飞机的长度和宽度分别为0.7 m和0.6 m,在场景中的倾角为30°,因此成像场景的高度为0.35 m。回波数据由电磁仿真软件生成,雷达中心频率为10 GHz,带宽为2 GHz,雷达沿俯仰角和方位角的扫描轨迹与图5(a)所示的采样方式1一致。

图11给出了使用不同成像方法得到的飞机三维成像结果。

图11 飞机的成像结果

图11(a)中设置显示成像结果的幅度阈值为-10 dB,图11(b)和图11(c)中设置显示成像结果的幅度阈值为-20 dB。如图11(a)所示,由3D-NUFFT得到的成像结果质量较差,具有高的旁瓣,成像结果中看不到飞机的轮廓。图11(b)中Austin方法得到的成像结果可以看出飞机的大致轮廓,但是成像结果的质量一般。虽然Austin方法减少了大部分的旁瓣,但成像结果中仍有一些旁瓣没有被去掉,对旁瓣的抑制能力不够,图11(b)中用橙色圈出了这些旁瓣。此外,Austin方法成像结果的精度也一般,没有得到机翼上的两个三面角的成像结果,图11(b)中用红色圈出了这一缺失的部分。实际上,由于Austin方法中包含基于局部数据信息的插值步骤,数据插值带来的额外误差影响了成像效果,造成了图11(b)中成像结果精度不高。图11(c)给出了本文方法的成像结果,可以看出成像结果准确度很高,与真实场景吻合,飞机的轮廓非常清晰,旁瓣被完全去除掉了,且13个三面角在图11(c)中都被显示出来了。因为本文方法不需要数据插值,保证了数据的真实性,因此相比其他成像方法,本文方法不仅对旁瓣抑制能力强,并且获得的成像结果精度更高且更稀疏。

最后,为了测试本文方法对分布式目标的成像效果,这里使用Slicy模型进行仿真实验,图12给出了其三维CAD模型。Slicy模型由三面角、二面角、圆柱等组成,其中的二面角、圆柱是典型的分布式目标。回波数据由电磁仿真软件生成,雷达中心频率为10 GHz,带宽为2 GHz,雷达沿俯仰角和方位角的扫描轨迹与图5(a)所示的采样方式1一致。

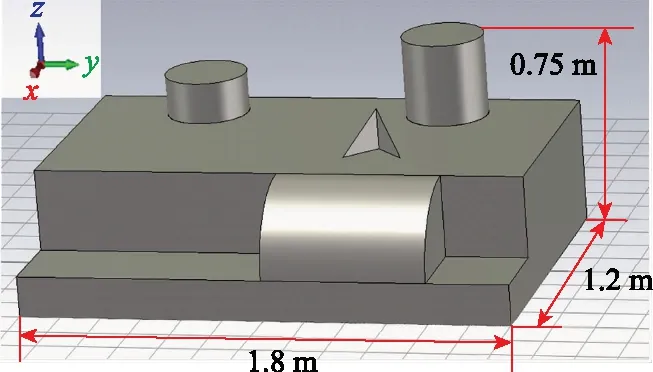
图12 Slicy的三维CAD模型

图13给出了使用不同成像方法得到的Slicy模型三维成像结果。为了验证本文方法对分布式目标成像的有效性,图13中还增加了本文方法在没有三维特征增强约束项时的成像结果进行对比。图13(a)中设置显示成像结果的幅度阈值为-10 dB,图13(b)～图13(d)中设置显示成像结果的幅度阈值为-20 dB。如图13(a)所示,通过3D-NUFFT获得的成像结果较差,并且具有很高的旁瓣。图13(b)中Austin方法去除了大部分旁瓣,但成像结果中仍有一些旁瓣没有被去掉,对旁瓣的抑制能力不够,图13(b)中用橙色圈出了这些旁瓣。此外,Austin方法的成像结果的精度较低,二面角的成像结果出现断裂的情况,且有些部分没有被重构出来,图13(b)中用红色圈出了这些部分。图13(c)给出了本文方法在没有三维特征增强约束项时的成像结果,该结果稀疏,完全去除掉了旁瓣,对旁瓣抑制能力强,并且Slicy模型每个部分都被重构出来了,但是图13(c)中用紫色圈出的分布式目标的成像结果是断裂的,由多个离散点组成,并不符合分布式目标连续散射的机理。本文方法的成像结果如图13(d)所示,由于增加了特征增强约束项,该结果不仅保持了稀疏成像对旁瓣的抑制,完全去除了旁瓣,并且得到了连续的分布式目标成像结果,避免了稀疏的点组成分布式目标的情况。图13(d)中Slicy模型的每个部分都被重构出来,和真实场景匹配且成像结果连续,这就验证了本文方法对分布式目标成像的有效性。

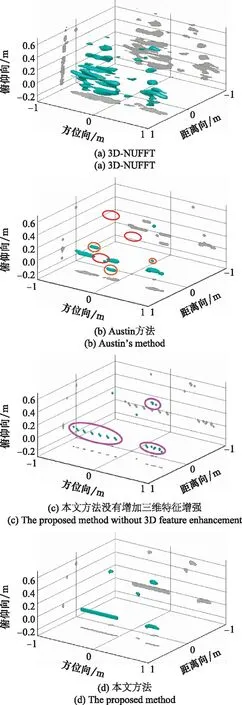
图13 Slicy的成像结果

5 结 论

本文提出了一种基于特征增强的非均匀采样SAR三维稀疏成像方法。该方法直接对非均匀采样数据进行稀疏成像建模,避免了局部插值对结果带来的不良影响,保证了数据的真实性。由于模型中增加了特征增强约束项,因此该方法不仅保持了稀疏成像对旁瓣的有效抑制,且保证了分布式目标成像结果连续。字典降维和信号处理技巧减小了计算规模,因此在提高成像质量的同时,该方法保证了算法计算效率和其他现有方法相当。从实验结果来看,本文方法在抗噪性、采样分布依赖性、计算效率这3个方面和其他方法的性能相当。在旁瓣抑制能力、成像结果分辨率和精度方面,本文方法明显优于其他方法,且本文方法可以得到分布式目标连续的稀疏成像结果。