基于模型转换频率估计的低空目标分类

陈唯实, 黄毅峰, 陈小龙, 卢贤锋, 张 洁

(1.中国民航科学技术研究院, 北京 100028; 2.海军航空大学, 山东 烟台 264001)

0 引 言

近年来,随着无人机产业的快速发展,世界各地无人机扰航事件频发[1]。无人机黑飞造成的安全隐患,为低空安全敲响了警钟,引发公众极大关注。以“无人机云”为代表的合作监视技术覆盖了绝大部分合法飞行的消费级无人机,因此少量自行组装的非合作无人机成为暴恐分子的作案工具,严重危害低空安防[2]。

目前,无线电侦测[3]、光电[4]、声学[5]、雷达[6]4类最为典型的非合作无人机目标探测技术各具优势和不足。其中,无线电侦测技术的优势在于能够快速定位无人机飞手,但其对于静默无人机的失效成为其最大短板。光电设备虽在一定距离内善于目标识别,但本身不具备测距功能,需要配备激光定位设备实现测距。近年来,随着神经网络和深度学习算法的发展,光学数据成为无人机分类识别中非常有价值的数据源,成为雷达数据的重要补充,利用卷积神经网络、快速区域卷积网络、反卷积网络等经典的深度学习模型开展无人机等低空目标识别分类,涌现出大量研究成果[7-10]。声学探测设备在嘈杂环境中的适用性较差,且探测距离有限,通常采用在较小范围内布设麦克风阵列的方法进行探测[11-14]。总的来说,虽然传统雷达尚未彻底解决低慢小目标探测问题,但其仍然是低空预警的主要技术手段。

一般情况下,飞鸟是雷达探测无人机目标过程中最大的干扰源。近年来,微多普勒(micro-Doppler, m-D)特征[15]作为目标自动分类中最常用的雷达精细化信号特征,已成为无人机雷达探测应用中一个非常活跃的研究方向[16]。Harmanny等[17]较早采用短时傅里叶变换(short time Fourier transform, STFT)提取m-D特征,通过提取旋翼数量、直径、叶尖速度等关键特征对旋翼无人机进行分类。Molchanov等[18]同样采用STFT提取m-D特征,并训练3个分类器对10类旋翼无人机和鸟类进行分类。在文献[19]中,分别采用STFT、倒频谱和节奏速度谱3种常用的信号表征方法生成m-D特征,进而通过训练支持向量机(support vector machine, SVM)分类器对实测的固定翼、旋翼无人机与飞鸟目标数据进行分类。Ren等[20]在m-D特征提取过程中利用相位谱信息,将二维正则化复对数傅里叶变换与降维技术相结合,实现了无人机和飞鸟目标分类。有研究者基于m-D标签对雷达回波信号进行分解,利用提取的8个几何与统计特征训练非线性SVM分类器,实现无人机目标类标签预测[21]。Ma等在文献[21]的基础上,将无人机目标特征与三类熵相融合,并将信号下采样与归一化特征输入非线性SVM分类器[22]。刘玉琪等[23]利用数字电视外辐射源雷达开展多旋翼无人机微多普勒效应实验,证实了外辐射源雷达提取无人机微动特征的可行性。

虽然目标m-D特征已成为无人机与飞鸟目标分类的主要技术手段,但此类方法要求雷达具有凝视目标并获取其精细化回波信息的能力。传统的监视雷达通常采用机械扫描天线,聚焦单个目标的时间很短,难以捕获m-D特征。因此,利用目标的雷达散射截面(radar cross section, RCS)等回波信号特征或轨迹特征对检测到的目标进行分类,成为适用于此类雷达的可能的技术途径[24]。Torvik等[25]利用监视雷达信号中提取的9个极化特征,采用最近邻分类器进行无人机与鸟类目标分类,同样获得了较高的分类精度。Messina等[26]利用监视雷达回波数据,建立了包含目标RCS、信噪比、速度、跟踪轨迹等信息的目标特征集,采用SVM分类器对无人机和飞鸟目标进行分类,取得了较好的分类效果。

针对上述问题,前期研究提出一种基于目标跟踪滤波的无人机目标识别方法,取得了一些初步成果[27]。在此基础上,本文进一步优化了算法流程,在完成目标跟踪滤波之后,通过轨迹平滑处理将前向和后向运行的两个多模型滤波器的估计值相结合,进一步扩大无人机与飞鸟目标的轨迹特征区分度,并在更为复杂的仿真与实测场景中验证了算法的有效性。

1 建模与分析

本节在给出算法流程的基础上,分别详述了目标跟踪、目标平滑和特征提取的方法和数据处理流程。

1.1 算法流程

算法分为以下步骤:目标跟踪、目标轨迹平滑、特征提取与分类,具体如图1所示。本文算法基于飞鸟目标的机动性高于轻小型无人机的假设,根据目标运动模型转换频率联合估计值区分飞鸟和无人机目标。

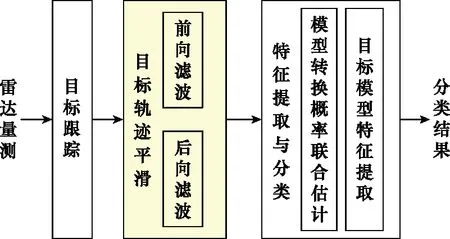
图1 无人机与飞鸟目标分类算法流程

1.2 目标跟踪

跟踪过程中的每一时刻,通过综合多个滤波器的状态估计配置模型初始值,进而基于交互式多模型[28]并行工作机制将所有滤波器生成的更新状态估计进行加权组合,权重根据每个模型的概率确定,在算法的滤波部分计算完成。

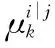
(1)

(2)

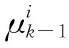
每个滤波器的均值和协方差分别为

(3)

(4)

对每个模型Mi,进行滤波处理:

(5)

(6)

式中,标准卡尔曼滤波的预估和更新由KFp(·)和KFu(·)表示。此外,针对每个滤波器,量测相似度为

(7)

每个模型Mi的概率计算为

(8)

(9)

式中,c是归一化因子。

计算状态均值和协方差的组合估计为

(10)

(11)

1.3 目标轨迹平滑

与单个模型的情况相同,可以基于所有的测量值平滑多模型滤波器的状态估计。因为n个模型K个测量值的最优固定区间平滑需要运行nK个平滑器,因此需要采用次优的方法。在完成目标跟踪之后,将前向运行和后向运行的两个多模型滤波器的估计相结合,能够在平滑轨迹的同时扩大不同轨迹特征的区分度。

首先讨论后向运行的多模型滤波方程,然后讨论将两种滤波估计进行组合的平滑方程。目标是计算每一时刻的后向滤波密度p(xk|yk:N),其表示为一组模型条件密度之和,即

(12)

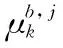
基于模型的后向滤波密度表示为

(13)

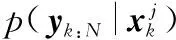
(14)

(15)

式中,aj为归一化常数,计算方式为

(16)

(17)

(18)

式中,bi为归一化常数,且

(19)

(20)

(21)

其混合预估均值和协方差分别为

(22)

(23)

(24)

每个模型的量测相似度计算为

(25)

(26)

式中,a为归一化常数,且

(27)

最后,总体后向滤波分布的高斯近似为

(28)

其均值和方差分别为

(29)

(30)

1.4 特征提取与目标分类

完成后向滤波之后,得到固定间隔平滑分布：

(31)

式中,平滑模型概率为

(32)

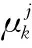
(33)

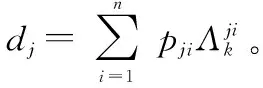
(34)

(35)

(36)

式(36)近似为

(37)

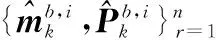
(38)

式中,

(39)

(40)

(41)

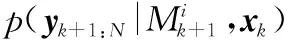
(42)

式中,

(43)

(44)

(45)

式中,

(46)

(47)

因此,可以匹配整体平滑分布的矩特征,给出单一的高斯近似：

(48)

式中，

(49)

(50)

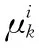
1.5 程序设计步骤描述

本节以伪代码的方式对目标跟踪、轨迹平滑和特征提取的过程进行描述,便于加深对雷达数据输入、输出以及飞鸟与无人机目标分类各个步骤中的数据处理方法的理解。在数据的处理过程中,输入为每个扫描周期的雷达量测,输出为目标轨迹的分类结果,详述如下:

2 仿真数据分析

2.1 仿真模型

本文采用两种模型对无人机和飞鸟目标运动轨迹进行仿真,包括匀速直线运动和机动变速运动[27]。图2所示为1个无人机和20个飞鸟目标运动轨迹的仿真示例,包括全局视图和局部放大图。

图2 低空多目标跟踪仿真

本文进一步提高了无人机与飞鸟目标飞行轨迹的复杂度,各项参数设置如下。

(1)无人机与飞鸟目标的轨迹均通过1 000次蒙特卡罗仿真实验生成。

(2)无人机目标采用匀速直线运动模型,起始点随机分布在空间[-100,100]×[-100,100]中。

(3)为提高无人机飞行轨迹的复杂度,其飞行轨迹经过两次变向,分为3个阶段,第1阶段步数为240,其起始速度为[2,-1];第2阶段步数为400,其起始速度为[-2,-2];第3阶段步数为300,其起始速度为[3,-1];共计940步。

(4)由于无人机目标仿真运动数据出现了高机动变向,因此每次变向后的跟踪过程可能会出现目标丢失和目标重新起始的现象。

(5)飞鸟目标采用匀速直线运动模型和机动变速运动模型的组合,其轨迹的起始位置随机分布在空间[-100,100]×[-100,100]中。

(6)每个飞鸟目标的跟踪步数在20～60之间随机设置,起始飞行方向随机生成。

(7)在切换概率P的控制下,飞鸟目标的运动模型在匀速直线运动模型和机动可变运动模型之间随机切换。

2.2 仿真结果分析

本节基于飞鸟与无人机目标轨迹的跟踪仿真数据,对算法优化前后的目标分类效果进行分析、对比和验证。

图3通过一次蒙特卡罗实验比较了无人机和飞鸟目标跟踪的均方根误差(root mean square error, RMSE),很明显,平滑算法通过将前向和后向运行的两个多模型滤波器的估计值相结合,显著降低了两个目标跟踪结果的RMSE。

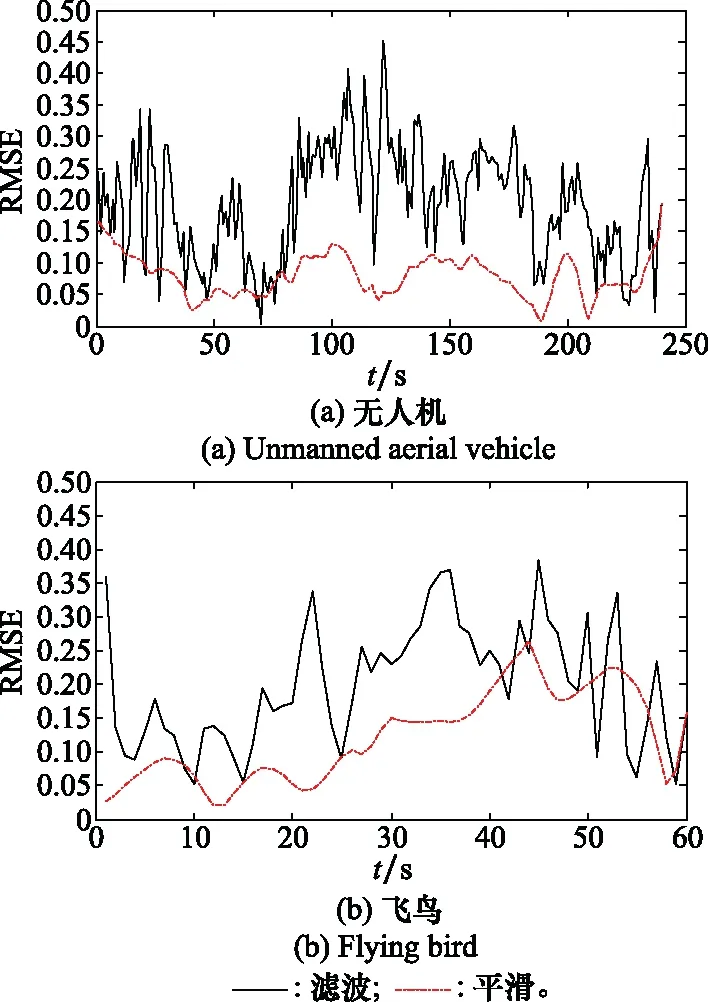
图3 目标跟踪结果的RMSE

表1提供了1 000次蒙特卡罗实验平均值的精确定量对比,其中NT代表跟踪步数。随着NT值的增加,无人机滤波结果的RMSE减小,而飞鸟滤波结果的RMSE增大。对于平滑后的结果,无人机和飞鸟的RMSE跟踪结果均随仿真步数的增加而减小。由于无人机的航迹更为平滑,其跟踪效果总体优于飞鸟。从数据比较可以看出,如果采用一般的滤波跟踪算法,对于飞鸟这样的高机动目标,仿真步骤越多,跟踪效果往往越差。对于平滑算法,更多的仿真步骤能够降低RMSE,提高对飞鸟和无人机等不同机动目标的跟踪效果。

表1 1 000次蒙特卡罗实验获取的仿真目标跟踪RMSE

图4和图5分别对比了无人机和飞鸟目标在某次跟踪仿真中的滤波与平滑估计的模型概率结果,其中飞鸟目标的模型切换频率为P=0.3。在无人机目标的跟踪仿真中,模型1和模型2的滤波估计概率分别约为0.8和0.2,而平滑估计概率接近于1和0,可见其只选择了一种模型,未进行模型切换。同样选择60步跟踪仿真结果进行对比,飞鸟目标在2个模型之间切换5次,2个模型的滤波与平滑估计概率都有较大波动,明显高于无人机目标,利用该特性可以区分两类目标。

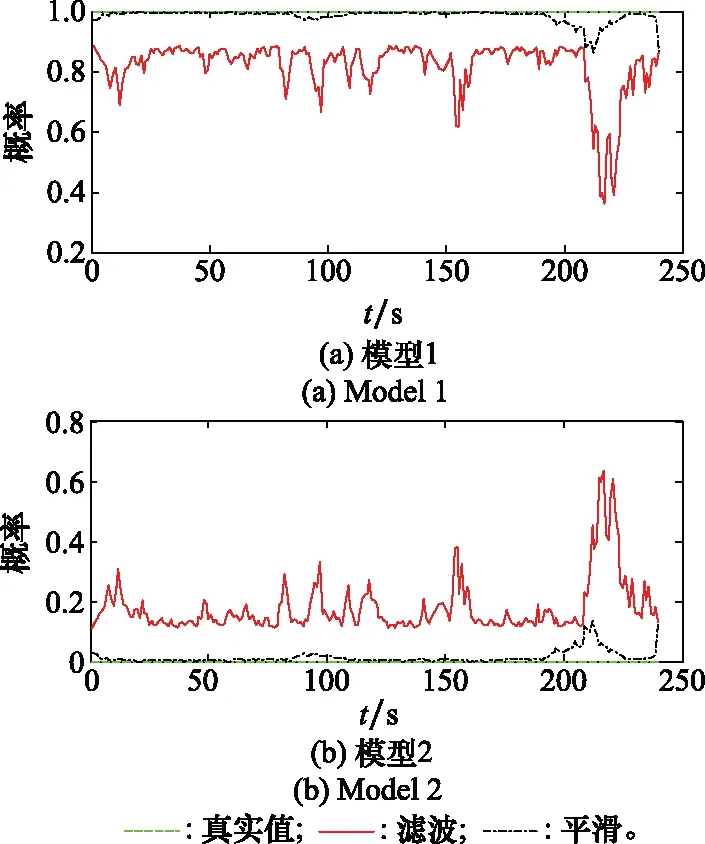
图4 无人机模型概率估计

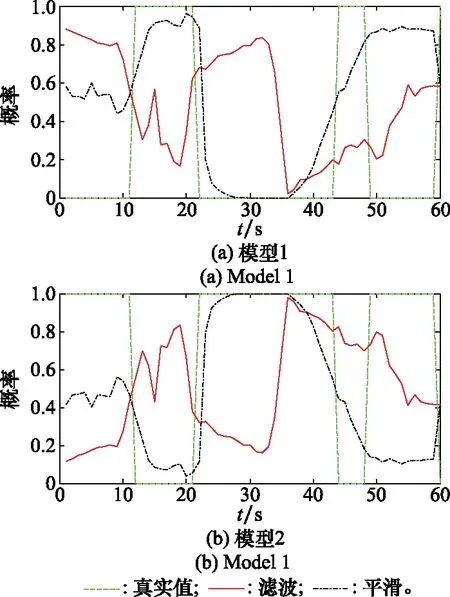
图5 飞鸟模型概率估计

图6所示为通过不同数目的跟踪步数,滤波算法生成的基于1 000次蒙特卡罗仿真的接收者操作特征(receiver operating characteristic, ROC)曲线。可以看出,步数越多,分类效果越好。原因显而易见,跟踪步数越多,无人机飞行轨迹的稳定性和飞鸟目标的机动性就表现的越明显,因此更容易准确分类。图7和图8显示了在不同模型变化概率下采用滤波和平滑算法的ROC曲线,跟踪步数设置为NT=50。P值越大,目标运动模型的变换频率越高,越容易分类。从图7和图8中可以看出,无论是滤波还是平滑算法,当无人机目标检测率接近100%时,飞鸟目标的虚警率都小于15%。总体上,经过平滑处理的目标分类结果优于基于跟踪滤波的目标分类结果。

图6 不同跟踪步数下的滤波算法ROC曲线

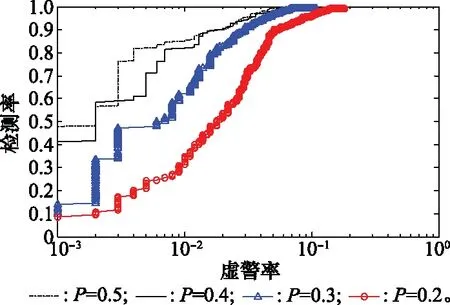
图7 不同模型转换概率下的滤波结果ROC曲线

图8 不同模型转换概率下的平滑结果ROC曲线

图9给出了参数设置为P=0.2时,滤波和平滑算法获取的目标分类ROC曲线的对比结果。与单独采用滤波处理相比,平滑处理进一步提高了两类目标估计结果的区分度,提高了目标分类的准确率，图4和图5的模型概率估计结果示例同样验证了该结论。

图9 滤波与平滑算法的ROC曲线比对

2.3 算法复杂度分析

目标轨迹平滑算法明显提高了目标分类的准确度,但同时也增加了算法的复杂度。本节在Inter(R)/Core(TM)/i5-4690/CPU@3.50GHz台式机处理器、4.0 GHz内存、Matlab R2014a的运行环境下,通过100次蒙特卡罗仿真实验,对每条轨迹进行滤波和平滑处理的平均耗时进行统计,结果如表2所示。在目标轨迹跟踪步数不同取值(NT分别取30, 40, 50)的情况下,滤波和平滑处理的总耗时约为滤波处理的3倍多。当目标跟踪步数NT=50时,目标的分类效果最优,此时每条目标轨迹的平均滤波处理时间为0.014 4 s,而每条目标轨迹的平均滤波和平滑处理时间为0.054 1 s,但仍可满足实时处理的要求。

表2 目标轨迹跟踪平均耗时

3 实测数据分析

利用自行搭建的低空预警雷达系统[29],积累了大量低空目标的原始雷达数据。本节将处理和分析两组外场收集的雷达数据,实验中提高了无人机目标飞行轨迹的机动性,充分验证了算法的可行性。

3.1 实例1

本节给出了一个岸基低空预警雷达应用的实例。图10所示为安装在海岸附近高层建筑上的雷达系统。测试的无人机目标进行了一次往返飞行,探测半径达3 km。除了无人机,雷达数据中的目标大多是沿海水鸟。表3和图11给出了本例中无人机和飞鸟目标的分类结果。本例中,无人机沿直线进行往返飞行,本身识别难度不大,但是水鸟在海上的飞行方式同样以滑翔为主,机动性略低,更接近无人机。因此,当阈值设置为S=0.000 1时,雷达数据中的鸟类和无人机能够被完全正确区分,如图11(c)所示。阈值S反映了目标运动模型的变化情况,当S取值增大时,飞鸟目标被误识别为无人机的数量也相应增多。总体上,轨迹平滑后的分类准确率高于跟踪滤波的分类结果。

图10 某岸基低空预警雷达

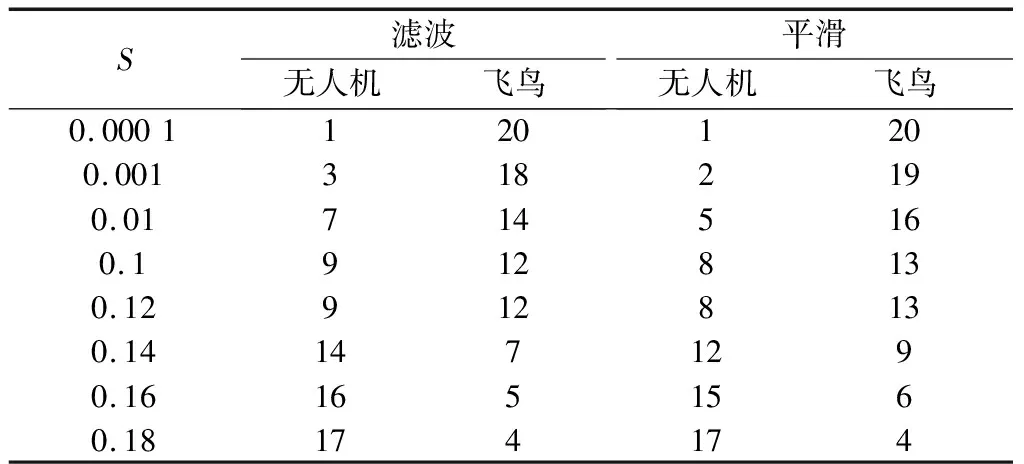
表3 实例1中飞鸟与无人机目标的识别结果

3.2 实例2

本节给出了一个机场应用的实例。图12所示为安装在某通用机场灯光站屋顶上的低空雷达预警系统,采用水平机械扫描方式。图13所示为特定时间段内采集的雷达数据,探测半径为5 km,量测数据“°”叠加在卫星地图上,无人机和飞鸟的跟踪轨迹分别由实线和“□”表示。测试无人机为大疆精灵4,实验中模拟了无人机沿曲折路线逼近机场的情况,目标4次变更其飞行方向,部分时段沿切向飞行,极大增加了雷达跟踪的难度,但雷达系统足够的数据更新率仍然保证了跟踪的稳定性。雷达数据中的飞鸟多为觅食中的小型鸟,飞行距离短,机动性强。

图12 某通用机场低空预警雷达

无人机和飞鸟目标在不同阈值下的跟踪识别结果如图13所示。该算法跟踪步骤的数目设置为NT=50。当阈值很高时,一些机动性不高的飞鸟被错误分类为无人机。图13(a)中,阈值设置为S=0.04,实现了全部目标的正确分类。参照图13,表4给出了不同阈值下的分类结果。在本例中,轨迹平滑后的分类准确率总体上仍然优于跟踪滤波的分类结果。

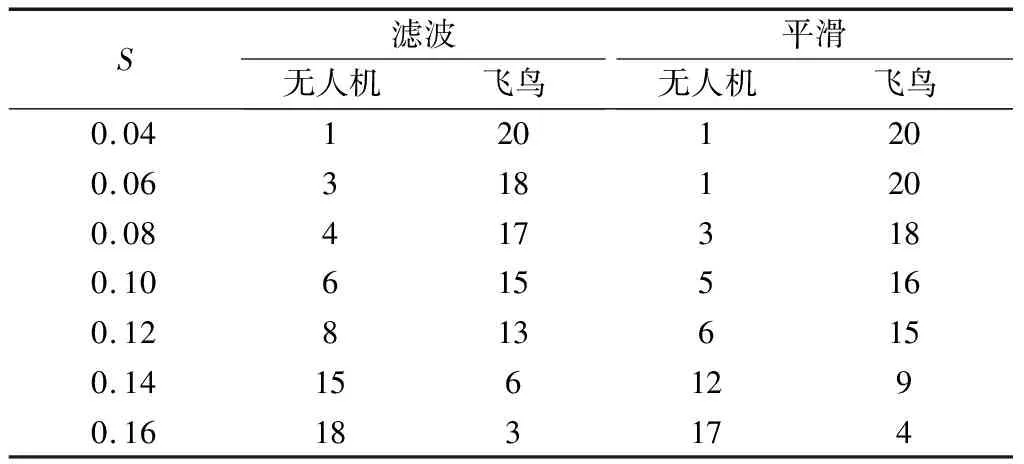
表4 实例2中飞鸟与无人机目标的识别结果

在实际应用中,首先需要对部分无人机和飞鸟目标轨迹进行人工分类标定,通过积累实验数据估算模型转换概率,进而确定合理的阈值。实际上,在各类应用场景中,系统阈值可能发生变化,目前可行的办法是通过实验统计结果进行调整,以保证分类效果。

4 结 论

本文提出一种基于雷达目标轨迹跟踪滤波与平滑的低空目标分类方法,在前期研究的基础上,进一步改善了分类效果,得出以下结论。

(1)该算法利用有限的目标回波信息,初步实现了无人机和飞鸟目标的分类,适用于常规的非相参机械扫描预警雷达,为实现低成本雷达的目标分类技术进行了有益探索。

(2)仿真实验结果表明,平滑算法能够扩大飞鸟和无人机目标模型转换频率联合估计值之间的区别,在目标分类准确率上明显优于单纯的跟踪滤波算法;平滑算法虽然在算法的复杂度方面有所增加,但仍在可接受范围内,一般的硬件运行条件即可满足实时处理要求。

(3)实验中多次改变无人机飞行方向,增加了雷达跟踪难度,但只要保证一定的目标跟踪步数,就基本不会对目标的分类结果产生影响;但是,对于一些机动性较低的飞鸟,其轨迹特征与无人机相似,可能导致分类错误。

(4)除目标轨迹特征之外,利用RCS、目标速度、极化特征等多维度目标信息,结合深度学习方法的传统机械扫描雷达目标分类技术,将成为此领域未来的研究方向。