轻量化的增量式集成学习算法设计

丁嘉辉, 汤建龙, 于正洋

(西安电子科技大学电子工程学院, 陕西 西安 710071)

0 引 言

常规的分类与回归树算法(classification and regression tree, CART)作为一种典型的决策树算法,其结构简单、判决速度快、可解释性较好[1],发展到现在已有多种变体与改进形式[2-3],广泛应用于各种分类问题[4-8],在集成学习算法中也被认为是一种非常有效的基分类器。例如经典的随机森林算法[9-13]就是以CART作为基分类器,通过投票的方式综合所有基分类器的判决结果。但是常规的CART与集成学习算法也存在一个缺点,一旦有新类别进入分类范畴,算法模型通常需要重新训练来实现对新类别样本的认知,在分类类别数量较多时这将导致训练时间的大幅度增加[14]。这一问题限制了CART算法在更复杂情景中的应用。例如在电子侦察领域,已经广泛采用极限学习机[15-16]、集成学习等算法来解决辐射源分类问题[17-20],我们经常需要扩充分类器能够识别的样本类别库,来适应复杂多变的战场环境,如果每次都重新训练分类器模型必然会大幅度增加计算量。

针对上述问题,本文提出了一种轻量化的增量式集成学习算法。首先,让原有CART的叶节点再生长,在不破坏现有结构的基础上使之具备开集识别的能力,从而能够辨别训练集类别之外的异常样本。然后采用增量式的集成策略[21-23],以若干个具有开集识别能力的CART作为基分类器构成增量式集成学习算法,每个基分类器只负责其中一部分类别的分类。开集识别能力确保了每个基分类器只会对自己“认识”的样本做出判决,否则投出“弃权票”。因此,当需要扩充新的分类类别时,只需添加对应的基分类器,所需的训练时间将远远低于重新训练整个模型所花费的时间,从而简化学习过程,降低计算复杂度。

1 CART的开集识别改进算法

1.1 CART基本原理

CART算法采用基尼(GINI)系数的增益来筛选每个节点的分裂特征与分裂值。假设样本共分为K类,令|D|表示进入当前节点样本集D的样本数量,|Dk|则表示其中第k类样本Dk的数量,GINI系数定义如下:

(1)

式中,pk表示样本属于第k类的概率,采用|Dk|/|D|作为概率估计。GINI系数与信息熵有着类似的数学特性,GINI系数越小,则说明样本的纯净度越高。

以连续型特征为例,CART节点的每次分裂都将当前样本一分为二。定义条件基尼系数

Gini(y|A)=p(A≤α)Gini(y|A≤α)+

p(A>α)Gini(y|A>α)

(2)

来表示样本集在选取特征A和对应的分裂值α作为分裂标准后的GINI系数,其中

(3)

可得经验条件GINI系数为

Gini(y|A)=

(4)

式中,|D1|和|D2|表示分裂后的两个数据集大小;|D1k|和|D2k|为分裂后的分别属于第k类的样本个数。从而可以定义GINI增益为

GGini(y,A)=Gini(y)-Gini(y|A)

(5)

用来表示当前分裂方式对样本集纯净度的提高程度,从而筛选出最优的分裂标准。

下面给出了CART生成的基本算法步骤如下:

步骤1获取进入当前节点的样本集D。

步骤2如果样本集D中所有样本属于同一类别(或者该类别占比超过某一比重),则停止生长形成叶节点,并将该类别作为当前节点的类别。否则,继续生长。

步骤3获取样本集D中所有潜在的分裂特征与对应的分裂值取值集合,并分别计算每一种分裂方式的GINI增益,保留其中使GINI增益取得最大值的分裂特征与分裂值。

步骤4按照步骤3获取的分裂方式生成两个子节点,并将样本集D分裂成D1和D2分别进入这两个节点,重复步骤1。

1.2 开集识别改进

常规CART叶节点的最终形成,是以单个特征为依据,将一类样本从样本集中分离。例如图1所示的某次节点分裂中,特征A以α为分裂值,将类别k的样本从样本集中剥离出,形成一个叶节点;剩余样本则进入另一个子节点中,继续分裂或者同样生成叶节点。

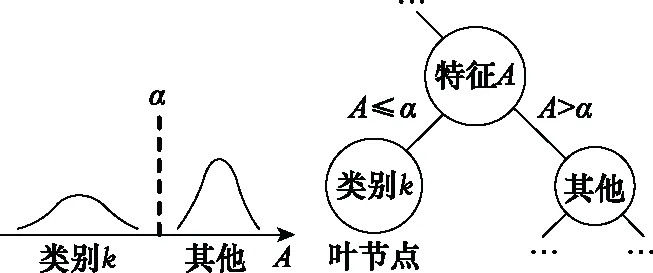
图1 叶节点生成示意图

这种叶节点的生成方式可以区分训练集中包含的类别,但无法识别训练样本类别之外的异常样本。为了使CART具备开集识别的能力,考虑对进入叶节点的待测样本进行二次确认,当且仅当待测样本的各维度特征值符合训练集在叶节点的分布范围时,才给出分类判决,否则认为待测样本异常。图2给出了对一个叶节点做开集识别改进的示意图。

图2 叶节点的开集改进示意图

假定进入原CART叶节点中的所有样本属于同一类别,统计特征向量中每一维度特征值Ai的分布,估算该特征值的取值下限Aimin与取值上限Ai max,并以此作为分裂值完成两次节点分裂,从而把不在该特征值取值范围内的待测样本划分为异常类(None)。对每个维度特征值做与上述相同的两次节点分裂操作,将最后的叶节点标记为原叶节点所属类别,作为最终输出的有效分类判决。

根据上述思路,不改变原有CART生成算法,仅在生成叶节点时执行以下步骤:

步骤1获取进入当前叶节点的训练样本集D,并剔除其中所有不属于叶节点类别的样本。对特征向量中的每一维度特征Ai(i=1, 2, …),循环执行步骤2～步骤4。循环结束后执行步骤5。

步骤2利用样本集D估算特征Ai的取值下限Aimin与取值上限Aimax。

步骤3以特征Ai和分裂值Aimin对当前节点做分裂,将左子节点标记为异常类(None),并进入右子节点。

步骤4以特征Ai和分裂值Aimin对当前节点做分裂,将右子节点标记为异常类(None),并进入左子节点。

步骤5循环结束后,将当前节点标记为原叶节点所属类别,结束分裂。

上述改进算法并没有破坏CART原有的结构与生长方式,数据样本在节点分裂中的分布情况也保持不变。由于只对叶节点做了改动,甚至可以直接在已有CART模型的基础上修改而不影响原有的判决逻辑。

2 基于改进CART的增量式集成学习算法

2.1 算法原理

集成学习算法对样本的认知是由它所有基分类器综合体现的,因此通过修改其中基分类器的组成成分,就可以实现对集成学习算法分类器整体功能的调整。本文认为,如果基分类器具备开集识别的能力,将使这一过程变得非常简单。以常规CART作为基分类器的集成学习算法只能区分训练样本中包含的类别,如果要增加新的分类类别,必须将新老样本混合作为训练集重新构建所有的基分类器,否则原有基分类器对新类别样本必定会做出错误的判决[24-25]。而开集识别可以使分类器屏蔽那些不属于训练集类别的外来样本,从而只对已知类别范畴内的样本做出分类判决。

图3给出了具备开集识别能力的增量式集成学习算法做出分类判决的示意图。待测样本以特征向量的形式进入集成学习算法,由每个基分类器独立做出分类判决,只有那些具备该类样本训练知识的基分类器才会做出有效的判决,其余的基分类器均给出“弃权票”,最终的输出结果将只取决于所有的有效判决。因此,只需在原有集成学习算法中添加同样具有开集识别能力的基分类器,就可以使算法在识别新类别样本的同时,不影响原有类别的分类效果。

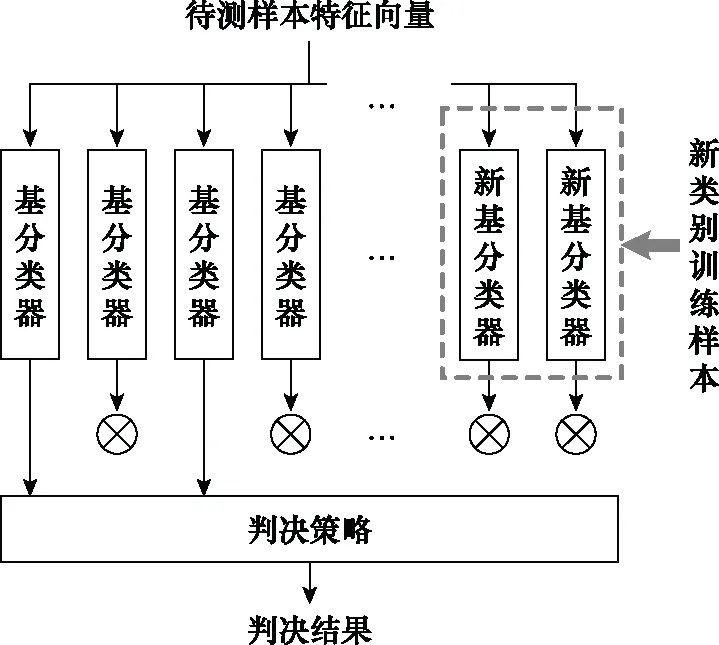
图3 增量式集成学习算法判决示意图

在上述集成学习算法中,判决策略做出最终判决的一个充分条件是:在所有基分类器的有效判决中,某一类别占据多数。若待测样本的类别标号为k,包含类别k的基分类器数量为N,其中做出正确且有效判决的数量为n,做出无效判决的数量为n0,其余的则是错误但有效的判决;而不包含类别k的基分类器数量为M,其中做出无效判决的数量为m,其余的也必然是错误但有效的判决。上述充分条件可以表示为

n>N-n-n0+M-m

(6)

即

2n+n0+m>N+M

(7)

假设所有基分类器相互独立,且具有相同的集合内分类准确率ptest和开集识别准确率popen,那么满足该充分条件的概率为

(8)

特别地,如果所有基分类器包含的类别互不重叠(即N=1),那么有

(9)

可以看出,集成学习算法的分类准确率会随着基分类器的数量呈现出指数下降的形式。因此,让基分类器维持较高的开集识别准确率是这一增量式算法的重要保证。从“稳定-可塑性”[26]的角度看,当集成学习算法中增加基分类器时,新基分类器的开集识别能力保障了原有分类器的分类效果,即“稳定性”;而原有基分类器的开集识别能力则给新基分类器的加入提供了足够的空间,即“可塑性”。因此,让基分类器维持较高的开集识别准确率也有助于解决增量式算法的“稳定-可塑性”问题。

2.2 计算复杂度分析

增量式算法最主要的一个优势体现在:对一个已有模型进行修改的计算代价远低于重新训练一个模型所需的代价。下面将对CART算法与增量式集成学习算法的建模过程进行计算复杂度分析。

根据CART决策树生成的算法流程分析可知, GINI增益的多次计算占据了绝大多数运算资源。令ND为特征向量维度,K为样本的类别数量,NK为每个类别包含的训练样本数量,Ndiv为CART节点的分裂次数(即非叶节点的个数)。考虑到每一次节点分裂时,都要在每个特征维度遍历当前节点中的所有训练样本,并计算每一种潜在分裂方式的GINI增益,所以CART的计算复杂度可以表示为

TCART(K)=O(NdivNDNKK)

(10)

而通常情况下,分裂次数Ndiv是关于类别数K的线性复杂度,因此

TCART(K)=O(NDNKK2)

(11)

再分析对CART做开集识别改进的计算复杂度。基于原有CART模型,改进算法在每个原有的叶节点上做了2ND次额外的节点分裂,令Nleaf为原CART中叶节点的数量,由于进入叶节点的样本数已经下降至NK,所以计算复杂度可以表示为

Topen(K)=O(NleafNDNK)

(12)

又因为叶节点数量始终满足Nleaf=Ndiv+1,也是关于类别数K的线性复杂度,因此

Topen(K)=O(NDNKK)

(13)

集成学习算法的计算复杂度是其所有基分类器的计算复杂度之和。假设将所有类别划分成Ng组,每一组包含的类别数为Kg,而且每一组都利用对应训练样本构建Nt个具有开集识别能力的CART作为基分类器,并最终组合成集成学习分类器。所需的计算复杂度为

Tensemble(K)=O(NgNt(TCART(Kg)+Topen(Kg)))=

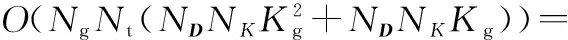
(14)

又因为类别数K=NgKg,所以

Tensemble(K)=O(NtNDNKKgK)

(15)

根据上述分析,假设每个类别包含的训练样本数量NK不变,CART生长过程的计算量是关于类别数K的平方复杂度,而对CART做开集识别改进的计算量是关于类别数K的线性复杂度。集成学习算法的计算量受到基分类器个数与单个基分类器计算量的影响,通过分组减少每个基分类器的训练样本类别数可以降低算法整体的计算量。当每组类别数Kg不变时,集成学习算法的计算量是关于总类别数K的线性复杂度;而总类别数K不变时,降低每组类别数Kg可以线性地降低计算量。

3 仿真与分析

仿真实验以辐射源分类问题为背景,通过对比常规CART算法,研究本文所述增量式集成学习算法在计算复杂度与分类效果上的表现。仿真数据中包含了不同信噪比(信号与噪声的功率之比)下132个类别(随机标号为1～132)的辐射源脉冲信号样本,数据处理流程如图4所示。从包含不同辐射源参数的数据库中随机抽取132类,产生信号层数据流,叠加不同功率的噪声来模拟不同的信噪比环境,经过包络检波与快速傅里叶变换(fast Fourier transform, FFT)频谱分析,提取6个维度的特征——脉宽、中心频率、脉首频率、脉尾频率、带宽、调频斜率,作为每个样本的特征向量,计算它们在不同信噪比下的标准差如表1所示,信噪比降低(当信号功率不变时噪声功率增大),会导致各特征值的测算误差变大。

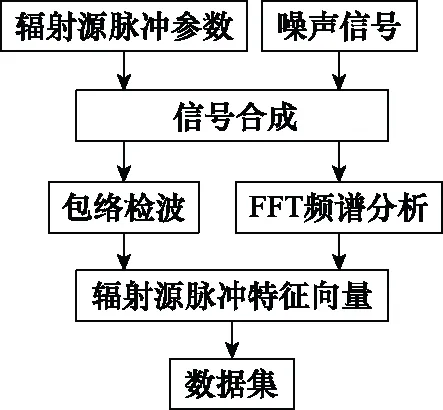
图4 辐射源数据处理流程

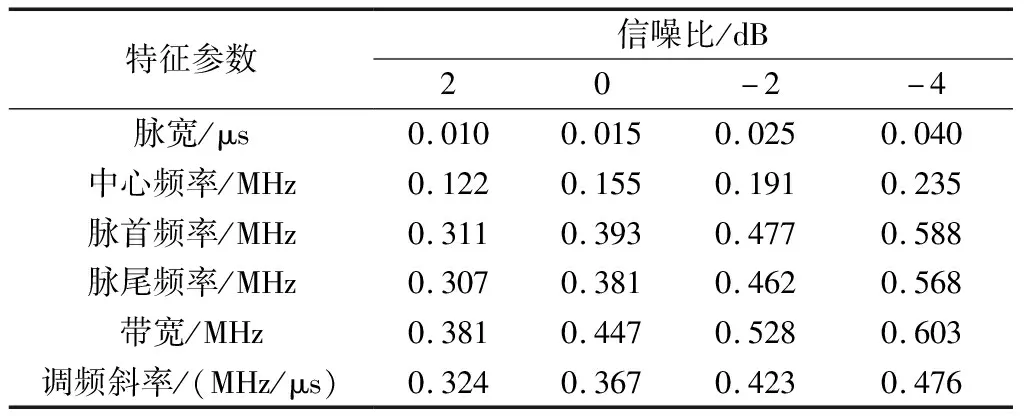
表1 不同信噪比下各特征参数的测算标准差

在-4～2 dB的信噪比范围内,随机从每一类辐射源脉冲样本选取60个,产生共计7 920个特征向量作为训练集,分别根据常规CART算法与增量式集成学习算法进行如下实验,实验流程如图5所示。

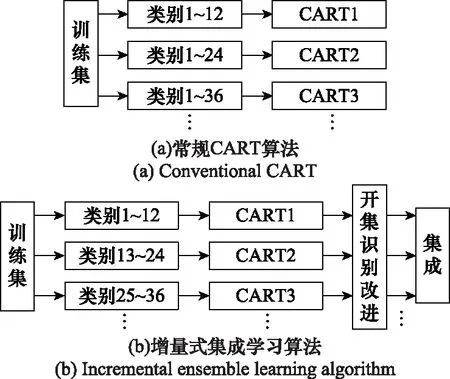
图5 仿真实验流程

(1)常规CART算法:从包含12个类别的训练集(720个样本)开始,每次增加12个类别的(720个)样本扩充原有的训练集,训练集1包含类别1～12,训练集2包含类别1～24,训练集3包含类别1～36,以此类推到训练集11,并在每个训练集的基础上构建常规CART分类器,以此模拟分类类别的扩充。如图5(a)所示。

(2)增量式集成学习算法:将样本类别1～132依次分成11组,每组12类,以每个组的720个样本作为一个训练集,训练集1包含类别1～12,训练集2包含类别13～24,训练集3包含类别25～36,以此类推到训练集11,在每个训练集的基础上分别构建一个CART分类器并做开集识别改进。将这11个CART作为基分类器,逐个添加到增量式集成学习算法中,以此模拟分类类别的扩充。如图5(b)所示。

本文所有结果是在Ryzen 2700X、16G内存、64位操作系统环境下,以单核单线程运行所得。本实验随机从辐射源数据库中抽取特征参数生成数据集,进行有关计算复杂度和分类效果的仿真,重复8次,最终结果取平均值。

3.1 计算复杂度仿真

本文采用浮点数运算次数(floating-point operations per second, FLOPs)来衡量训练过程的计算复杂度。随着分类类别的扩充,分别计算常规CART算法和增量式集成学习算法的FLOPs数值变化,得到关于类别数量的变化曲线如图6所示。图7则给出了这两种算法在训练过程中的实际耗时曲线。

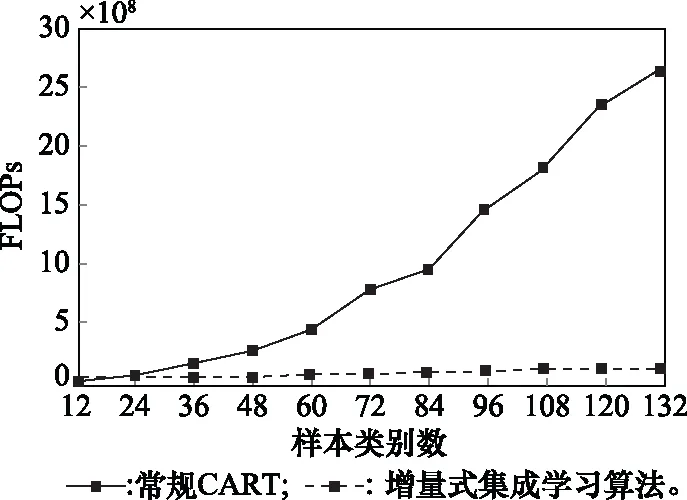
图6 FLOPs曲线

图7 实际耗时曲线

实验结果基本符合本文第2.2节对计算复杂度的分析,其中常规CART算法是关于样本类别数的平方复杂度,而本文所述的增量式集成学习算法是关于样本类别数的线性复杂度。根据FLOPs曲线,为了最终实现132类样本的分类,后者所需的计算量仅是前者的1/22。从增量的角度看,常规CART算法扩充分类类别时必须重新训练整个模型,而增量式集成学习算法只需增加对应的基分类器。当分类类别数量从120类扩充到132类时,增量式集成学习算法所需的计算量仅仅是常规CART的1/213。可以看出,在分类类别数量较多时,本文所述增量式集成学习算法在降低计算复杂度上具有明显的优势。

需要说明的是,FLOPs曲线没有考虑CART在节点分裂、后剪枝过程中的额外计算开支与内存分配,而增量式集成学习算法在新建基分类器时重复了这些步骤,所以它的实际耗时曲线比FLOPs曲线具有更大的上升斜率,但这并不影响上述结论。

3.2 分类测试

以不同信噪比环境下的132类信号脉冲样本作为测试集,其中每个类别包含40个样本。对增量式集成学习算法中的11个基分类器依次进行以下3组测试:① 使用与训练集相同类别的测试集(12类共480个样本)评估CART在开集识别改进之前的集合内分类准确率;② 采用相同的方法评估CART在开集识别改进之后的集合内分类准确率;③ 使用训练集类别范围外的测试集(120类共4 800个样本)评估每个CART在开集识别改进之后的集合外异常检测率(开集识别准确率)。本文将集合内分类准确率定义为

(16)

式中,Ncorrect表示正确分类的样本数;Nin表示训练类别范围之内的测试样本数。集合外异常检测率定义为

(17)

式中,Nopen表示正确识别为异常样本的数量;Nout表示训练类别范围之外的测试样本数。依次在-4 dB、-2 dB、0 dB、2 dB信噪比环境下,统计各基分类器的识别率均值,得到表2所示结果。

表2 CART开集识别改进前后的分类准确率

结果表明,对CART做开集识别改进会在一定程度上影响集合内的分类准确率,但是这一改进的好处是可以使基分类器具备集合外异常样本的检测能力,而且始终保持了很高的准确率,从而让具有不同分类类别的基分类器可以同时存在于一个集成学习算法中。如果某一特征向量被所有基分类器都识别为异常样本,就有理由认为该特征向量不属于整个训练集的类别范围,从而实现集成学习算法整体的开集识别。

进一步地,为了观察不同信噪比环境下,常规CART算法和增量式集成学习算法在扩充类别数量时分类准确率的变化,进行以下测试。分别在-4 dB、-2 dB、0 dB、2 dB信噪比环境下各取一组数据作为4个测试集,其中每个测试集都从各辐射源类别中随机选取40个脉冲样本(即每个测试集包含132类共5 280个特征向量)。得到常规CART算法和增量式集成学习算法的集合内分类准确率随着类别数量增加而变化的曲线如图8和图9所示。

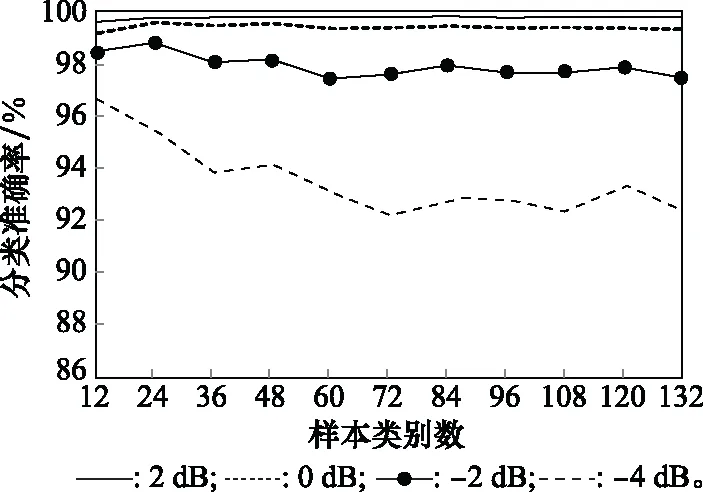
图8 常规CART分类准确率变化曲线

图9 增量式集成学习算法分类准确率变化曲线

实验结果表明,两种算法在信噪比较高的环境下都能维持很高的分类准确率,而随着信噪比的下降,它们的分类准确率也都产生了不同程度的下滑。其中增量式集成学习算法的分类效果稍逊于常规CART算法,但在信噪比大于等于-4 dB的环境中依然能保持90%以上的分类准确率。另外,随着类别数量的增加,两种算法的分类准确率也表现出了不同程度的下降趋势,不过由于增量式集成学习算法的基分类器始终具有很高的集合外异常检测率(见表2),增加新的基分类器对原有集成学习算法分类效果的影响十分微小,使之在类别数量较多时依然能维持较高的分类准确率。

4 结束语

本文提出了一种轻量化的增量式集成学习算法,通过开集识别改进保证CART基分类器只会对已知的样本做出有效判决,从而可以通过添加基分类器的方式来扩充集成学习算法能够识别的类别范畴。以辐射源分类为背景的仿真实验表明,该算法可以实现关于类别数量的线性计算复杂度,大幅度降低新增分类类别所需训练成本;该算法的缺点是牺牲了少量的分类效果,但在一定信噪比范围内依然能保持相对较高的分类准确率。

本文的仿真实验只讨论了一种最简单的集成方式,即每个CART基分类器所能识别的样本类别互不重叠,每次分类最多只有一个基分类器能做出正确的判决。如果不同基分类器的可识别类别互有交集,理论上会增加正确判决出现的概率,从而提高增量式集成学习算法整体的分类效果。这将是下一步的研究工作。