用问题助推学生思维能力的发展

【摘要】本文以“围棋中的数学问题”的教学为例，论述促进学生思维能力发展的方法，提出在讨论中发现并提出问题、在动手探究中辨析问题、在动笔勾画推演中解决问题、在学情评析中增强问题意识等教学建议，发展学生的思维能力。

【关键词】小学数学 思维能力 培养策略

由于小学生的认知水平有限，再加上不成熟的心理特征以及尚未健全的思维能力，导致他们在认识新事物的初期受情绪和直觉的影响较大，而自动联系书本知识形成理论的科学认知的能力较为薄弱，他们往往只关注外表，注意表面现象，不能透过现象看本质，不能按照一定的顺序来观察。所以，笔者充分调动学生的积极性，引导他们在激烈的争辩中启迪智慧，碰撞出思维的火花，激发他们发现和提出问题的灵感。下面，笔者以“围棋中的数学问题”为例，谈谈如何促进学生思维能力的发展。

一、在讨论中发现并提出问题

在教学“围棋中的数学问题”时，笔者先对围棋做了较为专业的介绍，然后创设一个具体的教学情境：围棋棋盘的外层每条边有19格，每边可以落子19枚，那么最外围一共可以落子多少枚？学生试图口算，但由于这个问题具有一定的难度，学生得出的答案五花八门。笔者暂时不给予纠正，而是让学生自己交流，进而在沟通中发现不对劲的地方：这到底是怎么回事？哪里出纰漏了？有学生在研究围棋棋盘后发现其中的奥妙：有的学生将四个边角上的四个格点重复计算，每个格点算了两次。学生猛然醒悟，发现了一个有意思的问题：怎样计算才能做到每个格点只算一次？最外围每边的格点数与格点总数之间存在什么样的数量关系？这正是本节课研究的重点。问题的提出是在深度思考的前提下进行的，并且是由学生自发组织的，是受学生的内驱力驱动的，这种发现问题的过程是一种自我提升的过程，不仅可以体验到成功的喜悦，更是大大提升了学生的学习兴趣。在引导学生探究时，教师应尽可能地激发学生的好奇心和探究欲，引导学生主动质疑和提问。

二、在动手探究中辨析问题

新课标将义务教育阶段数学学科的总目标由“双基”调整到“四基”，明文规定学生应“获得适应社会生活生产的基础知识、基本技能、基本思想、基本活动经验”。其中“基本活动经验”是培养学生数学素养的重要标志和衡量指标。不管什么样的活动经验，不外乎都是在“做”和“思”的双重作用下沉淀的，在学习数学知识和技能的漫长进程中渐渐积累的。因此，在教学“围棋中的数学问题”一课时，笔者创设了两个研究型活动以突破本课的重难点。第一个研究型活动：通过在网格中摆放棋子，探究围棋盘最外围每边的格点数和外围格点总数之间的数量关系。呈现2×2、3×3、4×4网格图，即最外围每边分别尝试摆放3枚棋子、4枚棋子、5枚棋子，计算外围摆放的总棋子数。学生在网格图中摆弄、点算，并填写棋子的总数，再观察数据之间的变化关系，四人小组开展组内交流：发现了棋子数量的变化规律没有？通过亲自动手实践及观察商量后，学生归纳出不同的解题方法：

①最外围放置的棋子总数=（外围每边放置的棋子数目-1）×边数;②最外围放置的棋子总数=外围每边放置的棋子数目×边数-4;③最外围放置的棋子总数=外围每边放置的棋子数目×2+（外围每边放置的棋子数-2）×2。

然后再采用不同的方法解决例题便显得顺理成章。

第二个探究活动：通过动手摆棋子或打点，研究封闭路线上植树问题的间隔数和总棵数之间的对应关系。这节课其实是植树问题的变式，围棋落子数是表面，而植树问题才是其本质，研究的中心问题是间隔数和植树棵数之间的对应数量关系。为了便于观察和抽象，笔者借助动画课件辅助教学：将棋盘内的网格线淡出，围棋棋子逐渐“变成”一棵棵小树，将围棋问题彻底还原为封闭路线上的植树问题。借机指引学生思考并提问：在封闭路线上植树时，间隔数和树木的棵数之间存在什么对应关系？呈现常见的封闭图形：

引导学生通过打点、画圈或者摆棋子代替种树，清数每条封闭路线上植树的棵数与间隔数各是多少。在集体商议中学生概括出：间隔数=总棵数。从学生反馈的情况看，这一系列基本活动经验的积累大大提高了数学学习的效率。由此可见，在小学数学课堂教学中，教师要强化学生的动手操作活动，保证学生有足够的时间和空间观察、猜测、推导、商讨等。

三、在动笔勾画推演中解决问题

新课程改革施行以来，教师越来越重视学生的动手能力与合作探究及溝通协商能力的培养。事实上，学生需要的不仅是观察与思考、操作与交流，更为迫切的是对知识和思路的梳理、概括与升华。学生能否将在操作中感悟到的知识学以致用，解决具体问题，需要教师布置适量的书面作业来检验。现实生活中与“植树问题”类似的问题数不胜数，如公路旁安装太阳能路灯、花坛边花盆的摆花、方阵队列的排列、打绳结、上楼梯等。由于这些问题的本质都是对间隔数与棵数之间数量关系的转换，因此，教师要甄选典型的“植树问题”作为此类问题的通用模型，探索出解决这一类问题的基本模式。在应用规律解题时，笔者精挑细选了三个呈现梯度的问题让学生课余时间笔答。

应用练习：假设四边形每条边上都放置7枚棋子（边角上也要摆放），一共可以落子多少枚？假设是六边形，每条边上都摆放9枚棋子（边角上也摆放），一共可以落定多少枚棋子？假如在圆周上摆放5枚棋子，圆周上一共有几段间距？

基础性问题：假设要在五边形的草地上栽种向日葵，使每一边都种上4棵向日葵，可以怎样设计？最少需要预备几株向日葵？圆形露天广场的周长是150米。假设沿着边缘每隔15米插上一面红旗，一共需要多少面旗帜装点？

延伸性问题：迎接国庆节，学校举办团体操演出。六一班学生排成方阵，最外圈每边站立15人，最外圈共排列了多少名学生？整个方阵一共容纳多少人？

除此之外，教师还要教给学生书面表达的一般方法和策略，让学生清楚地知道如何准确完整地回答问题，如何科学规范地记录实验过程和数据。

四、在学情评析中增强问题意识

所谓的问题意识，是指学生在接触和了解事物的过程中，面对超出现有知识和能力范围的疑虑和困惑，提出自己的想法，并产生期待解释疑惑的欲望。学生有了问题，才会产生思考的动机;只有不断地探索才有机会去创新，才有机会获得长足的发展和进步。问题意识的培养已成为数学教育目标中的重要部分。事实证明，问题意识浓厚的学生、善于提出疑问的学生，他们都能深刻地认识和理解知识，遇到棘手复杂的问题也能冷静而理智地分析，积极寻找解决办法。然而现实情况却令人堪忧，学生的问题意识淡薄，不敢问、不愿问、不想问、不会问，这就需要教师营建“大胆提问”的民主氛围，保护学生“提问”的积极性，对学生提出的问题及时给出客观公正又专业的评析。

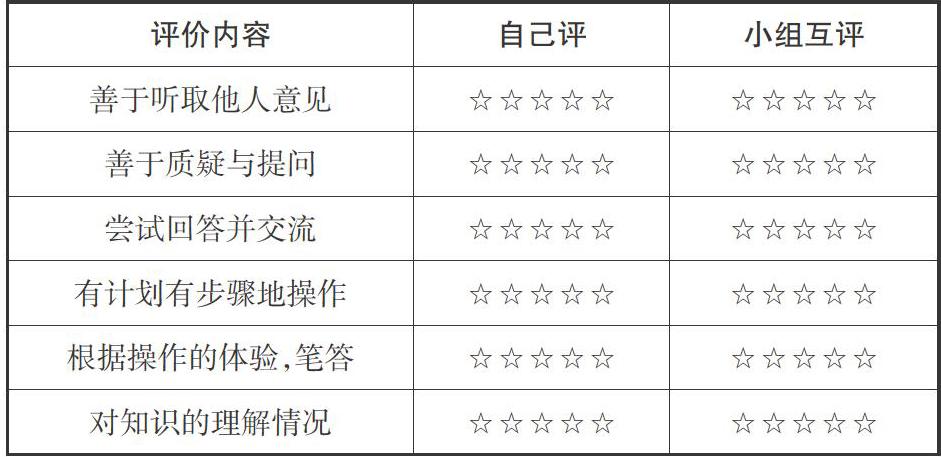
因此，根据这节课的内容，笔者量身打造了如下的评价表格，让学生自评后在小组里互评。“同学们，学完这节课，你有哪些收获？你的表现到底如何？快来涂画小星星吧！涂得越多，表现越好哦。”

总之，在数学教学实践中，只有全力培养学生的问题意识，优化教案，真正使学生在活动中产生内心的渴求，才能达到悟透数学本质的境界。

作者简介：覃金玲（1975— ），女，广西北流人，大学本科学历，一级教师，主要从事小学数学教学研究。

（责编 林 剑）