千里莺啼绿映红 杏坛思索处处春
——浅谈数学问题的有效设计
毛葆媛
(江山市石门初级中学 浙江衢州 324100)
有效数学问题是指能有效促进学生发展,有效实现预期教学结果的数学问题。有效数学问题的设计包含数学教师对题目的有效设计和对提问的有效设计。在课堂教学中教师设计的数学问题要尽可能多地为学生提供观察、操作、交流的机会,引导学生进行积极的思考,提高学生的数学思维能力和数学学习能力,有效课堂教学依赖于教师对问题的有效设计[1]。让我们先看下面的案例:
案例:某九年级“相似三角形”的复习课上,A教师在简单复习了相似三角形边与角的关系后,直接给出例题:
在矩形ABCD中,AB=5,AD=2,E是DC上的一点且DE=4,连接AE并延长,交BC的延长线于点F。

(1)求线段FC的长。
(2)连结BE,求证:△ADE∽△ECB。
(3)判断△ABE的形状,并说明理由。
分析:从A教师设计的题目来看,教师机械地让学生复习了三角形全等判定的条件后马上出示例题,整个题目通过媒体直接投影呈现,模式单一,很难引起学生的共鸣和兴趣。教师就题论题,学生难以理解教师设计此题的目的,学生也纯粹为了解题而解题。对于第(2)小题相似的证明,教师并未考虑到学生的原有水平,由于学生习惯用“角等”来判定相似,没有前序的准备,很多学生都没有想到用边的关系来证明,因此在解题时存在障碍。
从A教师的课堂提问来看,提问方式比较陈旧,在第(2)小题,教师为了说明证明相似除了找角等的方法外还有找对应边成比例的方法,于是向学生提问:“找角好找吗?不好找我们试试边,可以吗?”我想,对于这个问题,教师可以这样处理:先请学生来找相似的条件,若学生找不到,再提问:“你为什么找不到呢?”“判定三角形相似的条件有哪些?”“你是从哪个角度出发思考问题的?”“我们可以试试其他方法吗?”学生通过这些问题的解决可以自己发现解题方法,能够提高学生的学习主动性。
可见,有效的问题设计应该以学生为本,教师要善于根据教学内容和学生实际,设计有价值、有效果的数学问题。教学中设计有效的问题是实现有效教学目的的重要方法,是成就精彩课堂的必要因素。因此,在教学过程中,如何设计有效的数学问题值得我们经常思索,以下笔者就这个问题谈谈自己一些肤浅的看法。
能有效促进学生发展的数学问题才是有效的数学问题,而类比型问题和探究型问题能有效地提高学生的学习能力;开放型问题和动态型问题能有效提高学生的思维水平。因此,在课堂教学中,设计类比型、探究型、开放型问题是教师设计有效数学问题经常采用的途径。
一、通过设计类比型问题,培养学生的联想、归纳能力
数学知识具备很强的外扩性,而新扩知识经常与扩前知识有许多类似之处。记得在“一元二次方程的解法(1)”的备课中,对于“教完开平方法后,如何引出配方法?”我总感觉找不到有效的解决途径。最后只能按书本上的方法,给出方程x2=10x+16=0,然后提问:能用因式分解或开平方法解吗?你能转化成(x+a)2=b的形式吗?引导学生用开平方法解。但是,我感觉这样的问题设计使得学生对于开平方法和配方法共性的认识很被动。后来,在一次听课过程中,我大受启发,该教师的问题设计有效地解决了我的困惑[2][3]。

图1
问题1:如图,上述四个图形能否拼成一个大正方形?(很多拼法:如图1)问题2:若大正方形的面积为121,能否列出一元二次方程?学生得到两个不同形式的一元二次方程:(x+3)2=121①;x2+6x+9=121 ②
问题3:你喜欢解哪个方程?(学生选择用直接开平方法解第①个方程)
问题4:那第②个方程该如何解?(学生回答:转化成①的形式然后求解)
该教师在问题的设计中渗透数形结合的思想方法,把同一个方程的两种不同形式放在一起进行类比,学生很自然地联想到旧知,教师轻松地导出了配方法。通过教师的精心设计,学生经历了知识产生的过程,主动认识到开平方法和配方法的关系,自发地对知识进行归纳和总结。因此,通过设计类比型问题,可以培养学生的联想、归纳能力。
二、通过设计探究型问题,培养学生的创新、实践能力
《数学课程标准》强调要“培养学生的创新意识、实践能力”。探索型问题要求学生自己搜集资料、自己观察、自己分析、自己总结。因此,教师设计探究型问题,可以引导学生积极思考,提高学生发现问题的创新能力和解决问题的实践能力[4]。
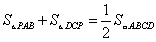
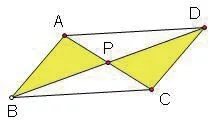
学生证明完毕后,教师再引导学生思考:
点P在其他位置上结论仍成立吗?
这就成为了一个很好的探究题。
探究问题1:若点P过一条对角线,而不过另一条对角线,结论是否仍成立?
探究问题2:若点P为平行四边形内任意一点,结论是否仍成立?
探究问题3:若点P在平行四边形的外部,结论是否仍成立?
学生在操作、观察、讨论、交流、归纳、猜想、分析和整理的过程中,理解了数学问题的提出、数学概念的形成、数学结论的获得与验证。设计探究型问题,其实质上是让学生学习科学研究的思维方式和研究方法,从而培养学生主动探究、获取知识、解决问题的能力。学生在主动探索知识的过程中培养了创新意识;在运用知识解决问题的实践活动中发展了实践能力。
三、通过设计开放型问题,培养学生积极、发散的思维
新课改要求,教师在教学中对不同的学生要作不同的要求,学生可以根据自己的情况有选择性、有目的性地学习。因此,教师设计的数学问题,要能促进不同层次的学生都能在原有基础上进一步发展与提高。设计开放性的问题,达到了为更多学生提供思考和表现机会的目的,激发了不同层次学生思维的活跃性[5]。
记得以前在一元二次方程解法的复习课上,我直接给学生几个一元二次方程,然后让学生采用合适的方法来求解方程。但是,这样的教学方式不但打击了学生思维的积极性和活跃度,还禁锢了学生的思维,使学生永远跳不出教师的“五指山”。思考之后,我重新设计了一个开放性题目:在下面的3个方框内填上你喜欢的数,编出一个一元二次方程:
□x2+□x+□=0
用你认为最合适的方法来解你所编的一元二次方程,请将结果与大家分享。
这个例题通过让学生填上自己喜欢的数,体现了学生的自主性。学生填的数很多,可以得到许多不同的一元二次方程。由于它们的难易程度不同,因此每个学生都有表现自己的机会,通过他们积极的思考,每个学生都在原有的水平上对知识加深了理解,使思维得到了一定程度的发展。显然,这样的问题设计比原来的问题设计更加合理有效。
总之,数学问题是教学思维的动力,并为思维提供了方向。在课堂教学中,教师要不断地给学生提出新的数学问题,为更深入的数学思维活动提供动力,使数学思维活动持续不断地向前发展。但课堂教学不能误以为就是问题的罗列,数学教师也不能只追求课堂上一问一答的形式上的热热闹闹,而应该选择“有效”的问题,在“适当”的时候提出,这需要教师在设计问题的过程中不断思考。我想,若每位教师都能要求自己经常思考,那我们的教育定会呈现出一片春光明媚!

