HPM 视角下数学课堂生成性资源的应用
——以分式方程解法教学为例
□陈春涛
(中山市华侨中学,广东中山 442000)
在课堂教学中,常常出现一些不在教师预设范围内的被动型资源.例如,分式方程(人教版八年级下册)第一课时教学的课堂中,出现了一些不同于“去分母”的解法.面对这些生成性资源,教师需要思考:“学生为何这样做?”“应当怎样应用这些资源?”“学生的这些解答给教师的教学带来怎样的启示?”即在HPM(数学史与数学教育)的视角下,审视每一种被动型资源产生的根源,既对课堂上随机产生的被动型生成资源从更高的角度解读,又可针对性地开展教学预设,从知识技能与情感态度等方面促进主动性资源的生成.
一、生成性资源的产生与呈现

件,得900-150v=0且(30+v)(30-v)≠0.

以上5种解法都能得到正确的结果,这些解法对学生此前的学习经验有很好展示,但都不是课本要求的“去分母”解法.
二、生成性资源的成因与分析
(一)比例性质的干扰(解法1)


(二)完美解法的重现(解法2)

(三)先驱之误[3]45的警示(解法3)
解法3、4 都是在保留分式结构的层面上解决问题,并未将其转化为整式方程来解决,所以运算比去分母复杂,这是二者共性的缺点.解法4 与“去分母”一样可能产生增根,解法3则容易失根.

(四)几何代数的融合(解法5)
如果把解法5用图形的方式表示出来,就可以用图1来解释.

图1

这种解分式方程的方法叫作几何代数法.在《几何原本》第2 卷中有着丰富的几何代数内容,斐波那契在《计算之书》中曾频繁使用这种方法[3]292.解法5就是斐波那契在这本书中介绍的方法.
三、生成性资源的利用与改进
从前文的分析发现,学生的几种不同解法很有代表性,有3 种解法都与数学史有关,为保证学生能在课堂上呈现这些解法,或暴露更多的典型问题,可以设置以下变式练习.

【设计意图】目的是希望学生直接去分母解方程.因数据比较大,计算会比较麻烦,甚至会计算错误,进而反思得到“先将原式两边同时除以300”的简便算法.例题也应两边先同除以30后再计算,这体现数学“最优化”原则.
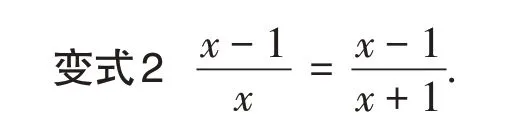
【设计意图】变式2 是针对解法3 而设计的,若学生根据“分式值相等且分子相等则分母相等”,将得到x=x+1,从而得出方程无解的错误结论.
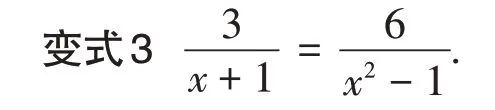
【设计意图】目的是希望学生错误地将两边同乘以(x+1)(x2-1),从而出现一元二次方程,再反思得到“去分母需要方程两边同乘以最简公分母”.同时,变式3 对于热衷于“交叉相乘”的学生也是极好的反例素材.
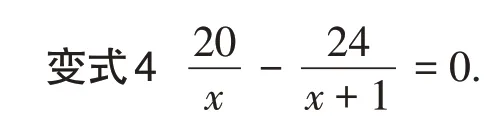
【设计意图】变式4 是将比例式移项的结果,意图通过学生的对比计算,体会到解法2的复杂运算和“去分母”的便捷.


变式6 如图2,已知点G,E,H,F 分别是矩形ABCD 边AB,CD 上的点,且GE=BE=CF=HF,已知S矩ABCD=90cm2,S矩AGHD=60cm2,AE=DF=30cm,求BE长.
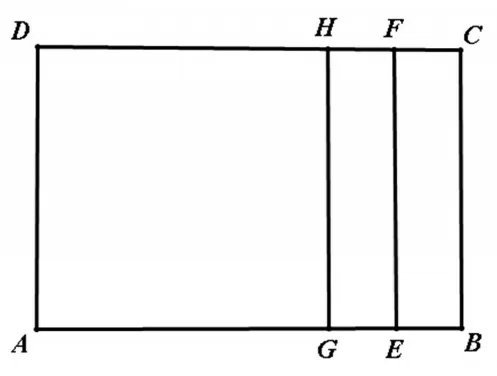
图2
【设计意图】几何代数法(即解法5)比较少见,课堂上不一定有学生呈现,故改为练习题.既可用之体现同一方程的不同实际背景,又可渗透对几何代数法解分式方程历史的介绍.
四、生成性资源的处理与思考
课堂上的生成性资源可分为被动型资源和主动型资源.被动型资源是课堂上由学生自主生成的、不在教师预设范围内的资源.对这种突发型生成性资源的应用极大地考验着教师的知识积累和教学智慧.主动型资源是教师根据教学经验,在备课过程中精心预设教学活动,学生在参与活动的过程中对应呈现的教学资源.HPM视角可以从更高的角度审视被动型资源,更合理地预设主动型资源.
(一)被动型资源的降维处理
1.面对问题应追根溯源
汪晓勤教授常说:“太阳底下没有新鲜事.”学生的许多错误都是历史上大数学家也犯过的错误,因此,对学生异乎寻常的解答,教师应首先追根溯源,既要了解这一知识是如何发展而来的,又要想清楚学生为何这样思考,从本源上找到原因,再相机引导,而不是单纯纠正学生的错误表象.
以解法5为例,若教师不明白用几何代数法解分式方程的历史,就会将其视为错误变形,反之,若能画出图1 来解释,学生对“数形结合”思想的理解就会深刻很多.
2.面对错误可将错就错
这就是苏格拉底的“产婆术”.当学生出现错误时,不直接纠错,而是引导学生用同样的方法解决其他问题,形成认知冲突,从而主动纠正错误.例如,对于应用解法3的学生,可以展示“桑德森之误”的解答过程,询问学生是否有误.此时学生自然会深入思考其中的原因,对应用等式性质、分式方程验根就会加深认识.
3.正确解答也借题发挥
对于一些并无错误的解答,教师也可强调注意事项,纠正书写规范,开展变式训练等.例如当学生用“交叉相乘”解方程时,教师可引导回顾比例的基本性质,再将比例的基本性质与等式的基本性质统一起来.学生用解法2解方程时,则可介绍费舍和施瓦特的“完美解法”.
4.问题较多当舍末逐本
课堂上学生可能呈现许多问题,此时教师应抓住当堂课的主体问题,淡化或后置其他问题.例如,分式方程的解法分为两个课时,第一课时主要体会“去分母”的优越性,第二课时才考虑增根的问题.所以在第一课时中,可不必出现会产生增根的分式方程.
(二)主动型资源的积极预设
在HPM 视角下,学生的很多错误都是历史上数学家曾经走过的弯路.与本课有关的数学史主要包含三个方面.(1)费舍和施瓦特的完美解法(解法2).(2)桑德森之误.桑德森是第一位将分式方程写入教材的数学家,他自幼失明却成为剑桥大学第四任卢卡斯教授,每天坚持上8 小时的课,被誉为“不用自己的双眼却教会他人如何使用双眼的人”.但就是这样一位伟大的数学家,也在分式方程求解的问题上犯了失根的错误,且没有意识到增根的问题[3]46.(3)用几何代数法解分式方程.历史上符号代数出现的时间非常晚,直到16 世纪法国数学家韦达才实现历史的突破,他在《分析引论》(1591)中使用字母表示未知数以及已知数[3]140,很多我们熟悉的代数公式当时都是用几何模型来解释的.
HPM 在课堂中可体现以下价值:揭示知识之谐、营造探究之乐、实现能力之助、彰显文化之魅、达成德育之效[4].以上涉及的历史有数学家的正确解法,学生从中可获得强烈的自信心;又有数学家的典型错误,可以缓解学生对数学的畏难情绪;还有用图形的方法解释解方程的过程,可以让学生感受数学思想的魅力.知识之谐、文化之魅、德育之效的价值都能实现,而这些正是数学情感态度目标的重要组成部分.
《义务教育数学课程标准(2011 年版)》对课程总目标从四个方面阐述:知识技能、数学思考、问题解决、情感态度[5],情感态度目标常被一线教师虚化,HPM 提供的丰富素材能让这一目标“实”起来.
所以,课堂预设除了知识技能层面的考虑外,还应从数学情感的层面去考虑.前面的变式练习中,变式1、3、5更多的是知识技能的层面预设,希望让学生体会到“去分母”的优越性;变式2、4、6的设置则是为了让学生能呈现出解法2、3、5,以便于渗透数学史,落实情感态度目标.
教学效果的达成有赖于教师的教学预设,但更依赖于学生的课堂生成.教学预设是教师给学生的考卷,HPM 视角下的这份考卷更成熟、严谨、充满智慧,学生需要认真分析、仔细解答、反思领悟;课堂上的生成性资源则是学生给教师准备的考卷,幼稚、杂乱、富含信息,教师却只能即兴发挥、顺势而为、概括提炼,这就是教给学生一碗水,教师需要准备一桶水的原因所在.HPM是值得我们去研究、汲取的资源.□◢

