高校学生评教结果有效性分析方法研究
——Z高校背景因素方差分析案例
梁志星,袁美玲
(1.中国民航大学,天津 300300;2.北京航空航天大学,北京 100083)
近年来,国家越来越重视本科教育教学的过程管理,重点是加强高校课堂教学建设并提高课堂教学质量。2018年教育部召开新时代全国高等学校本科教育工作会议,提出淘汰内容陈旧且轻松易过的“水课”,强调把教学质量作为教师考评的重要依据。国内高校已经探索实践了多种课堂教学质量评价方式方法,如督导评价、同行评价、管理人员评价、教师自评、学生评教等,其中学生评教是唯一一种能够实现课堂教学全过程覆盖、学生全员参与的课堂教学质量评价方式。在当前强调高校课堂教学质量大背景下,探讨高校学生评教非常有必要。
一、研究现状及问题
1.研究现状。从研究热度来看,对教学质量相关学术文献进行搜索统计可以发现,学生评教是其中的高频次、高中心性、高突现性关键词,是近年突现的研究热点。[1]从研究主题来看,关于学生评教主要分为支持派和质疑派,双方争议的焦点在于学生评教结果是否会受到背景因素的影响。针对背景因素对学生评教结果有效性的研究,近年来学术界采用了多种定量研究方法进行深度分析,主要包括以下几类:
一是采用回归分析方法,将背景因素与评教结果建立回归模型。如魏红等以北京师范大学学生对教师教学的总体评价得分作为因变量,以各项背景特征作为自变量,用逐步进入法进行多元线性回归分析[2];马莉萍等对某高校同一门课程学生评教数据建立混合回归模型,分析教师职称与学生评教之间的关系[3];戴璨等对湖北大学某学院学生评教数据进行实证研究,利用广义线性混合模型统计分析教师背景、班级属性和课程三大类非教学因素与评教分数的关系[4];李楠等采用抽样调查和调查问卷,引入logistic回归方法,测量学生成绩与学生评教行为之间的关系[5]。
二是采用因子分析方法,将背景因素作为评教结果的影响因素。马秀麟等利用聚类和主成分分析的方法,探究影响评教成绩的主要原因,认为“绝大多数的学生评教数据是客观的,能够比较真实地反映教师的教学状况,对教学的投入不足和实践性知识的欠缺是主因”[6];周继良等调查了江苏10所高校的学生,利用因子分析方法研究学生评教行为偏差影响因素,认为学科类别、学校类型、学生学业都会对学生评教行为产生影响[7]。
三是方差分析方法。李超锋等对某高校学生评教结果进行多因素方差分析,考察教师自身特征对学生评教结果影响的显著性,认为教师学历和年龄对学生评教结果具有交互效应[8];赵伟春等对浙江中医药大学某学院的评教数据进行单因素方差分析,结果显示“影响学生评教的主要非教学因素为课程类别、课程名称和学生年级”[9]。
2.问题提出。从研究现状来看,针对学生评教的定量研究取得了明显成效,实现了从纯粹理论推导到实证研究、从定性研究到定量研究、从问题研究到解决策略研究的转变。但是从实践来看,现有研究并没有消除高校学生评教有效性的质疑和争论,导致高校在实施学生评教过程中处于两难境地——一方面高校致力于持续改进课堂教学质量,另一方面却无法证明学生评教结果的有效性。在现实情境下,高校学生评教具有较强的差异性和持续的发展性,差异性表现在高校之间以及高校内部教师、学生、课程等方面,发展性则表现在随着时间轴延伸学生评教面临的背景因素也会发展变化。
基于上述背景及问题,现实情境的复杂性对学生评教分析提出了更高要求,开展学生评教的定量研究应注意四个方面:一是提取高校真实而全面的学生评教数据,采集全样本、全过程的大数据;二是注重分析方法的严谨性,运用成熟的统计方法理论推导出更科学、更可信的研究结论;三是实现数据结果的标准化和可比较性,为学生评教制度的持续改进提供量化依据;四是承认结论的多样性和发展性,如针对某一所高校的研究结论并不能推广到其他高校,同一所高校的结论也并不是一成不变的。为此,本研究以Z高校为案例,采用方差分析方法,分析学生评教结果与背景因素影响这一争议问题,尤其是强化了分析方法和分析过程的详细论证,为其他高校论证学生评教结果有效性提供可借鉴的经验。
二、单因素方差分析方法及过程:Z高校分析实例
质疑派通常认为教师、课程、学生三方面背景因素会影响或干扰学生评教结果[10],实践中高校管理部门和教师同样担心背景因素会干扰学生评教结果。深入分析背景因素对学生评教结果的影响程度,可以解答教师对学生评教结果有效性的质疑,同时也可以提升学校质量管理者对学生评教制度的信心,还可以根据分析结果找出学生评教结果的偏离影响因素并及时干预。通过对比多种定量分析方法,结合三类影响因素数据类型特征,本研究尝试采用单因素方差分析法(analysis of variance,简称ANOVA),以Z高校某一学期的学生评教截面数据作为分析实例。
1.选择变量。选择学生评教结果作为因变量(Y),评教结果是学生对课堂教学质量评价指标逐项打分形成的分数。提取Z高校某学期的学生评教原始数据(百分制),经过数据清洗及数据分类编码处理等环节,针对三类影响因素形成一一对应的三个因变量(表1):教师综合评价成绩Y1、课程综合评价成绩Y2、学生评教成绩Y3。Y1是指当学期每个教师名下所有选课学生评教成绩的算术平均数,数据量为984条;Y2是指当学期每门课程所有选课学生评教成绩的算术平均数,数据量为1 924条;Y3是指当学期每个学生对所有修读课程的评教成绩的算术平均数,数据量为19 161条。
选择背景因素作为自变量(X),背景因素指学生进行课堂教学质量评价过程中可能存在的潜在影响因素,主要包括教师、课程、学生自身的特征等,有的学者也将之称为“非教学影响因素”[11]。选取教师、课程、学生三大类背景因素作为自变量,结合Z高校实际情况选择17类具体背景因素作为自变量(表1),教师背景因素包括性别X1-1、年龄X1-2、入校年限X1-3、职称X1-4、最高学位X1-5、学缘X1-6、主持科研项目X1-7、发表论文X1-8、院系X1-9,课程背景因素包括课程性质X2-1、课程类别X2-2、课程学时X2-3、课程学分X2-4,学生背景因素包括性别X3-1、生源地X3-2、年级X3-3、学业成绩X3-4、当学期绩点X3-5。为实现分析方法的一致性,将自变量统一作为定类变量进行分组并进行数据编码处理(1,2,3,…,n)。
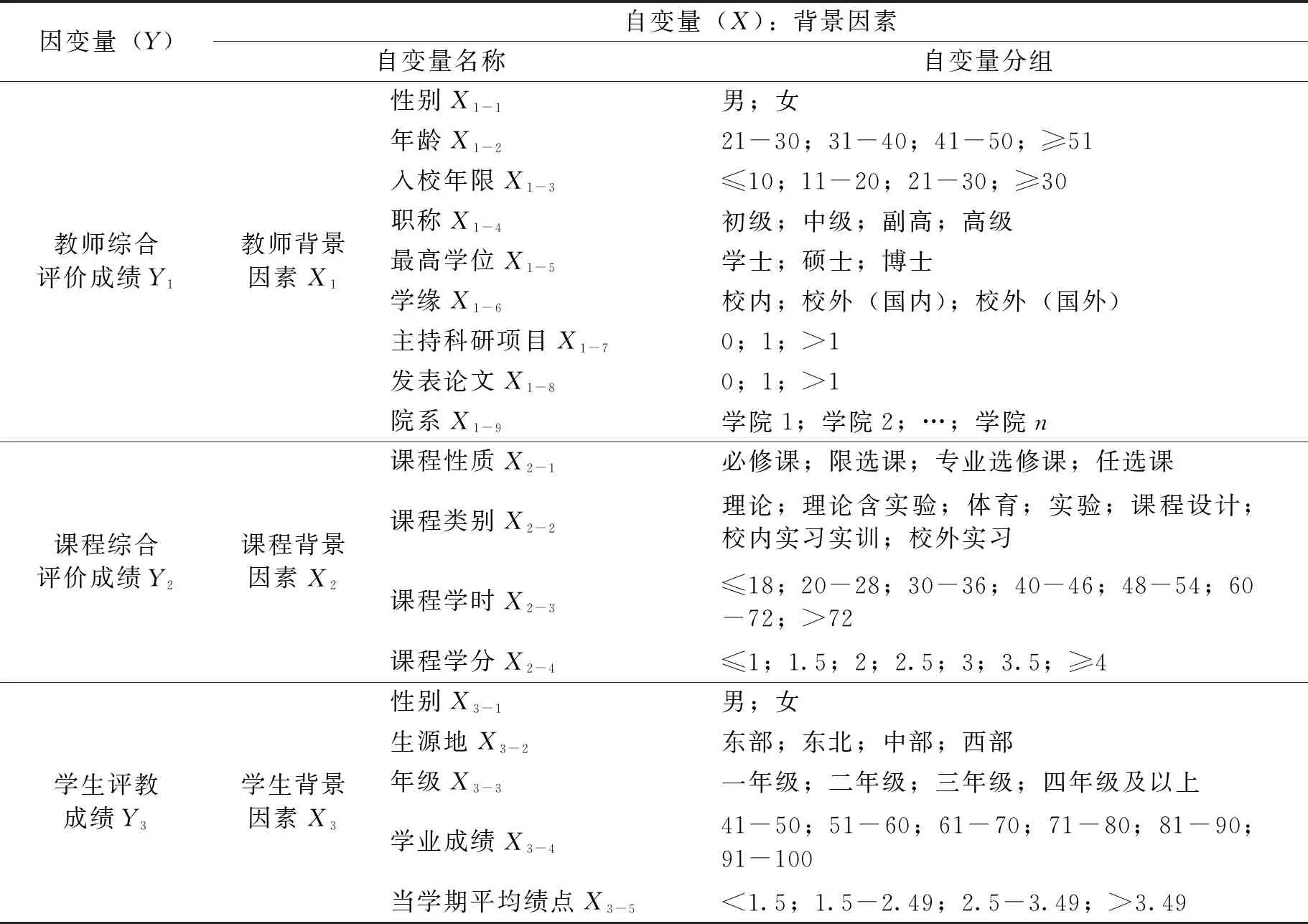
表1 Z高校学生评教分析因变量与自变量选择
2.统计过程。统计过程共包括五个步骤,具体见图1所示。
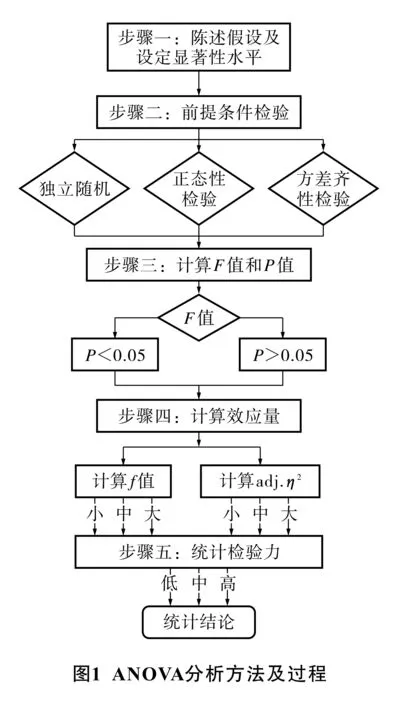
步骤一:陈述假设及设定显著性水平。
根据自变量分组情况设计零假设和备择假设(表1),零假设表述为根据自变量分组之后的因变量所有总体均数相同,见公式H0;备择假设表述为所有总体均数不全相同,即H0非真,见公式H1。以教师年龄为例,零假设H0为假设各个年龄阶段的教师综合评价成绩的总体均值相等;备择假设H1为各个年龄阶段的教师综合评价成绩的总体均值不完全相等。本研究采用社会科学领域常用的0.05作为显著水平临界值,如以教师年龄为例,当α<0.05时,表明不同年龄段的教师综合评价成绩存在统计学理论意义上的显著差异,当α>0.05时,表明不同年龄段的教师综合评价成绩不存在统计学理论意义上的显著差异。
H0:μ1=μ2=μ3=μ4=μ5…=μn
(1)
H1:μ1、μ2、μ3、μ4、μ5…μn不全相等
(2)
步骤二:前提条件检验。
使用单因素方差分析方法一般情况下需要满足三个条件假设:所有样本均采用独立随机抽样,所有分组的总体均呈现正态分布,所有分组的总体有相同的方差。条件假设一:本研究对Z高校学生评教数据进行的是全样本分析,满足随机抽样的条件,同时根据背景因素数据进行分组之后也保持了不同分组之间数据的独立性,因此满足独立随机抽样。条件假设二:根据现代统计学研究实践,如果高校学生评教数据量相对较大时,一般情况下就不需要再考虑正态分布的条件,当处理的是小样本的时候需要进行Kolmogorov-Smirno正态性检验。条件假设三:通过levene检验方法对不同分组的总体进行方差同质性检验,针对方差齐性检验问题,Cohen等人指出:“一个约定俗成的准则就是,如果最大样本量没有超过最小样本量2倍而且最大样本方差没有超过最小样本方差2倍,无需对方差齐性过于担心。”[12]数据结果显示,Z高校学生评教数据满足上述三个前提条件,可以适用方差分析法。
步骤三:计算F值和差异显著性概率P值。
R.A.Fisher爵士将方差分析定义为,“将总变异分解为由研究因素所造成的部分和由抽样误差所造成的部分,通过比较来自不同部分的变异,借助F分布做出统计推断”[13]。据此构造单因素方差分析基本结构表(表2),SSA反映各组总体样本均值之间的差异程度,又称组间离差平方和,这种差异是由随机误差和因变量(背景因素)共同造成;SSE反映随机误差大小,又称组内离差平方和,这种差异是由个体差异、因变量误差等不可解释的误差引起;SST反映全部数据总的误差程度,又称总离差平方和,SST为SSA和SSE之和。

表2 单因素方差分析基本结构表
为消除各组样本量多少对离差平方和大小的影响,需要将其平均化处理,即平方和除以自由度得到方差值MS。自由度是构成样本统计量的独立样本观测值的数目或自由变动的样本观测值的数目,用df表示,SSA的自由度为k-1,其中k为背景因素分组的个数;SST的自由度为n-1,其中n为全部样本量的个数;SSE的自由度为n-k。将组间方差MSA和组内方差MSE的比值F与给定的显著性水平α的临界值进行比较,做出对原假设H0的决策,当F值大于临界值时,显著性概率P值小于设定的显著性水平α,统计学认为这种情况下应判定拒绝零假设,表明根据自变量(背景因素)对因变量(评教结果)进行分组数据的差异具有统计学理论意义上的显著性。
步骤四:计算效应量。
显著性检验结果F值和显著性概率P值,解答了“自变量造成了因变量差异是否具有显著性”的理论意义问题,但是这种差异是否具有现实意义并不确定,同时未能解决差异强度、自变量与因变量之间的关联度问题。为了进一步分析背景因素对学生评教结果的差异强度和关联强度大小,同时提高统计结果的可信度,本研究引入了效应量概念。效应量可以认为是H0和H1之间距离的一种度量,它不依赖于样本大小,能反馈效应强度或者自变量和因变量的关联强度。[14]国内外关于效应量的计算方法各有不同,本文在差异强度方面和关联强度计算过程中均采用Cohen的算法。
一是关于差异强度测量方面,Cohen提出的关于独立样本t检验中的效应量(d)是学术界广泛认同的方法,他在此基础上又提出了关于单因素方差分析的效应量(f)的计算方法(公式3),其中k为分组数,F表示方差分析的F值,nk表示各组变量数值的调和平均数。效应量(f)取值区间为0~1,效应量越大取值越接近1,临界值为0.1(小效应)、0.25(中效应)、0.4(大效应)。
(3)
二是关于自变量和因变量之间的关联度测量方面,η2是一个常用的概念,由组间离差平方和(SSA)除以总离差平方和(SST)(公式4),胡竹菁等人认为η2作为方差分析后效果大小的指标意义比较好理解[15]。但是Cohen在其论著中认为“尽管η2是一个描述数据很好的统计量且对F值所提供的信息做了有价值的补充,但是η2主要的不足在于,它是对总体方差解释率的有偏估计”[12],为了提高研究的精确性,Cohen又进一步将方差统计量F值作为调节值,提出了修正后的方差解释率adjustedη2(简称adj.η2)(公式5),这与SPSS软件输出的adjustedR2完全一致。本文认为,方差解释率可以作为测量“背景因素”和“学生评教成绩”之间关联程度或回归程度的参考指标值。其取值范围和临界值,按照Christopher J. Ferguson总结归纳的社会科学领域的adjustedR2临界值,即0.04(小效应)、0.25(中效应)、0.64(大效应)。[16]
(4)
(5)
步骤五:计算统计检验力。
统计检验力是指“在虚无假设H0为假(备择假设H1为真)时,正确拒绝H0的概率”[17]。根据胡竹菁等人的建议,本文采用Cohen提出的单因素方差分析统计检验力的计算公式(公式6),其中f表示效应量,nk是各组人数的调和平均数,求出φ值,根据美国统计学会认可的方差分析检验力对照表[18],通过表中的组内自由度df和组数k,得出φ值对应的统计检验力。统计检验力取值区间为0~1,当P<0.05时,检验力越接近1表明检验结果可信度越强;当P>0.05同时效应量值表现为中等以上时,应当根据检验力值高低分情况采取后续的行动。[14]
(6)
3.数据结果分析。通过对Z高校某一学期的背景因素与学生评教结果进行单因素方差分析,形成最终分析数据结果(表3)。
(1)教师背景因素与学生评教结果。显著性概率(P)分析结果显示,随着年龄、性别、最高学位、院系的变化,教师综合评价成绩Y1的差异达到了统计学理论上的显著性水平(P<0.05);教师入校年限、职称、学缘、主持科研项目、发表论文的P>0.05,表明差异未达到显著性水平。
效应量(f)分析结果显示,院系对教师综合评价成绩Y1的方差效应量(f)为“大”,即f(0.415)>0.4,表明随着院系的变化,教师综合评价成绩Y1的差异达到了实际意义上的显著性水平;院系之外背景因素的效应量(f)均未达到中等水平,即f<0.25,表明随着院系之外教师背景因素变化,教师综合评价成绩Y1的差异未达到实际意义上的显著性水平。
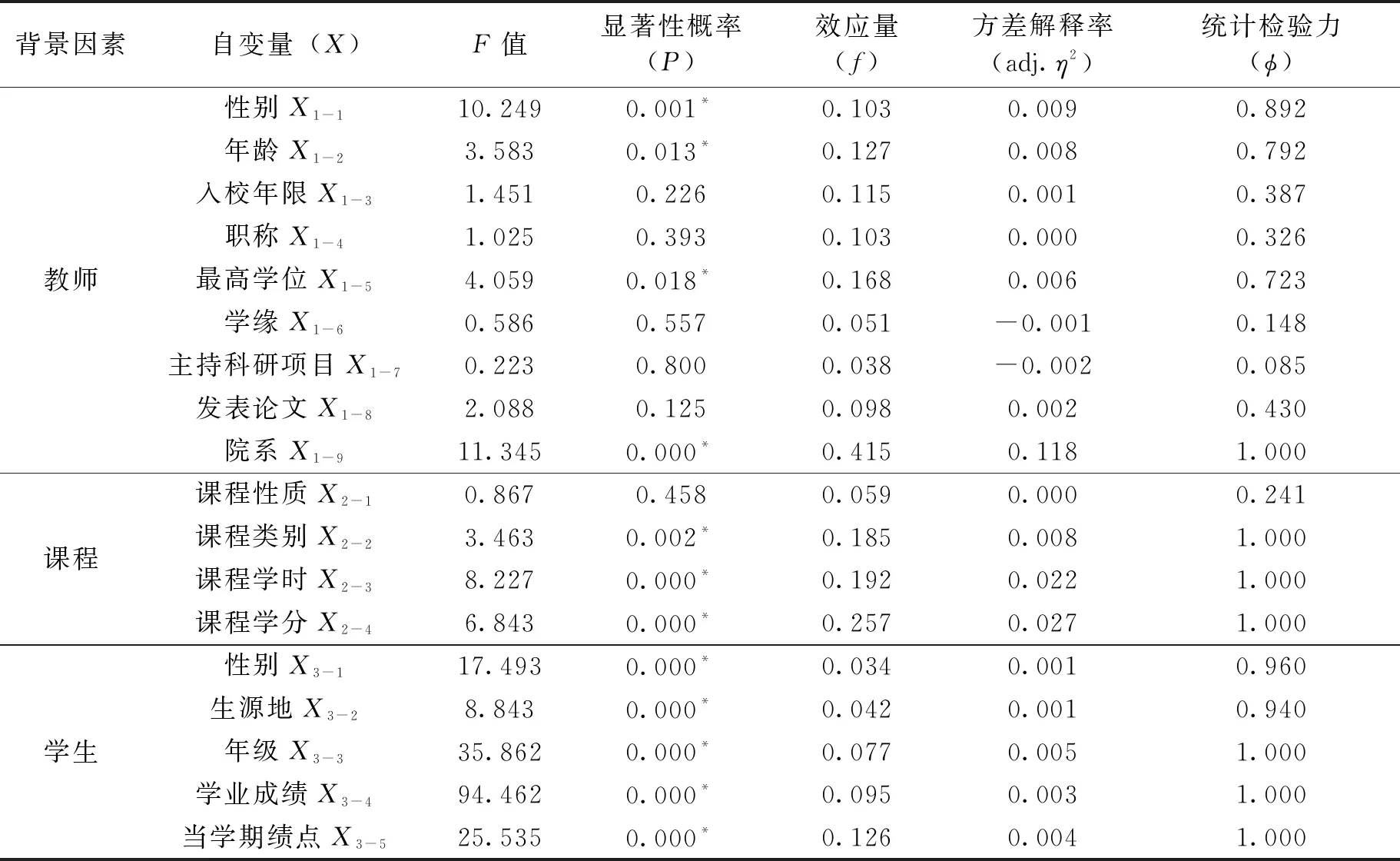
表3 背景因素与学生评教成绩单因素方差分析结果
方差解释率(adj.η2)分析结果显示,院系对教师综合评价成绩Y1方差的解释率为0.118,表明院系对于教师综合评价成绩Y1的方差贡献率达到11.8%,二者之间的关联度值得关注;除此之外,其他教师方面的背景因素方差解释率均低于最低水平0.04,表明关联度处于较低水平。
统计检验力结果表明,当P<0.05时,相应的统计检验力值均大于0.7,表明统计结果可信度较高;当P>0.05时,自变量的效应量值均表现为中等以下,统计检验力值不再考虑。
(2)课程背景因素与学生评教结果。显著性概率(P)分析结果显示,课程类别、学时、学分的P<0.05,表明随着这些因素的变化,课程综合评价成绩Y2的差异达到了统计学理论上的显著性水平;课程性质的P>0.05,表明差异未达到显著性水平。
效应量(f)分析结果显示,课程学分对课程综合评价成绩Y2差异的效应量(f)为“中”,即f(0.257)>0.25,表明随着课程学分的变化,课程综合评价成绩Y2的差异达到了实际意义上的显著性水平;学分之外的背景因素的效应量(f)均未达到中等水平0.25,表明随着课程性质、类别、学时变化,课程综合评价成绩Y2的差异未达到实际意义上的显著性水平。
方差解释率(adj.η2)分析结果显示,课程性质、类别、学时、学分对课程综合评价成绩Y2方差的解释率均未超过最低水平0.04,表明课程背景因素与课程综合评价成绩Y2之间的关联度处于较低水平。
统计检验力结果表明,当P<0.05时,相应的统计检验力值均接近1,表明统计结果可信度非常高;当P>0.05时,自变量的效应量值表现为中等以下,统计检验力值不再考虑。
(3)学生背景因素与学生评教结果。显著性概率(P)分析结果显示,学生四个方面背景因素P<0.05,表明随着性别、生源地、年级、学业成绩的变化,学生评教成绩Y3的差异均达到了统计学理论上的显著性水平。
效应量(f)分析结果显示,学生背景因素对学生评教成绩Y3的效应量(f)均未达到中等水平0.25,表明二者的差异未达到实际意义上的显著性水平。
方差解释率(adj.η2)分析结果显示,学生背景因素对学生评教成绩Y3方差的解释率均未超过最低水平0.04,表明二者之间的关联度处于较低水平。
统计检验力结果表明,学生背景因素与学生评教成绩Y3方差分析的统计检验力值均接近1,表明统计结果可信度非常高。
四、总结
通过ANOVA分析方法对Z高校某学期学生评教数据进行分析,不考虑其他因素干扰的前提下,可以初步得出如下结论:一是教师的院系不同,教师综合评价成绩Y1存在理论上和现实上的显著性差异,这种显著性差异的强度值为0.415,二者之间的关联强度值为0.118;二是课程的学分不同,课程综合评价成绩Y2存在理论上和现实上的显著性差异,这种显著性差异的强度值为0.257,二者之间的关联强度值为0.027;三是除了院系、学分之外,其他15个背景因素对学生评教结果的影响均不具有实际意义上的显著性或显著性效应微不足道,关联强度处于较低水平,即在不考虑其他因素的情况下这15个背景因素不会影响到学生评教结果。
提高教学质量离不开教学质量评价。“教学评价是一个动态的过程,教学效果的提升和改进也永远在路上,只有进行时,没有完成时。”[19]本研究还存在一些不足之处,如在自变量选取方面,只选取了高校内部的17个特征值作为自变量,未能穷尽所有的因素;采取了单因素ANOVA分析,对17类背景因素分别进行分析,这种方法不能反映出自变量之间的交互效应,现实过程中各自变量之间以及自变量与其他潜变量之间都可能存在复杂的关系,在后续研究过程中将探索引入新的分析方法,如多因素方差分析、结构方差模型分析等,以进一步提高对高校学生评教结果有效性的分析。

