如何提升学生的表达能力

王孝勤 李芳芳

[摘 要]表达能力作为一种基本素养，不仅可以加深学生对知识的理解，更能帮助学生深入学习，而且对于学生的人际交往和未来发展都有着深远的影响。小学阶段是培养学生表达能力的重要时期，表达能力的培养不应局限于课堂，而应贯穿于学习活动的始终。如何在数学教学中提升学生的表达能力，使学生想表达、敢表达、会表达，并做到言之有物、言之有理、言之有序、言之有力，是教育工作者要重点关注的问题。

[关键词]言之有物;言之有理;言之有序;言之有力;表達能力

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）11-0076-02

儿童时期是培养一个人表达能力的最佳时期，如果能在这一时期对学生的表达能力进行一定的培养和训练，让学生的表达有内容、有逻辑、有顺序、有感染力和说服力，那么学生未来的表达能力必定会非常高。

在课堂上，学生在表达时经常会出现无话、无条理以及无说服力的情况，面对这些情况，教师应该怎么做呢？

一、让学生从言之无物到言之有物

1.前置问题，改变学习顺序

课堂上经常会出现教师提出问题后，没有学生举手回答的现象，是因为学生不知道该怎么回答，还是学生根本就不会？反观课下，学生总是滔滔不绝说个不停。我想，课堂上学生沉默可能是因为他们不知道说什么，更不知道怎样去表达。如果我们能把问题放在课前，给学生充足的时间进行思考和交流，等到了课堂上，学生的表达必定是深刻的，也必定会言之有物。

例如，在教学“两位数乘两位数”前，我发给学生一张“预习单”，让学生带着问题去预习。

通过课前发“预习单”的方式，使得学生有充足的时间进行思考，并把自己的想法记录下来。学生用三种方法计算出14×12的结果。第一种是用点子图先算14×10=140，再算14×2=28，最后把两个乘积相加140+28=168。第二种是画长方形，学生通过图形看出要求14×12的结果就是求这个长方形的面积，然后把这个长方形分成两个小长方形，分别求出小长方形的面积再相加，算出14×12=168。第三种是把12变成3×4，也就是把算式14×12变成14×3×4，先算14×3=42，再算42×4=168。课前预习给了学生充足的时间思考，当学生思考出多种算法并能很好地理解算法时，在课堂上的表现必然是积极的，表达必然是言之有物的。

2.开放问题，优化学习支架

常规的提问方式一般是教师问一句学生答一句，并不能很好地锻炼学生的表达能力，学生的回答也是言之无物的。如果教师换一种方式提问，使问题更具开放性，给学生更多思考的机会，我相信学生的表达能力必然会有所提升。

例如，在教学“认识小数”时，学生按部就班地完成教师布置的任务：先寻找生活中的小数，再说一说什么是小数，比较小数和分数的联系和区别，这并没有给学生自主思考的空间。但如果让学生用不同的方法表达0.3这个小数，学生可能会有几种不同的表达方法。

方法1：把一个长方形平均分成10份，涂上其中的3份就是0.3。

方法2：把一条线段平均分成10份，其中的3份就可以用0.3表示。

方法3：把面积是1平方分米的正方形平均分成100份，每一份就是1平方厘米，其中的30份可以表示0.3。

通过画一画、说一说，学生对分数的理解越来越深刻，表达也必然是言之有物的。

二、让学生从言之无理到言之有理

数学既是一门讲道理的学科，又是一门有逻辑的学科，数学中的所有结论都不是凭空而来的，而是通过推理、抽象、概括等方式推导来的，那么，学生表达时怎样才能做到言之有理呢？

1.理解算法，说清算理

有些学生计算能力很强，却不知道为什么这样算，因为这些学生对算法掌握得很熟练，却不理解算理，这就使得他们在讲述计算过程时只能说出计算的方法，却说不出算理。

如果教师在教学中加强算理相关的训练，多问一些“为什么”，学生的表达定能从言之无理变成言之有理。

例如，在教学“两位数乘两位数”时，教师要引导学生多说说14×12的算理，让学生知道28表示2个一乘14是28个一，140表示14乘1个十是14个十，14的4应该写在十位上，1应该写在百位上。

学生通过说一说、练一练加深了对算理的理解，做到不光“知其然”还“知其所以然”，在表达时更能言之有理。

2.结合数学现象说清原理

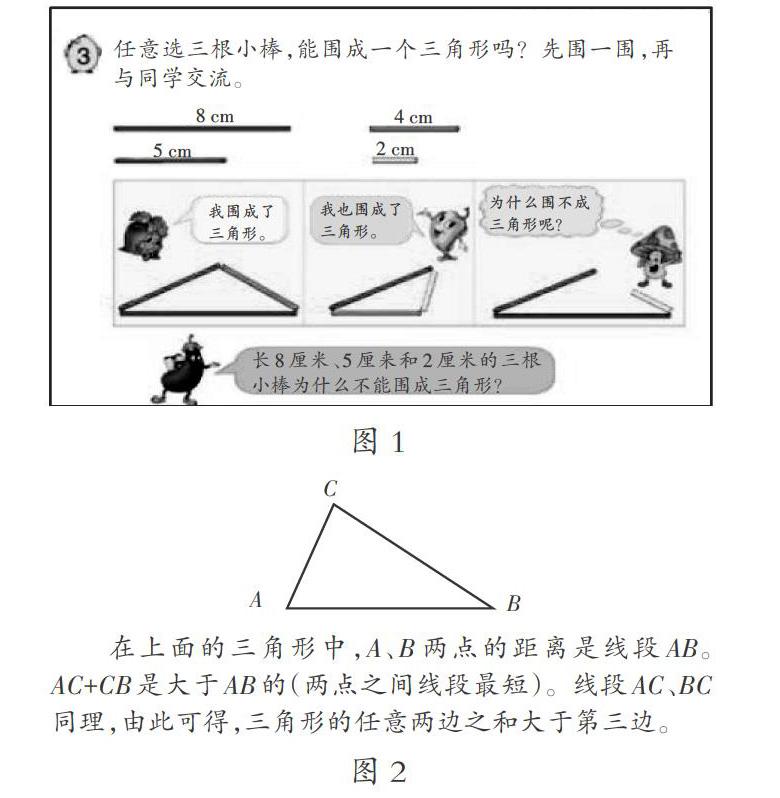
在解释“三角形的两边之和大于第三边”时，课本中运用了不完全归纳法推出结论：三角形任意两条边长度的和大于第三边长度（如图1所示）。但是学生对此并不能信服。为了让学生更清楚背后的原理，我画出一个三角形ABC（如图2所示），并透过图示的数学现象帮助学生说清算理。

三、让学生从言之无序到言之有序

有条理的语言可以让人更清晰地表达出自己的观点和想法，让别人更容易理解。学生在刚开始表达自己的观点时可能有很多话要说，但是并不知道该如何有条理地表达出来，别人听后仍然会感觉很困惑，这样的表达是言之无序的。

如果教师能够教给学生一些表达结构，学生就可以清楚、有序地表达自己的观点。比如告诉学生可以按照结构顺序，用“第一……第二……第三……”等词连接，或者按照时间顺序，用“先……再……然后……”等词连接，还可以按照程度顺序，用“首先……其次……再次……”等词连接，等等。

例如，在教学“长方形和正方形周长”时有这样一道题：

刘奶奶打算用篱笆围出一块长方形菜地，菜地长14米、宽12米，一侧靠墙，最少需要多长的篱笆？

一开始学生的表达是这样的：由题可知菜地的形状是长方形，长方形的长是14米，宽是12米，所以这个长方形可能是12米的那条边靠墙，这样篱笆的长就是其他三条边的长加起来，篱笆的长是14+12+14=40（米），因为长方形的长是14米，宽是12米，有一边靠墙，所以篱笆的长不是这个长方形的周长，也就不能用（14+12）×2来算，要减掉一条边，我们上面用的是12米的边靠墙，还可以用14米的边靠墙，如果是14米的边靠墙，篱笆的长就是14+12+12=38（米）。又因为题目中让我们求的是篱笆最少是多长，所以通过上面的计算得篱笆最少是38米。

随后我让其他学生分析这位学生的表述，大部分学生表示没有听明白。于是我又让该学生使用“第一……第二……第三……”这样的词，并重新组织语言进行讲解，下面是该学生整理后的回答。

我认为这道题目应该从以下三方面解决：第一，这块长方形菜地有两种围法，分别是长方形菜地的一条长边靠墙或一条宽边靠墙;第二，如果是一条长边靠墙，那么篱笆的长就是14+12+12=38（米），如果是一条宽边靠墙，那么篱笆的长就是14+14+12=40（米）;第三，题目中要求的是“篱笆最少多长”，那么答案应该是14+12+12=38（米）。

通过对比我们不难发现，把想说的话分成一、二、三点，会使表达更有序，别人就会更容易理解。

四、让学生从言之无力到言之有力

没有行动的语言是苍白的，只有借助一定的工具才会使语言更有说服力。教师在课堂上要经常使用举例、画图等方式来增加说服力，并让学生进行模仿。

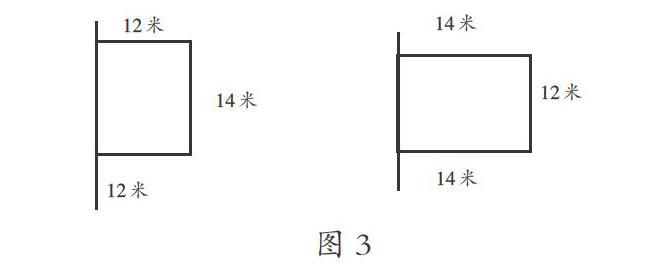
如前文这道题，当用画图的方式进行讲解时，学生就非常容易理解（如图3所示）。

通过图示可以清楚地看到：想要一侧靠墙围出一块长14米、宽12米的长方形菜地，有两种方法，一种是长方形的一条长靠墙，一种是长方形的一条宽靠墙，显然当长方形的长靠墙时所需的篱笆最少，因此最少需要篱笆14+12+12=38（米）。

举例也是经常使用到的教学方式，如在教学“乘法分配律”时，可以让学生用举例子的方法来验证（a+b）×c = a×c+b×c的正确性。判断“两位数乘两位数的积一定是四位数”是否正确时，可以举例10×11的积是一个三位数，从而判断出此题是错误的，再让学生举其他例子。通过举例可以使定理更具有说服力，从而使个人的表达从言之无力到言之有力。

数学课中的表达是一种思维的外在表现，提高学生的表达能力是一项细致的工程，在教学实践中，教师要不断摸索探究，并实施更多行之有效的训练方法和手段，带动学生表达，让学生有话可说、有理可依。教师在平时的教学中要抓住每个契机，让学生每天改变一点点，长久的坚持定会提升学生的表达能力。

（责编 黄 露）