基于竞争路径选择的HOT车道费率优化模型

邵春福,甄 理,刘 兵,董春娇,骆冠良

(1.北京交通大学 综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044;2.武汉理工大学 交通学院, 武汉 430063)

尽管大力发展公共交通有利于缓解交通拥堵，但公交专用道大多利用现有机动车道改建，导致机动车路权被侵占，在道路资源有限的情况下，降低了整条道路的通行效率，而高承载率收费(High-occupancy/toll，HOT)车道由于具备促进合乘、降低机动车出行总量的优势，已成为成功的车道管理办法之一[1].HOT车道是指允许满足乘客数量要求的车辆免费通行，而低于乘客数量要求的车辆缴费通行的一种车道[2]，合理的收费水平可以在保障公交车运行效率的前提下，提升路网的通行效率，提高道路资源利用率[3].因此，确定科学合理的HOT车道收费标准，是确保HOT车道实施效率的关键问题之一.

目前HOT车道的收费方式主要分为静态和动态两类，研究表明动态定价方案缓堵效果更优[4].动态费率制定的研究主要分为：①基于已投入运营HOT车道的实际数据获取出行者的支付意愿与合乘行为，以收费收入最大化、用户盈余最大化等为目标构建模型，得出最优收费策略[5].②通过建立模型或仿真模拟出行者的路径选择行为，计算出不同目标下的最优定价[6].由于我国尚未建成HOT车道，无法获得实际支付数据，因此第二种方法更适用于现阶段研究.Toledo等[7]对车辆到达和出行者是否选择HOT车道的过程进行仿真模拟，以确定动态通行费率；Boyles等[8]通过将出发时间选择与需求随机性结合起来构建了HOT车道收费算法评估方法；Laval等[9]运用不同定价策略实现最小总系统延迟，通过提高收费车道容量实现收益最大化.以上学者从不同角度对HOT车道费率进行研究，但多聚焦于在某条道路上设置HOT车道后一条道路交通状态、出行选择、交通效益的改变，而在实际出行中，出行者通常面临多条平行路径选择，在一条道路上设置HOT车道会对竞争路径的交通流造成扰动[10]，从而影响所有路径的交通流状态和用户效益，因此在实际建模中应考虑HOT车道对竞争路径的影响.范文博[11]提出HOT车道的实施方法为新建或占用既有车道，新建车道成本高昂且难以回收，占用既有车道会导致社会车道拥挤加剧，美国HOT车道多由HOV车道转化而来.我国公交专用道存在道路利用率不足的现状[12]，可考虑将其与HOT车道结合，通过制定合理费率在保障公交优先的前提下提升道路资源利用率.此外，目前HOT车道的研究主要集中在发达国家[13]，由于道路特性和居民观念等差异，在我国实施HOT车道更应考虑民众意愿及接受度，制定符合我国现状、合理有效的HOT车道收费方案.

综上，本文作者以公交专用道改建为HOT车道为背景，对存在竞争路径情况下出行者的出行特性进行分析，构建考虑竞争路径的出行选择行为模型并求解，获得实施HOT车道后原路径和竞争路径交通流状态的改变，然后结合原路径社会车道、HOT车道以及竞争路径的相互作用关系，以所有路径用户节约成本最大为优化目标构建费率优化模型，计算考虑全部出行者实际需求的HOT车道费率.最后以武汉长江隧道、武汉长江二桥和二七长江大桥为例，验证模型可行性，并对HOT车道进行效率评估，为在我国实施HOT车道提供借鉴和参考.

1 竞争路径下的出行者出行特性

为分析存在竞争路径时实施HOT车道后出行者的出行特性，对出行者进行意向调查.调查以具备过江需求的武汉市市民为对象，样本遵循随机抽样原则，将武汉长江隧道(GP1)、武汉长江二桥(GP2)和二七长江大桥(GP3)作为可选路径，GP2的公交专用道设置为HOT车道.问卷设置长距离、中距离、短距离3种情景，每种情景下设有原路径、HOT车道和竞争路径供被调查者选择.为选择HOT车道的被调查者提供节约时间为3、5、8和15 min的4种情景，每种情景下设置2～5元、5～8元、8～15元和15元以上4种费率水平.此次调查共回收有效问卷223份，统计结果如表1和表2所示.

表1和表2数据表明，随着出行距离增加，出行者选择HOT车道的意愿增强.同种费率下，节约时间越长出行者的支付意愿越强烈.HOT车道费率过低不利于保障其运行效率，费率过高会造成资源浪费.因此，HOT车道的定价应同时考虑车道服务水平和出行者的支付能力，将其控制在合理范围.

表1 不同出行距离下出行者选择各路径比例Tab.1 Proportion of travelers choosing each route under different travel distances %

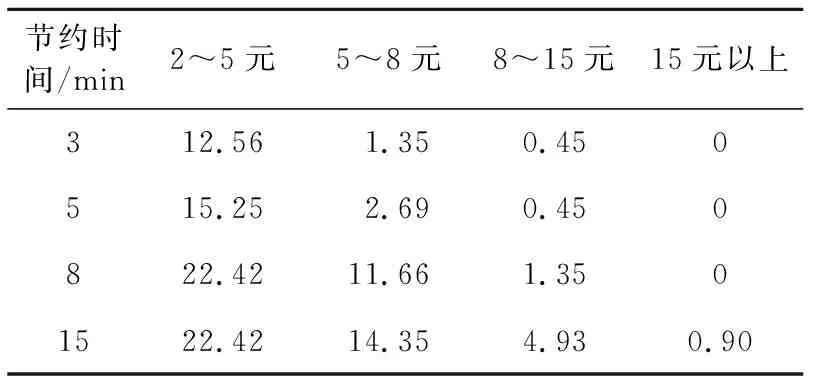
表2 不同节约时间下出行者的支付意愿比例Tab.2 Proportion of travelers’ willingness to pay for different time savings %

此外，问卷还对出行者的合乘意愿进行调查.设置HOT车道后选择合乘可用更低的成本使用HOT车道，节约出行时间.调查结果表明，选择HOT车道的出行者中，有50%接受两人合乘，40%接受3人合乘，30%接受四人合乘.合乘行为有助于降低交通流量，对缓解交通拥堵、提升道路利用率具有重要作用.

2 竞争路径下的出行路径选择模型

当存在竞争路径时，除原路径其他车道的车辆会转移到HOT车道行驶外，竞争路径的车辆也会因为节约时间而转移到HOT车道行驶，从而使整体路网的交通分布状态发生改变.出行者在选择路径过程中会考虑HOT车道的时间成本，当节约时间价值高于HOT车道费率时选择HOT车道，反之，选择社会车道.

在某一费率下，HOT车道节约的时间越长，出行者的支付意愿越强烈，支付意愿与费率呈负相关关系.因此，可建立函数关系

NHOT=f(ΔT)

(1)

τ=g(NHOT)

(2)

ΔT=tGP-tHOT

(3)

式中:NHOT为愿意选择HOT车道的出行者数量;ΔT为HOT车道节约的通行时间;τ为HOT车道费率;GP表示社会车道，tGP、tHOT分别为社会车道和HOT车道的行程时间.行程时间t根据美国联邦公路管理局提出的路阻函数(Bureau of Public Roads，BPR)确定[14].在计算HOT车道的行驶时间时，考虑到设计的HOT车道由公交专用道改建，其运行速度受公交车运行速度影响，零流时间应以公交车限速值为准代入计算.NHOT、ΔT、τ之间的大致关系如图1所示.

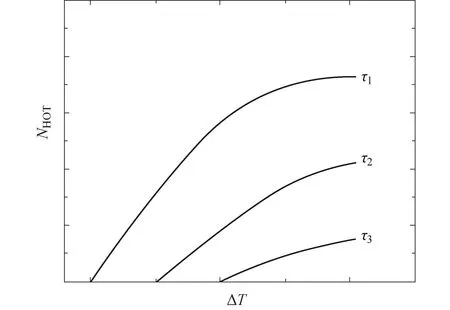
图1 不同费率下节约时间与支付意愿关系Fig.1 Relationship between time saving and willingness to pay under different charges

在图1中τ1、τ2、τ3为HOT车道的不同费率，且τ1<τ2<τ3.当费率为τ1时，随着HOT车道流量增多和节约时间增加，选择HOT车道的出行者数量随之增加.当费率为τ2时，由于费率提高，因此需要节约更多时间时，才开始有用户选择HOT车道，并且用户受到支付能力的限制，所能够支付的最大用户数量相较费率为τ1时有所减少.同理，当费率为τ3时，需要节约更多时间才有用户开始选择HOT车道，并且能够支付的用户最大数量减少.

出行者可选择社会车道和HOT车道，其出行方式可分为单乘与合乘两类，在某一费率下，将出行者分为缴费和免费两类人群，其定义如表3所示.

表3 缴费与免费人群定义

当费率为τ且节约时间为ΔT时，A1支付能力高于τ.接受合乘的人群中，A2支付能力介于τ与τ/2之间，A3支付能力介于τ/2与τ/3之间，B1支付能力低于τ/3.Pi为第i类人群数量占总人群数量比例，则有

PA1+PA2+PA3+PB1+PB2=1

(4)

在某一费率τ下，运用增量加载分配方法对车辆进行分配.初始分配时社会车道无车，因此无车辆选择HOT车道，车辆将驶入社会车道，第一次分配结束后，计算此时ΔT，若ΔT<0且NHOT<0，则继续按此比例分配，直至ΔT>0且NHOT>0时，有车辆驶入HOT车道，则不同类别的车辆数计算方式为

qA1=Ntotal×PA1

(5)

(6)

(7)

(8)

式中:qi为人群i的车流量;Ntotal为出行总人数;余数x、y、z为选择社会车道人数;P(τ，ΔT)、P(τ/2，ΔT)、P(τ/3，ΔT)分别为当费率为τ、τ/2、τ/3且节约时间为ΔT时选择HOT车道的人数比例;k2、k3分别为具有2人和3人合乘意愿的人数比例.

按式(4)～式(8)依次计算，最终可得到某一费率下各车道的车辆分配情况，输入不同费率进行求解，即可得到不同费率情况下各车道车辆分布情况，最终确定HOT车道流量qHOT与τ的关系如图2所示.

图2 HOT车道流量与费率关系Fig.2 Relationship between traffic flow and toll for HOT lanes

图2中qG为公交车流量(换算为标准车).当费率较低时，有支付能力的人数较多，此时HOT车道上车辆较多，随着费率逐渐增加，超出了部分人群的支付能力，HOT车道上车辆数随之减少，当费率继续增加至某一水平时，HOT车道上车辆类型为公交车和4人合乘车辆，因此曲线后半部分将趋近于直线qHOT=qB1+qG.

3 HOT车道费率优化模型

设置HOT车道可以提升道路通行效率，出行者可以节约行程时间和燃油费用，但也需支付通行费用，合理的费率应尽量保障设置HOT车道后用户成本节约Z最大.在未设置HOT车道时，所有出行者均需选择社会车道通行，其出行成本为时间价值成本和燃油成本之和；在设置HOT车道后，出行者选择HOT车道或社会车道出行，此时其出行成本为时间成本、燃油成本以及HOT车道通行费之和.用户成本节约为设置HOT车道前后用户出行成本的差值.将公交专用道设置为HOT车道后，为保障公交车运行效率，道路车流顺畅，其服务水平保持在b级以上[15]，即流量qHOT与密度CHOT的比值应小于等于0.7.由于设置HOT车道鼓励合乘，因此设置HOT车道后社会车道的服务水平会提升.据此，可构建非线性规划模型为

maxZ(τ)=

(T+B)-[T′(τ)+B′(τ)+R(τ)]=

ΔT(τ)+ΔB(τ)-R(τ)

(9)

s．t．

(10)

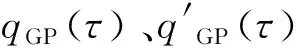
(11)

(12)

R(τ)=[qHOT(τ)-qB1(τ)]×τ

(13)

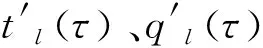
4 案例分析

4.1 算例求解

GP1、GP2、GP3分别为武汉长江隧道、武汉长江二桥和二七长江大桥的社会车道，经流量调查，qGP1∶qGP2∶qGP3=0.25∶0.4∶0.35.当节约时间ΔT>0时，PB1=0.3，k2=0.5，k3=0.4.武汉长江二桥限速60 km/h，公交专用道限速40 km/h.依据湖北省统计局数据[16]，湖北省人均年收入为55 071元，则工作日人均时间价值为24元/h.HOT车道(b级服务水平及以上)燃油单价为0.512元/km，高峰时段普通车道较拥堵，燃油单价为1.332元/km[17].

当总过江交通量为20 000 pcu/h时，将上述数据代入式(1)～式(8)，计算结果如表4所示.

表4 不同费率下各车道流量分布情况Tab.4 Traffic distribution of each lane under different tolls (pcu/h)

运用Matlab拟合表4中费用与各车道车辆流量变化曲线，得到此时q与τ的关系为

(14)

qGP1=109.42ln(τ)+4088.4，R2=0.96

(15)

qGP2=175.05ln(τ)+6541.0，R2=0.96

(16)

qGP3=153.26ln(τ)+5723.4，R2=0.96

(17)

式中：R2为拟合优度.将式(14)～式(17)中数据代入式(9)～式(13)进行计算，得到当总过江交通量为20 000 pcu/h时，HOT车道收费应为4.7元.

输入不同过江总交通量进行计算，即可得到HOT车道最优费率方案，结果如图3所示.

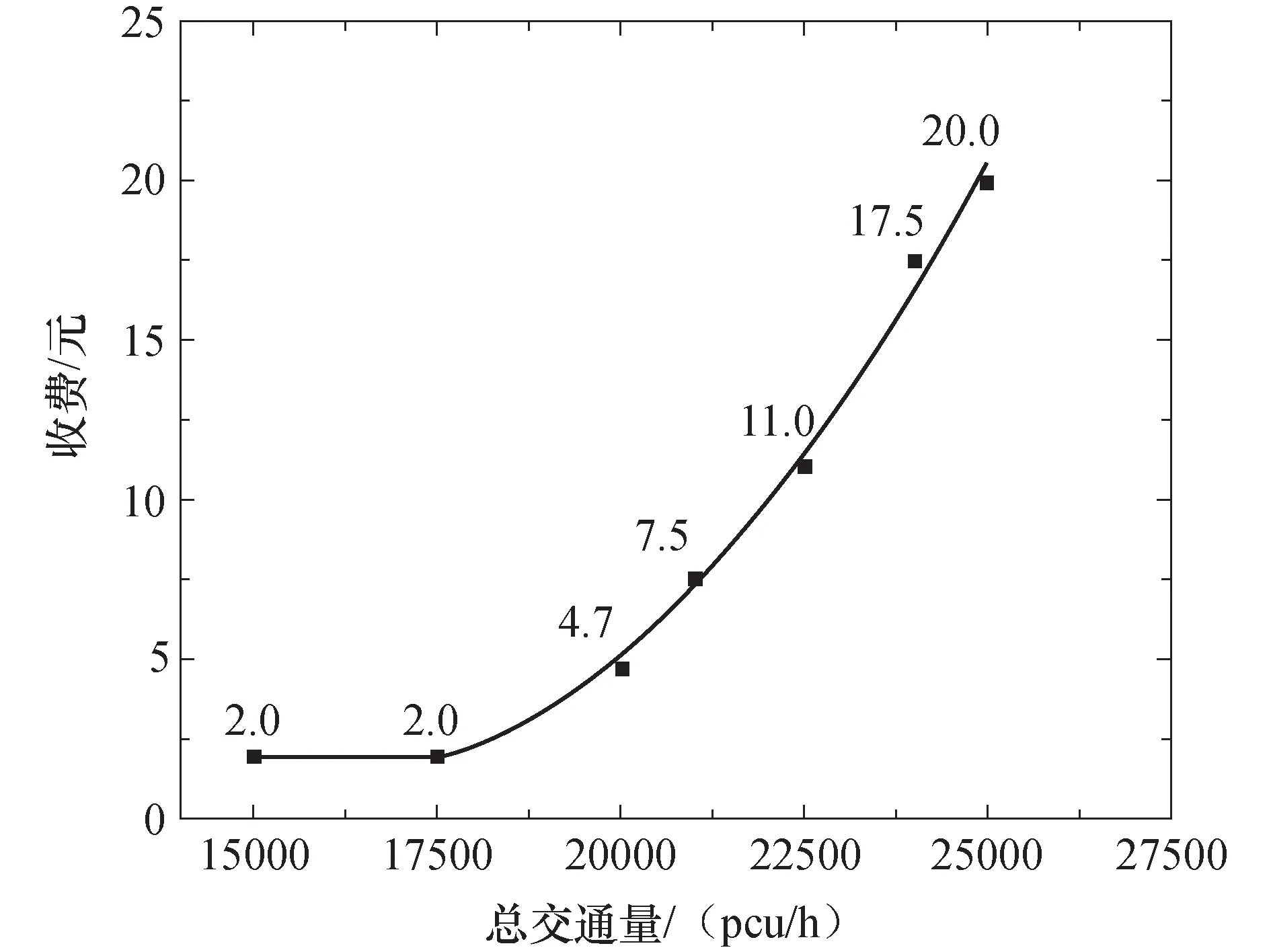
图3 不同总交通量情况下HOT车道最优费率Fig.3 Optimal toll of HOT lanes under different total traffic volumes

由图3可知，当总交通量小于17 500 pcu/h时，HOT车道与社会车道时间差值较小，此时选择HOT车道的人数较少，在任何费率情况下，均可满足约束条件，故当总交通量小于17 500 pcu/h时，取HOT车道的最低费率为2元/车，与公交车票价相同.

运用Matlab对图3所示图像及数据进行拟合，结果为

(18)

式中：qtotal为总过江交通量，根据式(18)可计算不同交通量下的最佳费率，实现HOT车道上费率的动态优化.

4.2 费率优化方案效果评估

根据多种总交通量下HOT车道的最优费率，可计算得到实施HOT车道后各路径流量变化情况如图4所示.实施HOT车道最优费率方案后，社会车道交通流量平均减少12.85%，总交通流量平均减少9%，说明HOT车道不仅分担了其他道路的交通流量，而且对合乘行为具有促进作用.

运用BPR函数对实施HOT车道前后各社会车道路径的行程时间和实施HOT车道后的降低延误进行计算，结果如表5所示.

由表5可知，实施HOT车道费率优化方案后，社会车道延误最大降低47.96%，最小降低25.87%，平均降低41.29%，交通量越大降低延误的效果越显著.故HOT车道在高峰时段所发挥的作用更显著，在实际应用中，可采取分时段开放HOT的措施，以更加合理有效地分配道路资源，提高通行效率.

图4 不同交通流量下实施HOT车道费率优化方案后路径流量变化Fig.4 Path flow variation after the implementation of toll optimization scheme for HOT lanes under different traffic flow

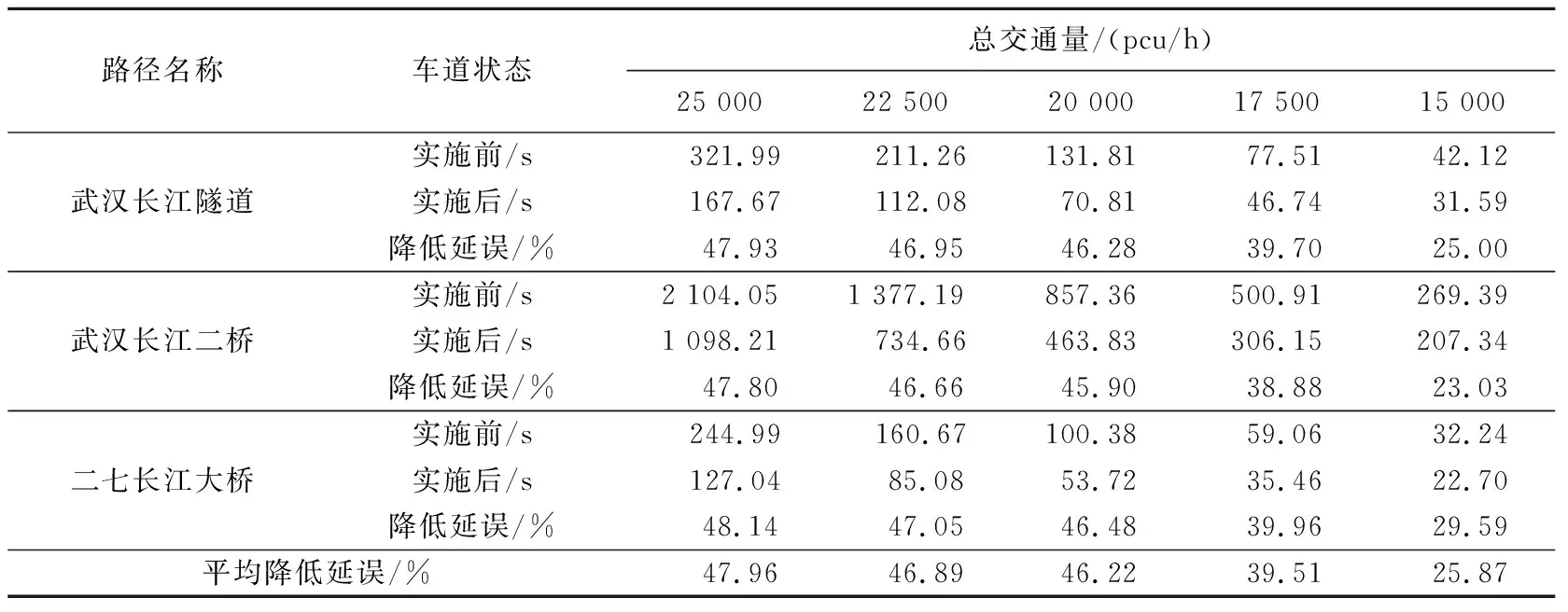
表5 不同交通流量下实施HOT车道费率优化方案后道路延误时间变化

5 结论

1)通过意向调查对存在竞争路径情况下出行者的出行特性进行分析，构建了考虑竞争路径的出行者路径选择模型，计算实施HOT车道后各路径的交通流量.

2)以设置HOT车道前后用户成本节约最大为目标函数构建了HOT车道费率动态优化模型，确定HOT车道最优费率.

3)以武汉长江隧道、武汉长江二桥和二七长江大桥为例，实现了动态最优费率计算，并对费率方案进行了效果评估.结果表明，优化的HOT车道费率方案能够减少9%的交通流量，降低41.29%的社会车道延误，实施HOT车道对促进合乘、降低延误、缓解周边路网交通拥堵具有良好效果.

4)由于路网结构的复杂性，出行方式的多元性以及出行选择行为的多变性，未来可进一步结合路网结构和出行方式，探索更多情景下出行者的路径选择行为，融合出行者时间价值的异质性计算最优费率，提升HOT车道的实施效果.