面向铁路夜间乘客疏散的定制公交线路优化

姚恩建,马斯玮,向 镇,高一迪

(北京交通大学 交通运输学院,北京 100044)

随着铁路运输系统的发展,夜间到站旅客数量急剧上升,乘客的疏散问题逐渐成为社会关注热点.定制公交通过集合个体出行需求,为出行起讫点、出行时间、服务水平需求相似的人群提供量身定制的辅助公交服务,具有较优的资源整合能力.政府及管理部门也于近几年陆续出台相关政策,促进客运定制服务的发展[1].针对铁路夜间到站乘客流量大、到站时间集中、目的地较分散的出行特征,线路灵活、快捷经济的定制公交对乘客的疏散具有极高的适用性.

定制公交的推广备受关注.Liu等[2]探讨了定制公交在中国的发展模式,对线路设计、时刻表编制等进行分析,阐述发展可行性.李彬[3]探讨了定制公交车型设置原则，并对定制公交线路设计和运营进行了理论探讨.Cao等[4]等通过RP、SP调查分析了人们对定制公交等出行方式选择的影响因素,对工作日定制公交的开行方案提供参考.在停靠站点设计方面,Qiu等[5]在需求不确定性环境下提出了动态可变站点策略,但对是否可将乘客需求点进行合并缺乏研究.邱果[6]在定制公交乘客的出行需求分布感知算法的基础上，提出了P-DN算法进行乘客出行需求起终点的聚类，但仅考虑了距离对聚类点的影响，未考虑如何实现所有乘客步行距离最小的聚类目标.在线路规划方面,胡郁葱等[7]提出了多起终点多车型混载的定制公交线路规划模型.李艳梅[8]利用层次分析法,建立了乘客需求可拆分的定制公交线网规划模型.姚恩建等[9]建立了同步优化发车间隔和车型配置的多目标优化模型，能实现公交企业的运营成本最小化，但主要针对的是常规公交.王健等[10]建立了以车辆运营里程最小为目标的车辆调度模型,但该模型由于将车辆延误带来的乘客时间价值损失转变为当量行驶里程,忽视了不同地区乘客时间价值的差异性.

综上而言,目前对定制公交的研究主要集中在通勤类定制公交的运营模式方面,对于集中到达的大客流疏散缺乏理论支撑,且在站点设置中对乘客总步行距离的考虑欠缺，在线路优化中对乘客时间价值成本的权衡方面研究不成熟,对保障乘客出行时间集约化的模型设计欠妥.本文作者充分考虑定制公交的服务水平,基于实时获取的乘客需求,采用改进的DBSCAN算法进行定制公交停靠站点聚类，并提出了兼顾乘客出行时间价值成本和公交运营成本的多线路动态规划算法.

1 模型构建

由于铁路夜间到站乘客的目的地类型较为单一，多集中于居住区域，存在对相邻目的地进行聚类的可行性.且由于铁路夜间到站乘客流量大，定制公交对集中到达的大客流疏散具有较高的适用性.为实现公交企业和乘客双方利益均衡,通过改进的DBSCAN算法进行聚类,并结合道路停靠条件确定停靠站点,以定制公交运营成本和乘客时间价值成本之和最小为目标,进行线路动态规划.

1.1 停靠站点的确定

充分考虑特殊乘客(如行李数量多、行走不便的乘客)对于门到门服务的需求,以及各目的地之间的相对位置,采用不受聚类点分布形状影响的DBSCAN算法作为基础算法,并在此基础上考虑乘客人数权重进行聚类分析.算法的核心参数为最小邻域点数MinPts和邻域半径EPS，MinPts为最小聚类乘客人数，EPS为乘客下车后的步行距离.

不同于传统DBSCAN算法所设定的聚类中心到达各个目的地几何距离之和最小,改进定制公交疏散方案考虑了乘客人数权重对总步行距离的影响,以期使得所有夜间乘客步行距离之和D达到最小,表示为

(1)

式中:ah为聚类簇内各点到聚类中心的距离；nh为聚类簇内各点的乘客数；h为聚类簇内目的地的个数.

1.2 线路优化模型

1.2.1 优化目标

线路优化的目的是在兼顾企业运营成本的同时保障较高的服务水平.以定制公交运营成本和乘客出行成本之和最小为目标,建立线路动态规划模型.其中,定制公交运营成本Cs主要包括:固有成本(含维修成本)和燃油成本(与运距和载客量成正相关)，Cs的具体形式为

Cs=CbN+CfLb

(2)

式中:Cb为固有成本,元/车;Cf为单位里程的燃油成本,元/km;Lb为车辆运行里程,km;N为车辆数,辆.

乘客的出行成本包含票价和时间价值成本,其中,票价由乘客目的地位置决定,与定制公交线路规划结果无关,故不计在目标函数内.采用收益法[11]对乘客的单位时间价值成本V(元/min)进行评估,可以表示为

(3)

式中:Z为乘客年收入，元；∂取1.0～1.5，用于计算将乘车时间用于加班工作得到的报酬；t为一年中有效工作时间平均值，本文取2 032 h，即121 920 min.

因而由定制公交绕行产生的乘客总时间价值成本Cp可以表示为

Cp=V×ΔT

(4)

式中:ΔT为定制公交绕行延误时间,min.

改进定制公交线路规划方案将定制公交运营成本和乘客出行成本之和最小作为优化目标，目标函数Z′可表示为

minZ′=Cb×N+Cf×

(5)

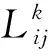
(6)

1.2.2 约束条件

线路优化模型的约束条件主要包括车辆的出发及到达时间、载客量及绕行距离的约束,以此保障较高的服务水平.

1)车辆的出发时间约束

定制公交车辆的发车时间由列车到站时间Tα确定,本文假设不同乘客的换乘步行时间相同,乘客异质性较小,故发车时间Td需满足

Tα+θ≤Td≤Tα+Tm

(7)

式中:θ为乘客步行到达定制公交发车点所需平均时间,min;Tm为乘客所能忍受的最长等待时间,min.

2)车辆的到达时间约束

定制公交车辆到达站点的时间早晚相对于出租车直达时间确定,因此定制公交到达站点i的时间Tbi应满足

Tti≤Tbi≤Tti+ΔT

(8)

式中:Tti为出租车直达站点i所需时间(含乘客等车时间)，min.

乘客对延误时间的容忍度与乘客到站点的远近有关,一般而言,到站点越远的乘客对延误时间的容忍度越高,反之越低.问卷调查数据表明(有效问卷328份,调查人群男女比例1.25∶1),85.7%的被调查者可接受的绕行延误时间上线为20 min,因此ΔT=20 min.

3)载客量约束

定制公交的乘客人数应小于核载人数，表示为

(9)

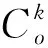
4)绕行距离约束

定制公交从站点i经过站点r到达站点j的行驶距离应不大于从站点i直达站点j的距离乘以自由线网的非直线系数ω，表示为

(10)

1.2.3 求解算法

首先采用启发式插入算法,通过将目的地插入路径集合的方式获得路径的初始解,其次采用遗传算法对初始解进行优化.遗传算法中采用自然数编码,利用片段交叉和基因兑换的交叉变异方式进行迭代,并将模型的目标函数作为适应度函数.

由于模型目标函数保障了乘客出行时间成本之和最小,因此规划结果受到不同站点下车人数权重的影响.假设存在3个停靠站点A、B、C，三者位置见图1.

图1 乘客人数权重对线路规划结果的影响Fig.1 Impact of passengers’ number weight on route planning results

定制公交车辆从站点A出发，在不考虑人数权重时，依据最短路原则应首先到达站点B，然后到达站点C，即此时的线路为A→B→C.而在考虑人数权重的情况下，假设在站点C的下车人数远大于在站点B的下车人数,即此时从站点A→C与A→B的乘客时间成本之差大于A→C与A→B的燃油成本之差，即

Cp×(ΔTC×WC-ΔTB×WB)>

Cf×(LAC-LAB)

(11)

此时，乘客的时间价值成本起主导作用，路径选择将由最短路选择方案(A→B→C)改为考虑人数权重的选择方案(A→C→B).

2 案例分析

依托北京南站所在的西南区域随机选取40个目的地、100名乘客进行验证.同时获取各目的地的位置坐标、乘客人数等. 考虑到铁路夜间到达乘客的目的地多为居住区域，目的地的选取多为人口密集的居住区.

2.1 模型求解

采用DBSCAN聚类确定停靠站点,考虑到乘客步行半径要求,设置MinPts=2,EPS=500 m.聚类结果如图2所示.不同的形状代表不同类别，点状为单独成一类的停靠站点，共有四类.将聚类所得四个质心点(聚类点1～4)选取在交通便利、利于车辆停靠的地方,其余不满足EPS约束的目的地直接加入停靠站点集合，在地图上进行标注，见图3.

图2 聚类结果图Fig.2 Clustering results diagram

图3 各站点实际位置Fig.3 Location of each stop on the map

图4 线路规划结果示意图Fig.4 Schematic diagram of route planning results

表1 线路信息

2.2 结果评价

为充分证明模型的有效性,将改进定制公交疏散方案与出租车疏散方案、传统定制公交疏散方案进行对比.

2.2.1 与出租车疏散方案的对比分析

定制公交及出租车到达各个停靠点所需时间以及车载乘客的总出行时间如表2所示.其中出租车出行时间为行程时间与打车等待时间之和,根据文献[13]定义打车时间为30 min.

定制公交疏散效率E的提高比率可表示为

(12)

式中:λc为乘客乘坐出租车出行总时间,min;λb为乘客乘坐定制公交出行总时间,min.

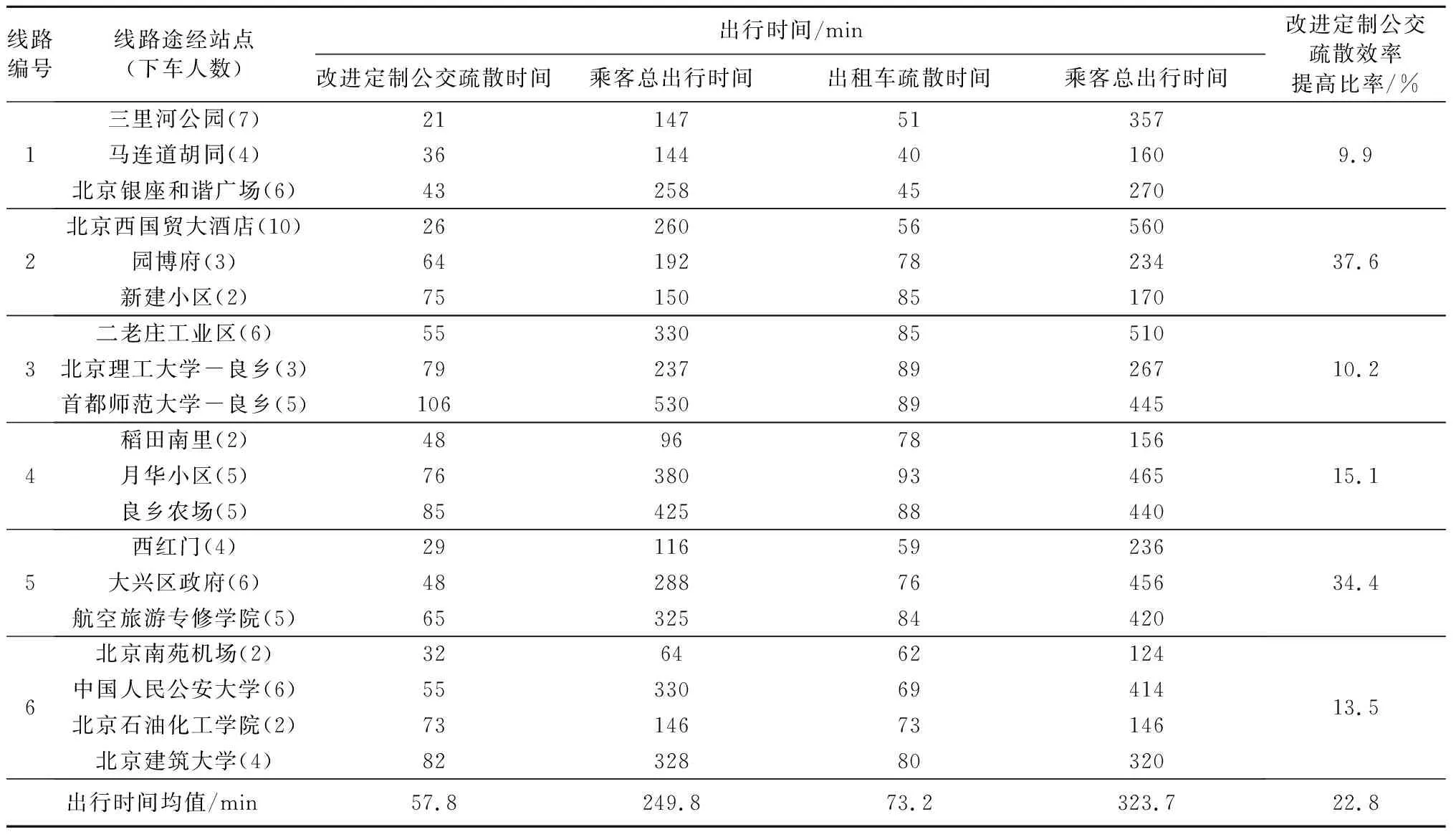
表2 改进定制公交疏散方案与出租车疏散方案对比

由表2可知,尽管改进定制公交疏散方案中，存在某些站点定制公交到达的时刻晚于出租车直达时刻，但从乘客总出行时间的角度而言，各线路的定制公交疏散效率均有所提高，提高比率为10%～35%,均值20.1%,标准差0.125,有理由认为本文先聚类后线路规划的线路优化模式具有较高的疏散效率.

2.2.2 与传统定制公交的对比分析

为模拟传统定制公交的运营模式,本文不再进行停靠点聚类,并删除目标函数(式(5))中对乘客时间价值的计算,其余约束条件与本文模型一致.因此，传统定制公交线路规划方案将定制公交运营成本最小作为优化目标，目标函数Z″可表示为

(13)

求解结果显示,采用传统定制公交运营模式对相同数量、相同目的地的乘客进行疏散,共需开行7条线路.

1)运营成本对比

将改进定制公交疏散方案与传统定制公交疏散方案所需车辆数、运营总里程及运营成本进行对比,如表3所示.

表3 改进定制公交与传统定制公交疏散方案的运营成本对比

可以看出,针对同一的疏散任务,改进定制公交疏散方案所需车辆数较传统定制公交疏散方案减少,可节省14.3%的固定成本和17.4%的燃油成本,总运营成本下降26.9%,利于企业的可持续发展.

2)疏散效率对比

将改进定制公交疏散方案与传统定制公交疏散方案中车辆到达各个停靠站点所需时间及车载乘客的总出行时间进行对比,公交运行时间为实际路网下运行时间(由百度地图计算得到),如表4所示.

由表4可知,在40个站点、100名乘客中,有27个站点、64名乘客的出行时间缩短、出行效率提高,占停靠站点总数的67.5%,乘客总数的64%.不同线路的乘客出行时间缩短幅度有所差异，其中线路3的各个站点发乘客出行时间均有一定缩短，优化效果最为理想.整体而言，乘客出行总时间的均值与传统定制公交相比缩短10%.可见本文提出的疏散方案能有效提高乘客疏散效率,在改善传统定制公交的运营效果和服务水平方面卓有成效.

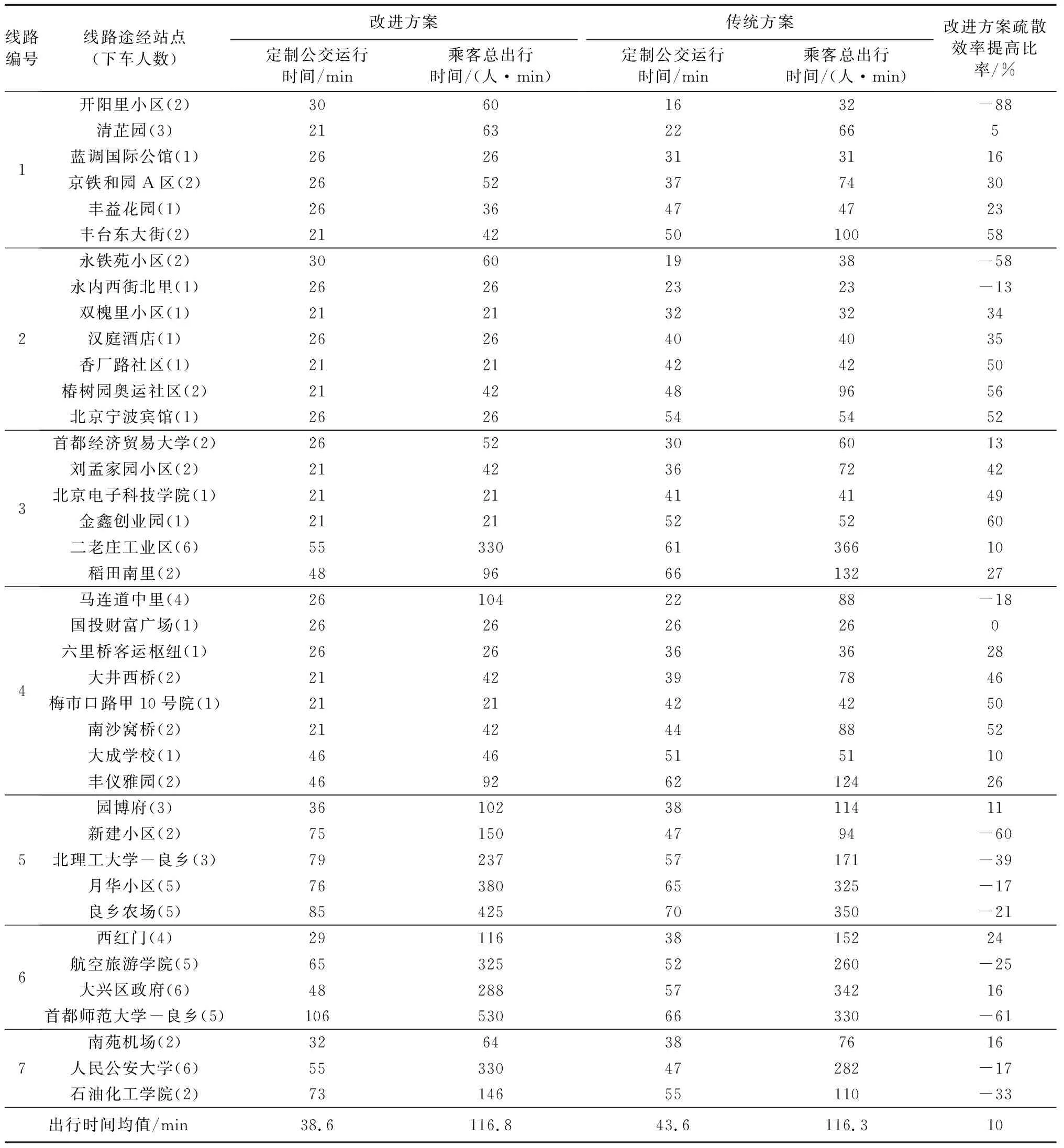
表4 改进定制公交与传统定制公交的疏散效率对比

3 结论

1)在充分考虑乘客的出行时间成本和公交企业运营成本的基础上，建立了以公交服务水平为目标函数的线路优化模型.案例分析结果表明,本文提出的疏散方案与出租车相比,可提高10%～35%的疏散效率,相比于传统定制公交,可节省26.9%的运营成本,缩短10%的出行时间.

2)通过定制公交解决集中大客流的疏散难题,有利于提高出行质量,促进便捷、共享交通出行方式的发展,对于解决夜间有大批量乘客到达而缺乏配套交通服务系统的铁路车站、机场等所存在的乘客疏散问题有重要的借鉴意义.