以实践操作促进学生自主学习

【摘要】本文以《圆的面积》的教学为例,论述以实践操作促进学生自主学习的途径,建议教师重视学生的学习主体地位,在课堂上引領学生开展自主探索、实践操作,进而深入理解“转化”的数学思想方法。
【关键词】小学数学 自主学习 实践操作 转化思想
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2021)05-0115-03
在小学阶段,《圆的面积》是学生学习平面图形面积的最后一个内容。经过前面阶段的学习,学生已经积累了关于平面图形面积的知识,初步理解了可运用转化的数学思想方法进行平面图形面积的计算。在日常教学实践中,大部分教师通过课件演示引导学生进行归纳、比较,得出圆的面积计算公式。很显然,这样教学忽视了学生的自主探索和自主操作,导致学生仅熟记圆的面积计算公式,而不知道这个计算公式是如何产生的。笔者认为,教师应让学生借助操作展开自主探索,引导学生运用圆的面积公式解决简单的实际问题。有基于此,笔者尝试从学生的自主探索入手,开展如下教学实践活动。
一、课前学情分析
在实施课堂教学之前,笔者在班级中进行了知识前测,前测内容包括对圆面积的认识、对圆面积的计算两个方面。其中,对圆面积的计算方面有三个层次的测试:调查学生是怎么解决的,是怎么知道圆面积的计算方法的,以及是怎样推导出圆的面积计算公式的。笔者借助这三个层次的学情测验,充分了解学生已经掌握的圆的面积计算知识有多少,以及认知渠道来自哪里。
根据学前测试,笔者对学生的学习起点进行了分析和研究,主要包括以下几个方面:
第一,基础知识。学前测验显示,有73%的学生能够完全理解圆的面积的意义,并且可以通过动手测量得出相关的数据,再通过面积计算得出圆的面积。这说明大部分学生已经对圆的面积的计算方法有了初步的认识。
第二,基本技能。有49.5%的学生可以通过动手操作,将圆剪拼成长方形或平行四边形,从而推导得出圆的面积计算公式。有15%的学生不会进行面积的推导,只会用自己的方法计算圆面积。
第三,基本活动经验。有少部分学生通过参与课外辅导,能够初步认识到要将圆转化成近似的长方形或平行四边形,但对掌握如何进行转化存在一定的困难。
第四,基本的思想方法。有52.5%的学生初步具有转化的数学思想方法,认识到可以运用转化进行面积推导。但仍旧有约40%的学生不知道要运用转化的思想方法进行面积学习。
综合以上学情,笔者认为,《圆的面积》一课的重要教学任务是帮助学生建立转化的数学思想方法。为此,需要教师调整已有的课堂教学策略,激活学生的转化经验。具体如何调整呢?笔者认为,教师可以进行两个方面的调整:
其一,教师可以借助以前学过的平行四边形、梯形等面积计算公式的推导,让学生通过回顾反思以激活和唤醒“转化”的数学经验,然后在此基础上,引导学生利用这些经验进行圆的面积计算公式的推导,从而深入理解和运用转化的数学思想方法。
其二,教师要给学生足够的空间和时间,带领学生进行自主操作,经历操作的动态过程,把圆剪拼成不同的图形,由此推导出圆的面积计算公式,通过这种自主操作感悟和理解推导面积计算的多样性,培养和发展学生的推理能力和数学思维能力。
二、教学实践
【教学片段一】
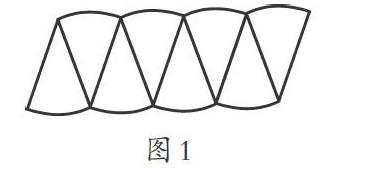
笔者先带领学生回顾推导平面图形面积计算时运用的转化方法,学生初步理解转化的数学思想方法,并动手操作,将圆转化为平行四边形或长方形。接着,笔者让学生分组进行操作,并向大家展示自己的操作过程,说一说自己是如何进行推理的。有学生将圆等分成8份,将这8份拼接起来,形成一个近似的平行四边形。(如图1所示)
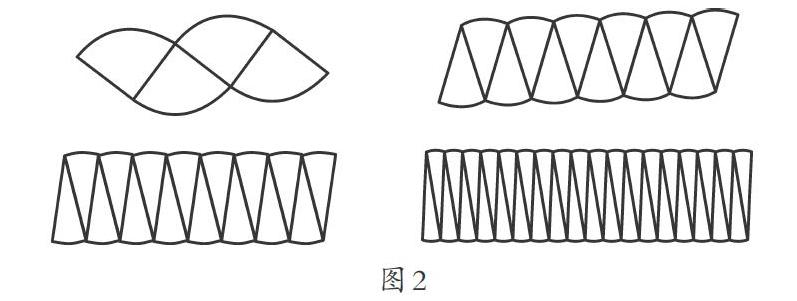
有学生把圆等分成4份、12份、16份、36份……然后拼接起来。(如图2所示)
学生经过操作后发现,等分的份数越多,拼接起来的图形越接近平行四边形(长方形)。学生将圆转化成平行四边形(长方形),根据平行四边形的面积计算公式为底边乘高,由此可以推导出圆的面积计算公式为[πr]2。(如图3所示)
【教学片段二】
笔者引导学生进行拓展性操作:除将圆转化为长方形和正方形,还可以转化为其他图形吗?请试一试。
有学生进行了如下尝试,将圆等分为8份,拼接成一个梯形。(如图4所示)
有学生将圆等分为9份,拼接成一个三角形。(如图5所示)
在拼接过程中,学生发现,将圆等分的份数进行拼接,不同的份数拼接出的结果是不一样的,拼成三角形要将圆等分的份数和拼成梯形要将圆等分的份数是不相同的。通过拓展性操作,学生成功地将圆转化成了三角形或梯形,并通过转化写出了圆面积计算公式的推导过程。
【教学片段三】
笔者引导学生思考:除了“把圆等分之后拼接,转化成熟悉的图形”的方法,你还有没有其他的方法推导得出圆的面积计算公式?
学生进行创造性操作。有学生提出把圆边等分成8份,只取其中一份,这一份就是一个近似的三角形,其中这个三角形的底边是圆周长的[18],高就是圆的半径,根据三角形的面积计算方法,就能够推导得出圆的面积计算公式。(如图6所示)
有学生将圆等分成8份,然后取出其中的4份,将其拼起来,拼成一个近似的三角形。(如图7所示)
以上教学环节,笔者通过三个层次的操作活动,引导学生对圆的面积计算公式推导展开自主探索,让学生经历了圆的面积计算公式推导的全过程,通过操作实践,提高了全面理解和应用数学思想方法的能力。
三、教学思考
通过《圆的面积》一课的教学实践,笔者对课堂教学实践有了更深入的思考。
(一)要充分发挥学生自主探索的积极性
学生在学习圆的面积的内容前,已经积累了一定的探索经验和探索知识,笔者通过学前测试对学生所掌握的知识进行分析,由此把握了学生对圆的面积计算方法的已有经验和知识,发现学生存在两个问题,一是只会运用计算公式,二是不会把圆转化成其他图形再进行推导。这说明学生缺乏自主探究圆的面积的能力,需要得到教师的积极引领。为此,笔者对课堂教学进行了策略调整,将重点放在了如何引导学生思考,带领学生尝试动手操作,将圆转化成其他图形进行面积公式推导。在此过程中,学生不断地发现、不断地探索出新的成果:将圆转化成三角形、梯形、长方形、正方形等。这让每一名学生都有机会进行自主探索,进而提高学习的能力。在数学课堂教学中,让学生积极参与课堂探究,是培养学生数学学习能力的有效途径。
(二)要给学生足够的时间经历概念形成的过程
《义务教育数学课程标准》(2011年版)明确指出,要让学生经历观察实验、猜想、推理等活动过程,培养和发展学生的数学思维。也就是说,学生在学习数学概念、计算公式、数学理论时,需要经历概念计算公式推导形成的过程,这是学生理解抽象概念必须经历的感性积累过程。然而在教学实践中,教师往往为了赶进度,而忽略了学生对概念认知的感性积累,导致学生知其然不知其所以然,其探究能力、推理能力、数学思维能力无法实现提升。在《圆的面积》一课的教学实践中,笔者给学生提供了近40分钟的课堂探究时间,让学生有足够的时间进行探索,一边尝试一边思考,从中发现和感悟,最终获得推导圆的面积计算公式的经验。在这个过程中,学生积累了数学活动经验,其探究能力也有了长足的进步,同时对数学学习也有了较强的自信心。
(三)要将数学思想方法的渗透贯穿教学活动
在小学数学教学中,数学思想方法的渗透不可或缺。然而数学思想方法具有一定的抽象性,是对数学事实和理论经过概括后的本质认识。这就需要教师设计有效的、具体的教学活动,让学生通过教学活动过程对数学思想方法进行感悟,在感悟中获得体会,并逐步构建数学思想方法。在《圆的面积》一课教学中,笔者主要向学生进行了两个数学思想方法的渗透,一个是极限思想,另一个是转化思想。极限思想的渗透是通过学生将圆等分成4份、12份、32份等,拼接成近似的平行四边形,通过这个操作活动让学生进行想象:如果一直等分下去,结果会怎么样?借助这个直观操作和想象的活动过程,学生很容易体会和理解极限思想。转化思想的渗透是在学生已有的学习平面图形面积的基础上,带领学生展开操作,将圆顺利转化成平行四边形、长方形、三角形等已经学过的图形,由此推导出圆的面积计算公式。在这个过程中,学生还能够运用转化的思想,创造性地选取了圆的一部分进行圆的面积计算公式推导。很显然,这表明学生对转化思想有了深入的理解,最终转化成了精准的应用。
【参考文献】
[1]谢珠英.转变学习方式 深度学习数学[J].课程教育研究,2019(6)
[2]陈金太.精准把握发力点,构建高效数学课堂[J].小学数学教育,2019(5)
[3]毛亚峰.借助操作,深化“转化”思想——“圆的面积”教学实践与思考[J].小學教学参考,2019(14)
[4]陈应芬.用转化思想促学习深入——从“圆的面积计算公式推导”教学为例[J].小学教学参考,2020(2)
[5]荀步章.创设“问题场”引发“思维流”——《圆的面积》教学实践与思考[J].教育实践与研究(A),2011(11)
作者简介:谭晓云(1978— ),女,广西兴业人,大学本科学历,一级教师,主要研究方向为小学数学教学。
(责编 雷 靖)

