管束式换热器流动换热的非线性现象研究

王文洁，凌玲

（1-奥克斯空调股份有限公司，浙江宁波 315100；2-宁波水表股份有限公司，浙江宁波 315000）

0 引言

在众多物理现象中，如弹性系统、范德波尔方程和人口增长简单模型等，其动力学特性往往需要用非线性方程来表示。这些非线性方程通常没有解析解，但可通过计算机及相应的算法来求得其数值解[1-2]。非线性系统的解的形式有多种：稳定定态解、发散解和振荡解。稳定定态解即各参数不随时间的变化而变化；发散解就是无解，通常没有意义；振荡解分为周期性振荡解和混沌，周期性振荡解即解随着时间呈现周期性变化，而混沌解无固定规律[3]。关于换热器设计优化[4-8]、流动换热[9-13]前人已有较多研究，但管束式换热器流动换热系统作为非线性系统，其特性几乎很少有人关注。本文主要是通过仿真技术模拟展示该特性并以此解释烟可视化实验中遇到的流动非对称现象。

杨茉等[14]采用SIMPLE算法，QUICK差分方案，对封闭方腔内水平板自然对流换热的非线性特性进行了数值模拟研究。杨伟等[15]采用数值模拟及实验的方法对底部加热的复合多孔介质热流耦合传热过程进行了数值求解和温度测试，在小Ra工况下，确定了非线性分叉、震荡解的特征值。付超等[16]采用实验及数值模拟方法，对两层多孔介质内热流耦合对流传热解的特性进行了研究，计算了不同材料比例下的流体分叉、震荡等实际临界瑞利数。雍青青等[17]通过引用周期性边界条件将模型简化,通过数值模拟技术考察了不同雷诺数下流体横掠管束的流场和温度场。郑建城等[18]通过数值计算研究了封闭圆内开缝圆自然对流的非线性特性。

通常认为在流体横掠管束的流通通道内，流动与传热是对称分布的，但随着Re的增大，其流场与温度场逐渐转变为振荡，而后转变为混沌。由于实验无法准确描述该现象，本文使用Fluent软件对管束内的流动与传热进行数值模拟，从而对管束空间内的非线性特性进行分析。

1 物理模型

横掠管束对流换热的局部流动通道如图1所示，图(a)为三维流动换热，顺排管束布置，考虑三维巨大计算量，将问题简化为二维来模拟计算。模型如图(b)所示，纵向管间距记为Sn，横向管间距记为Sp，换热管外径d为30 mm，通道的几何尺寸关于水平中心线完全对称[19]。

图1 横掠管束x对流换热的局部流动通道

2 数学描述

流动介质为水，通道内水的进口质量流量为m（kg/s），管壁设为恒壁温。假设问题为二维、非稳态、不可压缩、常物性，忽略黏性耗散，不考虑重力作用，出口符合局部单向化假设。

不可压流体流动换热的无量纲方程：

以上无量纲参数定义：

式中，τ为时间变量，s；uin为来流平均速度，m/s；u为x方向流体分速度，v为y方向流体分速度，m/s；ρ为流体密度，kg/m3；p为流体压力，Pa；T为流体温度，K；TW为管壁温度，K；Tb(x)为横坐标x的截面上流体平均温度，K；ν为运动黏度，m2/s；α为导温系数，m2/s。

取x流动方向3个圆管周期为计算域（图1(b)），给出周期性边界条件如下[19]：

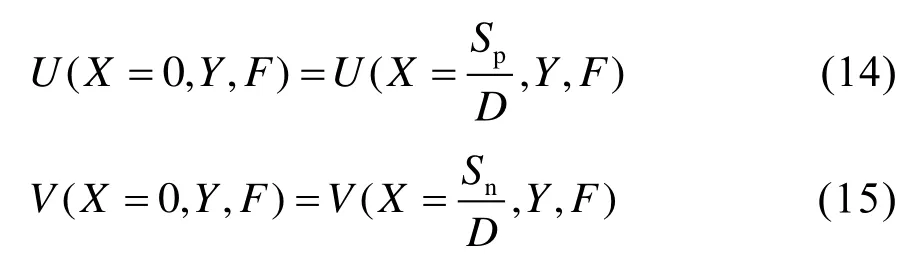
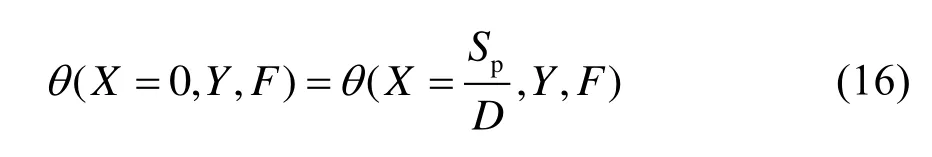
y方向对称性边界条件为：

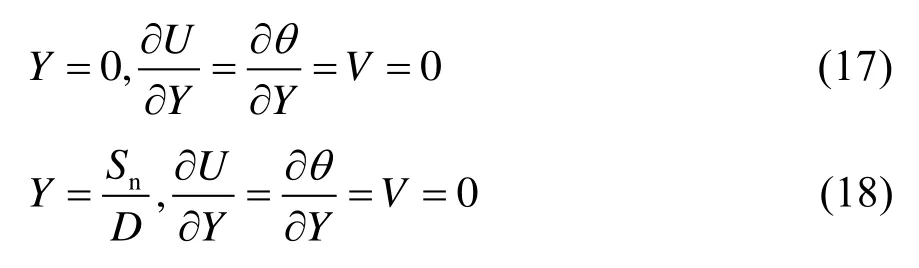
对计算域内部圆管附加条件：

问题是非稳态的，因此给出初始条件如下：

因为初始计算条件对最终数值稳态计算结果无影响，所以最终数值稳态计算在进行一段时间后才被认为进行至稳态。

3 数值方法

使用ANSYS FLUENT软件对非稳态横掠顺排管束的流动与换热进行模拟计算，流动方向上用周期性边界条件，竖直方向上用对称性边界条件，换热管为无滑移恒温壁。采用SIMPLE方法处理压力速度耦合[20]，对流扩散项用二阶迎风格式，采用可实现化k-ε方程模型进行湍流模拟计算。并对圆管表面进行验证，满足壁面增强函数要求。

以管间距Sp/d=Sn/d=1.06的布置方式为例，计算网格数为49 781，节点数为25 338。首先验证网格独立性，对不同网格数模型进行数值模拟，结果如表1，当网格数达到23 000时，网格数对数值计算结果已无影响[20]。

表1 不同网格数的平均Nu

4 计算结果及分析

4.1 管束空间内的非对称现象

4.1.1 不同Re的速度场

以管间距为Sp/d×Sn/d=3×3的管束为例，如图2所示，主流方向为周期性边界条件，竖直方向为对称边界条件[21]，管壁为恒温无滑移固体壁面，流动介质为水，对不同Re下的流场与温度场进行数值模拟，设置速度监测点1。

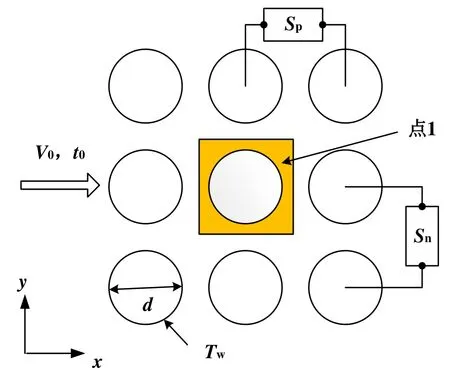
图2 计算模型

图3所示为不同Re下监测点point-1的速度相图。由图3可知，在低Re下，流场为稳定定态解，监测点速度不随时间的变化而变化，如图3(a)；当Re增大时，速度相图逐渐从单个周期转变到倍周期，流场随时间呈周期性变化，其中图3(b)为1倍周期，图3(c)为2倍周期；若Re继续增大，流场便进入了混沌状态，如图3(d)。

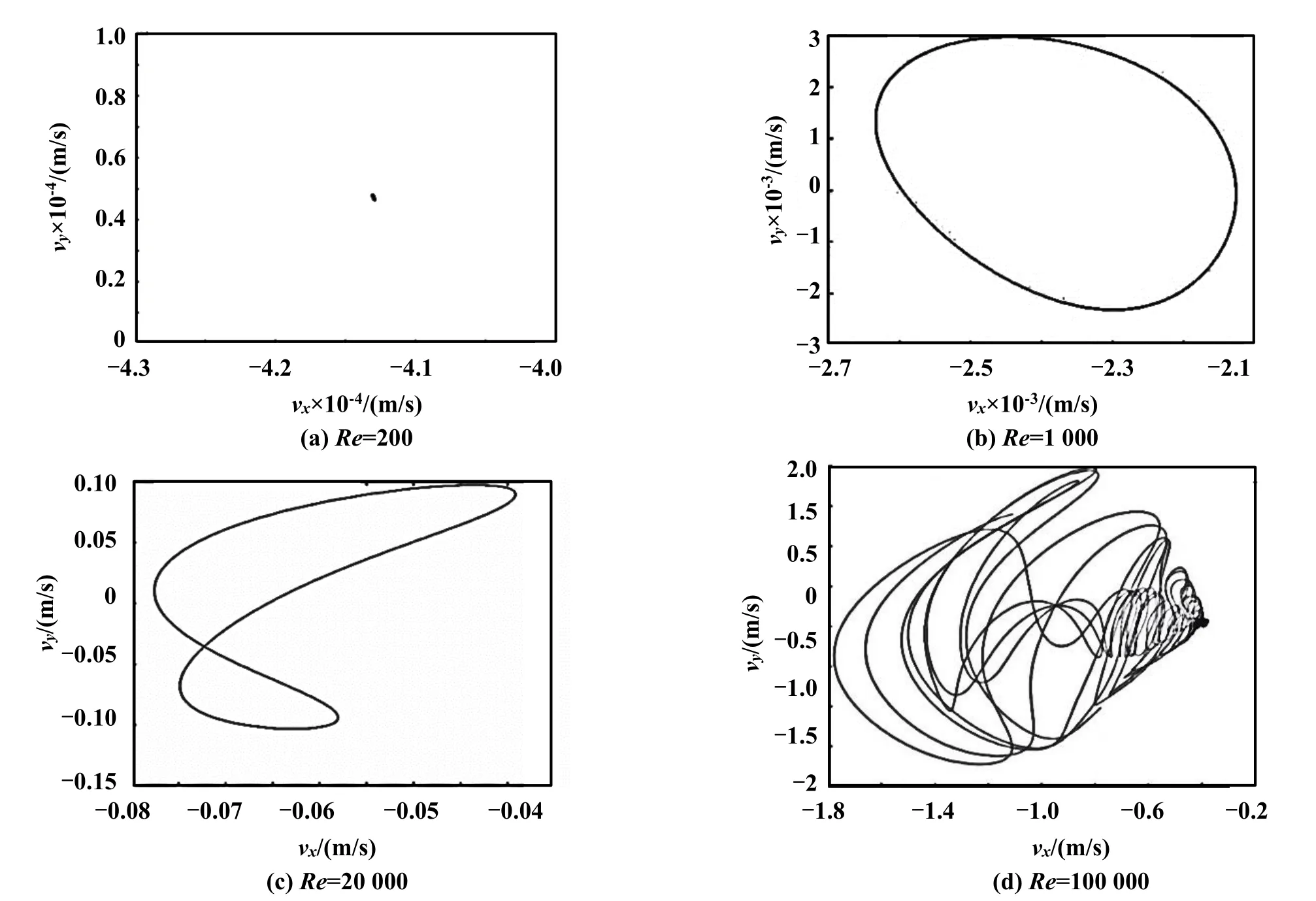
图3 不同Re下的监测点速度相图

图4和图5所示为Re分别为200和250时，监测点速度随时间的变化曲线及其速度场分布。由图4可知，当Re为200时，监测点的速度不随时间产生变化，此时的速度场对称分布；当Re为250时，监测点的速度出现周期性振荡现象，速度场出现了非对称现象；当Re继续增大时，速度场的分布不再对称，最后进入混沌状态。

图4 Re=200时的监测点速度及流场分布

图5 Re=250时的监测点速度及流场分布

4.1.2 不同Re的局部Nu

图6所示为不同Re下，管束中换热管局部Nu数的分布。可见，当Re＜250时，其速度场分布对称，传热系数在圆管周围也呈对称分布现象。当Re继续增大至250时，由于速度场分布不再对称，导致换热管的局部放热也不再对称，φ=0°～180°时换热管的局部换热要强于φ=180°～360°的表面，换热表现为非对称性，即换热非线性。

图6 不同Re下局部换热Nu分布

4.2 管束空间内的失稳现象

对6×9布置的换热器管束空间内的流动传热进行数值模拟时发现，末排管后的流场随着Re的变化，会出现突变，如图7所示，当Re=10时，计算域内的整个流场的分布完全对称。

图7 不同Re下的速度场

而当Re增大到100时，流场的分布会随流动时间出现突变，整个流场往下偏斜；若Re继续增大，流场变化出现振荡。对于该现象，本文认为这是由于流动出现了失稳而导致的，从非线性动力学的角度出发，在低Re下，流场的解对称；当Re增大时，流场便出现了静态分岔，速度场将会向一侧偏斜；若Re继续增大，流场便会出现动态分岔，速度场会出现振荡。

5 结论

本文对管束空间内的非线性现象进行了研究，当Re改变时，能够得到问题的对称解、非对称解；在实际工程应用时，即使换热器物理模型以及给的边界条件完全对称，但雷诺数Re一般较大，处在不对称解区，造成换热器局部换热强弱的问题，得出如下结论：

1）通过计算管束流场内监测点的速度相图可知，在低Re下，流场为稳定定态解，监测点速度不随时间的变化而变化；当Re增大时，速度相图逐渐从单个周期转变到倍周期，流场随时间呈周期性变化；若Re继续增大，流场便进入了混沌状态；

2）Re小于临界Rec时，为对称解；Re大于临界Rec时出现非对称解；在本文给定的几何和物理条件下，临界Rec约为250，当Re低于250时，流动和换热呈对称场分布；Re大于250时，流动和换热呈非对称偏斜状态，并且随着Re的增大，非对称现象越发明显；

3）在横掠管束的流动中，即便流场分布是对称的，也会出现失稳现象，流场会突然呈现偏斜状态；对于本文6×9布置的换热器而言，当Re大于100时，流场出现失稳现象，该现象与烟可视化实验中的流动非对称现象吻合良好。