基于双环相位结构的行人相位设置方法

梁子君，孔 微，李 军

( 1.合肥学院 城市建设与交通学院，合肥 230601；2. 安徽达尔智能控制系统股份有限公司，安徽 芜湖 241000)

随着城市交叉口交通精细化管理需求的日益凸显，行人过街的效率与安全性是一个不可忽视的问题。传统交叉口信号相位的设置往往以满足车辆通行需求为主，行人专用信号灯相位数量较少而且相位和过街时间设置还需改进和完善[1]。行人等待红灯时间过长或在一次过街时间内不能顺利过街，则容易导致行人强行穿越交叉口，不仅大大降低了交叉口的通行效率，同时也存在交通事故风险。为了改进行人过街的控制效果，不少学者对行人相位的设置以及信号控制开展了研究。行人二次过街信号相序多目标优化[2]、单进口放行方式下行人嵌套相位设计[3]、行人二次过街控制方案优化设计[4]、多相位信号控制交叉口行人相位设置方法[5]等主要通过设置交叉口中央安全岛和行人二次过街信号相位的方式，提高行人过街的效率，并以行人延误为优化指标进行了计算和验证。交叉口行人专用相位设置阈值[6]以延误成本和冲突成本分别作为效率与安全的评价指标，提出了行人专用相位的设置条件。基于行人专用相位的信号控制优化模型[7]、行人专用相位动态设置方法[8]、考虑人车交互的交叉口行人专用相位设置[9]在两相位信号控制交叉口的基础上，提出了行人专用相位的设置模型和方法。行人过街信号清空时间设置[10]、基于感应控制的行人二次过街系统设计[11]和行人安全过街智能系统[12]对行人过街信号配时开展了研究并实施了智能控制，Ma等[13]和Zhang等[14]提出了专用行人相位的设置模式、信号配时与安全分析。上述研究成果均为本文提供了重要的方法和理论基础，然而关于行人相位的通用设置方法和切换结构方面尚未提及，一种灵活的在线信号相位切换结构[15]在美国NEMA TS2标准中的双环相位结构基础上提出了机动车和行人相位切换结构，为本研究提供了重要思路，但行人相位设置考虑较为简单，没有考虑行人二次过街的信号相位设计，尚未形成通用方法，且缺乏案例的效益指标分析。

为此，主要在双环相位结构原理的基础上，考虑通用情况下的行人二次过街相位设计，研究与机动车流向不冲突的行人相位组合设计方法，并提出增加行人相位的双环相位切换结构。通过实际交叉口的调查数据进行交通仿真，验证方法的有效性，对于交叉口机动车与行人相位的灵活设置以及控制效率的有效提升具有现实意义。

1 双环相位结构原理

1.1 机动车流向分布

美国电气制造商协会NEMA(National Electrical Manufacturers Association)定义了交通信号相位标准，对十字交叉口8个主要受信号控制的机动车流向进行了说明，如图1所示。

图1 交叉口受信号控制的机动车流向分布

这些流向是各个进口的直行和左转流向，其中，左转车流编号为奇数，从南进口开始顺时针标记，直行车流编号为偶数，从北进口开始顺时针标记。右转车流在避让通行的前提下可不受信号控制，非机动车与行人流向默认跟随不冲突的机动车流向通行。

1.2 双环相位结构

将图1的8个机动车流向按顺序放入双环控制结构中，形成双环相位结构如图2所示。

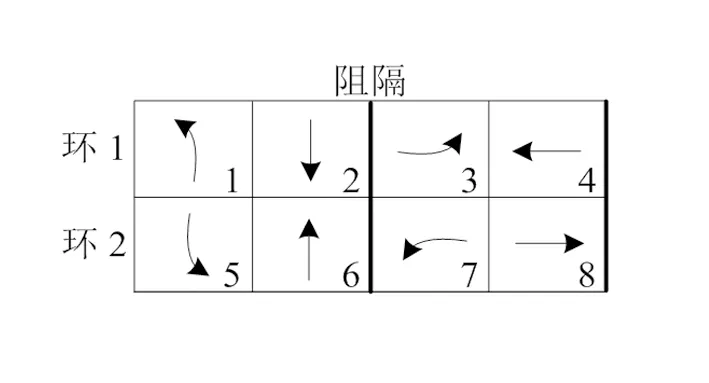
图2 双环相位结构

双环相位结构的基本控制逻辑为：同一环中的车流不可组成一个相位，不在同一环中但在阻隔同一侧的任意两个车流可以组成一个相位，阻隔同一侧的车流需要放行结束后，才能放行阻隔另一侧的车流。该控制逻辑保证了在阻隔同一侧的环1和环2之间的车流没有冲突，可以各自独立地进行控制，则根据每股车流通行需求的不同，每股车流的放行时间可以不同，如图3所示，环1中车流1的放行时间大于车流2，车流3的放行时间小于车流4，环2中车流5的放行时间小于车流6，车流7的放行时间大于车流8。

图3 车流通行需求不同的双环相位结构

图2的双环相位结构形成的相位组合如图4所示，在环1和环2对向左转和对向直行车流通行需求相同的前提下，形成常规对称放行的四相位。图3的双环相位结构形成的相位组合如图5所示，对向左转和对向直行车流通行需求不相同的前提下，相比图4增加了两个搭接相位，分别是车流1和车流6搭接形成的搭接相位2，以及车流3和车流7搭接形成的搭接相位5。

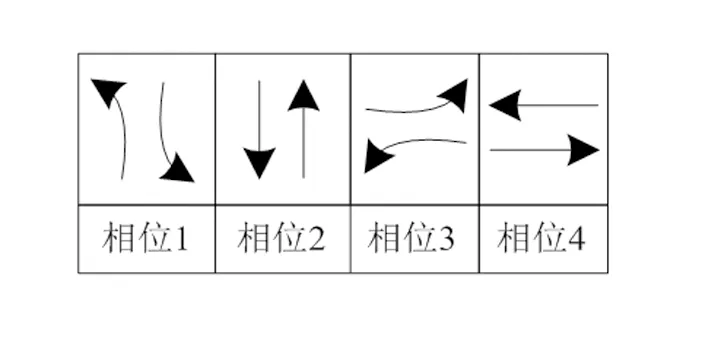
图4 常规对称放行的四相位

图5 具有搭接相位的相位组合

双环相位结构中，根据环1和环2车流通行需求的不同情况，还可以形成更多不同的相位组合，最终可形成通用的双环相位切换结构如图6所示。

图6 双环相位切换结构

2 双环相位结构的行人相位设计

2.1 行人流向分析

为考虑交叉口行人相位设计的通用情况，假设十字交叉口四个方向均具备中央安全岛，行人可采用二次过街的方式通过交叉口，则行人流向在交叉口中可以划分为8个不同的流向，在图1已有车流编号的基础上，以编号9开始从南进口开始顺时针标记至编号16，如图7所示。

图7 交叉口行人流向分布

由于信号相位设计中，行人相位一般跟随不冲突的机动车相位放行，在双环相位结构中，不同的机动车相位组合是由机动车流向组成的，因此有必要分析与单个机动车流向不冲突的所有行人流向，在此基础上再分析不冲突的机动车流向组合所形成的机动车相位以及可跟随放行的行人相位。根据图7的流向分布，以单个机动车流向为依据，可以形成非冲突行人流向集合Qi见表1所列。

表1 单个机动车流向对应的非冲突行人流向集合

2.2 行人相位组合设计

根据双环相位结构的控制逻辑，设在阻隔同一侧的环1中任一车流i和环2中任一车流j可组成一个相位组合Pij，跟随Pij放行的行人相位组合为Pij，表1中车流i对应的非冲突行人流向集合为Qi，车流j对应的非冲突行人流向集合为Qj，由于Pij所包含的行人流向应均与车流i和车流j不冲突，则Pij包含的所有行人流向即为车流i和车流j所对应的非冲突行人流向集合Qj与Qi的交集，记为Qi∩Qj。根据图6中不同的机动车相位组合，对应可跟随放行的行人相位组合见表2所列，增加行人相位的双环相位切换结构如图8所示。

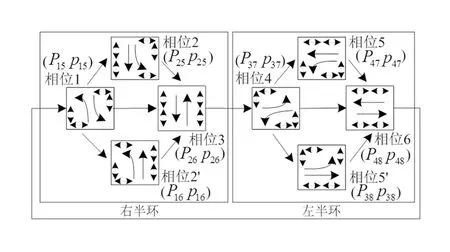
图8 增加行人相位的双环相位切换结构

表2 双环相位结构中的行人相位组合

特别是双环相位结构中阻隔同一侧的车流按照实际通行需求不能同步放行结束时，说明交叉口车辆流量分布存在较大差异，此时若阻隔同一侧的车流继续同步放行结束，必然会导致其中一个流向的绿灯损失，如图9所示，环1中的流向4早于环2中的流向8结束，环2中流向6早于流向2结束，流向4和流向6的阴影部分表示这两个流向的绿灯损失。

图9 双环控制结构中阻隔同一侧的车流不同步放行结束

为避免上述的绿灯损失，此时环1或环2中已放行结束的机动车流向不再开放绿灯，尚未放行结束的机动车流向所对应的非冲突行人流向可提前放行，即在满足交叉口车辆实际通行需求的前提下，行人可以获得更多的过街时间，此时进一步增加的行人相位组合见表3所列，对应的双环相位切换结构如图10所示。

表3 双环相位结构中进一步增加的行人相位组合

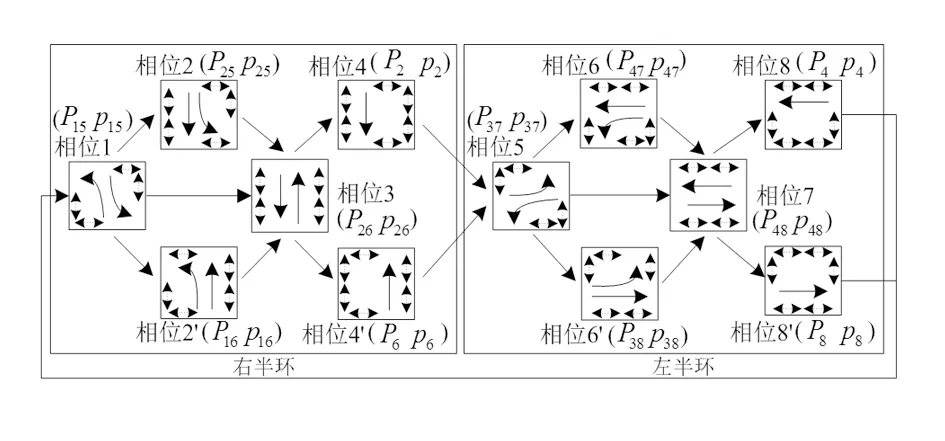
图10 进一步增加行人相位的双环相位切换结构

2.3 行人相位信号配时

由于行人过街具有聚集性特征，为保障行人安全过街的同时降低对车辆通行效率的影响，行人应能够在一次较短的行人绿灯时间内进入交叉口，并在一段足够长的清空时间内保证最后进入交叉口的行人能够按一定的步速从一个安全的驻足区到达另一个安全的驻足区。因此，行人过街时间应由行人绿灯时间和行人清空时间组成，计算式见式(1)。机动车相位最小绿灯时间应能满足行人过街时间的需求，行人过街时间是机动车相位绿灯时间的重要约束条件之一，计算式见式(2)。

(1)

其中，td为行人一次过街时间(s)，t1为行人绿灯时间(s)，t2行人清空时间(s)，t2时间段内行人不得进入交叉口，但已进入交叉口的行人可继续安全过街。L0为行人一次过街距离(m)，v0为行人过街平均速度(m/s)。

(2)

其中，gmin为机动车相位最小绿灯时间(s)，I为绿灯间隔时间(s)，其余同上。

从式(1)(2)可以看出，7 s是行人最小绿灯时间的经验值，行人在机动车相位的绿灯间隔时间内仍可以过街，由于行人相位跟随机动车相位放行，因此行人相位绿灯时间最终由机动车相位绿灯时间计算得出，见式(3)。

(3)

其中，g为机动车相位绿灯时间(s)，其余同上，绿灯间隔时间I的计算见式(4)。

(4)

其中，Y为黄灯时间(s)，r为全红时间(s)，tu为通过时间(s)，SC为基本清空距离(m)，vc为车辆清空速度(m/s)，Lv为车辆长度(m)，Se为进入距离(m)，ve为进入交叉口速度(m/s)。

图10中行人流向连续在多个机动车相位放行时，其获得的行人绿灯时间应是多个机动车相位时间之和再减去该行人流向所需的清空时间。

3 交通仿真分析

3.1 交叉口基础条件

选取合肥市锦绣大道与蓬莱路交叉口工作日15∶30至17∶30时段的交通数据进行仿真建模和分析。交叉口平均每小时机动车和行人流量数据调查见表4所列，其中东、西进口的机动车流量存在较大差异。交叉口渠化和流向编号分布如图11所示，锦绣大道是东西走向的主干道，蓬莱路是南北走向的次干道，交叉口四个方向均具备行人过街中央安全岛，交叉口Vissim交通仿真模型如图12所示。

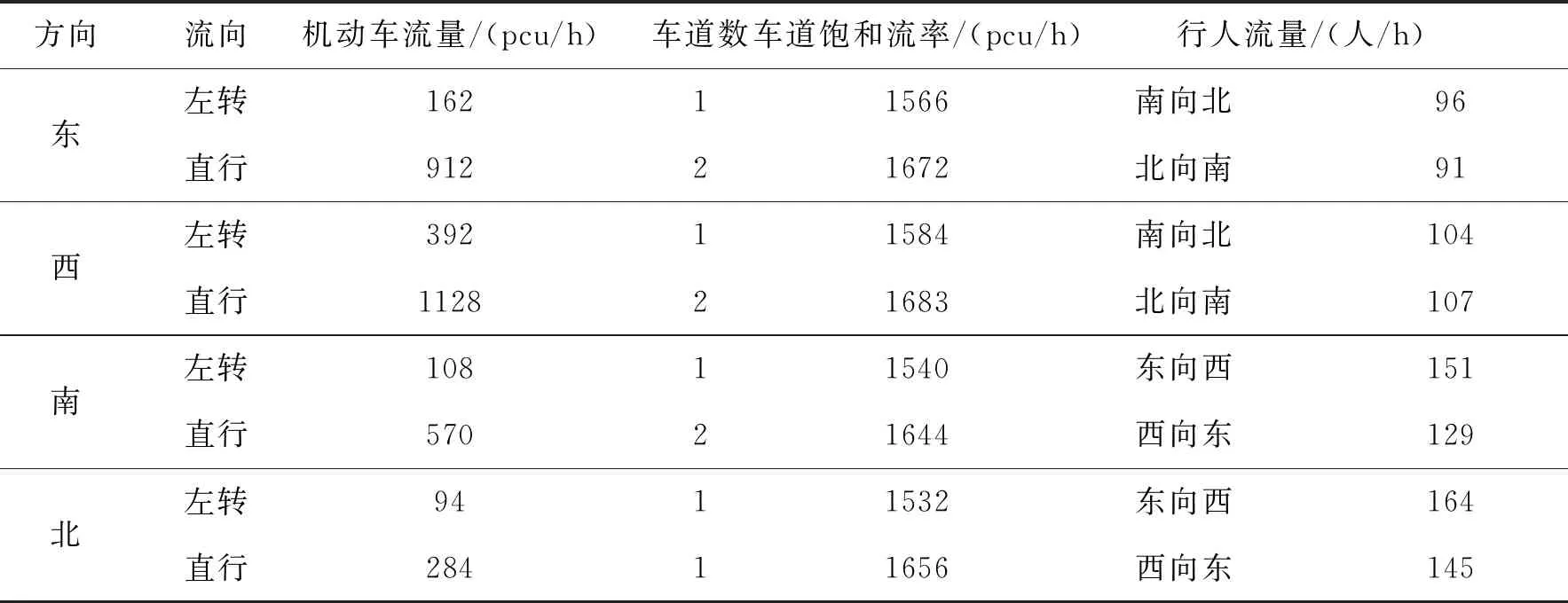
表4 交叉口15∶30至17∶30时段平均每小时流量数据

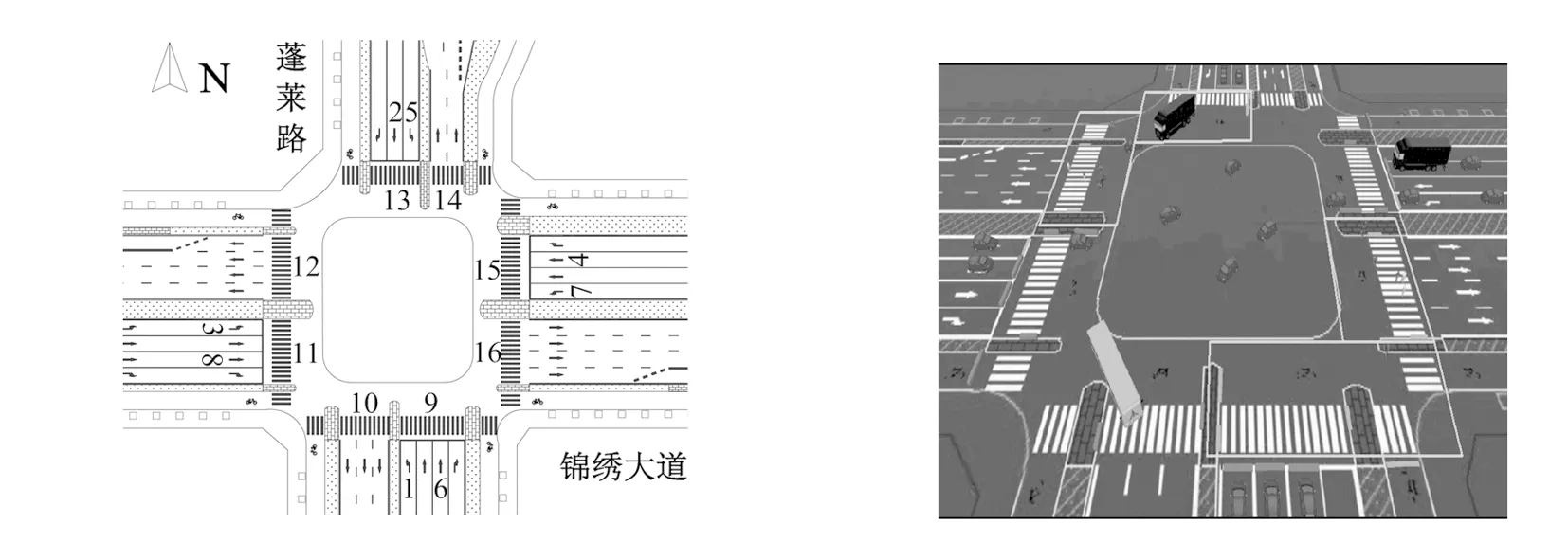
图11 交叉口交通渠化和流向编号分布 图12交叉口交通仿真模型

3.2 信号控制方案设计

根据表4交通数据和图11交叉口渠化，依据图10分别采用常规对称四相位、搭接相位和进一步增加行人相位的搭接相位开展方案设计，形成相位方案A、B和C，如图13所示。行人过街均采用二次过街的方式，在各相位中只要与机动车流向不冲突均可放行。针对各相位方案，采用韦伯斯特法进行信号配时设计，其中机动车信号配时见表5，行人信号配时见表6。

a. 相位方案A b. 相位方案B c. 相位方案C

表5 机动车信号配时 单位：s

表6 行人信号配时 单位：s

3.3 仿真结果分析

将相位方案A、B、C以及各自对应的机动车与行人信号配时方案导入图12的交叉口仿真模型中，以表2流量数据运行仿真3600 s，对比分析相位方案A、B和C的交通效益。其中交叉口车辆延误仿真运行结果部分截图如图14所示，不同方案车辆延误统计结果见表7所列，对应的分析结果见表8和图15所示；行人过街行程时间(含红灯等待时间)仿真运行结果部分截图如图16所示，不同方案行人过街行程时间统计结果见表9所列，对应的分析结果见表10和图17所示。

图14 车辆延误仿真运行结果(方案B)

表7 不同方案车辆延误统计结果 单位：s

表8 不同方案车辆平均延误分析结果 单位：s

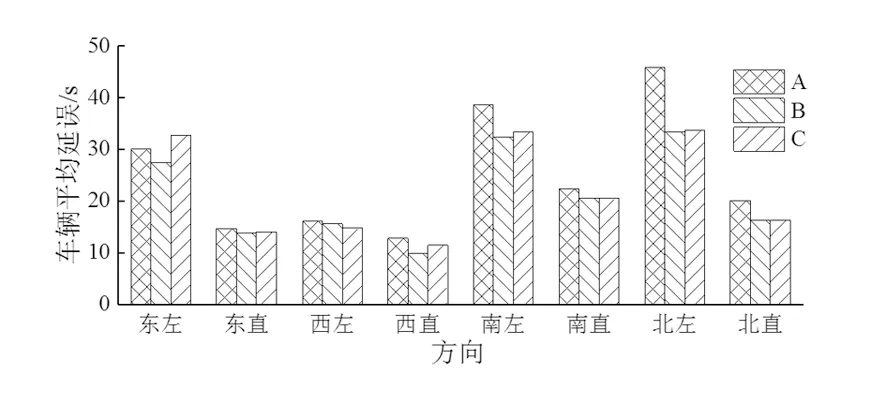
图15 车辆平均延误分析结果

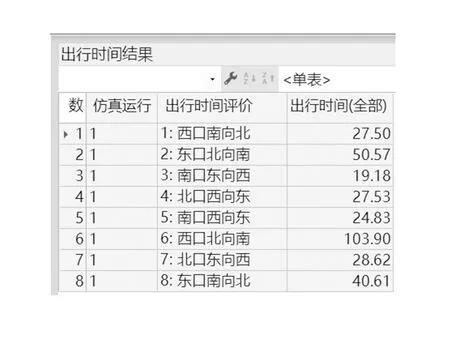
图16 行人过街行程时间仿真运行结果(方案B)

表9 不同方案行人过街行程时间统计结果 单位：s

表10 不同方案行人过街平均行程时间分析结果 单位：s

图17 行人过街平均行程时间分析结果

图15中相位方案B和C的车辆平均延误均比方案A有所降低，平均降低了15.6%和11.9%，原因是东、西进口的单车道平均流量存在较大差异，方案B和C在东西方向采用搭接相位设计，使车道流率比更为均衡，计算所得信号周期比方案A降低了28.9%。而相位方案C的车辆平均延误比方案B平均增加了4.2%，原因是交叉口西直行的交通需求放行结束后东直行仍然存在交通需求，方案C把同一个半环中的东左转和西直行多出的绿灯时间分给不冲突的行人相位，因此在东左转和西直行方向的车辆平均延误比方案B有所增加。

图17中相位方案B和C的行人过街平均行程时间(包括红灯等待时间)均比方案A有较大降低，平均降低了18.1%和23%，原因是相位方案B和C的信号周期时间比方案A有明显降低。而方案C的行人过街平均行程时间比方案B平均减少了5.9%，原因如上所述，方案C把机动车多余的绿灯时间分给不冲突的行人相位，行人获得了额外的绿灯时间。

4 结语

针对交叉口行人相位尚未形成通用设置方法和切换结构的情况，在灵活的双环相位结构基础上，考虑行人二次过街通用需求，进一步提出了与机动车流向不冲突的行人相位组合设计方法。通过分析双环相位结构中与各个机动车流向不冲突的所有行人流向集合，创新地形成了适应交叉口车流量分布不均的增加行人相位的双环相位切换结构，特别是当双环相位结构中阻隔同一侧的车流通行按照实际需求不同步结束时，非冲突行人流向可提前放行，在满足交叉口车辆实际通行需求的前提下，可保障行人获得更多的过街时间，为灵活设置交叉口机动车与行人相位并进一步提升控制效率提供了有效借鉴。

通过实际交叉口的交通仿真验证表明，本文方法在双环相位结构基础上能够灵活的设置行人相位，特别是在交叉口流量分布不均的情况下，双环相位结构更适宜采用进一步增加行人相位的搭接相位方案，相比常规的对称相位方案，交叉口车辆平均延误和行人过街平均行程时间均有明显降低。

在交叉口流量分布相对均匀的情况下，采用常规对称相位的控制效率可能会更好。提出的增加行人相位的双环相位切换结构所对应的不同相位方案设置取决于交叉口不同的流量分布条件，可以在交通仿真软件中设置不同的流量等级统筹分析不同机动车和行人相位方案的适用性条件，也是后续需进一步开展的研究工作。