非人工干预条件下粮堆温度场的研究

王振清，张祥祥，陈 曦

(河南工业大学 土木工程学院，郑州 450001)

我国储备粮库多采用的平房仓、浅圆仓、立筒仓等仓型均为地上仓，地上仓外界温度为大气温度，气温随季节更替而变化。而地下仓依托其天然低温环境能抑制粮内酶活性、减弱粮粒呼吸作用和免去药物熏蒸，实现绿色储粮也越来越得到重视[1-2]。温度作为安全储粮的主要物理因素之一，研究价值巨大。仓内温差亦会产生微气流，在粮堆内部形成自然对流，从而导致仓内水分分布不均[3]。因此，为了保证安全绿色储粮，研究并改善粮仓内温度场具有重要意义。

数值模拟经济有效，在对于探索粮堆温度场传递规律中被广泛应用[4]。国内外学者对不同仓型内粮堆温度场和微气流场进行了大量的研究。梁醒培等[5]采用有限元法对小麦粮堆进行了一年的温度模拟，并用实仓验证了模拟的准确性；Jia等[6]在笛卡尔坐标系下构建了圆筒仓粮堆温度场模型；Thorpe[7]通过对多孔介质中的热量传递进行研究，运用计算流体力学(CFD)模拟软件构件了粮堆的热湿传递模拟；尉尧方等[3]基于多孔介质传热传质理论，采用近似分析原理和数值模拟方法，对储粮期间粮堆内的自然对流过程和温度场传递规律进行了探究，得出自然对流使得粮堆温度更加均匀；刘文磊等[8]基于数值模拟软件COMSOL，探究了储粮压力对粮堆温度场的影响，并得出储粮压力影响下的粮堆内温度场变化规律，并用试验验证了其可靠性；葛蒙蒙等[9]利用数值模拟软件COMSOL，对高大平方仓静态储藏温度场变化进行了研究，得出仓内粮堆温度变化受外界温度影响较大，表现出季节性变化，并用试验验证了模拟的准确性；王振清等[10-12]对地下仓储粮期间温度场变化进行了数值模拟分析，得出随着储粮时间的增加，仓内粮堆温度逐渐趋于当地地下恒温温度。粮温温度的分布在纵向存在明显分层现象且外界温度对粮堆上层的影响要高于下部，并用试验验证了模拟的准确性。

国内外学者对粮堆温度场的研究多集中于地上仓，对地下仓温度场的研究有所涉及，但仍相对较少。采用地上与地下仓对比的方法，对粮堆温度场进行了为期1年的数值模拟，分析了粮堆温度和微气流的动态变化规律，进而为制定相关措施提供依据。

1 粮仓模型的建立与条件设置

粮堆是一种多孔介质，其储藏期间，涉及温度的传递和微气流流动等。为简化计算，假定粮堆为多孔介质域，且均匀连续分布，忽略粮堆自呼吸影响及粮粒间辐射作用。

1.1 非人工干预条件下数学模型的建立

假定空气为不可压缩流体，连续性方程为：∂u/∂x+∂v/∂y=0

(1)

自然对流中，Ra=Pr*Gr= v/α·(gβL3△T)/V3

(2)

其中：Gr为格拉晓夫数；Pr为普朗特数；g为重力加速度，m·s-2；β为流体体积膨胀系数，1/K；T为热力学温度，K；L为特征长度，m；v为运动粘度，m2/s；α为热扩散系数，m2/s；△T为流体上下面温差值。

假定自然对流速度场足够小(Ra<1)，达西定律能够适用，则X、Y方向速度分别是：

u=K/μP

(3)

v=-K/μ(P-ρag)

(4)

则质量守恒的方程可写为：(∂(ερa))/∂t+(ρauj)=0

(5)

式中，μ为动力粘度系数，N·s/m2；K为渗透率，m2；ε为孔隙率，ρa为空气密度，kg/m3；uj(j=1,2)为xj方向空气的流动速度，m·s-1；u1=u，u2=v。xj(j=1,2)为系统坐标，在笛卡尔坐标系中，x1=x，x2=y，x，y即为笛卡尔坐标系中x轴，y轴。

假定浮升力满足线性变化，采用Boussinesq近似[13]，则动量方程为：

ρa(∂ui)/∂t=-(φμui)/K-∂P/xi+δijρag(T-T0)

(6)

能量守恒方程：

ρgCg∂T/∂t+·(-kgT)=Q-ρaCauj·T+τ:S+T/ρa((∂ρa)/∂T)P(∂P/∂t+uj·P)

(7)

忽略压力功、粘性发热和由于粮食颗粒自呼吸产生的热量，则能量守恒方程简化为：

ρgCg∂T/∂t+·(-kgT)+ρaCauj·T=0

(8)

式中，ρg为粮食密度，kg/m3；Cg为粮食比热容，J/(kg·K)；kg为粮食导热系数，W/(m·K)。

1.2 物理模型的建立与域点探针布置

1.2.1物理模型仓视图

仓高5 m，外直径3.5 m，中心筒直径0.5 m，其中装粮线高4 m，装粮线上至仓顶盖区域为空气域，仓顶盖为绝热材料，地下均温为17℃。在仓内布置探针用于记录温度变化，域点探针从下至上共布置5层，每层4个，共布置20个。域点探针对称布置在仓中心面，水平间距为500 mm，垂直间距为1000 mm，空气域内域点探针与装粮线间距为500 mm。仓俯视、剖面图和域点探针布置图见图1和图2。

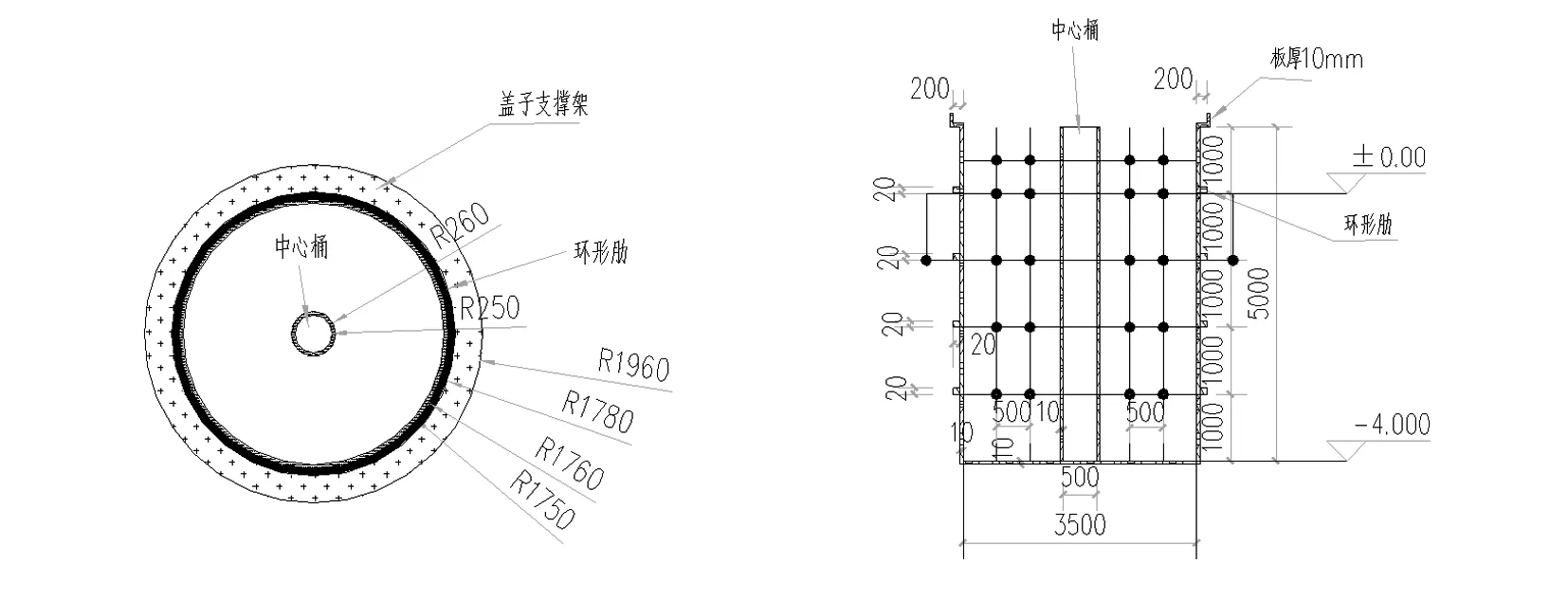
图1 模型仓俯视示意图 图2 模型仓剖面及探针布置图

1.2.2COMSOL边界条件及参数设置

对模型仓进行为期1年的模拟，模拟装粮时间为10月份。环境温度为金立兵等[12]实测数据，测试地点为河南郑州。

数值模拟初始条件：初始粮温为20℃，地上仓初始环境温度采用差值函数的形式，用实测的每月温度的平均值为边界温度条件；地下仓外部环境温度取地下均温17℃，仓内空气域温度为初始环境温度20℃；数值模拟边界条件如表1：

表1 数值模拟边界条件

2 结果分析

利用建立的粮仓COMSOL二维物理模型，在非人工干预条件下，对地上仓和地下仓两种不同粮仓形式内温度场和微气流场进行数值模拟。模拟时长为期1年，数值模拟主要研究了非人工干预条件下粮仓内的温度传递过程，通过数值模拟给出粮堆的微气流场(速度场)、温度场，以及多孔介质域温度变化过程。

2.1 速度场对比分析

对比分析两种储粮方式速度场云图(图3～图6)可知，其分布趋势相同。粮堆空隙间的速度场主要是由于温差导致的密度不均而形成，靠近高温壁面粮堆的中部处微气流较强。中间部位由于中心筒的存在使得靠近中心筒壁处微气流略微增大，中心筒壁与仓壁之间存在一条微气流低速带。在地上仓中，外部环境温度升高使得微气流区域沿壁面略微升高；地下仓中随着冷量渗入粮堆，由温差产生的微气流逐渐减小。在1月份和7月份，地上储粮方式的边界温度与粮食温差大于地下储粮方式边界温度与粮食温度的温差(3℃)，故地上仓速度场分布值大于地下储粮方式，但由于温差相差不大(10℃以内)，所以速度场数量级均在10-5～10-4m·s-1，且均呈现“)(”状态，地上仓1月份微气流最大值为(9.52×10-4m·s-1)>地下仓1月份微气流最大值(1.67×10-4m·s-1)，7月份亦是相同趋势，微气流的大小导致温湿度在地上仓内扩散速度大于地下内扩散速度。

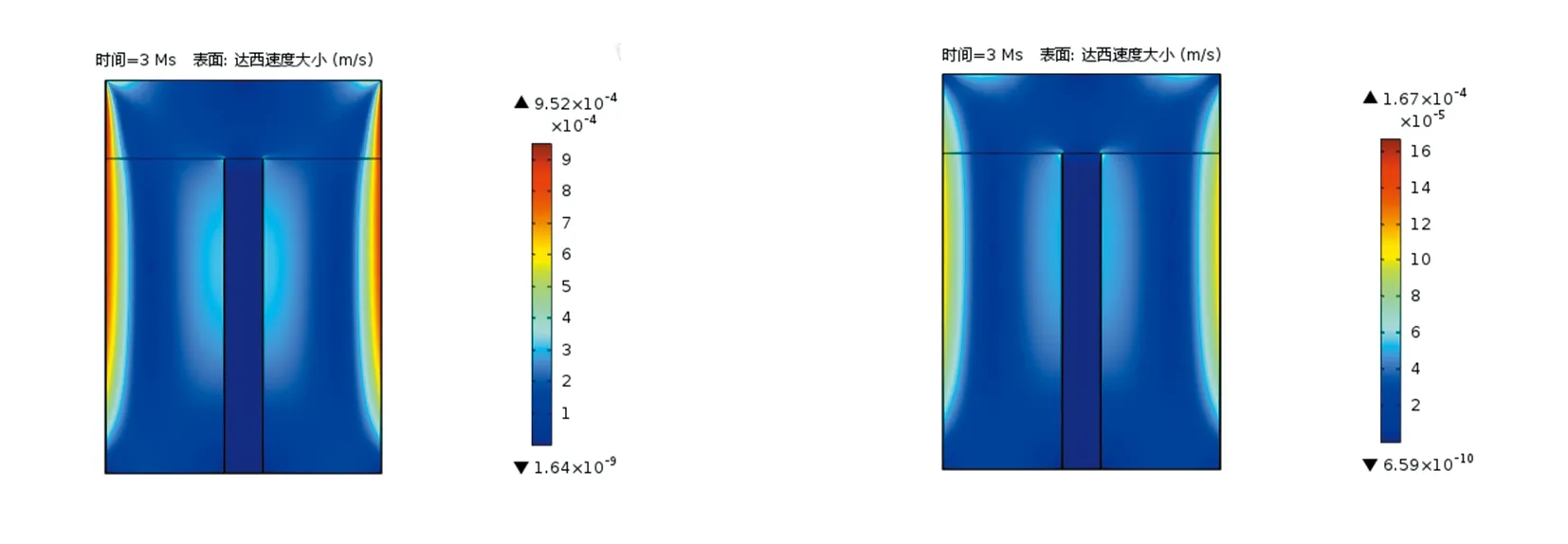
图3 地上仓1月份速度场 图4 地下仓1月份速度场

图5 地上仓7月份速度场图 图6 地下仓7月份速度场

2.2 温度场对比分析

对比分析两种储粮方式温度场云图(图7～图10)可知，粮堆温度场关于中心筒呈现对称分布。随着时间的推移，在地上仓的粮堆中，首先是冷量不断向粮堆中扩散，使得粮堆中高温区域逐渐减小，低温区域逐渐增加；高温区域由于热浮升力的作用，表现出热区域上浮的现象。储粮3个月，多孔介质域最大值为18.6℃，比初始温度降低1.4℃。随着天气变暖，外界温度升高，粮堆的温度出现滞后现象，且冷量积聚在粮堆内部，表现出冷量下沉的现象；由于地下仓边界温度较稳定，在地下仓的粮堆中，冷量不断向粮堆中扩散，使得低温区域不断增大，高温区域不断减少。储粮九个月，粮堆的最大值为18.4℃，比初始粮温降低1.6℃。由于温度差产生微气流，微气流又影响温度的分布，使得粮堆中高温区域上升，低温区域下降。同时，由地上、地下仓对比可直观看出，当外部高温时粮仓内形成“热皮冷芯”；当外部低温时粮仓内形成“冷皮热芯”，两种现象的出现对安全储粮带来隐患。

图7 地上仓1月温度场 图8 地下仓1月温度场

图9 地上仓7月温度场 图10 地下仓7月温度场

2.3 各层粮温对比分析

根据在COMSOL中定义的域点探针和域探针，对粮堆各层、空气层(第五层)和整体温度平均值的变化进行分析。由图11可知，在地上仓中，外部环境温度的变化使得仓内粮堆温度发生相同趋势的变化，且外部环境对粮堆温度的影响随着层高的增加逐渐减小。装粮5个月后，粮堆上下层温差最大，达3.7℃。空气层受外界环境温度影响最大，在初始温差较大时出现骤降的现象；由图12可知，在地下仓中，由于外界环境温度较稳定，仓内粮堆温度随着储粮时间的增加逐渐降低，距离仓底越近处粮堆温度受外界温度影响最大。装粮一年后，第一层粮堆温度均值降低2℃，第三层温度变化最为缓慢，装粮一年后，均温降低1.5℃。由图13可知，地上仓粮堆温度受环境温度影响较大，其粮堆温度均值波动较大，而地下仓仓内粮堆温度均值平稳变化。在外部环境温度变化时，地上仓仓内粮堆温度均值表现出与外界环境相同的变化趋势，但却有“滞后”现象，这是由于粮食作为一种热导体，具有热阻，使得温度在粮堆内的传递需要一个过程。

图11 地上仓各层温度变化图 图12 地下仓各层温度变化图 图13 粮堆均温随环境温度变化图

2.4 结论与建议

本文基于数值模拟软件COMSOL对郑州一地上粮仓和一地下粮仓进行了装粮周期为1年的数值模拟，通过实测的环境温度为边界条件，模拟了仓内温度场和微气流场变化，主要得出以下结论与建议：

(1)非人工干预条件下，微气流数值较小，其均值数量级均在10-5～10-4m·s-1，且均呈现“)(”状态，靠近粮堆中心位置速度最大；

(2)地上仓中环境温度变化直接影响仓内粮堆温度变化，且波动较大，在装粮后约5个月后与初始粮堆温度差达到最大，为10.5℃。地下仓由于外界环境温度较稳定，仓内粮堆温度变化平稳，7月末仓内粮堆最高温度为18.4℃，降低1.6℃，能给予粮堆较低的储粮温度，这对于给予粮堆恒定的储粮温度优势明显；

(3)外部环境对地上仓和地下仓仓内粮堆温度的影响，都会随着层高的增加而降低。仓内粮堆温度的变化在随着外部环境温度变化的同时，表现出“滞后”的现象。在地上仓中，装粮5个月后，粮堆上下层温度差达到最大值3.7℃；地下仓中，装粮一年后温度降低2.6℃，且中间层粮堆受外部环境温度变化的影响较小。

(4)实际储粮过程，可通过改变装粮时间来改变装粮温度，从而改善仓内温度场，使仓内温度更有利于安全储粮。