电子节气门T-S模糊控制方法研究

李学军，于皓宇，李 昊

(长春大学 电子信息工程学院，长春 130022)

随着汽车行业的飞速发展，国家新排放标准的出台。人们对汽车的动力性、安全性，驾驶的舒适性以及较低的油耗和尾气排放等有着更高的要求。研究电子节气门的控制方法对提高以上指标有着现实意义。国内外学者作了大量研究。文献[1]设计了变结构滑膜控制器，设定一个滑膜面，当状态空间中的点穿过滑膜面时，改变其输出控制量的结构，试验证明该方法提高了电子节气门控制系统的响应速度。但当状态轨迹运动到滑膜面附近时，不能精准地沿着滑膜面运动，而是在滑膜面附近反复穿越，因此会给系统带来抖振。文献[2]基于Mamdani模型设计模糊控制器，该方法的后件输出为模糊集合，电子节气门控制系统只能接受一个精确的控制量，需对输出模糊集合进行去模糊处理结构复杂且不利于计算和数学分析。文献[3]采用backstepping方法设计了电子节气门系统控制器，该方法要求系统各状态量可测，但在实际系统中阀片的角速度难以测得，一般采用阀片位置信息的微分信号来代替。这样做可能会放大采样噪声，影响控制精度。文献[4]提出了基于神经网络的模型参考自适应控制算法，使用神经网络系统辨识器模型配置基于MRAC的电子节气门神经网络控制器，实现对电子节气门控制系统的高精度控制。但是由于神经网络在线估计运算量大，用于实际系统时对处理器的性能要求较高。

设计了一种基于T-S模型的模糊控制器，整个控制器的设计基于模糊控制理论和现代控制理论。以节气门开度偏差和偏差变化率作为模糊控制器的输入变量，将整个非线性系统根据不同的模糊规则划分为多个子系统，每条规则的输出控制律以线性多项式的形式表达。最后利用重心法计算得到T-S型模糊控制器的最终控制律。通过仿真试验，验证该方法的可靠性和鲁棒性。

1 电子节气门数学建模

电子节气门主要由阀体、驱动电机、减速齿轮组、回位弹簧、阀片、位置传感器组成。其中影响电子节气门非线性特性的主要原因是复位弹簧的弹簧扭矩变化。

由基尔霍夫定律知直流电机回路方程和扭矩方程：

(1)

U(t)=Uc·u(t)，

(2)

Tm(t)=kt·i(t)，

(3)

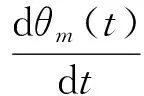
忽略等效电感，整理式(1)～(3)得：

(4)

受主轴惯性力矩和自身摩擦力矩的影响，实际输出扭矩的关系式如下：

(5)

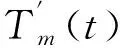
摩擦力矩，可简化为库伦摩擦力矩和粘滞摩擦力矩两部分：

Tfri(t)=-kdω(t)-kfsgn(ω(t))，

(6)

其中，Tfri(t)是电子节气门阀片摩擦力矩，kd是粘滞摩擦力系数，kf是库伦摩擦力系数。

电子节气门阀片主轴惯性力矩为：

Tg(t)=Jg·a(t)，

(7)

其中，Tg(t)是电子节气门阀片主轴惯性力矩，Jg是电子节气门阀片主轴转动惯量。

复位弹簧的扭矩变化如图1所示。可以看出在整个工作区间呈非线性变化。

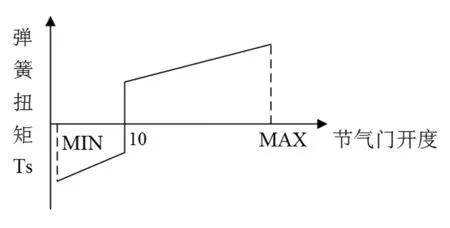
图1 复位弹簧的扭矩变化情况

复位弹簧的扭矩数学表达式为：

Ts(t)=kpresgn(θ-θ0)+ks(θ-θ0)，

(8)

(9)

其中，Ts(t)是复位弹簧扭矩，kpre是弹簧的预紧力矩系数，θ0是坡行回家开度一般在9°～15°之间，ks1是θ≥θ0时弹簧的弹性系数，ks2是θ0>θ≥0时弹簧的弹性系数。

根据扭矩守恒原理，方程表示为：

Tre(t)=Ts(t)+Tfri(t)+Tg(t)，

(10)

电子节气门的直流电机主轴和阀片主轴之间是靠减速齿轮连接起来的，设减速齿轮组的传动比为N，得到关系式如下：

(11)

把式(1)～(10)带入式(11)整理得到电子节气门的微分方程如下：

(12)

y=x1，

(13)

其中，a,b,c,d,e分别表示为：

2 T-S型模糊控制器设计

2.1 T-S模型

模糊控制从模型上划分可分为Mamdani模型和Takagi-Sugeno模型，T-S模型是Takagi和Sugeno于1985年提出的[10]，它是解决复杂非线性系统的一种典型的模糊模型。在T-S模型的模糊系统中，采用如下模糊规则：

(14)

式中，Ai(i=1,2,…,n)是输入量的模糊语言值，ci(i=1,2,…,n)是分布补偿增益。T-S模型的主要特点为：其规则前件采用模糊量的形式，后件输出是由各模糊规则的线性输出构成的多项式线性方程，使非线性系统的全局输出具有良好的线性描述特性。适用于解决电子节气门由复位弹簧和摩擦引起的非线性问题。

2.2 T-S型模糊控制器的结构及原理

根据模糊控制器输入维数的不同可分为3种结构形式。分别为一维、二维、三维模糊控制器。一维模糊控制器精度差，三维模糊控制结构复杂，故采用二维模糊控制器。针对电子节气门控制系统，选取节气门开度偏差e，开度偏差的变化率ce作为模糊控制器的输入变量。得到了二维输入的T-S型模糊控制器。其结构图如图2所示。

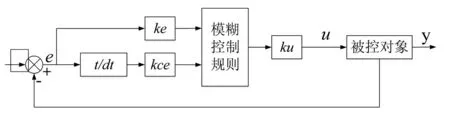
图2 T-S型模糊控制器原理图

其中，ke、kce分别为偏差e与偏差的变化率ce的模糊量化因子，ku为模糊控制器的输出比例因子。模糊量化因子是将输入变量从基本论域转换到模糊论域。其计算公式为n=kx·Δq，式中，kx是量化因子，n是模糊论域等级，Δq是被量化量的变化范围。因为电子节气门阀片实际工作角度为[0,90]度，从0度运动到90度约为90 ms。因此，定义e的变化范围为[-1.57,1.57],ce的变化范围为[-17.4,17.4]。计算得到ke,kce分别为3.821,0.172。为了得到最佳的控制参数，定义ku为模糊控制器输出参数比例因子，ku取值为10。

根据式(14)，可得到第k条模糊规则如下：

(15)

(16)

(17)

(18)

将式(17)(18)带入式(16)得：

(19)

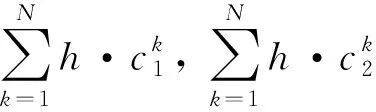
2.3 T-S模型模糊子集及隶属度函数

模糊子集的隶属度函数选取全对称、全交叠的三角和梯形隶属度函数。在节气门开度偏差e的模糊论域上定义5个模糊子集，在偏差的变化率ce的模糊论域上定义3个模糊子集。

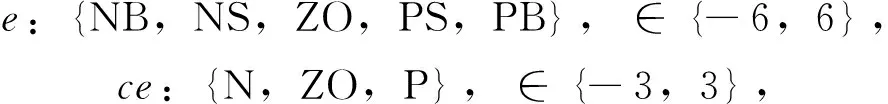
偏差e与偏差的变化率ce对应的隶属度函数分布如图3所示。

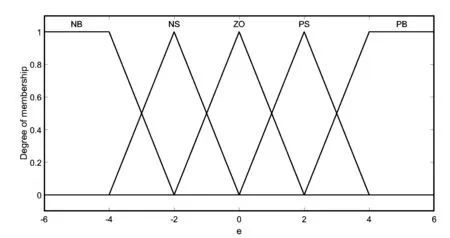
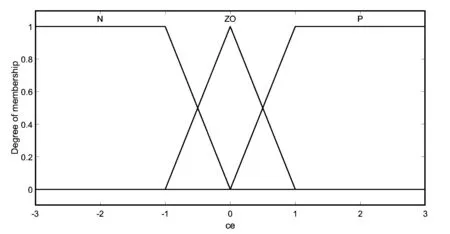
图3 偏差e,偏差的变化率ce的隶属度函数

2.4 T-S模型模糊规则

根据电子节气门常规PID的成功控制经验、多次仿真试验调整，制定了以下模糊规则：当e比较大时，为了加快系统响应速度，应选取较大的kp和较小的kd。当e和ce中等大时，为减小系统超调应选取较小的kp和适中的kd。当e和ce较小时，应选取适中的kp和kd。通过多次仿真试验最终确定kp=20，kd=5。

R1=ifeisNB andceisN,thenu1=2kpe+0.2kdce

R2=ifeisNB andceisP,thenu2=1.5kpe+0.2kdce

R3=ifeisNS andceisN,thenu3=0.8kpe+0.4kdce

R4=ifeisNS andceisP,thenu4=0.5kpe+0.5kdce

R5=ifeisZO ,thenu5=kpe+kdce

R6=ifeisPS andceisN,thenu6=0.5kpe+0.5kdce

R7=ifeisPS andceisP,thenu7=0.8kpe+0.4kdce

R8=ifeisPB andceisN,thenu8=1.5kpe+0.2kdce

R9=ifeisNB andceisP,thenu9=2kpe+0.2kdce

3 仿真验证

实验仿真，为了验证控制器的优越性，选择常规PID控制作对比仿真试验。其中，PID控制器参数为kp=50,ki=5,kd=0.2，T-S型模糊PID控制器积分系数ku=10，角弧度转换因子Kin和Kout分别为0.017 4和57.325。其仿真模型如图4所示。电子节气门模型参数如表1所示。

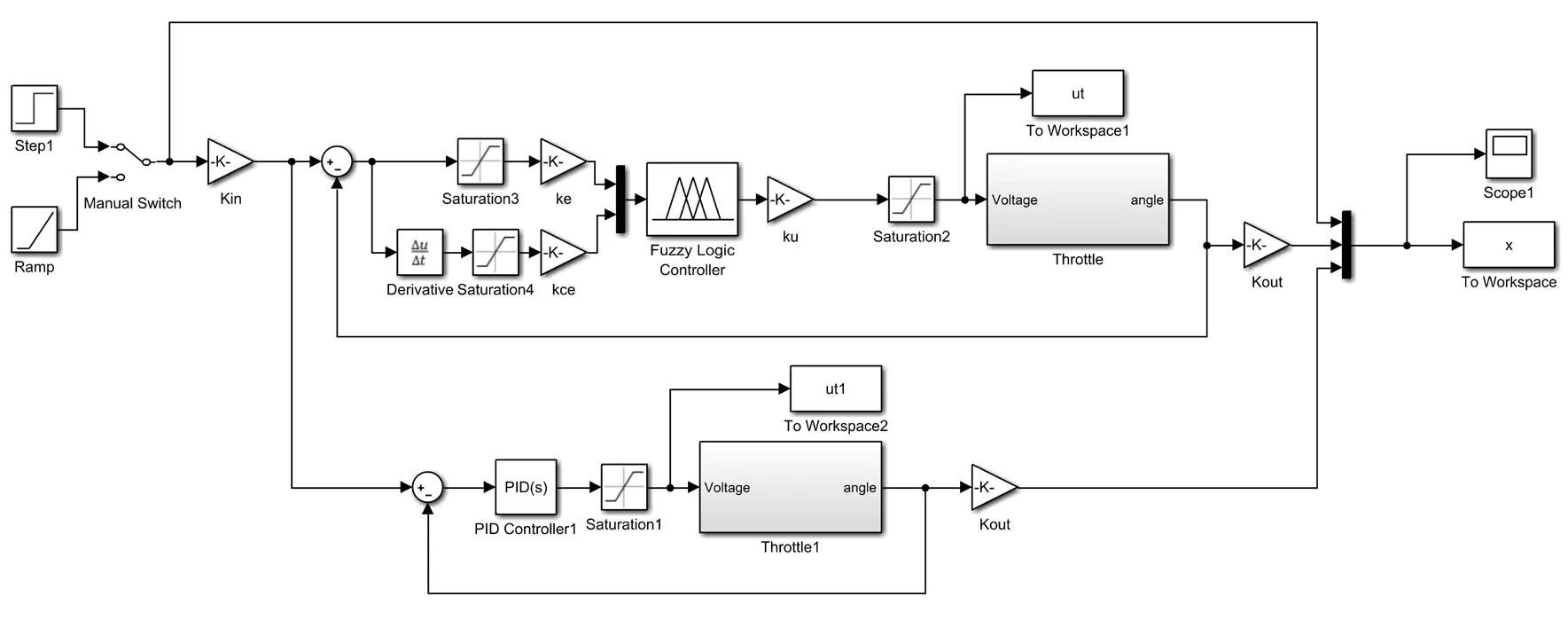
图4 基于T-S模型的模糊PID控制仿真

表1 模型参数

实验一：设节气门阀片当前位置为10°，输入目标开度为10°～90°的阶跃信号，响应曲线如图5所示。从图5中可以看出，PID控制和T-S型模糊控制在0.1 s-0.17 s的响应速度基本相同，PID控制调节时间为240 ms，超调为6.27%，稳态误差0.13。T-S型模糊控制，调节时间为152 ms，超调为0%，稳态误差0.05，且有效地抑制了振荡。

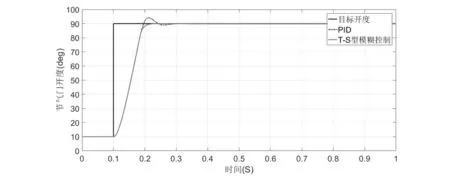
图5 90°阶跃响应曲线

实验二：设节气门阀片当前位置为0°输入斜坡信号，响应曲线如图6所示。受电子节气门复位弹簧组非线性扭矩的影响，当阀片运动到初始位置10°(坡行回家位置)时，常规PID控制会发生偏移，偏差约为1.19°，T-S型模糊控制则可以很好地跟踪上目标信号。

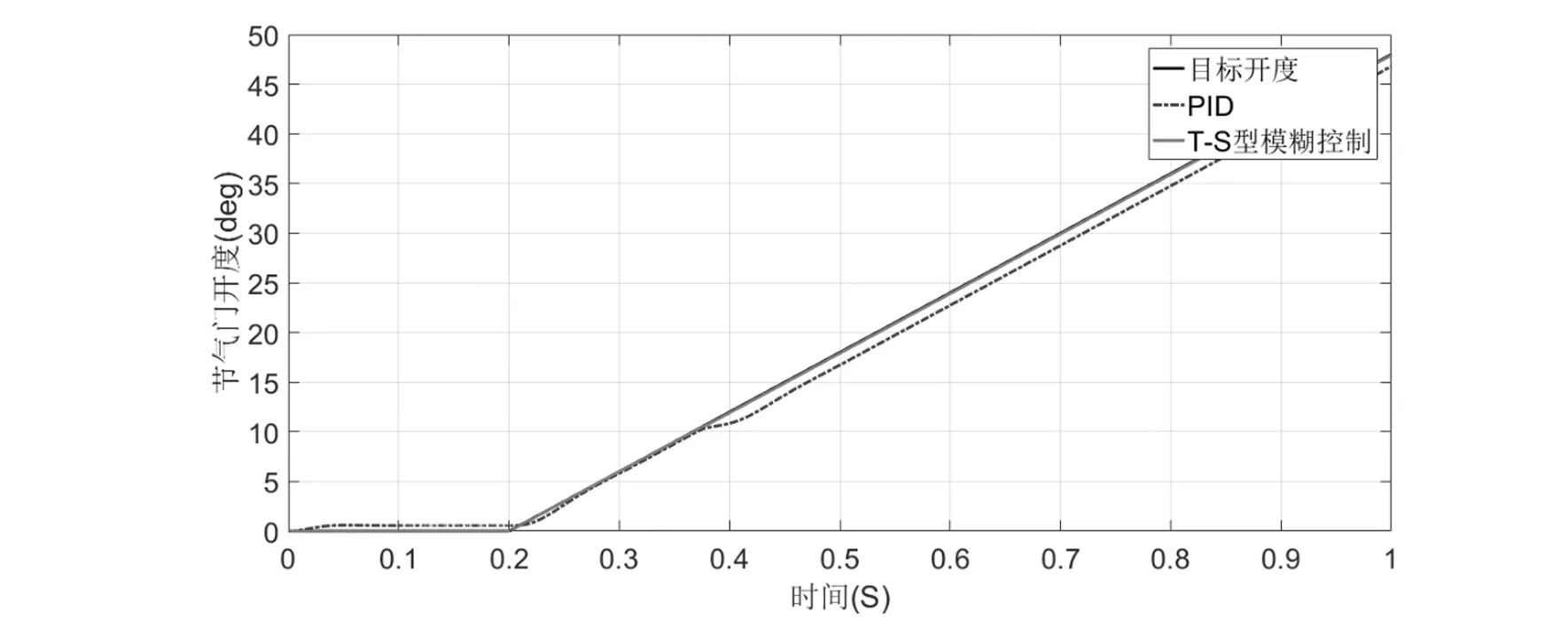
图6 斜坡信号跟踪响应曲线

实验三：输入10°～90°的阶跃信号，在0.5 s后突加1 N·m的负载扭矩扰动。响应曲线如图7所示，受到扰动后PID控制出现了较大的偏移，偏差约为4.23°。T-S型模糊控制出现了较小的偏移，偏差约为0.2°。仿真结果表明T-S型模糊控制有较强的鲁棒性，抗干扰能力更强。

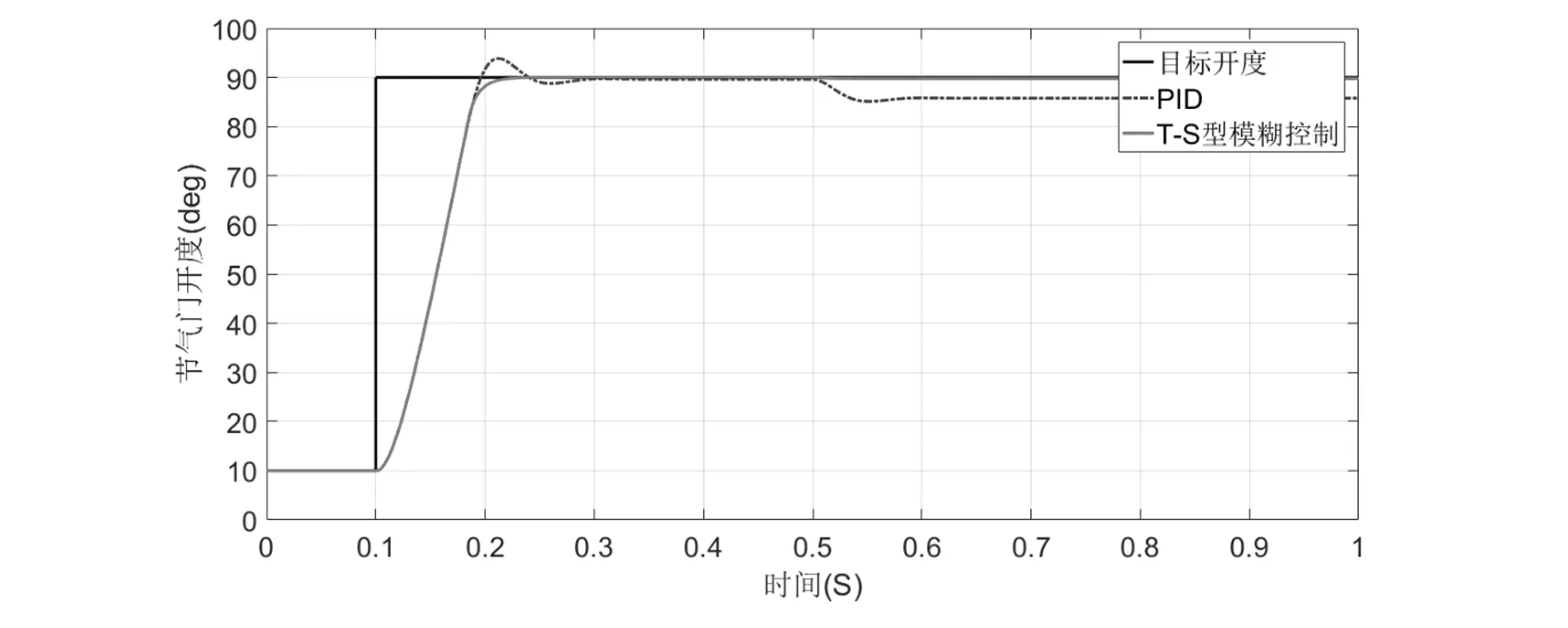
图7 角度跟踪响应曲线

从三次仿真结果看，基于T-S模型的模糊控制器有较好的静态控制性能指标和良好的动态跟踪性能，调节时间更短，震荡次数更少，稳定性更好，抗干扰能力和鲁棒性更强。但是这些良好的性能指标是以控制模型为调节对象实现的。实际电子节气门控制要复杂得多，包括参数摄动和多种外界扰动等，所以还需要考察实际应用效果。

4 结语

基于T-S模型的模糊控制方法可以有效地解决电子节气门控制系统的非线性问题，针对外界扰动有着较强的抗干扰能力，鲁棒性更好，明显改善了系统的静态控制指标。与PID和Mamdani型模糊控制方法相比有着更好的跟踪特性和更简单的结构，降低了计算成本，控制精度更高。