旋转式三维编织预制件的计算机模拟
肖田华,孙志宏,顾生辉,王振喜
(1. 东华大学 a.机械工程学院;b.纺织装备教育部工程研究中心,上海 201620;2. 航宸石家庄新材料科技有限公司,河北 石家庄 051430)
旋转式三维编织工艺源于五月柱编织,通过增加编织纱线的组数以及控制纱线运动轨迹来实现三维立体织物的编织成型[1]。与纵横编织工艺相比,旋转式三维编织效率高,更易于自动化控制,且织物编织结构的可设计性更强[2],通过给定不同的锭子初始排布序列及运动规律,可得到不同的编织结构。
针对三维编织预制件编织结构的建模问题,李毓陵[3]以编织图和方格阵描述四步法编织运动过程中锭子的位置置换,邵将等[4]在此基础上建立锭子运动的数学模型并结合SolidWorks软件得到织物编织结构的实体模型,张小萍等[5]在分析二步法编织运动规律和纱线空间屈曲形态的基础上建立纱线及编织物的三维模型;马文锁等[6]用点群、点阵和空间群推导得到三维空间纱线交叉几何结构。现有的三维织物编织结构建模研究主要集中于纵横编织工艺,对于旋转式三维编织预制件编织结构的建模,现阶段还未见文献报道。
本文以轨道拼接的旋转式三维编织工艺为研究对象,建立编织过程中锭子位置变换与变轨装置状态对应关系的数学模型,并利用计算机编程对编织纱线的运动路径进行模拟,结合图形软件构建纱线运动轨迹的实体模型,从而完成对织物结构的模拟。
1 旋转式三维编织设备
旋转式三维编织设备[7]可分为Tsuzuki式、3TEX式和Herzog式,其主要区别为锭子在相邻叶轮交会处的运动方式不同。
Tsuzuki式[8]三维旋转编织设备底盘如图1(a)所示,底盘上装有叶轮和锭子,相邻叶轮交会处仅放置一个锭子,在编织过程中相邻行或列的叶轮反向间隔转动,以此驱动锭子到达下一个位置。 3TEX式三维旋转编织设备底盘如图1(b)所示,其叶轮交会处增加了可活动的变轨装置。叶轮与变轨装置由不同的动力系统驱动,在编织过程中相邻行或列的叶轮同时转动,且每转动90°后会暂时停止,等待变轨装置旋转180°交换两边的锭子,紧接着叶轮继续转动,从而驱使锭子以步进的方式运动。为提升编织过程中锭子的运动速度,同时防止锭子间产生干涉,在3TEX式设备编织底盘的基础上,通过减少一半数量的锭子排布,并在叶轮上留出一半槽口空位,得到Herzog式设备编织底盘,如图1(c)所示,其在编织时可对变轨装置状态进行控制,以此实现轨道的动态拼接,从而确定锭子在叶轮交会处的运动轨迹。表1列举了3种编织设备的各项性能,Herzog式编织设备的生产速度最高可达25 m/h[1],相比其他两种编织设备,其编织效率提升了约30%。

(a) Tsuzuki

(b) 3TEX (c) Herzog

表1 三种编织设备的性能对比
2 轨道拼接式编织工艺
本文以Herzog式三维编织设备为研究对象,对轨道拼接式编织工艺进行分析,其编织底盘为4×4叶轮组合,如图2所示。在相邻两个叶轮间布置一个变轨装置,变轨装置的状态如图3所示,并引入“0”“1”对其进行描述[9],“1”对应“×”(交会处连通),“0”对应“∥”(交会处未连通)。根据实际的编织需求切换变轨装置的状态,完成轨道的动态拼接,进而改变编织纱线的运动轨迹,实现对各类截面织物的编织成型。

图2 4×4编织底盘Fig.2 4×4 braided chassis
在编织过程中,锭子一直处于叶轮的槽口内,并沿底盘轨道运动,假定叶轮的角速度为ω,锭子的运动速度v=ωr(r为轨道槽的半径),设叶轮转动一圈所需时间为t,锭子从一个槽口运动到下一个槽口所需时间为t/4。在两个相邻槽口的轨道上,锭子从极限位置1(锭子刚好完全出槽口)运动到极限位置2(锭子即将进入下一槽口)所对应的叶轮转角为φ,所需要的时间为φt/2π,刚好对应于变轨装置空置的时间(无负载),该段时间可用于变轨装置的位置变换,实现编织轨道的动态拼接,如图4所示。

(a) 状态“1” (b) 状态“0”

图4 锭子运动示意图Fig.4 Diagram of carrier movement
3 编织过程中锭子运动的数学模型
锭子的运动轨迹决定了织物的编织结构[10]。在编织过程中,所有叶轮的转向保持不变,锭子的运动轨迹可看作由变轨装置来控制,因此可根据变轨装置的状态与锭子位置的对应关系建立编织过程的数学模型,并对锭子的位置变换进行追踪,获得完整的锭子运动轨迹。
3.1 锭子运动过程描述
根据轨道拼接编织原理,建立锭子与变轨装置坐标系,如图5所示。由图5(a)可知,每个叶轮有4个槽口,可同时在半数槽口上放置锭子,在叶轮的A、B、C、D各处都有一变轨装置,锭子每经过一次变轨装置,位置坐标都要变换一次。例如:叶轮I槽口2上的锭子在经过B处变轨装置后可进入叶轮II的槽口4,锭子位置坐标由(2,1)变成(3,2),对应B处的变轨装置的状态为“1”;也可进入叶轮I的槽口3,锭子位置坐标变换为(2,2),B处变轨装置的状态为“0”。

(a) 锭子坐标系

(b) 变轨装置坐标系
为更清晰地描述锭子在运动过程中的坐标变换情况,对叶轮进行区域划分,在每个区域上设定对应数值+1或-1,以表示锭子位置坐标的变换情况。叶轮自正转情况如图6(a)所示,槽口4的锭子经过A处变轨装置到达槽口1,其y坐标不变,x坐标值为+1, 正好对应于槽口1区域的设定值+1。在图6(b)所示的叶轮自反转情况中,锭子从槽口4经D处变轨装置达槽口3,其x坐标不变,y坐标为+1,对应于槽口3区域的设定值+1。图6(c)表示多个叶轮的组合情况:当锭子从正转叶轮I的槽口3经G处变轨装置到反转叶轮IV的槽口1,其对应的坐标变换情况是x坐标为-1,y坐标为+1,目标区域的设定值-1与x坐标变换值对应,原区域的设定值+1与y坐标变换值对应;当锭子从反转叶轮IV的槽口3经F处变轨装置到正转叶轮III的槽口1,其对应的坐标变换是x坐标为+1,y坐标为-1,目标区域的设定值-1与y坐标值对应,原区域的设定值+1也与x坐标值相对应。
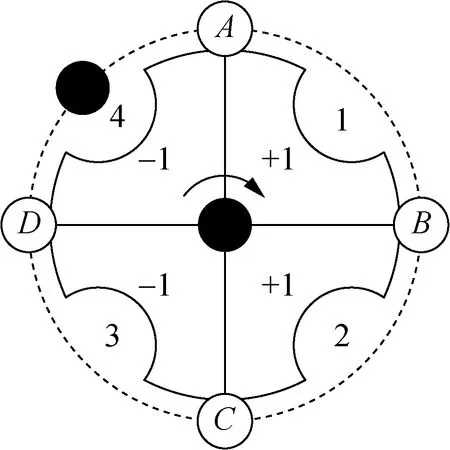
(a) 自正转

(b)自反转

(c)组合
根据上述不同情况的描述,归纳总结出叶轮上各区域的设定值与锭子坐标变换的对应关系。当锭子在单个叶轮上运动时,每经过一次变轨装置,只有一个坐标值发生变换,且变换值为叶轮目标区域的设定值。同时可根据变轨装置所处的位置得出,奇数行的变轨装置对应的是y坐标变换:偶数行的变轨装置对应的是x坐标变换;当锭子在多个叶轮组合情况下运动时,正变换(由正转叶轮过渡到反转叶轮上)目标区域的设定值与x坐标变换值对应,原区域的设定值与y坐标变换值对应;而逆变换的情况刚好与正变换相反。
3.2 锭子坐标变换的数学表达
为方便对编织过程中锭子坐标变换情况进行建模分析,引入锭子的位置坐标矩阵I(k),如式(1)所示。
(1)
式中:Imn以复数m+ni表示,其中m、n分别对应锭子所处位置的x、y坐标值;k表示编织步骤。
以图6(c)中的叶轮组合为例,锭子的起始位置坐标矩阵(k=0)可表示为式(2)。

(2)
在前文中已对变轨装置的状态进行“0”“1”划分。当变轨装置状态为“0”时,轨道交会处未连通,对应锭子只有x或y坐标发生变换;当对应状态为“1”时,锭子x和y坐标都发生变换。现有变轨装置的两个状态对应值无法完整描述编织过程中变轨装置对锭子坐标变换所起的作用。在此借助叶轮上各区域的设定值,定义变轨装置的状态矩阵H(k)如式(3)所示。
(3)
式中:0表示该处无变轨装置;其他项Hp(q-1)=c+vi表示p、q的值与叶轮的行、列数有关,具体为2倍叶轮行、列数加1,c、v的值与锭子经过变轨装置后x、y坐标的变换值相对应。以图6(c)中锭子的起始排列情况为例,对应变轨装置状态矩阵如式(4)所示。
(4)
式中:H21=1;H12=-i;H32=1+i。
由于锭子位置矩阵I(k)与变轨装置状态矩阵H(k)的维数不相同,为方便计算将I(k)、H(k)按叶轮单元进行划分,如图7所示,计算时将两类单元矩阵上位置相同的元素进行相加运算,得到锭子在每一编织步骤中的位置变换情况。
单个锭子在编织运动中的坐标变换的递推如式(5)所示。
I(k)[m,n]=I(k-1)[m,n]+H(k)[c,v]
(5)

图7 矩阵I(k)、H(k)单元划分方案Fig.7 Division scheme of matrix I(k)and H(k)
在经历若干编织步骤后,锭子会回到运动起始点,即
I(T)[m,n]=I(0)[m,n]H(k)[c,v]
(6)
式中:T为锭子运动周期。锭子的编织模式可用矩阵I(k)、H(k)累加表示,k从1取到T。
根据以上分析,在给定锭子的初始位置矩阵以及变轨装置的状态矩阵即编织模式后,锭子的运动规律得以确定,织物编织结构也随之确定。
4 织物结构的计算机模拟
本文对轨道拼接的旋转式三维编织预制件进行计算机模拟的流程如图8所示,并以实体分支结构预制件为例,建立编织结构模型。
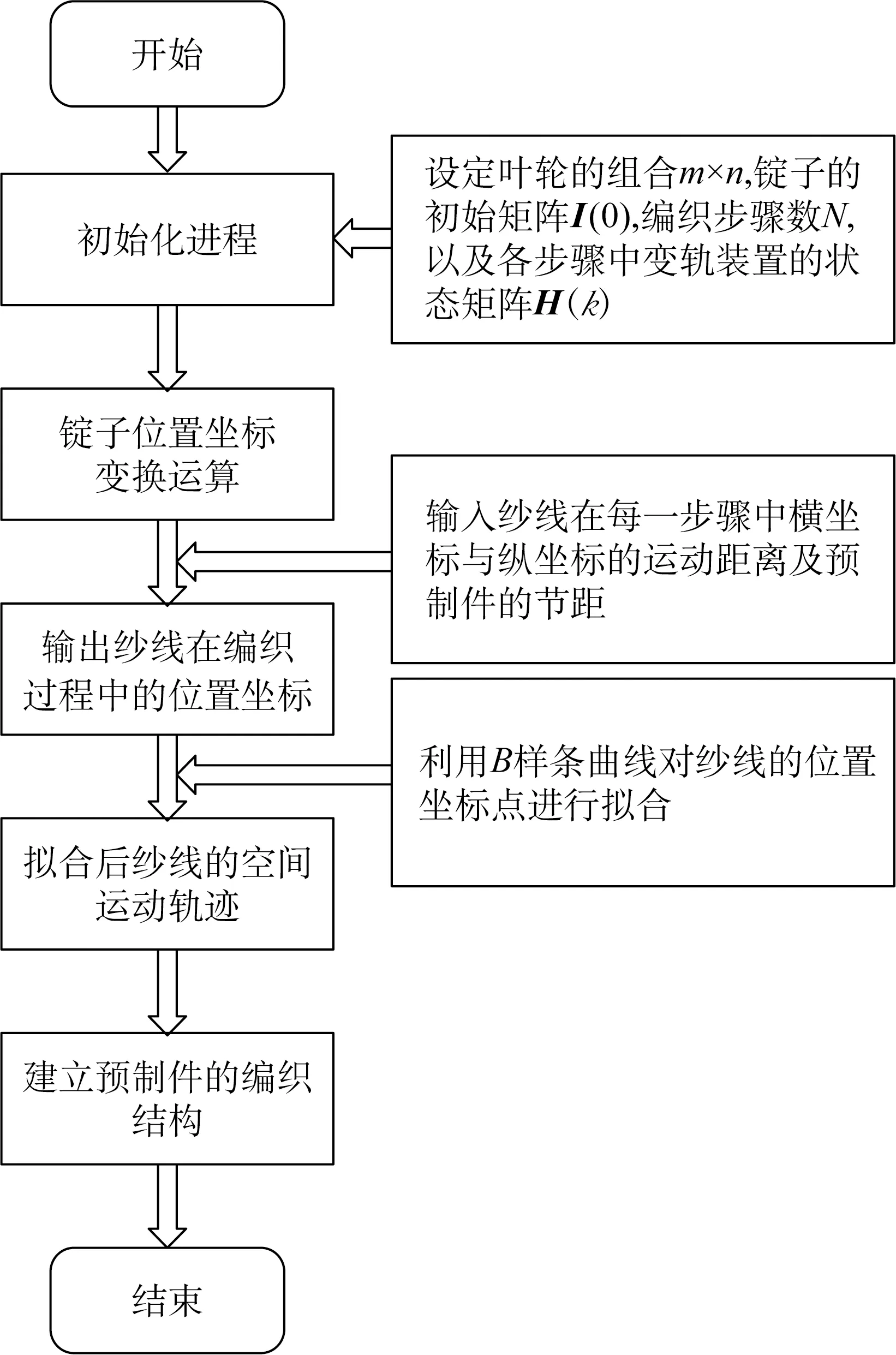
图8 编织结构建模流程图Fig.8 Simulation system flow chart of braided structure
分支编织是将整体织物“一分为二”,整个编织过程是连续进行的,只需动态地改变某些步骤中变轨装置的状态矩阵,从而改变纱线的交织结构。2×4的叶轮组合如图9所示,锭子位置坐标的初始矩阵I(0)如式(7)所示。

图9 分支编织的2×4编织原理图Fig.9 Schematic diagram of 2×4 branch braiding

(7)
实际编织过程可分为以下步骤:
未进行分支编织时,当设定k为奇数时,变轨装置的状态矩阵H(k)如式(8)所示。
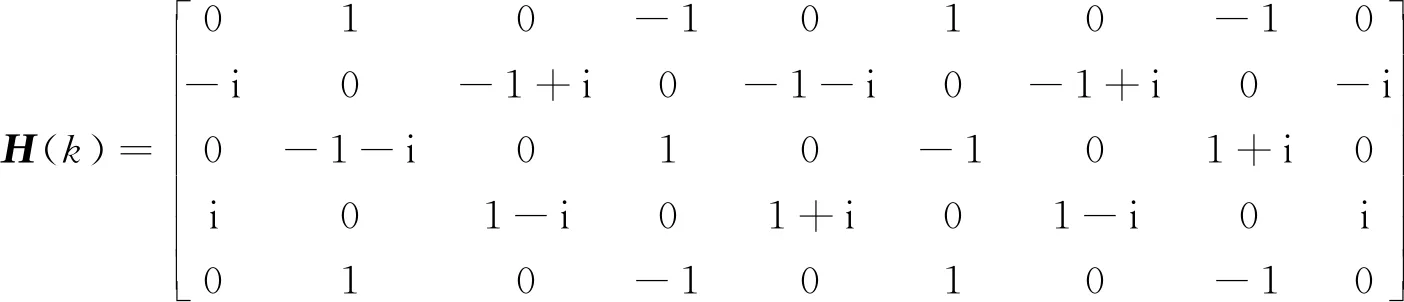
(8)
未进行分支编织时,当设定k为偶数时,变轨装置的状态矩阵H(k)如式(9)所示。

(9)
为避免进行分支编织时锭子间产生干涉,需要调整变轨装置的状态以调整锭子的序列,该过程为过渡编织对应的变轨装置状态矩阵H(k)如式(10)所示。
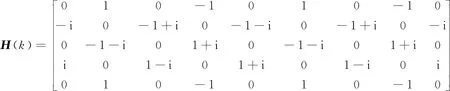
(10)
在编织分支部分时,当k为奇数时,变轨装置状态矩阵H(k)设定如式(11)所示。

(11)
在编织分支部分时,当设定k为偶数时,变轨装置状态矩阵H(k)如式(12)所示。

(12)
在各编织步骤中,变轨装置状态矩阵的奇、偶取值与锭子的初始位置有关。根据锭子坐标变换与变轨装置状态的对应关系,用MATLAB软件编写纱线空间轨迹点的计算程序[11]。通过设定目标参数计算编织纱线空间位置的数据拟合点,得到相应的数据文件。以SolidWorks软件为三维仿真平台,导入纱线的数据文件以生成编织纱线的空间运动轨迹。假定在编织过程中纱线截面不发生变化且一直为圆形(此处纱线截面半径r设为1 mm),且圆心在拟合后的纱线空间轨迹上移动。绘制出每根纱线的实体结构,进而得到分支结构织物的三维实体模型,实现Herzog式三维旋转编织预制件的计算机模拟。
为了验证本文中编织结构模拟的正确性,设计了900 mm×1 000 mm×2 000 mm的Herzog式编织设备的虚拟样机,如图10所示。该设备最大可挂载128根纱线。图11(a)是分支实体预制件的模型,图中H是整体部分的花节长度,h是分支的花节长度;图11(b)是分支预制件的编织实物。将模型各部分的花节长度与实际编织物进行对比可知,本文所建立的分支结构模型与实体编织结构非常贴合,说明本文提出的模拟方法是切实可行的。

注:1—底座机架;2—主体部分;3—牵引部分。图10 编织设备虚拟样机Fig.10 Virtual prototype of braided machine

(a) 模型

(b)实物
5 结 语
本文以轨道拼接的旋转式三维编织工艺为研究对象,利用矩阵表示锭子的位置坐标和变轨装置的状态,以矩阵运算来表示编织过程中锭子的坐标变换,据此建立相应的数学模型。为验证上述方法的正确性,利用MATLAB软件编写程序获得各步骤中锭子运动坐标的数据库,并结合SolidWorks软件实现编织物结构的计算机模拟。该方法所建立的织物模型与实际编织结构中纱线运动轨迹完全相同,可为后续对旋转编织预制件力学性能的分析研究奠定基础。

