基于滑模控制的车辆自适应巡航系统设计

张立发，赵秀春，高天一

(大连民族大学 机电工程学院，辽宁 大连 116605)

自适应巡航控制(Adaptive Cruise System，ACC)是汽车智能驾驶辅助系统(Advanced Driver Assistance System，ADAS)的重要组成部分[1-2]。该系统能够使驾驶者自动调节节气门开度和制动压力，不仅减轻了驾驶员的驾驶负担，而且减少了驾驶者的操作失误，对提高车辆驾驶安全性具有重要作用[3]。根据美国交通运输部门的统计数据，在交通运输中使用ACC系统，高速公路上行驶的车辆接近减速状态的前车时，追尾发生率可降低15%以上，在超车、换道等常见情况中也能有效降低事故发生的概率[4-5]。在汽车智能化、网联化、电动化的大趋势下，ADAS带来的舒适、安全的驾驶体验被越来越多的消费者所接受，市场应用比例逐年上升。

目前，国内外科研院校对ACC系统开展了富有成效的研究。在实际的应用控制中，PID控制与滑模控制仍然占据着主流地位。PID控制虽然控制机理完全独立于对象的数学模型，只用控制目标与被控对象实际行为之间的误差来产生消除此误差的控制策略，在工程实践中得到广泛应用。文献[6]采用经典PID控制算法进行速度跟踪控制；Yi K和Hong J等[7]将前馈控制与PI反馈控制相结合，对车辆纵向模型进行速度与距离的控制；Stanley等[8]运用较为简化的PI进行自适应巡航控制研究；Shakouri等[9]分别设计了增益调度的PI和线性二次型调节(linear quadratic regulator，LQR)两种控制器来控制节气门开度，其中LQR依赖于准确的模型，当模型失配时会导致控制器性能退化；王文飒等[10]提出了基于深度强化学习的协同式自适应巡航控制策略，对车辆的控制效果有较大提升，但算法编写复杂，实时应用存在一定难度；李世豪等[11]和李肖含[12]均提出基于模糊PID控制的自适应巡航控制策略，该策略在简单路况下控制效果较好，但在复杂路况下控制效果难以保证。虽然PID控制应用简便、广泛，但控制器参数值不能随路况及时调整，即使可通过加入逻辑模糊工具箱实时参数值调整改善PID控制性能，也由于模糊规则是根据驾驶者经验制定，缺乏定量的评价方法。模型预测方法能够利用状态进行模型预测实现实时控制而被采用[13]，但其模型较为复杂且适应性不高。基于上述情况，本文提出一种基于滑模控制(Sliding Mode Control，SMC)的自适应巡航系统控制策略，利用SMC鲁棒性强、对外界扰动不敏感等特点提升ACC系统的控制效果，以提高其在复杂跟车环境的适用性。

1 系统模型

车辆跟踪系统示例如图1，其中pi、pq分别为当前车辆i与前车q的位置和速度，假设车辆已经配备了V2V等无线通信传感装置，能够获取前方车辆的状态信息。

图1 车辆跟踪系统

车辆的纵向动力学：

(1)

(2)

式中：mi、pi、vi分别为当前车的质量、位置和速度；Fi为汽车的牵引力，Fa为汽车行驶过程中的空气阻力，由汽车行驶速度vi、空气阻力系数CD、空气密度ρ和车辆迎风面积A四种因素共同决定；Fr为汽车的滚动阻力；Fg为坡道阻力。

(3)

滚动阻力：

Fr=μmigcosθ。

(4)

式中：μ为滚动阻力系数；g为重力加速度；θ表示道路坡度。

车辆的坡道阻力：

Fg=migsinθ。

(5)

综合式(1)-式(5)，车辆的动力学模型为

(6)

(7)

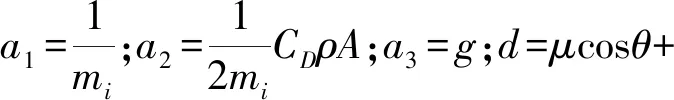
理想的车间距定义为

dc=pq-pi-ki。

(8)

式中：dc为理想的车间距，即在当前最高限速下制动且不与前方车辆相撞的最小安全距离；pq表示前车的位置；pi表示当前车的位置；ki表示车身长度，这里为了模型的简化可以忽略车身长度。

补充说明：理想的车间距dc多采用固定值[14-15]，而文献[16]采用基于车速变化而设定dc，往往由于车速实时变化使得安全距离不断地变化从而影响控制性能。为了简化模型并且避免由于安全距离的不断变化导致的安全隐患，本文假定在同一路段车速限速不变的情况下采用固定的车间距。

2 滑模控制器的设计

针对汽车动力学系统，考虑速度的跟踪控制，由式(5)设计滑模控制器如下。

定义车辆的跟踪误差：

e(t)=pq-pi；

(9)

对式(9)求导，

(10)

考虑滑模面：

(11)

式中，参数c必须满足Hurwitz条件，即c>0。

(12)

选择指数趋近律：

(13)

式中：控制器参数D表示系统运动点向切换面趋近的速率，D>0;k表示收敛速度，k>0。

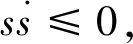
(14)

为分析自适应巡航控制系统的稳定性，选取Lyapunov函数：

(15)

对其求导，并将式(12)、式(14)代入，

=s(-ks-Dsgn(s))

(16)

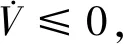
(17)

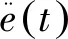
3 仿真验证

针对上述车辆滑模控制自适应巡航系统应用Matlab进行仿真验证，并通过与PID控制的结果进行比较，验证所设计控制器的有效性。首先，考虑一般工况下，车辆经过加速—恒速—减速的工况进行研究。假设前车工况通过智能交通系统可以获得，设定车辆安全距离为20 m，滑模自适应巡航控制器参数分别选取：c=6，k=5，D=5。车辆主要参数见表1。

前车与采用不同控制方法下的车辆位置、速度与加速度曲线如图2-图4。通过PID控制与SMC控制进行对比，可以观察到两种控制均能实现车辆自适应跟踪控制，但本文所设计的控制器具有更快的加速度响应，速度跟踪性能更优。

表1 车辆主要参数

图2 车辆位移曲线

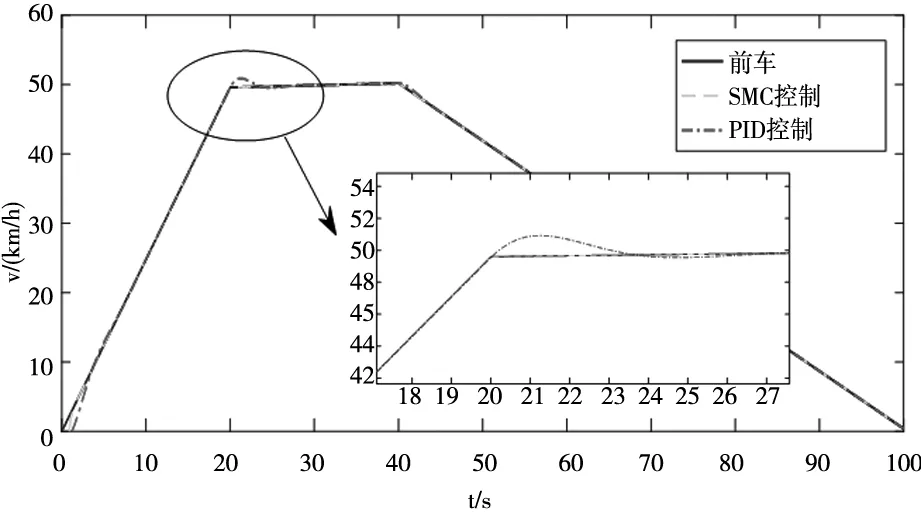
图3 车辆速度曲线

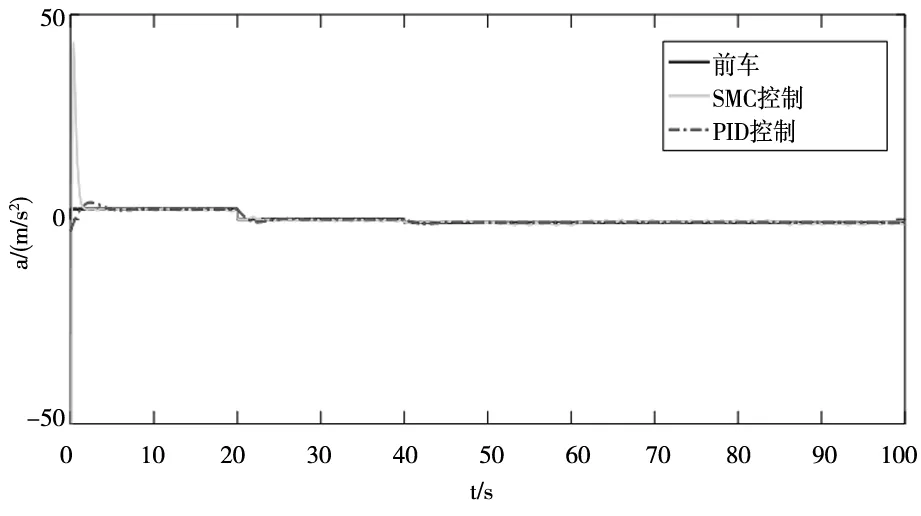
图4 车辆加速度曲线

为了研究控制器的抗干扰能力，假设系统存在扰动如图5，仿真结果如图6-图7。在存在扰动的情况下，滑模控制通过切换面的快速响应依旧可以较好地完成跟踪控制，并且鲁棒性较强，PID控制虽然也可以完成速度与加速度的跟踪，但鲁棒性较差，存在较大的抖动。由此可以看出本文采用的方法具有良好的鲁棒性。

图5 车辆扰动

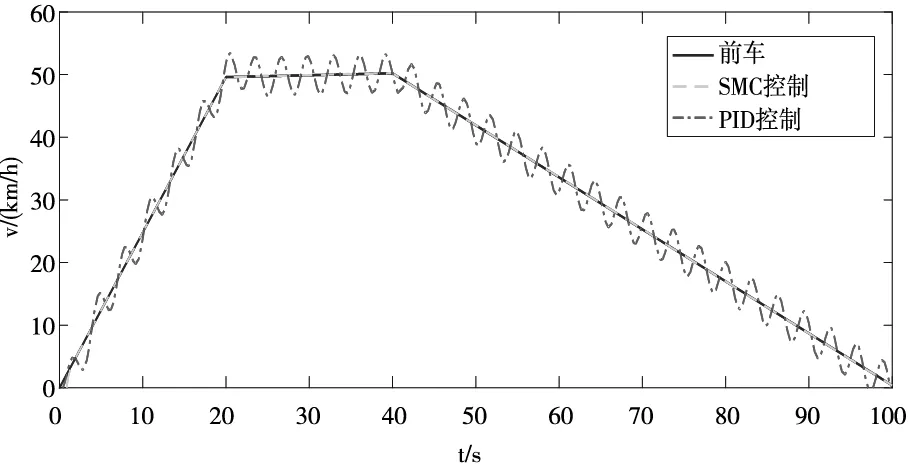
图6 存在扰动下的车辆速度

图7 存在扰动下的车辆加速度

最后，在城市ECE工况下与PID控制器对比，仿真结果如图8-图10。

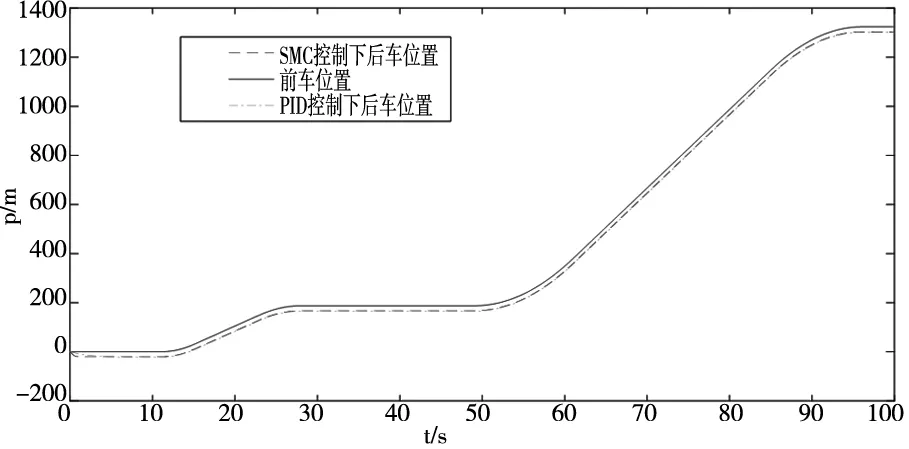
图8 ECE工况下车辆位移曲线

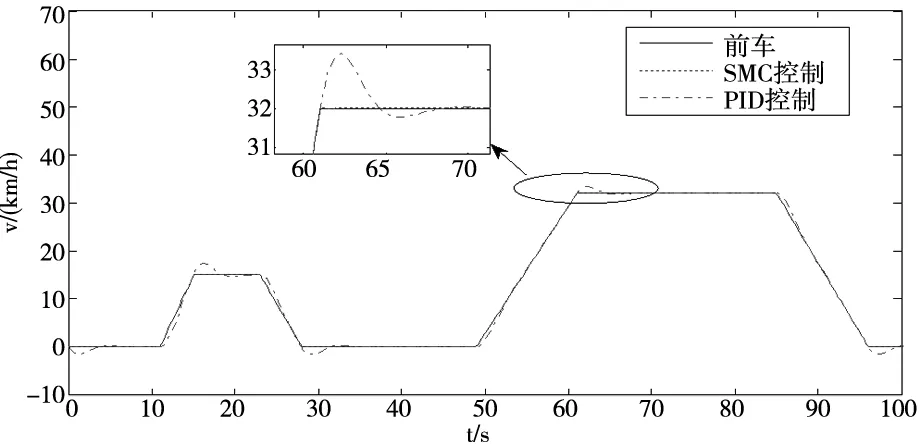
图9 ECE工况下车辆速度曲线

图10 ECE工况下车辆加速度曲线

通过局部放大，可以看到SMC控制下车辆速度几乎与前车保持一致，SMC控制通过切换面具有更快的响应速度，进行加速度的快速调整实现自适应巡航系统的快速响应，具有更加理想的跟踪性能，也更好地适应了工况的变化。

4 结 论

本文研究了车辆自适应巡航控制系统，考虑在不同路况和存在扰动的情况下，基于安全车距设计了自适应巡航滑模控制器，并进行了稳定性分析。通过与PID控制进行对比仿真研究，考虑一般工况、存在扰动和ECE城市工况三种情况，结果表明，所设计的滑模控制器具有更快的收敛速度和响应时间，也表现出了更好的抗干扰能力，能够在保证安全距离的前提下，展现更好的跟踪性能与适应工况变化的能力。