基于峰度检验和小波包分解的海洋平台脉冲噪声处理方法研究

李 伟，黄 焱

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300350；2.天津大学 建筑工程学院，天津 300350；3.天津大学 港口与海洋工程天津市重点实验室，天津 300350)

海洋平台作为海上生产和生活的基地[1]，为了确保平台安全作业，对平台结构进行实时健康监测，及时辨识损伤并对结构状态进行评估与预警，具有重要的工程意义。这一方法需要在结构服役期间以传感系统采集结构的动态响应，通过动态响应提取损伤敏感性特征进行统计分析，进而判定结构的健康状况。考虑到腐蚀性盐水环境会对传感器造成不良影响，极易造成传感器的损坏，因此，振动传感器通常安装在平台甲板上[2]。

虽然将传感器布置于平台甲板对提高传感器的寿命以及控制结构健康监测的成本起到了积极的作用，然而平台上的很多设备都布置于甲板位置，包括钻井与井口设备、油气处理设备等，这就致使传感器处于较为复杂的噪声环境中，振动响应信号将不可避免的受到噪声的影响。图1展示了采集得到的现场加速度时程曲线，从图中可以观察到曲线存在很多脉冲噪声，这将影响损伤敏感性特征的提取。由此可见，如何对脉冲噪声进行降噪，是数据预处理的主要内容之一。

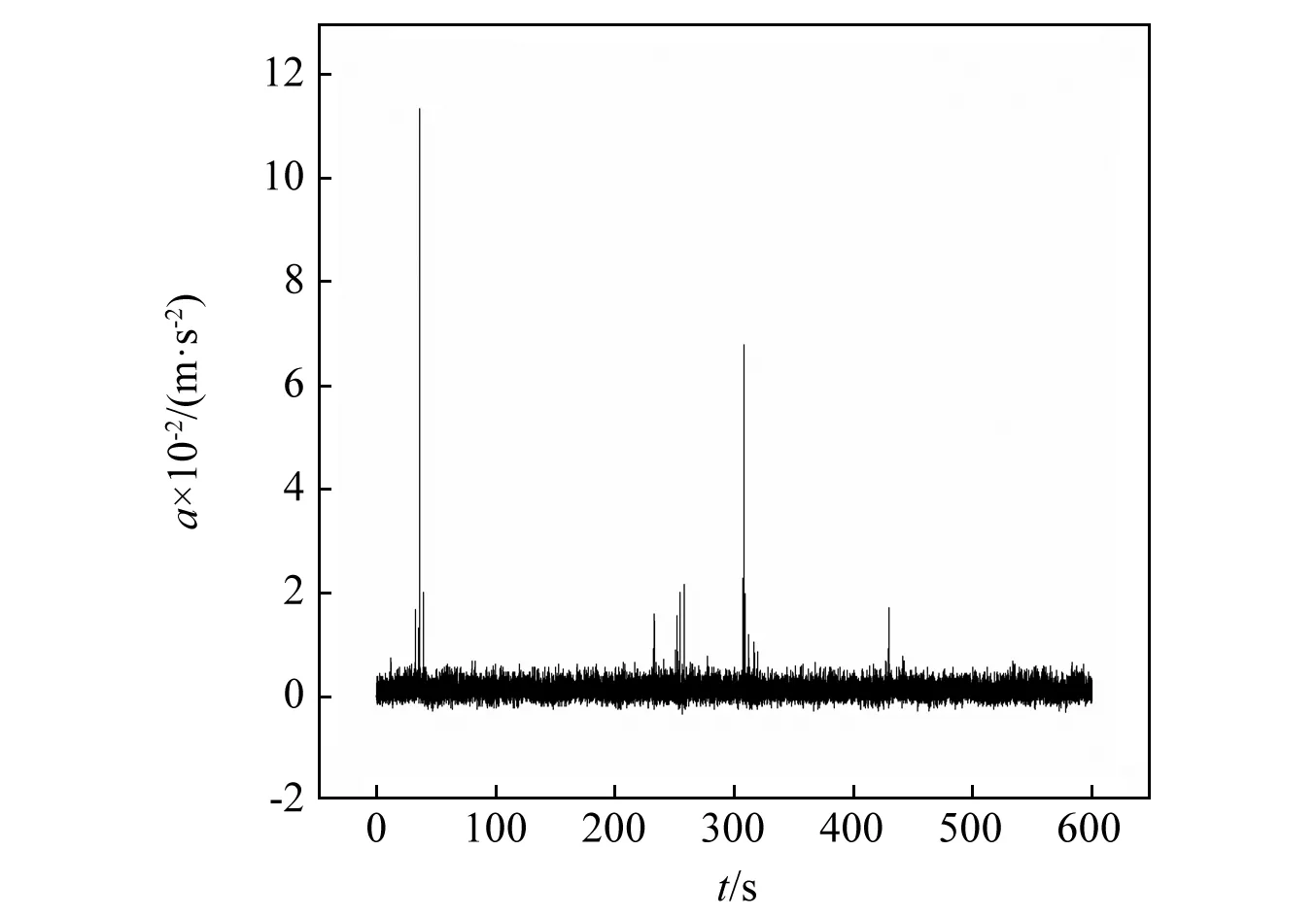
图1 现场监测加速度时程曲线Fig.1 Acceleration time history curve of field monitoring

脉冲噪声时域上的特征主要表现为振动响应值通常高于正常信号的几倍甚至十倍以上，同时噪声的频谱具有很宽的频带,往往和信号频率重叠在一起,常用的数字滤波器无法将两者区分开来[3]。童进等[4]提出了一种时域降噪方法，该方法首先确定脉冲噪声的位置,并用同相位点的平均值代替该点的值的方法消除脉冲噪声，这一方法取得了一定效果，但降噪后的曲线仍存在峰值很高的脉冲噪声。

从上述分析可以发现，仅仅依靠频域或时域的降噪方法对于脉冲噪声的处理并不十分理想，而小波包变换可以用于对信号进行时-频分析[5-6]，目前在信号处理领域取得了广泛的应用。严家斌等[7]提出了利用小波变换模极大值特性的改正方法，并利用实测数据验证了该降噪算法。何志勇等[8]在小波包域内估计脉冲噪声的能量分布并依据估计结果计算每段脉冲噪声的滤波阀值，利用这一算法对轴承故障检测的数据进行处理。但这一方法对脉冲噪声的特性有一些假设条件，不适用于较为复杂的脉冲噪声。尽管目前开展了一些基于小波包的脉冲噪声降噪方法，但对于海洋平台脉冲噪声的研究较少，因此，本文将发展一套基于峰度检测和小波包分解相结合的海洋平台脉冲噪声处理方法，并利用此方法对现场监测数据进行处理。

1 峰度检验与小波包联合降噪方法的提出

小波包变换是小波变换的进一步改进，克服了小波变换对信号的高频部分没有细分的缺点，提供了一种更为精细的分析方法。这一方法利用递归滤波操作将输出信号在由高到低的较宽频带上同步连续分解，根据频带的变化自适应的确定信号分辨率的取值，形成既有低频又有高频的能量组成[9]。小波包变换应用于信号降噪的基本思想是未受噪声污染的信号和噪声信号的小波包系数具有不同的小波包变换特性。幅值较大的小波包系数代表未受噪声污染信号的信息，幅值较小的小波包系数代表噪声信号的信息。通过合理的阈值设置可以调整较大的系数，而将幅值较小的系数设置为零，随后再进行重构得到降噪后的信号[10]。

然而，传统的小波包降噪方法主要针对白噪声和宽带噪声，并且具有较好的降噪效果。对于脉冲噪声，降噪效果并不理想[11]，具体表现为噪声能量在较短的时域区间内依然比较显著，因此，如何快速寻找这些时域区间并在区间内对小波包系数进行合理的阈值量化是小波包进行脉冲降噪的技术难点。由此目标出发，本文提出了两点改进：峰度检验，即利用峰度确定脉冲噪声出现的时域区间和基于K-S检验和小波包系数概率统计的阈值设置方法。

1.1 峰度检测

由于噪声和正常信号是相对的，本文主要针对脉冲噪声的消除，因此将非脉冲成分暂视为正常信号。在工程上，通常利用峰度作为特征指标[12]，以表征振动信号中的脉冲信号，假设采集得到的数据为ai(i=1,2,3…，n)，峰度的计算式为

(1)

式中：k为峰度系数；n为信号的总采样点数；ai为第i个采样点；μ和σ分别为采集得到的数据的均值和标准差。

峰度是用于描述分布形态的陡缓程度的统计参量，正态分布的峰度为3。Kline[13]指出，当样本数据峰度的绝对值小于10时，可以认为观测变量基本服从正态分布，因此，本文在判断信号是否存在脉冲噪声时，将峰度的阈值设置为10。为了获取信号中的脉冲噪声出现的时间区域，需要对信号划分时间段以便求得各个时间段的峰度。具体方法如下：首先需要将原始信号进行Q等分，每段长度为L，用bm表示各段，记为{bm}，m=1,2,…，Q。需要注意的是，若L取值太小，原始信号的变化趋势不能较好的反映出来，会导致脉冲噪声和其它信号的混叠；若L取值太大，则对于脉冲噪声的时间分辨率较低。因此，L的取值应在两者之间进行折中。由于脉冲噪声持续时间通常较短，为了能有比较好的时间分辨率，本文将L的最大取值设置为15 s。当L取某一值时，可根据式(1)得到一系列峰度值{km}，m=1,2,…，Q。对这一系列峰度值进行统计，求得在此L值条件下的变异度Cvm，其定义为

(2)

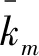
1.2 阈值选取

小波包降噪中阈值选取十分重要，依据峰度检验的结果可以确定脉冲噪声以及非脉冲信号的时间区域，因此这两类信号在每个小波包节点上映射的时域区间的小波包系数也可以相应的确定。假设第j层第k个小波包节点处的非脉冲信号对应的小波包系数G(j,k)可以表示为G(j,k)={α1,α2，α3，α4,…,αn}，对于阈值的估计，采用K-S检验来估计非脉冲信号对应的小波包系数的概率分布函数，该方法可以检验一个经验分布是否符合某种理论分布，本文考虑3种理论分布：①正态分布；②极值分布；③瑞利分布。确定了非脉冲信号段的小波包系数的分布规律后，阈值Th可根据99.7%的置信水平估计。文献[14]指出，如果脉冲噪声的小波包系数W(j,k)大于阈值Th，则将其视为脉冲系数；为了抑制脉冲，将该系数衰减为新系数W′(j,k)，由

(3)

根据式(3)的阈值修正方法，可以将某个节点脉冲噪声段的小波包系数进行修正，其它节点的小波包系数与上述处理方式类似，这里就不再赘述。对每个节点的小波包系数进行阈值量化后，再对信号进行重构，即可得到降噪后的曲线。

由此可见，基于第一点改进，可以确定脉冲噪声在每个小波包节点上映射的时域区间，基于第二点改进，可利用非脉冲信号时段的小波包系数的分布规律确定系数调整阈值，再对脉冲噪声时段的小波包系数进行阈值处理，因此，本文方法可以很好的适应脉冲噪声的时域分布，图2为本文算法的流程图，对这一方法的主要步骤进行了总结。下面将结合数值模拟的计算结果，对本文提出的方法进行应用。

图2 信号中含有脉冲噪声的降噪步骤Fig.2 De-noising procedure for time series polluted by impulse noise

2 数值模拟信号验证

2.1 数值模拟信号的获取

本文主要研究信号中的脉冲噪声消除方法，目标海洋平台是位于渤海中部海域的NB35-2平台(见图3)。该平台由导管架结构作为支撑，上部组块分为3层，平台作业水深12.6 m，平台总质量为9 610.4 t。

图3 NB35-2海洋石油平台Fig.3 The NB35-2 offshore oil platform

数值模拟信号的获取是通过在ANSYS中对导管架平台数值模型(见图4)开展相应的动力分析计算得到的，在计算中主要考虑了波流载荷的影响，为模拟各种海况下平台所受的波浪冲击，利用随机波浪理论模拟现实海况，对模型平台施加随机波浪激励。图5(a)展示了计算得到的1.0 m波高的加速度时程曲线，时间为10 min。在获得原始加速度信号的基础上，随后利用MATLAB软件生成在时域中起始位置和宽度随机的脉冲噪声，用来污染图5(a)中纯净的加速度信号，利用这一方法得到的含有脉冲噪声的信号，能够较好的检验本方法的有效性，含脉冲噪声的信号如图5(b)所示。

图4 平台有限元模型Fig.4 Finite element model of the platform

2.2 信号降噪与分析

图5(a)中的信号被脉冲噪声所干扰，为了对图5(b)中的信号进行降噪，首先应求取信号的峰度，进而得到脉冲噪声所在的时域区间。表1展示了不同L值条件下的变异度，随着L值增加变异度呈现出逐渐增加的变化趋势，在L取15时，变异程度最高，因此在进行峰度检验时，可将每段统计时间长度设置为15 s。图6展示了峰度值随时间的变化，可以观察到峰度的变化和脉冲噪声出现的时间具有很好的对应性，由此可见，利用这一指标可以准确的检测到脉冲噪声出现的时域区间。

表1 变异度随L值的变化Tab.1 Plotted results of Cvm against L

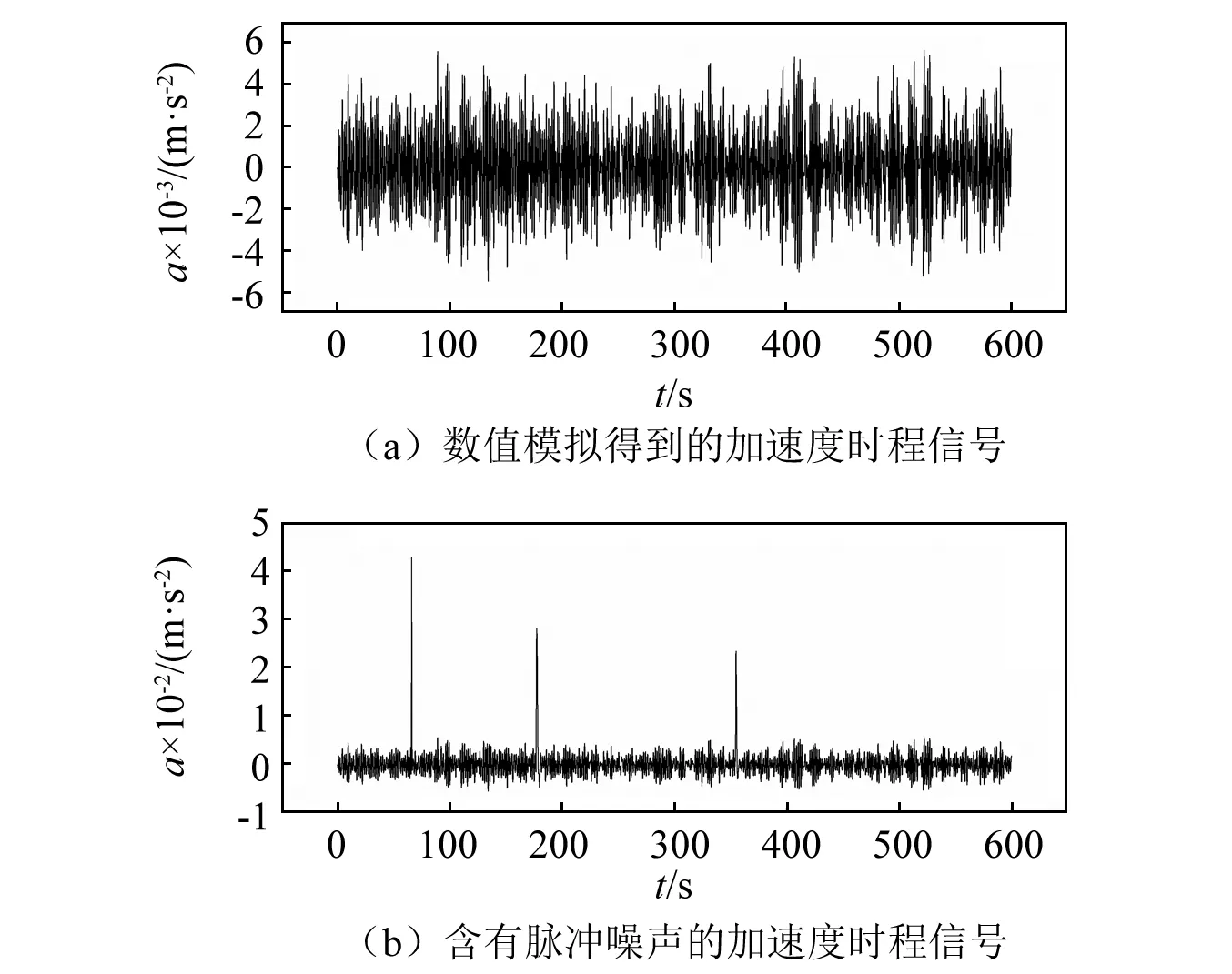
图5 加速度时程信号Fig.5 Time history of acceleration in the numerical simulation

图6 峰度检验结果Fig.6 Plotted results of kurtosis against time

峰度检验完成后，下一步将对信号进行小波包分解，采用具有多种小波基优良特性的db5小波函数进行，图7展示了经3层小波包分解后的完全二叉小波包节点树，树中节点下的数字为节点编号。经过3层小波包分解后，即可得到各个频段的小波包系数，如图8所示，展示了分解后第3层各个节点的小波包系数。从分解的小波包系数可以看到，在脉冲噪声发生的时间区域，小波包系数的绝对值较大，显著超过了非脉冲噪声信号的小波包系数。除此之外，脉冲噪声不仅影响了信号低频部分的小波包系数，同时对高频部分的小波包系数也有显著影响，这正说明脉冲噪声具有较宽的频率分布。

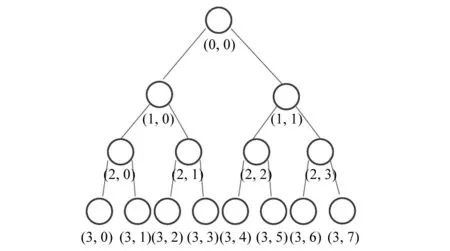
图7 三层分解的完全二叉小波包树Fig.7 Binary wavelet packet tree using 3 layer decomposition

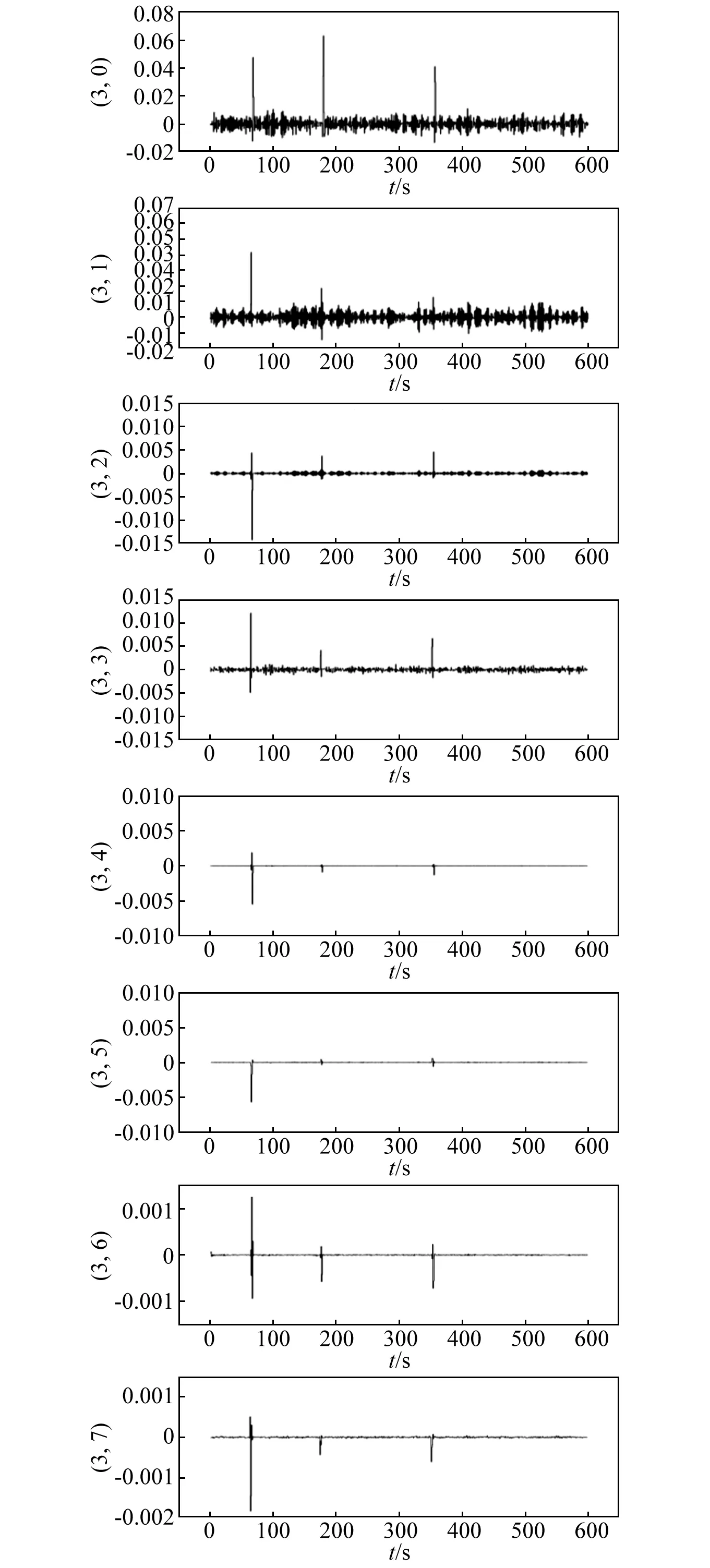
图8 第三层各个节点的小波包系数Fig.8 Wavelet packet coefficients of each node in the 3 layer

根据式(3)的阈值调整算法，需要首先对未受脉冲噪声影响的信号段的小波包系数进行K-S检验，以(3,1)节点的小波包系数为例，小波包系数较好的服从正态分布，如图9所示，因此可根据正态分布的统计规律设置这一节点的阈值为小波包系数的均值加减三倍标准差。其它节点的小波包系数的阈值设置方法也按这一节点的处理方法进行统计，从而得到各个节点的阈值。

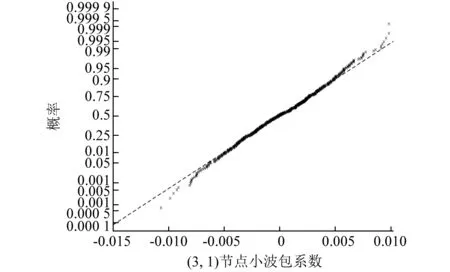
图9 (3,1)节点小波包系数正态分布概率图Fig.9 Probability plots of wavelet packet coefficients of node (3,1) for normal distribution

对各节点脉冲噪声段的小波包系数进行阈值处理后即可通过小波包逆变换重构回原始数据，结果如图10所示。从图中可以观察到，尽管脉冲导致的显著能量集中有了改善，但仍然可以从曲线中观察到脉冲噪声的迹象，这主要是由于式(3)的阈值调整方法是将幅值较大的小波包系数调整至阈值水平，这对于本文的脉冲噪声的消除不理想，因此需要进一步改进小波包系数的调整算法。

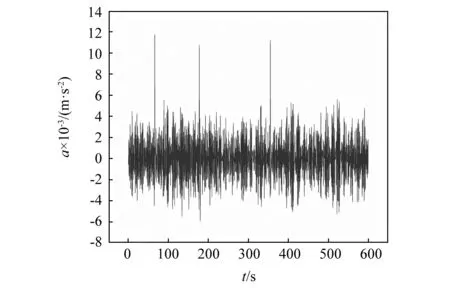
图10 数值模拟加速度时程降噪结果Fig.10 The results of de-noising for the time history of acceleration in the numerical simulation

2.3 改进方法与效果评价

当小波包系数超过阈值时，乘以一个加权函数q(j,k)[15]可使得其值迅速减小。因此，通过对脉冲噪声时段内的小波包系数进行加权，是十分重要的系数调整方法。考虑到某一节点的阈值Th和这一节点脉冲噪声时段的小波包系数W(j,k)的比值可以用来描述脉冲噪声时段的小波包系数偏离正常系数的程度，因此加权函数q(j,k)可以表示为

(4)

新的小波包系数设定方法可以在式(3)的基础上调整为

(5)

从式(5)的表达式可以看出，当脉冲噪声时段的小波包系数显著超过阈值时，经加权处理会对原始系数赋予较大的权重，而当脉冲噪声时段的小波包系数与阈值相差不显著时，加权处理后的小波包系数与阈值较为接近。经上述修正后，对调整后的小波包系数进行重构，得到的降噪曲线如图11所示，此时脉冲噪声作用的迹象已经消失，与前述的处理方法相比，降噪效果较好。

图11 新阈值条件加速度时程降噪结果Fig.11 The results of de-noising method using the new threshold

为了定量评价本文提出的降噪算法，首先定义输入信噪比(RSN,IN)和输出信噪比(RSN,OUT)

(6)

(7)

除了上述参数外，原始信号与降噪信号之间的均方根误差(root mean square error，RMSE)也是评价降噪效果的重要指标，其定义为

(8)

(9)

式中，T为信号时长。根据式(9)，选取R(τ)的最大值作为两组信号的相关性，即

(10)

由式(6)可知原始信号的信噪比(RSN,IN)为1.38，在进行算法比较时，首先根据图10的降噪结果计算上述比较参数，这一方法是Nongpiur提出的小波包阈值方法。除了这一方法外，中值滤波方法也是一种广泛采用的滤除脉冲噪声的方法，其具有计算简单以及速度快等特点，作为另外一种比较算法与本文方法进行对比，三种方法的比较结果如表2所示。从结果可以看出，本文的方法无论从信噪比还是均方根误差来说都是最好的，同时，原始信号和经本文建立的方法降噪后信号的相关系数为0.97，具有很高的相关性，降噪后的能量损失仅为3%，表明降噪后的信号是原始信号的高精度逼近。

表2 三种方法降噪后RSN，DRMSE和相关性的对比Tab.2 Comparison RSN,DRMSE and correlation of noise reduction in three kinds of method

3 现场监测信号

3.1 振动响应信号的获取

现场数据的获取主要依托“科技部十三五重大专项”的支持，利用低频加速度传感器获取NB35-2平台的振动响应，加速度传感器为德国MMF公司的KS823B系列三轴加速度传感器，每个传感器安装在防爆盒内进行保护，共在平台甲板上布置了18个传感器，数据采集频率为50 Hz。图12展示了不同测点采集得到的加速度传感器时程曲线，由图可知，在现实环境激励下，平台加速度响应时程曲线存在很多脉冲噪声。

图12 不同测点的加速度时程曲线Fig.12 Acceleration time history of different measuring points

以某一天的加速度数据为例，图13展示了各个加速度传感器一天内脉冲噪声的出现次数，图中的x轴表示时间，y轴表示传感器编号，z轴表示脉冲噪声出现次数。可以观察到，由于不同传感器处于平台的不同位置，因此每个传感器具有不同的脉冲噪声特点。同时，脉冲噪声出现频率较高的时段大致在8:00—12:00、14：00—18:00，这也正对应平台常规作业时段。由此可见，脉冲噪声的出现和平台上的生产作业息息相关。

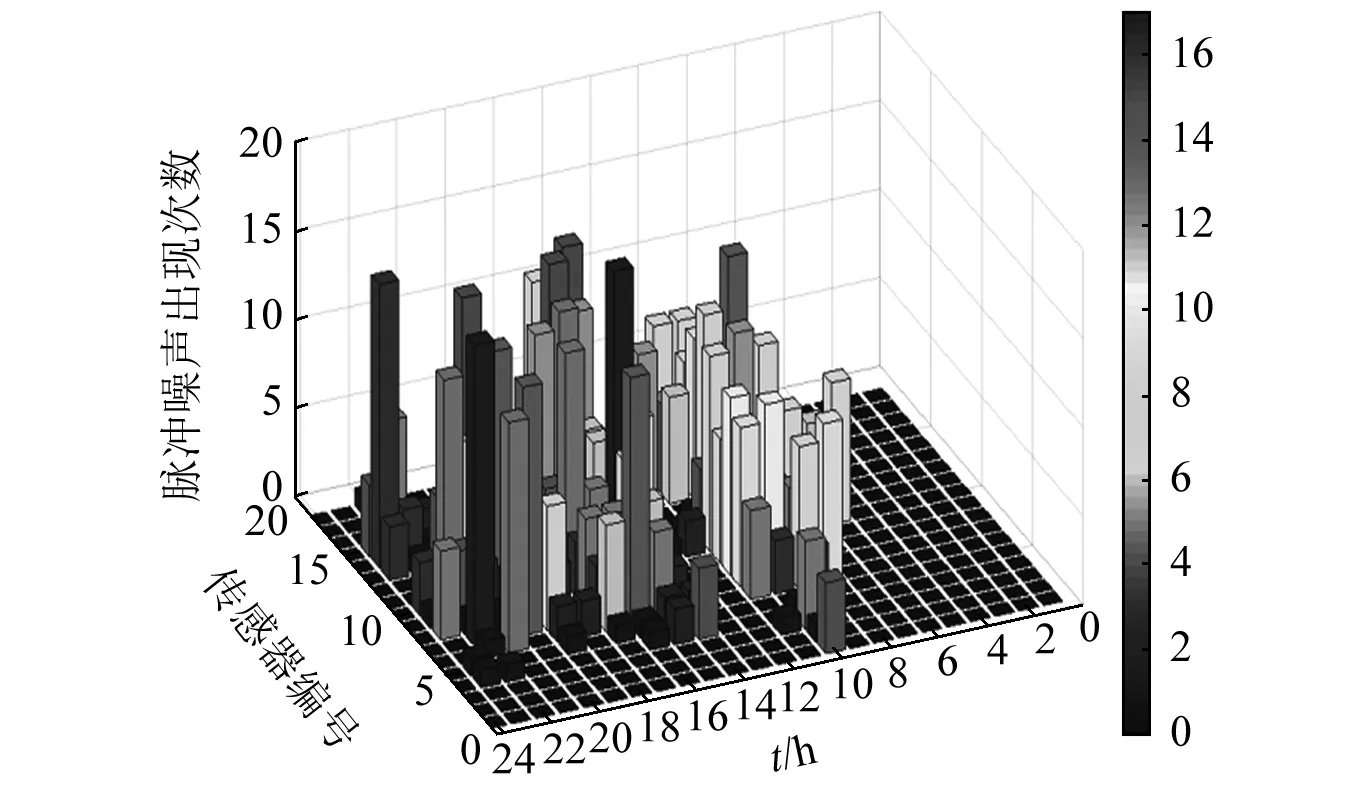
图13 一天内各个加速度传感器脉冲噪声出现次数Fig.13 Impulse noise for each acceleration sensor in a day

3.2 现场数据降噪结果

将本文建立的降噪算法应用于某一受到脉冲噪声影响的现场实测数据(见图14)，以验证该方法的有效性和合理性。将该数据进行峰度检验后确定受到脉冲噪声干扰的三个时间段分别是100～115 s，120～135 s和180～195 s。随后对数据进行小波包分解，并利用K-S检验非脉冲时段的小波包系数的分布，以(3,1)节点为例，图15～图16分别展示了该结点的小波包系数，以及非脉冲时段小波包系数的分布特点。

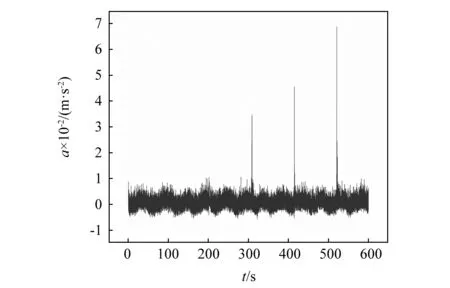
图14 受到脉冲噪声影响的现场实测加速度数据Fig.14 Acceleration data affected by impulse noise in the field monitoring

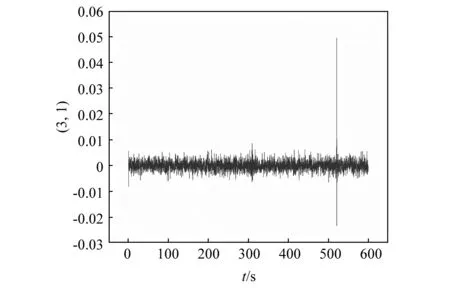
图15 现场数据(3,1)节点的小波包系数Fig.15 Wavelet packet coefficients of node (3,1) for field monitoring acceleration data

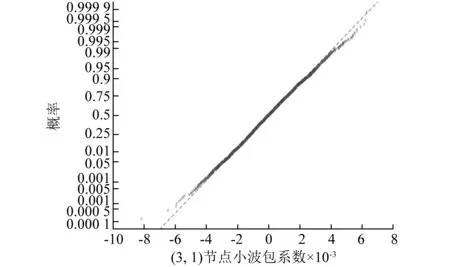
图16 现场数据(3,1)节点小波包系数正态分布概率图Fig.16 Probability plots of wavelet packet coefficients of node (3,1) for field monitoring acceleration data

如图16所示，非脉冲时段(3,1)节点的小波包系数较好的服从正态分布，其余节点的小波包系数和这一节点的分布特点具有一致性，这里就不再一一展示。根据上文的小波包系数阈值处理方法对脉冲时段的小波包系数进行加权处理，最后再对处理过后的小波包系数进行重构即可得到消除脉冲噪声后的加速度时程信号，降噪结果如图17所示。从图中可以看出，基于峰度检验和小波包分解的脉冲噪声处理方法很好的消除了现场信号中的脉冲噪声。

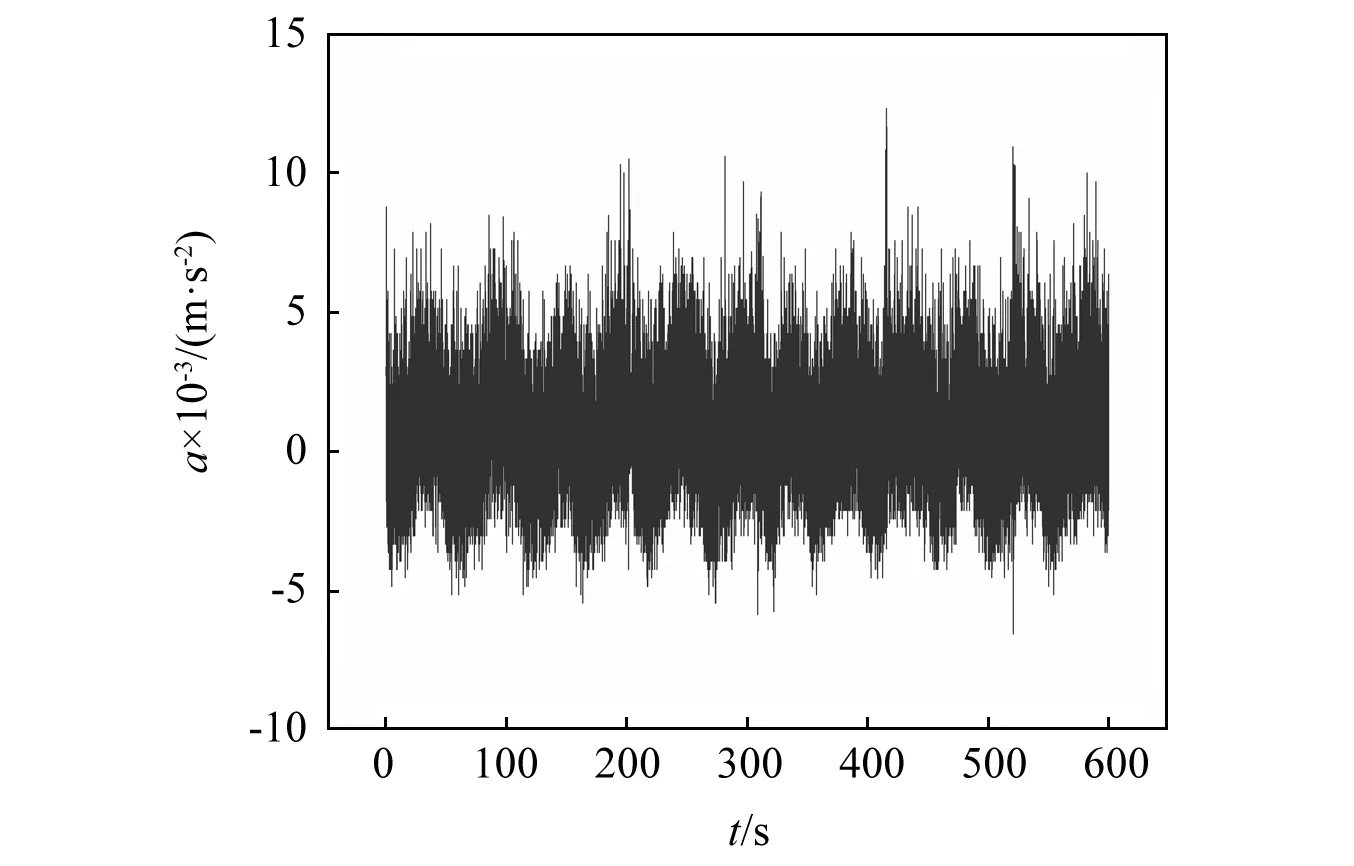
图17 降噪完成后的现场加速度数据Fig.17 Field measured acceleration data after noise reduction

4 结 论

本文针对随机海洋环境下某导管架平台监测数据经常出现的脉冲噪声开展了相关的降噪研究工作，考虑由于脉冲噪声通常具有较宽的频带，单一的频域或者时域处理方法具有一定的局限性，因此发展了一套基于峰度检验和小波包分解相结合的处理方法，经过数值模拟和现场数据的验证，利用该方法对含有脉冲噪声的数据处理后，信噪比有较大的提升，并且信号的相关性高，能有效消除脉冲噪声。

本文所开展的工作主要针对信号中的脉冲噪声，由于现场采集得到的信号是高度复杂的非线性耦合，其组成十分复杂，如何在脉冲噪声处理后，进行其余噪声的识别和降噪工作是下一步研究的重点，相关研究工作正在陆续开展。