一种球形机器人高速直线运动的自适应控制方法

马 龙，孙汉旭，宋荆洲，兰晓娟

(北京邮电大学 自动化学院，北京 100876)

球形机器人是一种基于内部驱动机构产生的偏心力矩与惯性力进行运动的新型移动机器人，能够实现防倾覆且全向稳定快速移动，具有运动效率高、能耗低的优势，在危险环境探测、狭窄空间作业、监控侦察等领域有着广泛应用前景[1]。球形机器人系统具有强耦合、欠驱动、非完整约束、非线性的特点，常规运动控制方法无法对其进行有效控制，同时运动过程中存在动力学模型构建不完整以及周围环境对运动产生未知干扰等不可测且不稳定的因素[2]。随着运动速度逐渐增大，上述不稳定因素给球形机器人运动控制带来的影响迅速增加，运动精度大幅下降，导致球形机器人无法应对如军事侦察爆破、通信网络中继等需要具备高速运动能力的任务。因此，开展面向球形机器人高速高精度运动的控制方法研究有重要意义。

近年来，国内外专家学者关注的球形机器人驱动机制主要分为以下三种：基于全向轮的偏心力矩驱动机制、基于摩擦的内驱动机制以及基于重摆的偏心力矩驱动机制，且相关研究主要集中在低速(对于20 kg左右的小型机器人，高速界定标准是2.5 m/s[3-4])运动状态下的控制策略方面，对高速运动状态下球形机器人控制策略的研究成果几乎未见。与另外两种驱动机制相比，基于重摆式偏心力矩驱动机制是一种具有较高可操作性和易于实现的驱动机制，但是运动过程中球壳与重摆运动的强耦合与欠驱动是导致其控制难度高的原因，然而其在运动速度方面有明显优势。因此以基于重摆的偏心力矩驱动机制进行驱动的球形机器人为研究对象，针对球形机器人典型运动形式——直线运动，本文开展高速运动状态下球形机器人直线运动的自适应控制研究。

针对基于重摆的偏心力矩驱动机制进行驱动的球形机器人直线运动控制，国内外学者开展了广泛的研究。Liu等[5]针对球形机器人的直线运动，提出了基于线性二次型调节器(linear quadratic regulator,LQR)的速度和角度控制器，但直线运动模型的线性化使该控制方法的准确性难以保证。赵勃等[6]通过在控制器中引入非线性摩擦模型进行反馈控制。Madhushani等[7]利用PID(proportional integral derivative)反馈正则化方法对基于重摆式偏心力矩驱动机制的环形机器人进行运动控制，该方法保证了对恒定扰动的鲁棒性。上述三种典型的研究成果对外界不可测的时变扰动不具备鲁棒性和自适应性。近年来，对基于重摆的偏心力矩驱动机制进行驱动的球形机器人直线运动控制的研究主要围绕滑模控制展开。滑模控制(sliding mode control,SMC)能够克服系统的不确定性,对未建模的干扰具有很强的鲁棒性，尤其是对非线性系统的控制具有良好的控制效果[8-9]。Yu等[10]提出一种对球形机器人直线运动进行解耦滑模控制的方法，通过设计系统的分层滑动面，使系统控制由多目标转换为单目标，大大降低控制器设计难度。Yu等[11]针对球形机器人直线运动问题提出一种模糊滑模控制(fuzzy sliding mode control,FSMC)方法，通过将第二层滑动面作为模糊逻辑系统的输入，通过运用模糊推理来得到滑模控制量。Yue等[12]运用自适应分层滑模控制(adaptive hierarchical sliding mode control,AHSMC)进行球形机器人直线运动速度的控制，通过与滚动摩阻的实时估算，使控制效果较为理想，但是超调量较大。另一种非常流行的对球形机器人直线运动控制的鲁棒控制方法是基于分数阶微积分的控制技术。分数阶微积分是普通导数和积分的任意阶数，能够提高球形机器人直线运动过程中稳态误差、收敛速度和轨迹跟踪性能[13]。周挺等[14]提出了基于分数阶微积分的分层滑模控制(fractional hierarchical sliding mode control,F-HSMC)方法，使系统在受到干扰的情况下具备更强鲁棒性，同时避免系统的超调量过大，但是同样未考虑控制方法的自适应性，且只给出了仿真结果。

从球形机器人直线运动控制方法的研究现状来看，大部分研究都采用了球形机器人直线运动的理想化或者经过线性化处理的动力学模型，以及适用于欠驱动系统的分层滑模控制器(hierarchical sliding mode controller,HSMC)，即使融入模糊或者自适应控制方法来应对无法通过传感器或数学模型描述的不确定因素，依然面临超调量过大、有限时间收敛性差以及抖振严重等情况，但由于球形机器人运动速度较低，所以对直线运动精度影响不明显。面对高速运动状态下的球形机器人，实际运动环境中的大量不确定因素以及控制算法在低速运动状态下的缺陷对球形机器人精准稳定运动产生的影响会迅速放大，导致上述控制器很难实现预期的运动精度。

HSMC能够对两个不同输出量同时实现控制，并且鲁棒性强、克服外界干扰以及参数摄动能力强。基于上述优势，针对高速运动状态下球形机器人控制方法对响应与收敛速度、抖振与超调量控制方面的要求，通过引入前馈补偿、积分项、分数阶微积分以及自适应律，本文提出了一种分数阶自适应分层积分滑模控制器(fractional adaptive hierarchical integral sliding mode controller,F-AIHSMC)，以获得高系统响应与收敛速度、强鲁棒性、对抖振能够有效抑制的高精度运动控制，实现高速运动状态下球形机器人精准稳定直线运动。

1 球形机器人直线运动的标准动力学模型

基于重摆式偏心力矩驱动机制的球形机器人示意图如图1所示。通过主框架上垂直安装的长轴电机和短轴电机共同驱动，球形机器人能实现全方位运动。当球形机器人长轴电机或短轴电机单独驱动时，球形机器人能沿着X轴方向或Y轴方向分别进行直线运动。

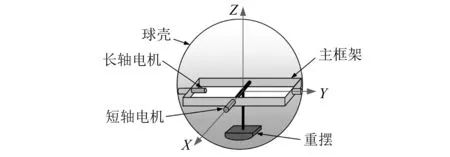
图1 基于重摆式偏心力矩驱动机制的球形机器人示意图Fig.1 The spherical robot driven by the eccentric torque driving mechanism based on weight pendulum

以沿X轴方向直线运动作为研究对象，球形机器人直线运动简化模型如图2所示，球形机器人在长轴电机理论输出力矩τ的作用下在XOZ平面内沿X轴滚动。其中：球壳质量和转动惯量分别为m1和I1；主框架质量和转动惯量分别为m2和I2；重摆质量和转动惯量分别为m3和I3；球壳半径为R；重摆摆长为L；球壳相对初始位置滚过角度为θ；球心沿X轴方向的位移为x，且x=θR；重摆相对垂直方向摆起角度为φ；球形机器人总质量为M，且M=m1+m2+m3。

图2 球形机器人直线运动的简化模型Fig.2 Simplified model of linear motion of the spherical robot

基于拉格朗日法建立球形移动机器人直线运动的理想动力学模型为[15]

(1)

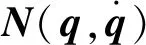
由式(1)所示的动力学模型，能够得到球形机器人在直线运动时受到的非完整约束为

(2)

其中，

h2(φ)=m3RLcosφ-(m3L2+I2+I3)

针对球形机器人的大部分研究都基于如上所示的理想状况下动力学模型展开。在实际应用中，球形机器人机构存在多种复杂摩擦问题以及外界扰动，摩擦与扰动产生的多项未知量使球形机器人的动力学模型复杂化，尤其是在高速运动状态下，摩擦与扰动问题无法忽略。针对高速运动状态下的球形机器人，本文建立了如式(3)所示的球形机器人标准动力学模型。

(3)

式中：τm为电机的输出力矩；τf为运动过程中受到的摩擦项；τd为运动过程中受到的外界扰动。

根据扰动是否可控，将τd分为可控扰动τdv与不可控扰动τdu。同样的，将τf分成线性τfx与非线性τfn两部分。因此，标准动力学模型可写为

(4)

高速运动状态下可控扰动主要来自运动过程中地面对球壳的滚动摩阻力偶矩，其能够严重影响球形机器人的精准运动。根据“滚动摩阻力偶矩定律”，球形机器人在滚动过程中受到的滚动摩阻力偶矩为[16]

(5)

式中：δ为滚动摩阻系数；FN为球形机器人对支撑面产生的正压力，表达式如(6)所示。

(6)

高速运动状态使球形机器人受到的摩擦更复杂。球形机器人高速直线运动过程中，重摆相对于球壳发生相对转动，轴承的黏性阻尼导致转动关节中产生的摩擦力矩是线性摩擦的主要来源，其大小与关节转动速度成正比，方向与关节转动方向相反，表达式为

(7)

式中，ς为黏性摩擦因数。

令可控补偿力矩表达式为

(8)

其中，

将不可控扰动τdu、非线性摩擦τfn等不确定因素用τi表示，则球形机器人的标准动力学模型可写为

(9)

根据式(9)可知，在设计面向高速运动的球形机器人控制器时，需要综合考虑以下3点重要因素：①与球形机器人自身相关参数；②高速运动过程中的可控因素；③高速运动过程中的不确定性因素。

用ξ(t,u(t))表示包含不可控的有界未知扰动以及非线性摩擦等不确定因素的不确定项。将直线运动的标准动力学模型转换为式(10)所示的等式，进一步表示为式(11)所示两个子系统的状态空间表达式。

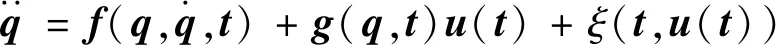
(10)

(11)

其中，

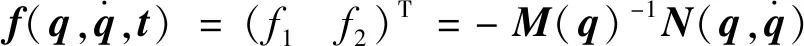
由于滚动过程中球形机器人受到滚动摩阻力偶矩的影响，滚动过程中的球形机器人处于动态平衡状态时，重摆摆起平衡角的动态变化是设计系统控制器时不容忽视的问题，否则无法对球形机器人实现精准控制。根据文献[17]中对重摆摆起平衡角的描述，平衡状态下的摆起平衡角可用式(12)进行确定。

(12)

本文提出的控制方法目的是设计合理的电机输出扭矩控制律，使高速运动状态下的球形机器人运动轨迹x(t)和重摆的摆动位置φ(t)均能收敛到各自的期望值xd(t)和φd(t)，运动轨迹误差ex(t)=xd(t)-x(t)与重摆摆动位置误差eφ(t)=φd(t)-φ(t)尽可能小，以实现高速运动状态下球形机器人精准直线运动。

2 分数阶自适应分层积分滑模控制器

面对高速直线运动球形机器人的精准控制问题，基于式(10)所示的状态空间表达式，通过引入前馈控制的思想，在理想状态下的力矩τ作用于球形机器人系统的同时，将具有近似精确模型的影响因素τfc提前对高速运动控制系统进行补偿，能够降低系统迟滞给高速运动精准性带来的影响，使球形机器人运动误差降低，同时改善系统的动态特性。

2.1 第一层滑模面的构建

与SMC相比，积分滑模控制(integral sliding mode control,ISMC)通过引入积分项，以提高控制系统响应速度与鲁棒性。针对球形机器人这种欠驱动系统控制问题中常用的HSMC方法，本文通过将ISMC与其进行融合，并且基于球形机器人的标准动力学模型，建立分层积分滑模控制器(integral hierarchical sliding mode controller,IHSMC)。

由于HSMC的总控制律需要将由第一层滑模面得出的滑动控制律包含在内，同时需要包含第二层滑模面的趋近控制律，以保证控制系统的渐进稳定以及第二层滑模面可达。因此，IHSMC的控制律如式(13)所示

u(t)=ue(t)+usw(t)

(13)

式中：ue(t)为滑动控制律，能够通过系统的第一层滑模面求得；usw(t)为趋近控制律。

球形机器人两个子系统的动力学方程均为二阶非线性函数，因此本文将积分算子融入第一层滑模面中。考虑到积分项能够加快系统响应，同时也能够使系统响应的超调量增加，因此需要加入微分项来降低系统超调量。分别设计针对球壳位移和重摆摆角的第一层滑模面S1(t)和S2(t)，如式(14)所示[18]。

(14)

式中：k1>0；k2>0。

为了使球形机器人直线运动控制器具有高系统响应速度、有限时间快速收敛以及精确控制性能，将Riemann-Liouville分数阶微积分融入IHSMC控制器第一层滑模面中，设计了F-AIHSMC的第一层滑模面[19]

(15)

令控制目标期望值qd=(xdφd)T。对式(15)求关于时间的二阶微分，结合式(11)可得[19]

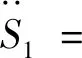
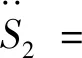
(16)

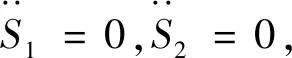
f1-ξ1]

f2-ξ2]

(17)

子系统中的不确定项ξ1和ξ2本质为具有物理边界的未知函数。根据式(11)可知，不可控扰动能够分别作用于两个子系统，导致第一层滑模面中产生误差。为了对第一层滑模面中的误差进行有效约束，需要在子系统控制律中融合对不可控扰动的自适应反馈控制来抵消其影响，进而增强系统鲁棒性。根据积分滑模控制原理，式(17)所示的每个子系统控制律uei只能使子系统到达第一层滑模面上。将稳定控制律uei-s作为反馈控制部分加入子系统控制律中，能够从子系统层面提高球形机器人系统对外界扰动以及系统抖振现象的鲁棒性。子系统控制律uei可更新为

f1-ξ1]+ue1-s(t)

f2-ξ2]+ue2-s(t)

(18)

本文选取如式(19)所示的稳定控制律表达式。

(19)

式中，μi和ηi为稳定增益参数。

基于式(18)与式(19)，可得子系统控制律为

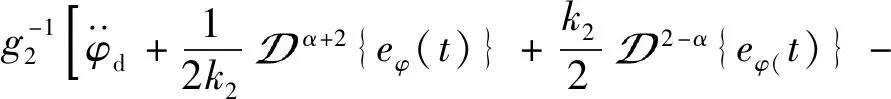
(20)

理想情况下，当式(20)所示的稳定增益大于未知影响因素的上界时，控制器具有很强的鲁棒性。但是实际应用时，只能通过将稳定增益参数设置到非常大来应对未知影响因素上界不明确的情况[20]。由于实际应用中稳定阶段控制器具有不可避免的缺陷以及控制过程中存在延时，上述处理方法能够导致控制系统发生异常震荡，对球形机器人系统产生很大危害。面对分层滑模控制，子系统在控制过程中的缺陷最终会在系统总控制律部分发生叠加与耦合，如果在第二层滑模面再对其进行处理，会增大处理难度，最终导致球形机器人系统控制误差加大。因此，针对子系统稳定控制律uei-s(t)的稳定增益参数μi和ηi，本文提出对其一阶导进行自适应估计

(21)

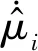
因此，F-AIHSMC的自适应子系统控制律分别为

(22)

2.2 第二层滑模面的构建

构建第二层滑模面S(t)

(23)

式中：c1>0；c2>0。

基于式(22)所示的自适应子系统控制律，将式(23)对时间求一阶微分，得到

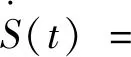
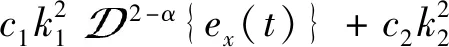
(24)

为使第二层滑动变量S(t)快速收敛于零，本文使用如式(25)所示的指数趋近律设计F-AIHSMC。

(25)

式中，ε1，ε2均为大于0的常数。根据式(24)与式(25)，能够求得趋近控制律usw(t)为

(26)

将其代入式(13)，可求得F-AIHSMC的控制律为

u(t)=ue1(t)+ue2(t)+usw(t)=

(27)

F-AIHSMC的结构示意图如图3所示。针对F-AIHSMC，我们能够得出以下定理：

图3 F-AIHSMC结构示意图Fig.3 The structure of the F-AIHSMC

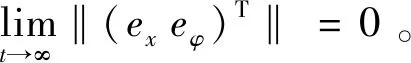
证明选取Lyapunov函数

根据式(21)可得V关于时间的一阶导为

(28)

将式(27)代入式(28)得V关于时间的一阶微分为

-ε1·S2-ε2|S|

(29)

因此，第二层滑模面S是渐进稳定的，在F-AIHSMC中，第一层滑模面同样需要渐进稳定。

定理2假设球形机器人直线运动的期望运动轨迹在[0 +∞)内是连续的且有界的函数。对于具有式(9)所示动力学方程的球形机器人系统，在控制律式(27)的作用下，第一层滑模面S1与S2是渐近稳定的。

证明对式(29)进行积分，能够得到

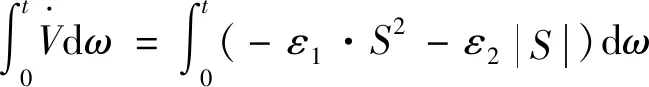
(30)

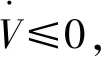
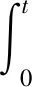
(31)

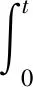
由式(29)可得，滑模面S是否稳定与ε1和ε2无关。因此假设如式(32)所示的两个不同的滑模面SA与SB，参数cA1，cB1与c2均为正实数。

(32)

令SA(t)>SB(t)，可得

(33)

因此，S1渐进稳定。运用同样的证明方法可得S2渐近稳定。定理2证明结束。

针对式(27)中提出的控制律，如果稳定增益参数增大，符号函数(sign)能够导致系统抖振增大。因此，为了避免该情况发生，将F-AIHSMC控制律修改为

u(t)=ue1(t)+ue2(t)+usw(t)=

(34)

F-AIHSMC的自适应子系统控制律修改为

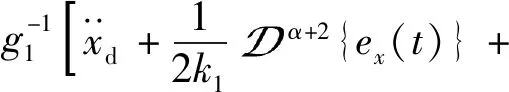
(35)

其中，

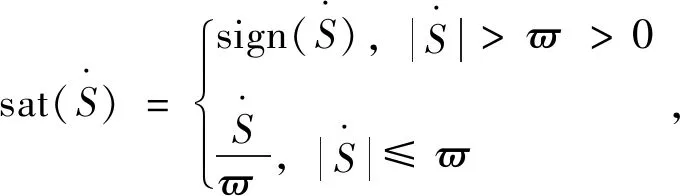
3 实验研究

为了验证F-AIHSMC对高速直线运动状态下球形机器人精准控制的有效性，以BYQ-GS型球形机器人为实验平台，运用F-AIHSMC进行高速直线运动控制实验，并且运用传统的HSMC与Yue等研究中提出的AHSMC进行相同的高速直线运动控制作为对比实验。

3.1 实验对象

BYQ-GS球形机器人的三维模型与实物如图4所示，性能参数如表1所示。与传统球形机器人相比，BYQ-GS球形机器人面向高速运动任务需求，基于轻量化设计原则，将玻璃纤维增强聚合物材质球壳与基于3D打印的光敏树脂材质框架相结合，内部结构经过拓扑优化设计，将重摆与电源系统进行功能性融合，在总体质量大幅降低的前提下，能够保证重摆质量相对总体质量的高占比，因此可以使球形机器人实现高速灵活运动。通过采用带有绝对编码器的直流无刷电机、Xsens MTi-300惯性航姿测量系统、Trimble BD992-INS多星多频高精度定位测向板卡相结合的方式，BYQ-GS球形机器人能够实现对运动过程的控制与测量。

1.重摆；2.主框架；3.惯性航姿测量系统；4.长轴电机；5.短轴电机；6.主控制板；7.高精度定位测向板卡。图4 BYQ-GS型高速运动球形机器人的三维模型与实物图Fig.4 The 3D model and physical prototype of the BYQ-GS spherical robot

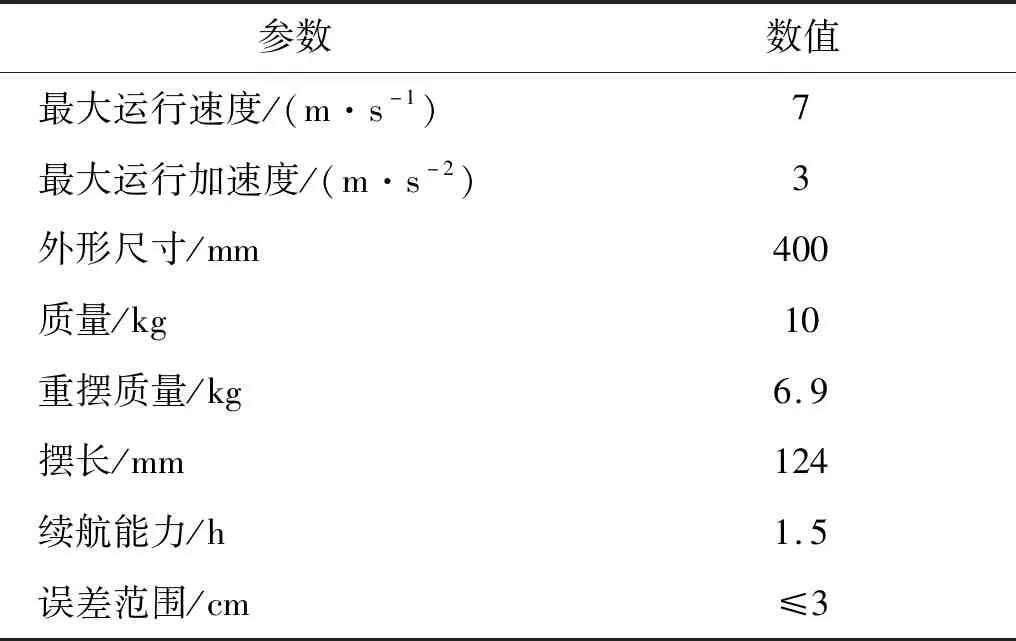
表1 BYQ-GS型高速运动球形机器人性能参数Tab.1 Performance parameters of BYQ-GS spherical robot

实验场地示意图如图5所示。实验场地45 m处设置15°双向短坡道，47 m处设置2 m长、30 mm厚海绵轨道，52 m处设置15°单向短坡道，以对实际工况中由于多种路面状况引起的复杂扰动进行模拟。

图5 实验场地示意图Fig.5 Schematic diagram of experimental field

3.2 F-AIHSMC最优参数确定

为了确定F-AIHSMC的最优参数，本文基于BYQ-GS球形机器人对F-AIHSMC开展仿真研究。在不考虑分数阶微积分的情况下，即式(15)中的α为1，使用软件Matlab中的全局优化工具箱(global optimization toolbox)通过模式搜索对控制参数(k1,k2,c1,c2,ε1,ε2)以及自适应律参数(ρ1,ρ2,κ1,κ2)最优值进行确定，可得对F-AIHSMC收敛速度以及控制性能最优的参数选择为

(k1,k2,c1,c2,ε1,ε2)=(0.697,2.187,5.896,3.434,10.103,0.117)
(ρ1,ρ2,κ1,κ2)=(17.3,21.8,12.2,14.9)

基于上述最优值，使用软件Matlab中的分数阶建模和控制工具箱(FOMCON)，通过试差法对分数阶微积分的α参数进行调整，可得分数阶微积分的α参数的最优值为α=0.65。

对分数阶微积分进行离散化是分数阶在实验中的主要实现方法。本文运用了文献[22]中提出的Al-Alaoui+CFE离散化方法，在计算过程中将分数阶算子离散化为式(36)所示的近似形式。

(36)

式中：T为采样周期；CFE{u}为连分式展开；Pp(·)和Qq(·)为变量s-1的互质多项式，通常设定Pp(·)的阶次P与Qq(·)的阶次Q均等于迭代次数n。

迭代次数越多，计算越复杂。在实验中，我们选取迭代次数n=3。参考徐智超研究中表3-2，当n=3时，选取如式(37)所示的表达式。

Pp(s-1)=(-288α2+27)s-3+(-64α3-284α)s-3+

(672α2+1 827)s-2+2 520αs-2-

2 940αs-1-6 615s-1+5 145

Qq(s-1)=(-288α2+27)s-3-(-64α3-284α)s-3+

(672α2+1 827)s-2-2 520αs-2+

2 940αs-1-6 615s-1+5 145

(37)

3.3 实验过程和结果

针对不同的期望状态，本文设置了3组实验，在每组实验中，分别将三种不同的控制方法作用于BYQ-GS球形机器人的高速直线运动，作为每组实验的3个子实验。为了保证实验数据的可靠，同时更直观的对实验结果进行对比，在子实验过程中，我们都重复进行10次并取其数据的平均值，再运用Savizkg-Golag平滑算法(30点2次)对数据进行预处理，作为该次子实验的最终实验数据。基于所得实验数据，我们对本文提出的F-AIHSMC、Yue等中提出的AHSMC以及传统的HSMC的控制效果进行对比。本文将每组实验中BYQ-GS球形机器人初次收敛到期望状态的控制过程定义为初始控制阶段，受到扰动后收敛到期望状态的控制过程定义为扰动控制阶段。

本文运用了收敛时间tr、运动位置误差的最大绝对值emax以及位置误差的均方根误差(RMSE)值三项指标，对BYQ-GS球形机器人在三种控制器下的直线运动控制效果进行清晰的展示。实验场景如图6所示。

1.扰动模拟区域；2.初始状态；3.BYQ-GS通过双向短坡道；4.BYQ-GS通过海绵轨道；5.BYQ-GS通过单向短坡道。图6 实验场景图Fig.6 The experimental scene

实验1球形机器人初始状态为(x0,φ0)=(0,0)，设期望状态为(xd,φd)=(3t,τr/m3gL)。图7为球形机器人运动轨迹误差ex(t)=xd(t)-x(t)、重摆的摆动位置误差eφ(t)=φd(t)-φ(t)与球形机器人速度变化图。

图7 实验1的子实验相关数据变化对比图Fig.7 Comparison of relevant data variation of sub-experiment of experiment 1

定义实验1的初始控制阶段为0～10 s，扰动控制阶段为10～20 s。BYQ-GS球形机器人在三种控制器下的直线运动控制效果如表2所示。

表2 实验1中球形机器人在三种控制器作用下直线运动效果Tab.2 Motion control effect of spherical robot under three controllers in experiment 1

实验2球形机器人初始状态为(x0,φ0)=(0,0)，设期望状态为(xd,φd)=(3.5t,τr/m3gL)。图8为球形机器人运动轨迹误差ex(t)=xd(t)-x(t)、重摆的摆动位置误差eφ(t)=φd(t)-φ(t)与球形机器人速度变化图。

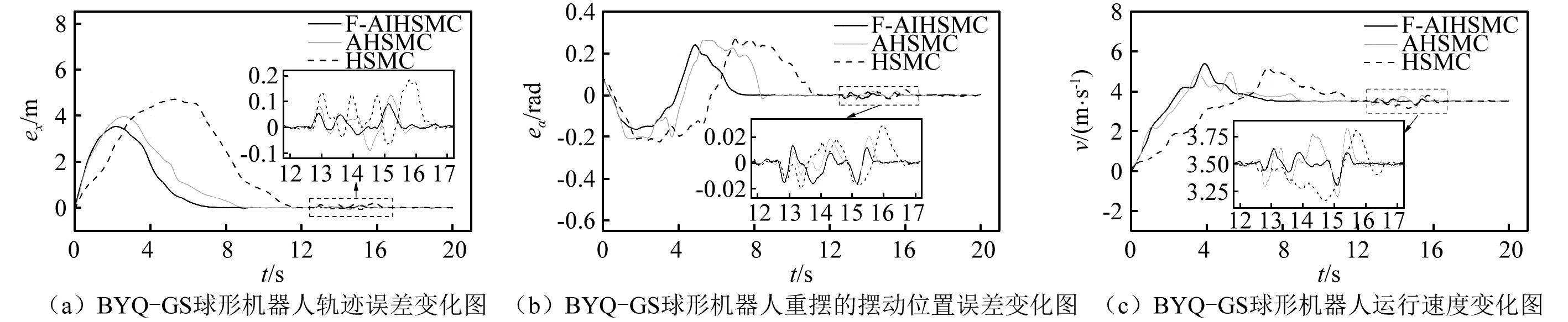
图8 实验2的子实验相关数据变化对比图Fig.8 Comparison of relevant data variation of sub-experiment of experiment 2

定义实验2的初始控制阶段为0～12 s，扰动控制阶段为12～20 s。在三种控制器作用下的BYQ-GS球形机器人直线运动控制效果如表3所示。

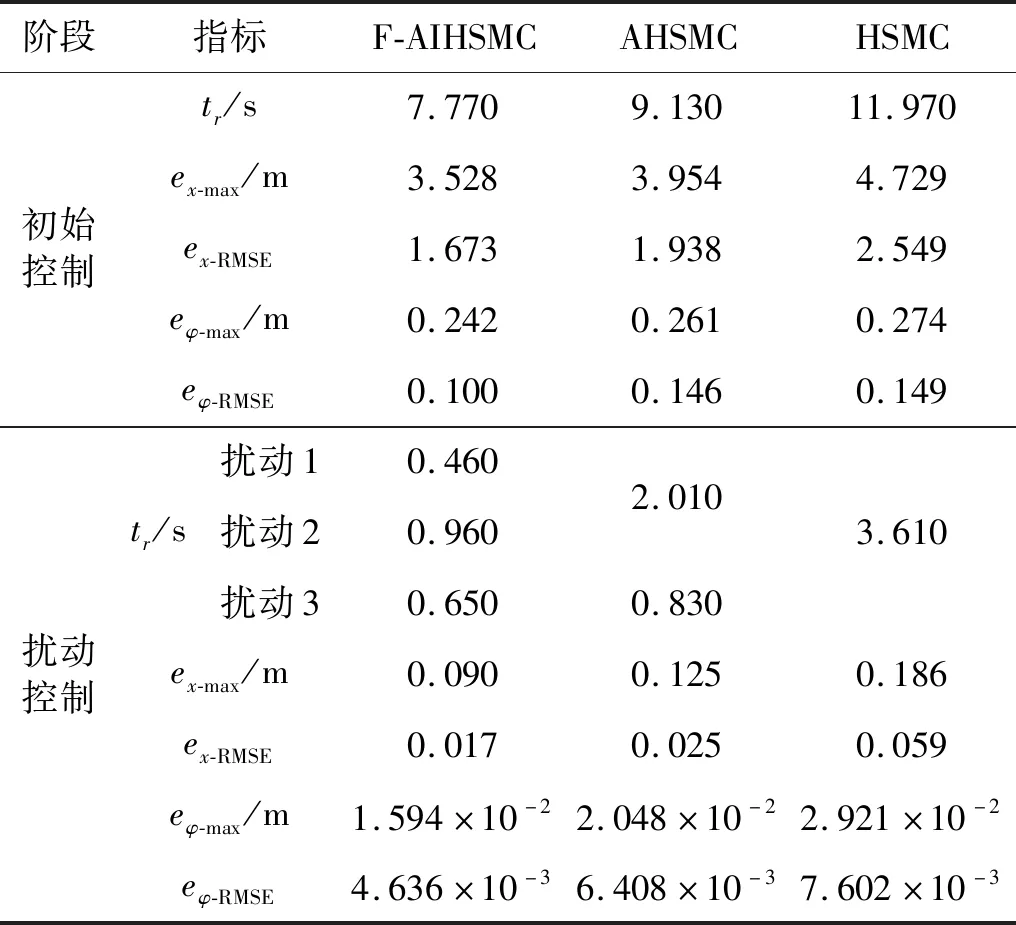
表3 实验2中球形机器人在三种控制器作用下直线运动效果Tab.3 Motion control effect of spherical robot under three controllers in experiment 2

实验3球形机器人初始状态为(x0,φ0)=(0,0)，设期望状态为(xd,φd)=(4t,τr/m3gL)。图9为球形机器人运动轨迹误差ex(t)=xd(t)-x(t)、重摆的摆动位置误差eφ(t)=φd(t)-φ(t)与球形机器人速度变化图。

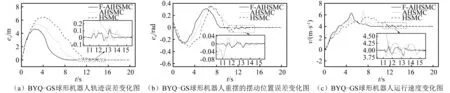
图9 实验3的子实验相关数据变化对比图Fig.9 Comparison of relevant data variation of sub-experiment of experiment 3

实验3中运用HSMC进行球形机器人直线运动控制时，在遇到扰动1前BYQ-GS球形机器人未能初次收敛到期望状态，因此以到达扰动1的期望时间为两个阶段分界点，即定义实验3初始控制阶段为0～11.25 s，扰动控制阶段为11.25～20 s。球形机器人在三种控制器下的直线运动控制效果如表4所示。

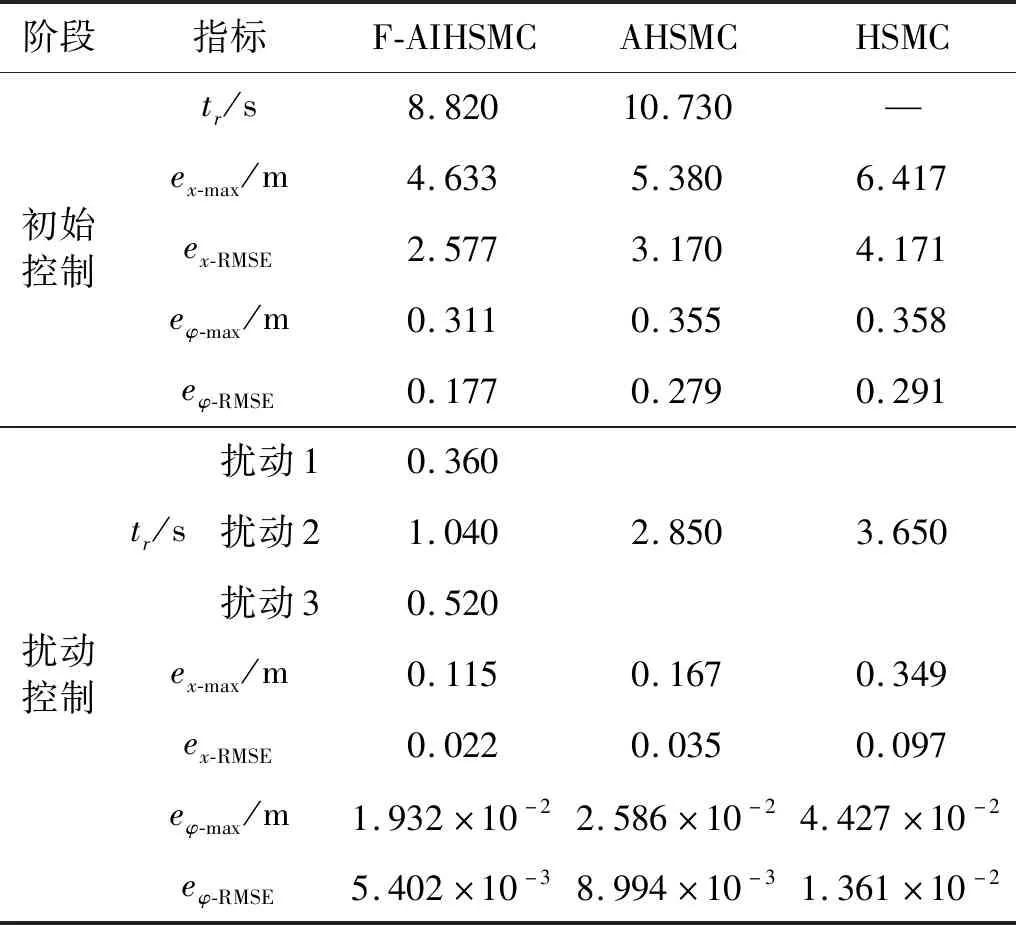
表4 实验3中球形机器人在三种控制器作用下直线运动效果Tab.4 Motion control effect of spherical robot under three controllers in experiment 3

3.4 实验结果分析

基于上述实验数据，运用综合定量评价法对F-AIHSMC与AHSMC、F-AIHSMC与HSMC在两个控制阶段的综合控制效果分别展开对比。实验指标分为三种类型：tr，emax，eRMSE，总共涉及到五个指标：tr，ex-max，ex-RMSE，eφ-max，eφ-RMSE，因此综合定量评价公式为

(38)

其中：c为指标的权重系数，每个指标权重系数均为c=0.2；(vi)a为指定控制器(AHSMC或HSMC)第i个指标值；(vi)b为F-AIHSMC第i个指标值。

由于初始控制阶段部分控制方法未收敛，此时

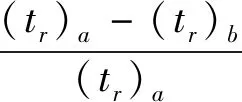
在扰动控制阶段，由于存在三个扰动，因此扰动控制阶段的tr又可划分为tr-1，tr-2，tr-3，此时

同理，在扰动控制阶段，部分控制方法在面对第i个扰动时未收敛，此时

根据式(38)可得F-AIHSMC与AHSMC、F-AIHSMC与HSMC在两个控制阶段控制效果的综合对比。对比结果如表5所示。

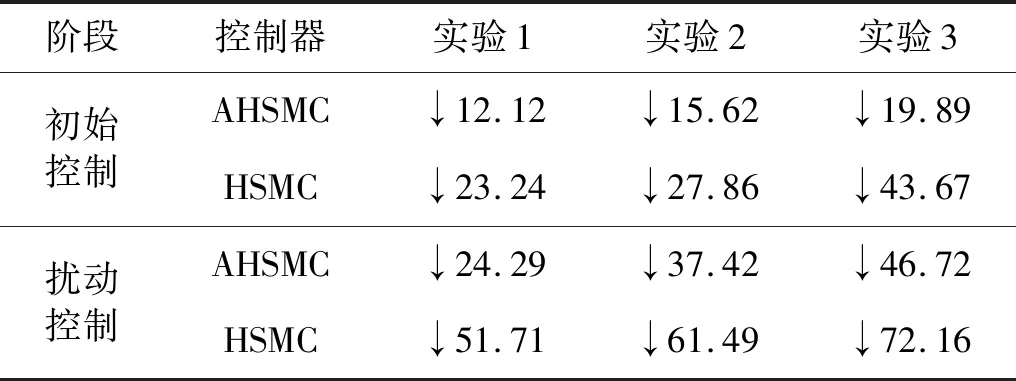
表5 F-AIHSMC与其余两种控制方法的控制效果对比结果Tab.5 Comprehensive comparison of F-AIHSMC and the other two control methods %

根据三组实验数据以及综合控制效果对比结果，F-AIHSMC的tr,emax以及eRMSE三项指标均为最优。在三组实验的初始控制阶段，F-AIHSMC与AHSMC均能收敛，但运行速度的期望值为4 m/s时，HSMC未能实现收敛。在三组实验的扰动控制阶段，当BYQ-GS球形机器人面对3个固定位置的扰动时，F-AIHSMC均能实现迅速收敛；在第二组与第三组实验中，即期望运行速度达到3.5 m/s以上时，AHSMC无法实现对3个扰动的同时收敛；HSMC在三组实验中均无法实现对3个扰动的同时收敛。通过对三组实验的tr进行对比可以得出，与AHSMC以及HSMC相比，F-AIHSMC在加快系统响应速度和收敛速度方面具有明显优势。通过对三组实验的ex-max与eφ-max进行对比可以得出，与AHSMC以及HSMC相比，F-AIHSMC在减小系统超调量方面具有明显优势；通过对三组实验的ex-RMSE与eφ-RMSE进行对比，结合三组实验中基于不同控制方法的球形机器人运行速度变化趋势可以得出，与AHSMC以及HSMC相比，F-AIHSMC在增强系统稳定性方面具有明显优势；通过对三组实验的扰动控制阶段收敛情况进行对比可以得出，在面对未知扰动时，与AHSMC以及HSMC相比，F-AIHSMC能够使系统具有更强的鲁棒性。因此，与AHSMC以及HSMC相比，F-AIHSMC的控制效果最好，且随着期望运行速度从3 m/s提升至4 m/s，F-AIHSMC的控制优势越来越明显。

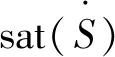
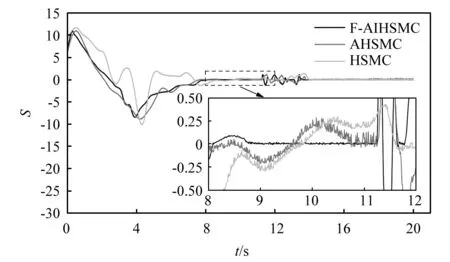
图10 三种控制方法的总滑模面变化对比图Fig.10 Comparison of the total sliding surface change of the three control methods

4 结 论

本文以球形机器人高速直线运动问题作为研究对象，通过理论与实验相结合的方式，开展面向球形机器人高速直线运动自适应控制方法的研究：通过建立适用于高速直线运动状态下的标准动力学模型，并且基于该模型，将前馈控制、积分项与分数阶微积分以及自适应控制融入传统的分层滑模控制方法中，提出了一种分数阶自适应分层积分滑模控制器F-AIHSMC，并且基于BYQ-GS球形机器人对F-AIHSMC进行了直线运动控制实验。结果表明，在球形机器人高速运动状态下，与传统的HSMC以及具有自适应功能的AHSMC相比，该方法实现了高系统响应速度与收敛速度，并且具有更好的稳定性和鲁棒性。

系统的不确定性以及外部环境的未知扰动能够对球形机器人的精准运动产生影响，并且与低速运动状态相比，该影响在高速运动状态下会成倍增加，这是导致球形机器人在高速运动状态下运动精度降低的重要原因。通过对球形机器人高速直线运动控制方法的研究，使球形机器人实现了高速精准的直线运动，为开展球形机器人高速精准的全方位控制研究打下了坚实的基础，该研究对球形机器人的应用推广方面有重要的指导意义和促进作用。