桥梁动态称重迭代算法的理论与试验研究

张龙威，汪建群，陈 宁，孙洪鑫

(湖南科技大学 土木工程学院，湖南 湘潭 411100)

随着国民经济的高速发展，交通量迅速增长，公路桥梁中的超载现象变得越来越严重。超载车辆会造成桥梁不可恢复的损伤，并加速既有病害发展，危及结构安全，甚至造成桥梁坍塌。如何控制超载车辆，防止既有桥梁的状况加速恶化，已成为桥梁养护管理部门的棘手难题。

目前，监控超载车辆的方式主要有两种：路面称重系统和桥梁动态称重系统。其中，路面称重系统(weigh-in-motion，WIM)[1]通过在路面埋置传感器获取通行车辆的轴重。由于车轮作用于路面传感器上的响应时间较短，仅有几毫秒，传感器附近路面与车轮之间相互振动会影响称重的精度。当车速较快或路面不平整度较差时，WIM的称重精度较低。此外，路面传感器的安装与更换需要中断交通才能进行[2]。桥梁动态称重系统(bridge weigh-in-motion，BWIM)[3- 4]是通过安装在桥梁主梁底部的传感器采集车辆驶过桥梁产生的动力响应，反算车辆轴重。相比WIM系统，BWIM系统安装方便、测试隐蔽，无需中断交通，用于称重的响应时间较长(1～5 s左右)，称重精度高且稳定性好。BWIM系统在美国、日本以及欧洲等广泛应用[5]。

商用BWIM系统通常选用Moses算法作为核心构架进行桥梁的动态称重，如：都柏林大学和爱尔兰ROD-IS公司开发的DuWIM系统，斯洛文尼亚CESTEL和ZAG公司开发的SiWIM系统等[6]。Moses算法最早由Moses[7]提出，是以桥梁跨中位置的理论影响线为基础，建立轴重求解方程。由于桥梁实际的边界条件、材料特性等较难真实地模拟，理论影响线与真实影响线之间会存在一定的差异,从而降低称重精度。针对这一问题，OBrien等[8-9]提出用实测影响线代替理论影响线进行桥梁动态称重。实测影响线是从桥梁的车桥动力标定试验数据中提取得到，能够较真实地反映桥梁的力学特性。修正后的Moses算法具有更高的计算精度，但是Moses算法本身存在一定的局限性，即：轴重求解方程是病态方程，当路面较粗糙或车轴轴距较小时，轴重识别精度较低[10]。为此，Rowley和Gonzalez引入Tikonov正则化技术修正病态方程。这种方法虽然可以提高单轴轴重精度，但是，作为影响计算精度的正则化参数，它的选取需要人为干预，无法通过算法自动选定[11]。

为进一步提高BWIM系统的轴重识别精度，本文提出桥梁动态称重迭代算法，首先，基于Moses算法，将桥梁实测影响线作为基准影响线识别车辆轴重；然后，将计算得到的车轴轴重作为已知量，用影响线算法反算出桥梁影响线作为新的基准影响线；最后，反复使用Moses算法和影响线算法更新基准影响线和车辆轴重，直到相邻两次迭代得到的车辆轴重差值小于或等于阈值为止，所对应的车辆轴重即为桥梁动态称重迭代算法的计算值。以实桥的车桥动力试验作为实例，分别用基于实测影响线的Moses算法(后文简称：商用BWIM算法)和桥梁动态称重迭代算法识别车辆轴重，对比分析两种算法的识别精度，并得出相关结论。

1 桥梁动态称重理论研究

在商用BWIM系统中：首先，在选定的桥梁进行车辆动力试验，作为标定试验；然后，用影响线法从标定试验数据中提取出桥梁的实测影响线；最后，基于Moses算法，用实测影响线对行驶在桥面上的车辆进行轴重识别[12]。

1.1 Moses算法

Moses算法最早是由Moses提出。该算法以梁桥作为研究对象，假定桥梁为一维线弹性梁，根据桥梁跨中位置的理论弯矩影响线(I)计算出桥梁跨中的理论弯矩响应(MT)，基于最小二乘法原理，拟合出与实测弯矩响应最接近的理论弯矩响应，此时，弯矩响应拟合值所对应的车辆轴重即为桥梁动态称重的计算值。

在Moses算法中，理论弯矩响应(MT)可通过每个车轴乘以相应的影响线数值再叠加求和得到，其表达式为

(1)

式中：t为影响线和弯矩响应的时刻或车辆在桥上移动的位置；N为车辆的总轴数；Ai为车辆第i个车轴的轴重；Ii为第i个车轴所对应的桥梁影响线坐标值。

对桥梁荷载响应的实测弯矩响应(MM)和理论弯矩响应(MT)之间差值的平方和作最小化处理，建立误差函数E，如式(2)所示

(2)

式中，K为荷载响应的总时间。误差函数中，实测弯矩响应为已知量，理论弯矩响应可通过未知的车辆轴重和已知的理论弯矩影响线由式(1)计算得到。根据最小二乘法原理，误差函数对每个车轴轴重的偏导为零时，误差函数取最小值。通过求解计算，得出行驶在桥梁上的车辆轴重(详细过程，可参见Moses的研究)。车辆轴重的表达式为

{A}=([I]T[I])-1[I]T{MM}

(3)

式中，[I]为车辆所对应的桥梁影响线矩阵，维度为K(时间)×N(车轴)。

1.2 影响线算法

影响线算法由OBrien等提出，是指用车桥动力响应信号提取出的桥梁实测影响线代替理论影响线，再以Moses算法计算车辆轴重。相比理论影响线，桥梁实测影响线不仅取决于桥梁的实际刚度，还与桥梁的路面不平整度、车速及车桥耦合效应密切相关。由于桥梁实测影响线是直接从桥梁的车桥动力响应信号提取而来，它在一定程度上更能准确地反映桥梁实际的力学性能。

实测影响线的计算是基于最小二乘法原理，利用桥梁荷载响应测试值和理论值之间形成的误差函数(如式(2)所示)计算得到。与Moses算法不同，影响线算法的未知量是影响线，车辆轴重为已知量。为了获取误差函数的最小值，使荷载响应的理论值能够准确地预测响应的实测值，对式(2)中的影响线求偏导，并取值为零，如式(4)所示

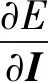
(4)

式中：I为影响线向量。求解式(4)，并整理结果，可得

{I}=([A]T[A])-1[A]T{MM}

(5)

式中，[A]为车辆轴重矩阵，是已知量。通过式(5)，计算得到桥梁的实测影响线。

1.3 BWIM迭代算法算法

在商用BWIM系统中：首先，对选定的桥梁进行车辆动力试验，作为标定试验；然后，用影响线法从标定试验数据中提取出桥梁的实测影响线；最后，基于Moses算法，用实测影响线对行驶在桥面上的车辆进行轴重识别。由于实桥标定试验现场条件的限制，通常用于标定影响线的车桥动力试验次数较少，得到的实测影响线存在欠拟合的情况，较难全面地模拟桥梁真实地受力特性。为解决这一问题，笔者所在研究团队提出桥梁动态称重迭代算法。桥梁动态称重迭代算法的具体计算流程如下所示：

步骤1选定一组车桥动力响应信号，用影响线算法计算出桥梁的实测影响线，作为车辆轴重识别的基准影响线Io；

步骤2基于Moses算法，用基准影响线Io对行驶在桥面上的车辆进行轴重识别。以实测的桥梁动力响应信号MM为例，用式(3)计算得到轴重A1;

步骤3将计算的轴重A1作为已知量，基于影响线算法，用式(5)计算得到新的影响线I1;

步骤4重复步骤2和步骤3的操作，直到轴重的计算结果收敛为止，即|An-An-1|≤ε。

相比于商用BWIM系统，桥梁动态称重迭代算法用于称重的影响线不是恒定不变的。在识别车辆轴重时，以基准影响线为依托，通过反复应用Moses算法和影响线算法不断地更新修正基准影响线，最终用更新后的影响线计算车辆轴重。从理论上讲，桥梁动态称重迭代算法求得的影响线能更好地匹配桥梁动力响应信号，更新后的影响线与车轴轴重的计算值拟合出的车桥动力响应理论值也将更好地吻合实测值。即桥梁动态称重迭代算法计算得到的车轴轴重更准确。

2 实桥试验

为了验证桥梁动态称重迭代算法的轴重识别精度，本文以湖南省怀化市的舞水五桥引桥作为研究对象进行相关研究。

2.1 桥梁概况

怀化舞水五桥引桥是一座跨度为40 m的简支梁桥。它由10片T梁组成，桥宽24 m，双向四车道，两侧分别设有非机动车道和人行道，具体设计参数详见文献[13-14]，桥梁的示意图如图1所示。

2.2 试验方案

试验选定一辆两轴车作为加载车。加载车总重28.5 t(前轴重7.4 t，后轴重21.1 t)，轴间距4.7 m。在试验过程中，加载车以30 km/s以内的车速反复从车道三驶过，共10次。

在试验过程中，在跨中截面两侧的翼缘板下安装车轴探测传感器(free-alxe-detector,FAD)获取车辆类型、轴数、轴距及车速等信息；在主梁跨中截面的每片T梁底部安装动态应变传感器作为称重传感器，用于识别车辆轴重，如图1所示，具体位置详见龙波的研究。试验采用扬州科动KD4001工具式应变传感器和日本TML公司的DC-204动态信号采集仪记录车辆驶过桥梁产生的动态应变信号。数据的采样频率为200 Hz。现场试验测试系统如图2所示。

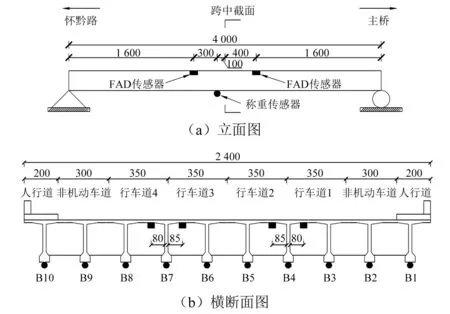
图1 怀化舞水五桥引桥示意图[13] (cm)Fig.1 Schematic diagram of Wushui Fifth Bridge approach bridge (cm)

图2 试验测试系统Fig.2 Data acquisition system

3 结果与分析

本节基于怀化舞水五桥引桥的车桥动力试验，分别用商用BWIM算法和桥梁动态称重迭代算法进行车辆轴重识别，通过对比分析，验证桥梁动态称重迭代算法轴重识别的可靠性。

3.1 试验数据

试验过程中，桥梁翼缘板处的FAD传感器和跨中T梁处的称重传感器同时采集加载车驶过桥梁产生的动力响应信号。

图3为10组跑车试验中的一组信号。其中：图中的两条实线分别表示前后两个FAD传感器采集的信号。每个车轴经过时会产生一个峰值，利用已知的两个FAD传感器纵桥向间距，计算车辆的车速以及轴间距等信息。图中的点线表示跨中T梁位置所有称重传感器动力响应信号的总和。由于称重算法是一维算法，假定车辆荷载对桥梁动力响应(弯矩/应变响应)不受车辆横向加载位置的影响，因此，将称重传感器动力响应信号之和作为轴重识别的信号。

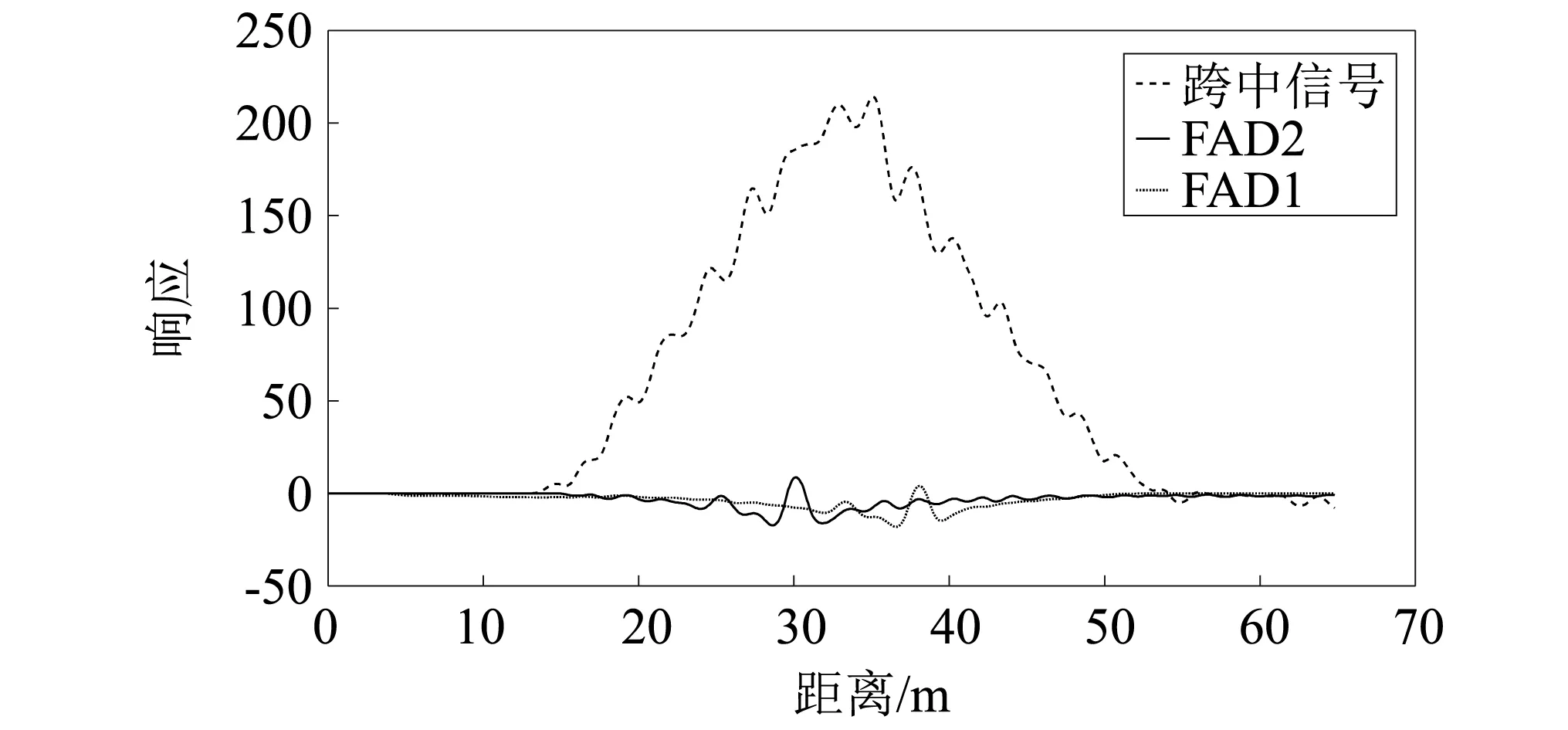
图3 车桥动力响应信号Fig.3 Vehicle-bridge dynamic response

3.2 轴重识别结果

在BWIM系统中，桥梁的实测影响线是车辆轴重识别的前提条件。通过上文介绍的影响线算法，计算得到每组车桥动力响应信号相对应的桥梁实测影响线，如图4所示。这里需要指出的是，考虑到车辆在上桥和下桥时会对桥梁的动力响应产生影响，在计算实测影响线时，在桥梁的前后两端各取10 m。即：影响线的总长度为60 m(10 m+40 m+10 m)。

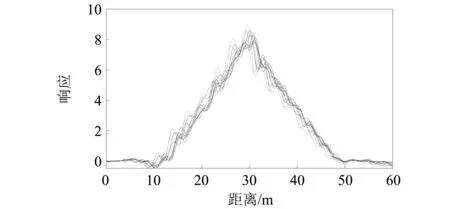
图4 实测影响线汇总图Fig.4 The calibrated influence lines

由图4可知，实测影响线总体的变化趋势相同，峰值相近，都为8左右。但是，每条实测影响线在局部略有不同，上下振动的方向不尽相同。为了全面地反映桥梁的动力特性，商用BWIM算法通常选取多条影响线的均值用于车辆轴重识别。因此，本文选取所有实测影响线的均值分别用两种算法(商用BWIM算法和桥梁动态称重迭代算法)对所有的车桥动力响应信号进行车辆轴重识别，计算结果如表1所示。

表1 不同算法的车辆轴重识别误差汇总表Tab.1 Summary of vehicle axle weight identification errors with different algorithms %

由表1可知：①对于商用BWIM算法，单轴轴重和总重识别误差的平均值都较低，分别为2.0%(前轴)、-0.7%(后轴)和0%(总重)。但是，单轴轴重的识别误差不稳定。其中，前轴识别误差变化的区段为[-47.0%，96.2%]，最大的误差接近了100%，导致其误差的标准差较高，达到了49.0%。相比之下，后轴的识别误差也较大，与相应前轴误差的大小相近，方向相反。以第三组的计算结果为例，前轴的误差为5.69 t(7.4 t×76.9%=5.69 t),后轴的误差为-5.32 t(21.1 t×-25.2%=-5.32 t)，相应总重的误差为0.37 t。这使得总重误差的变化范围较小，为[-1.5%，1.3%]，相应的标准差为0.9%。由此可知，商用BWIM算法车辆总重的识别精度较高，单轴轴重的分配不合理，识别精度较差。②对于桥梁动态称重迭代算法，车辆总重识别精度较高，其误差的均值和标准差都较低，分别为0.1%和0.9%。相比之下，单轴轴重的识别精度稍差。其中：前轴轴重的计算值一般小于真实值，其误差变化范围为[-30.8%，0.1%]；而后轴轴重计算值普遍大于真实值，其误差范围为[-0.5%，9.7%]。前轴轴重误差的均值和标准差都大于后轴轴重，数值上是相应后轴轴重误差的3倍左右。③对比两种算法发现，车辆总重误差的均值和标准差都较低。这表明两种算法的总重识别精度都达到了较高的水平。对于单轴轴重，虽然桥梁动态称重迭代算法单轴轴重误差的均值大于商用BWIM算法，但商用BWIM算法计算得到的单轴轴重误差绝对值都不小于桥梁动态称重迭代算法的计算误差。以第一组数据为例，桥梁动态称重迭代算法的轴重误差绝对值(前轴1.2%，后轴0.5%)明显低于商用BWIM算法的计算误差(前轴47.0%，后轴14.4%)。此外，桥梁动态称重迭代算法单轴轴重计算误差的标准差(前轴10.8%，后轴3.2%)也明显低于商用BWIM算法(前轴49.0%，后轴16.3%)。由此说明，相比商用BWIM算法，桥梁动态称重迭代算法能显著改善车辆轴重识别的精度。

3.3 分 析

为了研究桥梁动态称重迭代算法改善轴重识别精度的原理，以表1中的第三组数据为例，绘制出每次迭代称重后相应的轴重，如图5所示。图中的点线表示车辆轴重的真实值，实线表示每次迭代计算后的车辆轴重。这里需要指出的是，当迭代次数为0时，桥梁动态称重迭代算法等效于商用BWIM算法，即：轴重的计算值与商用BWIM算法的计算值相同。

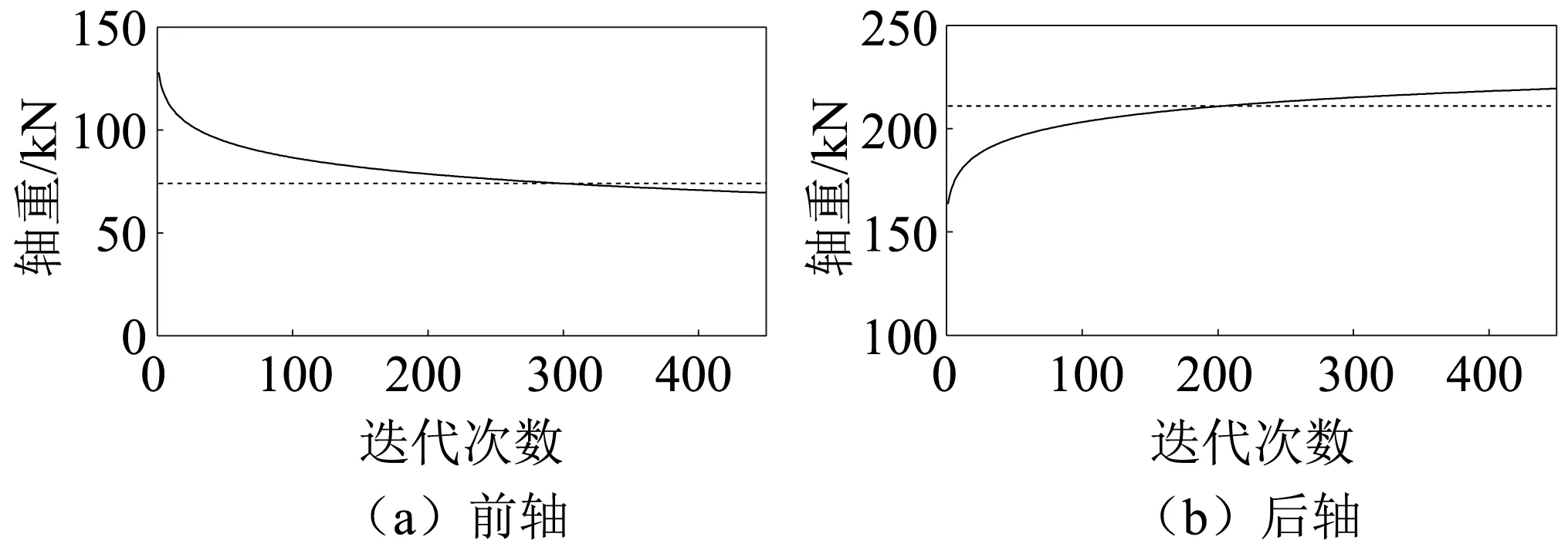
图5 迭代过程中轴重变化图Fig.5 Axial weight change diagram during iteration

由图5可知：在迭代计算过程中，轴重前期变化的较快，曲线的斜率较大；当迭代次数达到30以后，每次迭代的轴重变化率越来越小，曲线趋于平缓，直到计算结果收敛为止。相比于初始轴重(商用BWIM算法的轴重结果)，轴重不断向实际轴重值靠近，最终在实际轴重附近收敛。

在轴重计算的过程中，轴重变化的同时，桥梁的实测影响线也在不断更新，其变化过程如图6所示。为了较全面地反映实测影响线的变化过程，图中分别绘出了初始(基准)影响线ILo(所有实测影响线的均值)、迭代1次的影响线IL1、迭代30次的影响线IL30、最终的影响线ILe以及第三组实测车桥动力响应所对应的实测影响线ILs。

由图6可知：①基准影响线与第三组实测车桥动力响应所对应的实测影响线有较大差异。这是由于ILo是所有实测影响线的均值，消除了影响线中部分的车桥动力效应，使得ILo曲线比ILs曲线更加平缓，振荡更少。ILo的最大峰值(7.89)明显低于ILs(8.94)，这导致由ILo计算出的轴重偏大。②经过第一次迭代计算，更新后的影响线IL1形状发生较大变化。IL1的峰值曲线变的更陡峭，波峰和波谷的位置也发生了细微的改变。这是由于实测车桥动力响应含有较明显动力效应(见图3)，利用已知A1计算出的影响线IL1比ILo包含更多的动力信号，影响线IL1的相位角信息(波峰和波谷所在的位置)更贴合实测车桥动力响应的变化规律。③随着迭代次数的增加，更新后的影响线的峰值逐渐向ILs靠近，最终收敛于ILe。ILe和ILs曲线的变化规律相同，各个峰值点的数值相近，因此，由ILe计算得到的轴重与真实轴重相近。

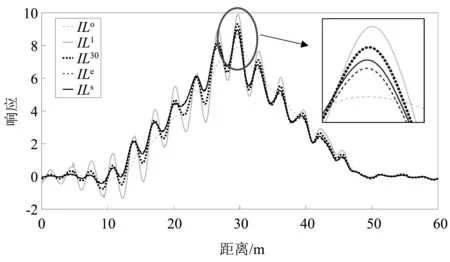
图6 迭代过程中影响线对比图Fig.6 Influence line comparison diagram during iteration

3.4 讨 论

由上文可知，在轴重识别过程中，桥梁动态称重迭代算法通过基准影响线不断迭代更新，得到与实测车桥动力响应较完美匹配的影响线，由此便可计算出与真实值相近的车辆轴重。为了探究基准影响线的选取对轴重识别精度的影响，本节分别以10组实测影响线为基准影响线对所有的实测车桥动力响应进行轴重识别，计算结果如表2所示。表中序号表示轴重识别采用的基准影响线号码。以序号1为例，它表示以第1组车轿动力响应所得的实测影响线作为基准影响线，对所有车轿动力响应进行动态称重，得到轴重识别误差的平均值和标准差。

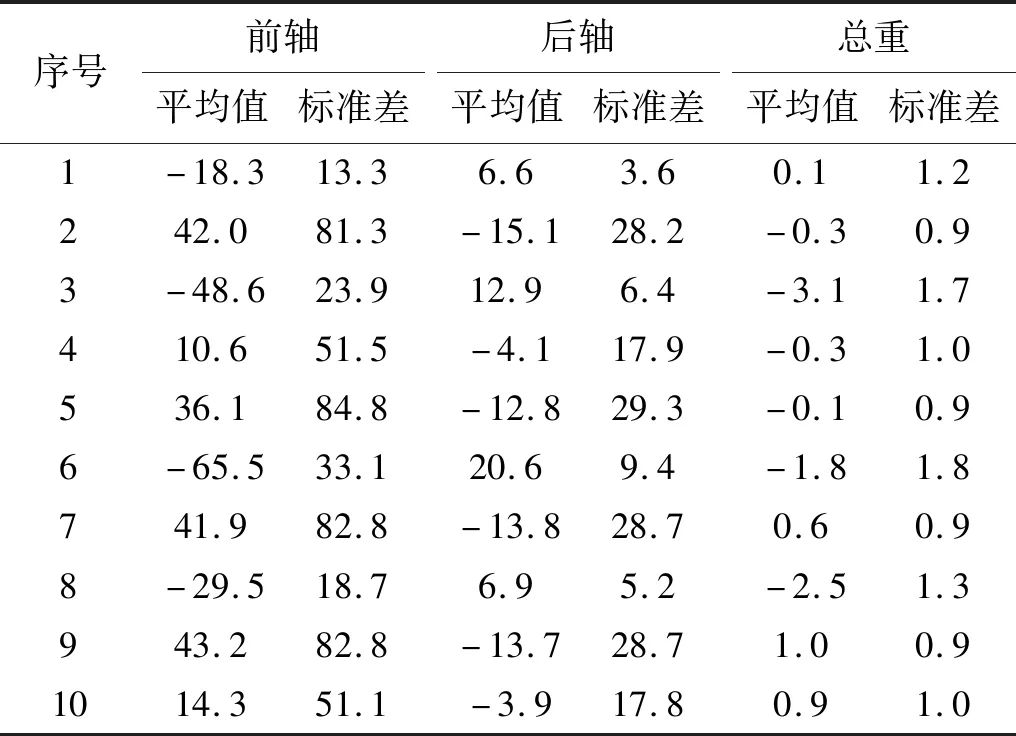
表2 不同基准影响线对应的车辆轴重识别误差汇总表 Tab.2 Summary of vehicle axle weight identification error corresponding to different baseline influence lines %

由表2可知：不同的实测影响线作为基准影响线进行轴重识别，计算结果的精度存在一定差异。以前轴为例，轴重识别误差平均值的范围为[-65.5%,43.2%]，其中，绝对值最小的误差平均值是选用4号实测影响线进行轴重识别的结果，达到了10.6%。而最大的绝对值选用的是6号实测影响线，达到了-65.5%。对比表1发现，表2的计算结果都要高于以影响线均值作为基准影响线的计算误差。这说明单一车桥动力响应提取出的实测影响线不能较全面的反映桥梁的力学特性，若直接用于桥梁动态称重迭代算法，无法迭代更新出与所测车桥动力响应相匹配的影响线，将不能得到较高精度的车辆轴重。因此，桥梁动态称重迭代算法宜选用实测影响线的均值作为基准影响线进行轴重识别。

4 结 论

为了改善BWIM系统的轴重识别精度，本文提出了一种新的桥梁动态称重算法——桥梁动态称重迭代算法。基于怀化舞水五桥引桥的车桥动力试验，分别对商用BWIM算法和桥梁动态称重迭代算法进行轴重识别，进行对比分析，得出如下结论：

(1)实桥试验的计算结果表明，商用BWIM算法可以得到较高精度的总轴重，但其单轴轴重识别的精度较差。

(2)相比于商用BWIM算法，桥梁动态称重迭代算法通过反复应用Moses算法和影响线算法，更新基准影响线，使其能更好地匹配车桥动力响应，从而计算出误差更小的车辆轴重。

(3)桥梁动态称重迭代算法中，选用不同的实测影响线作为基准影响线，轴重识别的精度存在一定的差异。其中：最能反映桥梁真实力学特性的均值影响线能够在轴重识别过程中得到较高的精度。

(4)桥梁动态称重迭代算法更新迭代出的影响线包含更多桥梁信息(如：车桥耦合信号、噪声信号、路面不平整度等)，后续可用于桥梁安全评定。