漂珠聚氨酯复合泡沫力学特性及本构模型研究

张冰冰,赵金安,薛仲卿,卢亚菁,范志强

(1.太原工业学院 环境与安全工程系，太原 030008；2.中北大学 理学院，太原 030051 )

粉煤灰漂珠是电厂燃烧产物煤灰的主要成分，为典型的轻质中空球壳材料，具有良好的物理和力学特性。我国年产3～5亿吨粉煤灰工业固废，目前主要应用于建筑工程的隔热结构[1-2]，亟需拓展其高效综合利用途径。当前研究表明中空微珠作为造孔剂填充高聚物和金属基体时，可制备具有优异力学性能的轻质泡沫，如玻璃微珠填充环氧树脂、铝等基体制备的复合泡沫，因具有优异的力学、隔热和耐磨性能被广泛应用于航空航天和车辆工程[3-5]，然而有关粉煤灰漂珠复合泡沫的相关研究却较少。将漂珠引入熔体发泡法制备的复合泡沫铝具有更低的密度和更高的比强度，且材料应变率效应等动态力学特性也显著改善[6]。分析可知漂珠作为脆性空心微珠在传统泡沫铝胞元壁上引入了更多的微缺陷，降低孔壁密度的同时增强其脆性特征，从而导致了上述有益效果。另外，文献[7]以大尺寸粉煤灰漂珠为主要组分，以聚氨酯为多孔黏结剂制备了一种具有多级闭孔胞元的漂珠聚氨酯复合泡沫(cenospheres polyurethane syntactic foams，CPSFs)，初步的静动态力学性能实验表明CPSFs具有较高的比性能和应变率效应，在轻质抗爆炸/冲击结构设计中具有较大的应用潜力。

传统复合泡沫往往由一种或多种不同尺寸的空心微珠填充高聚物基体制备，仅包含一级微孔结构。CPSFs则具有漂珠腔体、胞壁微孔和黏结剂胞元多级不同尺度的复杂微结构，力学特性随材料组分、加载速度等因素体现出较为复杂的依赖规律。考虑到粉煤灰漂珠作为CPSFs的主要成分，其几何和力学性质对泡沫力学特性的影响机制尚不清楚，且以往研究并未构建该类复合泡沫的力学模型，不利于结构设计中材料选型、数值仿真等后续工作的开展。因此，本文针对漂珠尺寸和蜂窝铝增强相对CPSFs的力学性能和变形行为的影响规律开展系列准静态压缩实验，在此基础上采用Avalle理论构建CPSFs的力学模型，为该材料基本力学特性的预测提供理论参考。

1 CPSFs压缩实验

本文使用两种尺寸的粉煤灰漂珠颗粒，平均外径和壁厚分别为450 μm和30 μm、950 μm和50 μm，堆积密度约为0.35 g/cm3，表观密度分别为0.625 g/cm3和0.58 g/cm3。利用XRF测得这两种漂珠的主要化学组分为SiO2、Al2O3和Fe2O3，对应的质量分数分别为35%，15～26%和20%。通过SEM观测两种粒径漂珠的微观形貌可知，两种漂珠外观大致呈球体，表面粗糙，如图1(a)所示。然后，以硬质聚氨酯为黏结剂在常温下通过压力渗透法制备成普通复合泡沫LT和LG，可看出粉煤灰漂珠比较均匀地分布在复合泡沫当中，聚氨酯泡沫完全充满于整个试样，如图1(b)所示。为改善材料力学行为，采用厚度为0.06 mm铝箔制成的孔边长为4 mm的蜂窝铝作为增强相，对应增强泡沫为RLT和RLG，如图1(c)～(f)所示。本文所制备的LT、RLT、LG、和RLG四种复合泡沫密度范围为0.48～0.72 g/cm3。压缩实验采用SUNS材料万能试验机，传感器最大负荷100 kN，试样直径30 mm，高度22～30 mm，以约2.0 mm/min速度对试样进行准静态压缩，每组实验结果取三次有效重复实验的平均值。在准静态压缩过程中，通过GOM 5M三维数字散斑测量系统观测试样变形并进行数字图像相关分析(digital image correlation，DIC)。

图1 粉煤灰漂珠微观结构及四种类型复合泡沫Fig.1 Microstructure of fly ash cenospheres and four types of syntactic foams

2 实验结果与分析

2.1 基本力学行为

图2分别是密度约0.54 g/cm3和0.63 g/cm3的四种类型复合泡沫的工程应力应变曲线。由图可知，所有曲线均具有泡沫材料典型的三个变形阶段：线弹性、平台段和致密化段，且强度和平台应力均随密度的增大而增大。与普通复合泡沫LT和LG相比，相同密度下含增强相复合泡沫RLT和RLG分别有更高的压缩强度和平台应力，且致密化应变随密度增大而略有减小。

由图2可知，对于密度为0.54 g/cm3的四种复合泡沫(RLT、RLG、LT、LG)，漂珠尺寸对其平台应力的影响较小，含增强相的CPSFs(RLT、RLG)的强度和平台应力比普通复合泡沫(LT、LG)分别提高约19.1%～28.0%和8.2%～11.6%；对于密度为0.63 g/cm3的四种复合泡沫，RLT的力学性能最高，RLT和RLG整体力学性能明显优于LT和LG，其强度分别提高约44.8%和14.5%，平台应力分别提高约45.3%和15.6%，表明漂珠尺寸、泡沫密度和增强相对复合泡沫基本力学性能的影响规律较为复杂。综合对比两种密度下的CPSFs，发现其力学特性随密度增大而增强，随漂珠尺寸减小也出现增强现象。为深入研究复合泡沫力学行为，在压缩过程中通过捕捉其变形过程，利用数字图像相关技术进行处理得到密度为0.58 g/cm3的LT和RLT轴向压缩位移场，如图3所示。

图2 四种复合泡沫典型工程应力应变曲线Fig.2 Typical engineering stress-strain curves of the four types of CPSFs syntactic foams

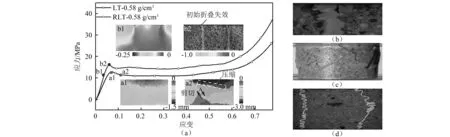
图3 普通和增强泡沫的轴向压缩行为Fig.3 Uniaxial compression behavior of the plain and reinforced syntactic foams

由图3可知，LT曲线的a1～a2段出现一个轻微的应力降低过程，并且图中a2出现明显的剪切变形带，将位移场分割成若干部分。将二者联系起来，不难发现剪切破坏是导致其出现强度失效和压力降的原因，而剪切失效的产生主要是由于聚氨酯黏结剂的破坏所致。图3中RLTs曲线在线弹性段之后也出现一段应力软化段，结合图中b1、b2可知，该现象主要由铝箔初始受压屈曲变形导致其压缩强度失效和后续压溃行为，初始折叠失效细节如图3(b)所示。LT的宏观压溃以剪切破坏为主，如图3(c)所示，而增强泡沫中金属薄壁结构的折叠抑制了复合泡沫的剪切失效，从而导致其宏观变形以轴向压溃为主，压缩后增强泡沫的剖面如图3(d)所示。为进一步考察复合泡沫的失效和铝蜂窝的增强机制，分析LT和RLT材料在初始压溃阶段的轴向压缩应变场，分别如图4和图5所示。从图4可知，由于复合泡沫内部微结构的不均匀性，材料在线弹性段的压缩应变即表现出典型的不均匀性，材料局部产生应变集中现象。细观结构的应变集中随材料的压缩过程逐渐发展并演化为典型的宏观应变集中带，如图4(c)所示。由图可知，强度较低的漂珠更容易卷入变形集中带，这些随机分布的变形集中带主要造成材料的初始剪切失效，这与漂珠/高聚物复合泡沫的失效模式基本一致[8]。

图4 LTs轴向压缩应变云图Fig.4 Axial strain contours of LTs at different stages

图5(a)为RLT在初始压溃阶段的轴向应变场，图中CA和CB分别为试样中靠近边缘和靠近中心区域的蜂窝胞孔内的复合泡沫，即CA的侧向约束较差，CB周围受蜂窝的侧向约束较强。实验过程中发现不同约束下的CPSFs呈现不同的失效机制。为进一步分析其差异，对比两个不同蜂窝铝单元内部的子区域CA和CB的变形过程，如图5(b)和图5(c)所示。其中b1和c1分别是CA、CB区的轴向应变场，b2和c2为对应的位移场，此时对应的试样工程应变约5%，约对应材料失效应变。

由图5(b)可知CA区域的复合泡沫呈典型的剪切失效模式，其位移场被滑移线分割为典型的子区域，其中“C”和“S”分别代表轴向压缩和剪切应变集中带，应变剪切带主导CA区域内CPSF的失效模式。在侧向约束效应较强的CB区域内，更容易形成左右对称或者趋近于水平分布的压缩变形带。总结可知，CPSFs与多数空心微珠填充高聚物形成的复合泡沫类似，在准静态轴向压缩下的主要失效模式为剪切破坏。然而，当材料内部引入纵向薄壁结构作为侧向约束时，材料被分割为若干个棱柱，各子区域内的复合泡沫受侧向约束作用更容易产生轴向压溃变形模式[9]，因此铝蜂窝的增加改变了CPSFs内部主导性失效模式，材料压缩变形机制的转变改善了复合泡沫的力学性能。

图5 RLTs轴向压缩应变和位移场演化过程Fig.5 Evolution of the axial strain and displacement fields of RLTs

2.2 密度和漂珠尺寸对力学特性的影响

图6为四种类型CPSFs的强度与平台应力随密度变化关系，图6(a)为四种类型CPSFs的压缩强度与相对密度呈y=αxβ的关系，图中虚线是压缩强度随相对密度变化趋势的拟合曲线。相对密度计算采用ρr=ρ/ρ*，其中：ρ为复合泡沫名义密度；ρ*为基体密度，通过结构细观组分分析可知材料等效基体密度约为1.8 g/cm3[10]。α和β是拟合系数，具体拟合结果见表1。

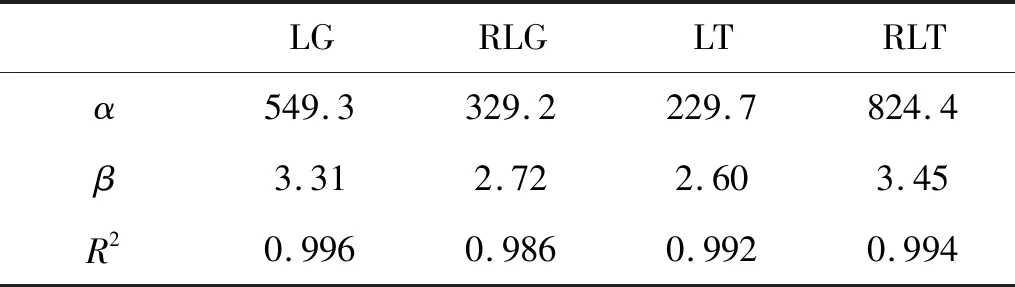
表1 强度随密度变化趋势的拟合系数Tab.1 Fitting coefficient of strength variation trend with density

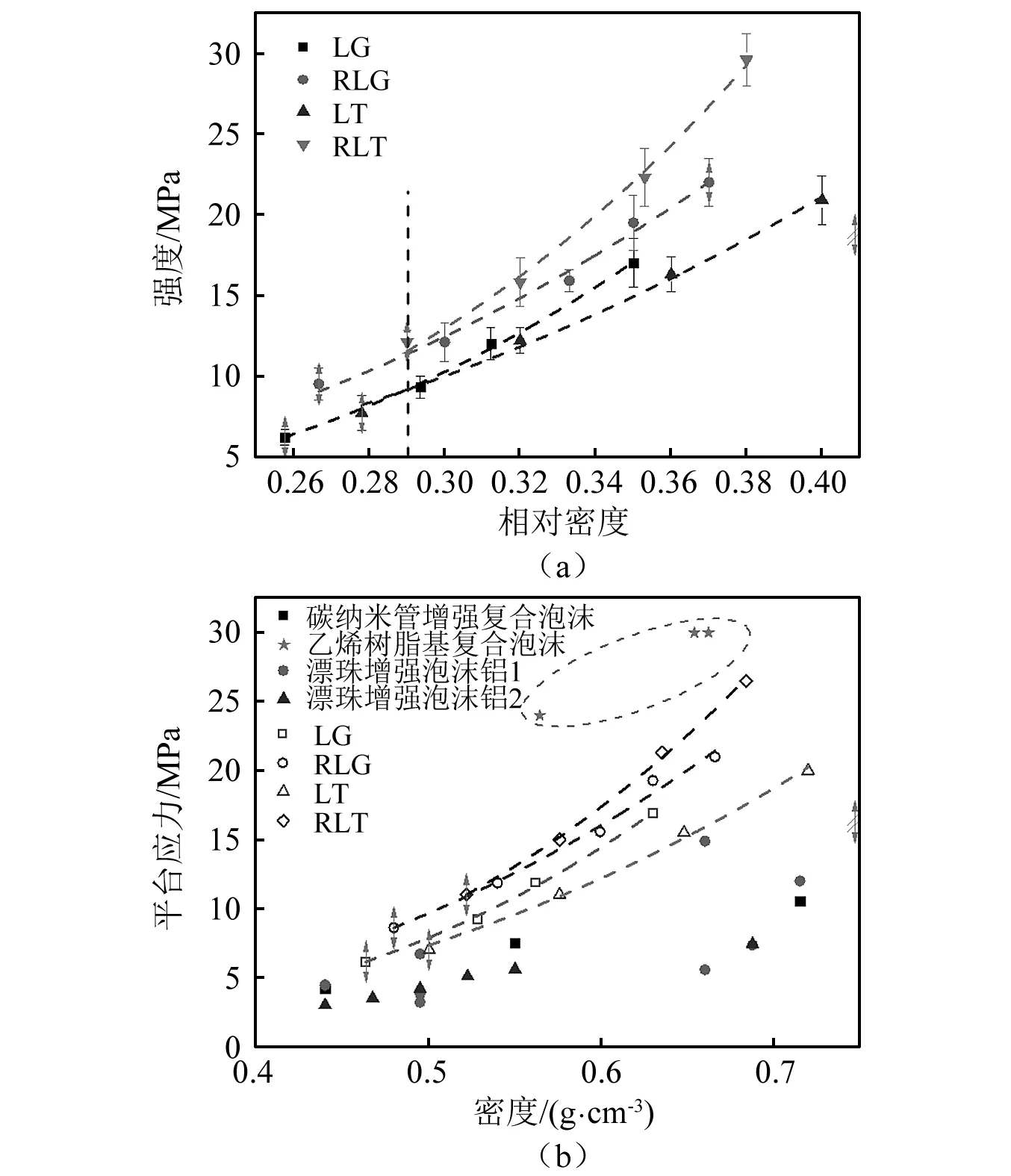
图6 CPSFs强度与平台应力随密度变化关系Fig.6 Relationship between CPSFs strength and platform stress with density

强度是衡量材料抵抗破坏的重要指标，图6(a)为四种复合泡沫的强度随相对密度的变化规律，可知RLT的强度随密度的增长率最高，LT的增长率最低。LG和RLG强度随密度的增加趋势基本一致。当材料相对密度低于0.29时，漂珠尺寸对复合泡沫的压缩强度几乎没有影响；当相对密度大于0.29时，漂珠尺寸较大的复合泡沫LG的强度略高于LT。对于含增强相的复合泡沫RLG和RLT而言，在该密度范围内漂珠尺寸较小的RLT性能更优异。相同密度下RLG比LG的强度值高约2.2 MPa，前期实验测得蜂窝铝的压缩强度约2.15 MPa，由此可知RLG的增强效果主要归因于复合泡沫中蜂窝铝的添加。在相对密度0.29～0.38内，RLT与LT的强度差值从2.5 MPa提高到10.8 MPa，RLT的压缩强度存在显著的额外增强效应，分析认为这主要是由RLT中CPSF的变形机制的转变所致。总之，对于RLT而言，随材料密度增大蜂窝铝的增强机制越明显，但该增强机制同时受漂珠尺寸的影响。

平台应力是决定泡沫材料吸能特性的重要因素。由图3可知，含增强相复合泡沫的平台应力往往低于其压缩强度，这是由复合泡沫中蜂窝铝受压弯曲折叠导致出现应力软化现象。而普通复合泡沫的平台应力和压缩强度接近。图6(b)是该实验所用四类复合泡沫与文献中几种新型泡沫材料平台应力的对比图[11-12]。由于与所对比的复合泡沫基体密度均不相同，因此图示横坐标为材料名义密度。如图所示，本文四种复合泡沫的平台应力均低于乙烯复合泡沫，这主要由于CPSFs是由聚氨酯泡沫基体和相对较大的漂珠颗粒组成，较多的孔隙导致其承载力较低。然而，本文所提供的复合泡沫具有更大的致密化应变，同时与新型碳纳米管和漂珠增强的泡沫铝相比具有更大的平台应力和能量耗散特征，计算可知，当前密度范围内的普通和增强CPSFs的比吸能分别约为3.6 ～ 10.8 MJ/m3和 4.2～13.0 MJ/m3。

3 Avalle本构模型

复合泡沫由于材质组分、细观结构复杂且往往存在较多的微缺陷，导致当前关于其力学性能的研究多在宏观尺度上给出统计性结果，其物理模型的构建较为复杂，因此往往采用唯象模型描述其应力应变响应特征。泡沫材料的唯象本构中Rusch模型[13]、Liu-Subhash模型[14]和Avalle模型[15]均可较为准确地描述泡沫材料压溃过程中典型非线性力学行为，其中Avalle模型因具有更简洁的物理意义和更广泛的密度描述区间被广泛应用，其具体形式为

(1)

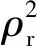
(2)

Avalle模型中的参数A表示应力应变曲线的平台应力(或屈服应力)，平台应力对密度的依赖性仍可参考Gibson模型，表示为ρr和ρ3/2的线性组合

(3)

模型中的参数B影响应力应变曲线的致密化应变，一般认为其与密度呈幂律关系

(4)

m，n与材料的相对密度无关，与复合泡沫种类相关。本文四种类型的复合泡沫通过最小二乘法对准静态压缩实验所得应力应变曲线进行拟合，在相对密度0.25～0.42内，可得到Avalle本构方程参数A，B，E，m，n的值见表2。

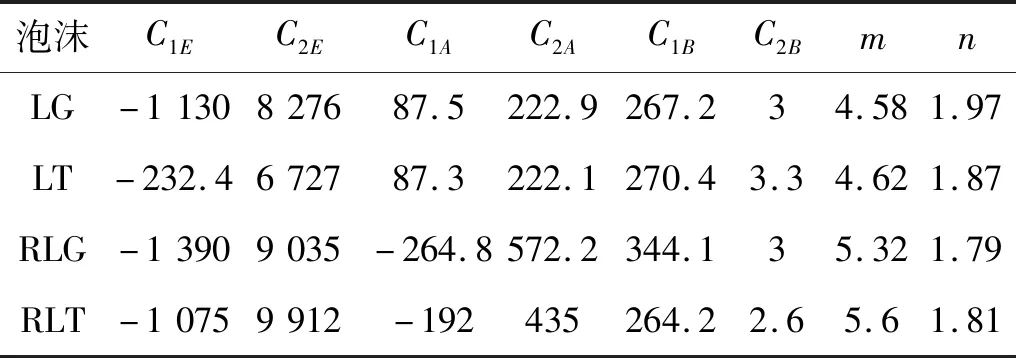
表2 四种类型复合泡沫Avalle本构拟合参数值Tab.2 Fitting parameters of Avalle constitutive model of four types of syntactic foams

通过实验数据得到的Avalle本构方程参数，分别对参数E和A进行对比分析，结果如图7所示。由图可知，四种类型复合泡沫的E和A均随材料的密度增大而增大，且含增强相的RLG与RLT的值均高于LG和LT，体现出蜂窝铝的显著增强作用，表征弹性模量和平台应力的参数随密度的变化趋势与实验结果基本一致，说明该拟合参数能够较为准确地表征材料基本力学性能随密度的变化规律。

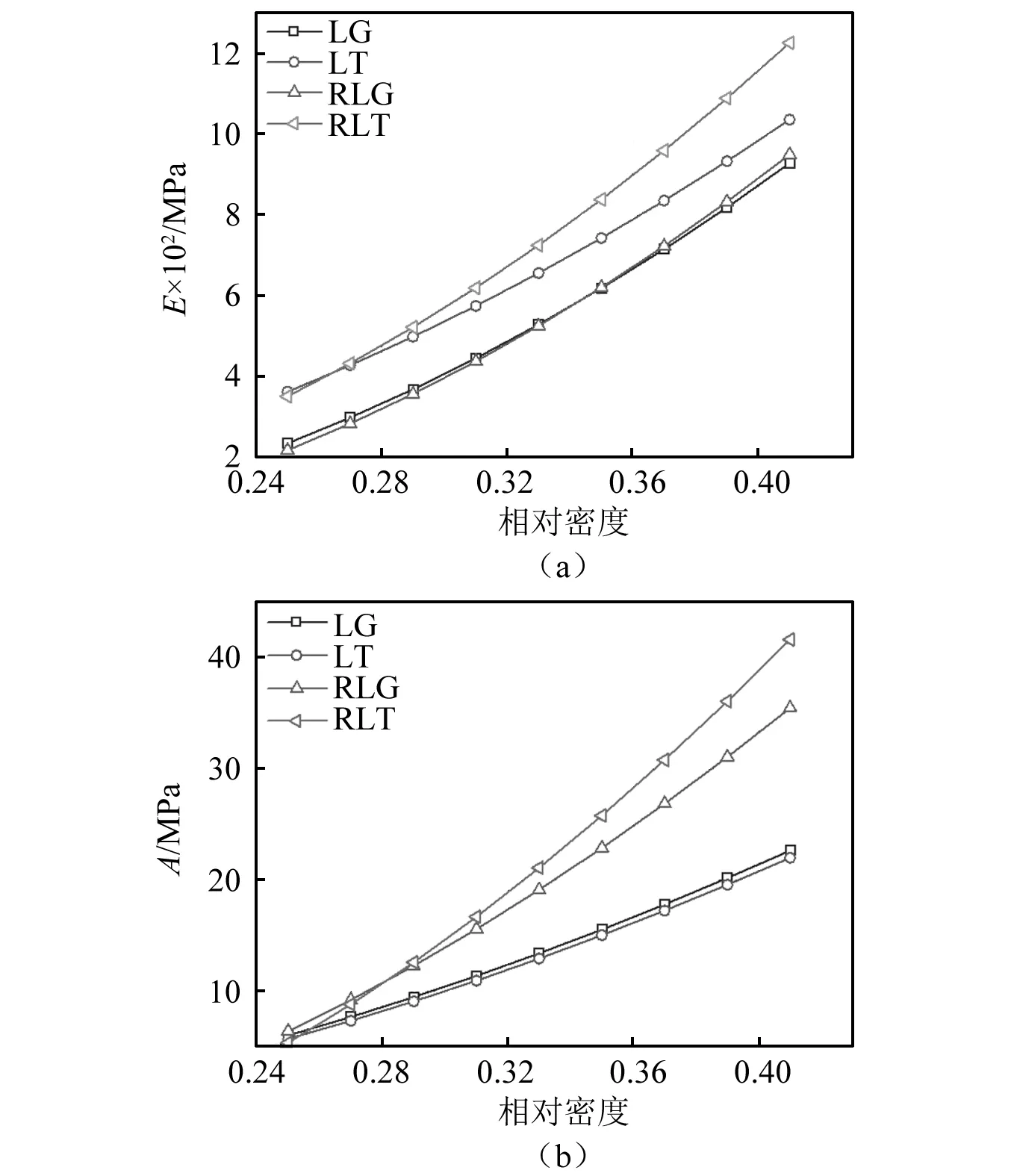
图7 复合泡沫Avalle模型参数与密度的关系Fig.7 Relationship between parameters of Avalle model and the density of CPSFs syntactic foams

将Avalle模型拟合的应力应变曲线与实验结果进行对比，如图8所示，拟合误差按e=σfit-σexp计算。其中：σfit为本构模型拟合应力；σexp为准静态实验测得应力。

由图8可知，Avalle本构方程拟合曲线与实验所得应力应变曲线宏观上基本一致，能描述其典型的弹性阶段、应力平台段和致密化阶段这典型三阶段。对比发现，对于LG和LT复合泡沫，实验与拟合结果吻合度较高，平台应力段误差小于2 MPa，线弹性段与致密化段误差均小于5 MPa。对于RLG和RLT复合泡沫，应力平台段和致密化段误差均小于4 MPa，而弹性段屈服强度处(ε=0.05～0.10)误差略大，这主要是由于Avalle模型采用了连续方程描述材料在不同阶段的力学行为，其弹性段至应力平台段为平稳过渡形式。然而，实验中由于铝蜂窝增强相的存在，RLT和RLG的强度往往高于平台应力，在初始压溃阶段存在典型的应力降低“软化”现象，Avalle本构模型并不能描述该物理机制，但在平台应力和致密化阶段，模型仍然能够在较大密度范围内描述其应力应变行为。

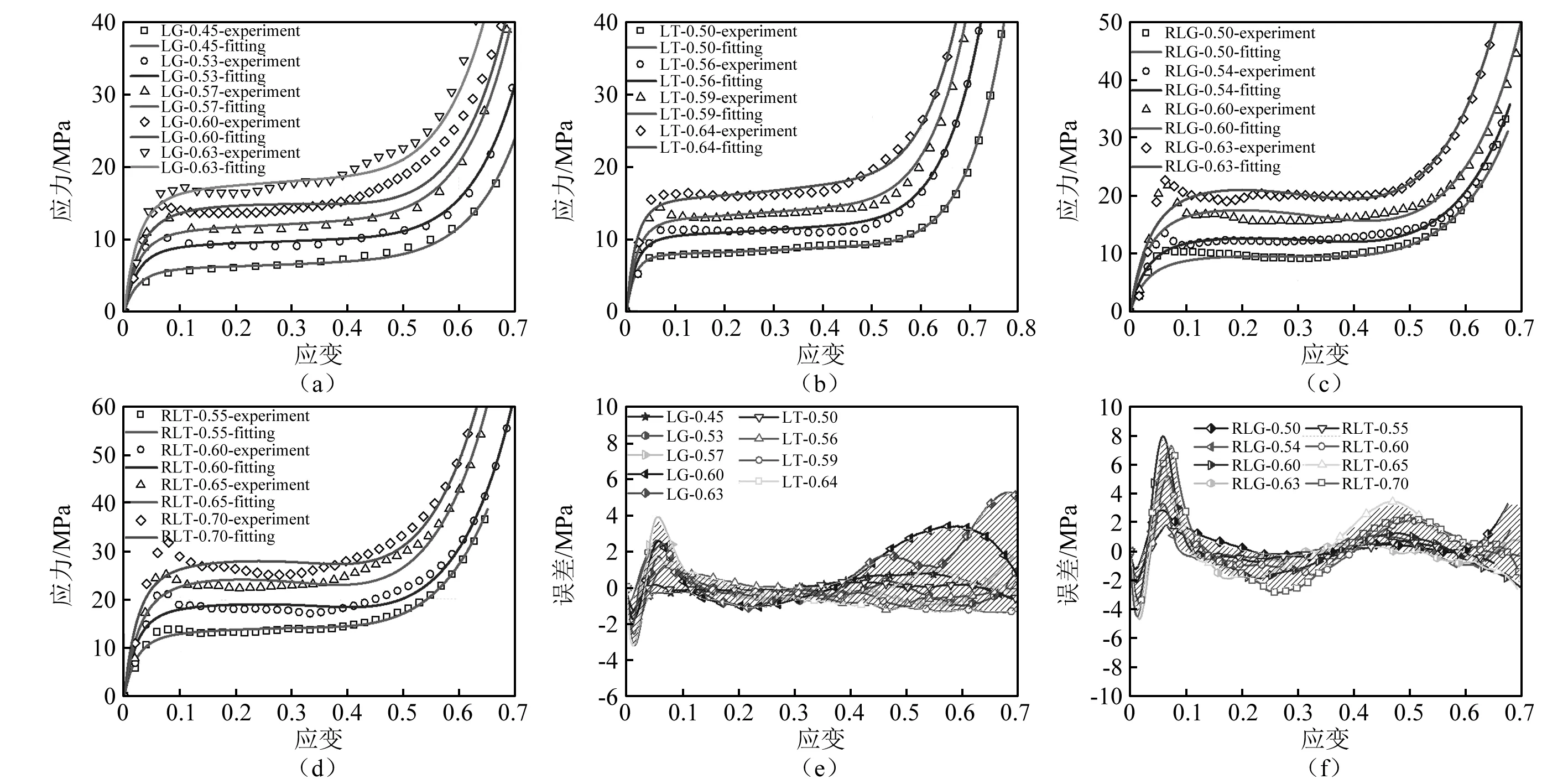
图8 复合泡沫应力应变曲线拟合与实验结果对比Fig.8 Comparison of stress-strain curves between fitting and experimental results of CPSFs syntactic foams

在实际工程设计和数值仿真中，泡沫材料主要作为填充吸能芯体，一般不作为单独承载组件，因此模型能够准确预测其能量吸收行为更为重要。为进一步考察Avalle本构方程的适用性，对比分析了这四种复合泡沫的体积比吸能W

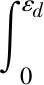
(5)

由图9可知，Avalle拟合曲线的体积比吸能与实验所得数据吸能曲线重复度极高。这是因为对吸能影响比较重要的是应力应变曲线的平台段，而屈服强度和致密化段的误差对体积比吸能几乎不产生显著影响，表明Avalle本构方程能够拟合预测这四类复合泡沫的准静态压缩曲线。

图9 Avalle模型对复合泡沫能量耗散特性的拟合结果Fig.9 Avalle model fitting results of energy dissipation properties of CPSFs syntactic foams

4 结 论

本文以工业固废粉煤灰漂珠为主要组分、以铝蜂窝为增强相制备了具有不同密度和漂珠尺寸的新型复合泡沫材料，通过准静态压缩实验研究了密度和漂珠尺寸对该类复合泡沫力学性能的影响，探讨了铝蜂窝的增强机制，然后基于Avalle本构模型对该类复合泡沫应力应变曲线进行拟合，结论如下：

(1)当复合泡沫的相对密度小于0.29时，漂珠尺寸对其抗压强度和平台应力的影响较小；当材料相对密度大于0.29时，漂珠尺寸较大的普通复合泡沫和漂珠尺寸较小的增强型复合泡沫具有更好的力学性能。

(2)普通和增强复合泡沫的主要失效模式均受内部随机分布的变形集中带影响，但普通复合泡沫主导性失效模式为剪切破坏，而含有增强相的复合泡沫主导性失效机制转变为轴向压缩。

(3)漂珠聚氨酯复合泡沫中铝蜂窝的增强机制主要为材料变形模式的转变，但该增强机制同时受漂珠尺寸的影响；包含较小漂珠的复合泡沫内，该变形机制的转变效果更为显著。

(4)Avalle唯象本构模型能够较为准确地预测漂珠聚氨酯复合泡沫的准静态压缩响应，对铝蜂窝增强复合泡沫的强度描述误差较大，但对四类复合泡沫能量耗散行为的描述与实验结果较为吻合。