粗化床面非均匀沙推移质运动扩散特性研究

刘春晶，曹文洪，耿 旭，许琳娟

（1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室，水利部水沙科学与江河治理重点实验室，北京 100048；2.黄河水利委员会黄河水利科学研究院，河南 郑州 450003）

1 研究背景

近底床面是推移质运动的主要区域，也是水流紊动产生和发展最为活跃的区域，水沙动量和能量交换频繁，推移质颗粒运动是其与近壁区水流紊动相互作用外在表现。大量试验观测表明，与水流的紊动类似，推移质颗粒运动存在一定随机特性。1930年代开始，Einstein根据泥沙随机运动特性建立了推移质输沙理论体系［1］，打开了以随机过程理论研究泥沙运动之门，之后大量学者从颗粒运动特性角度开展推移质研究，其中颗粒的扩散特性一直是这方面研究的热点［2-7］。

布朗运动是花粉颗粒在水分子作用下的无规则运动，典型布朗运动遵循菲克扩散定律，同时为典型的马尔科夫过程［2］，颗粒未来运动状态只与当前状态有关，与历史状态无关，仅通过当前的运动状态就可以获知颗粒未来运动的全部信息。韩其为等假定泥沙颗粒运动遵循马尔科夫过程，将泥沙颗粒运动分为4种状态，提出泥沙颗粒未来运动可完全由当前状态与16个转移概率确定［3-5］；Ancey等在描述挟沙力时引入马尔科夫“生-灭”过程，即“生”和“灭”两个状态［6-7］，“生”表示泥沙被水流所挟带由静止状态转为运动，“灭”表示泥沙颗粒由运动转为静止；Furbish等建立了推移质颗粒运动通量主方程，认为颗粒通量可分解为对流项和扩散项，其中对流项与水流动力相关，扩散项与颗粒本身的随机运动相关［2］。Nikora等将泥沙颗粒运动分为小、中、大三个尺度［8］，其中小尺度为颗粒跳跃阶段，符合弹道扩散规律，中尺度为颗粒多个跳跃阶段，符合超扩散或正常扩散规律，大尺度为包括颗粒等待时间在内的更长的时间尺度，符合次扩散规律。Ganti等提出可以同时反映颗粒正常扩散和反常扩散的模型［9］；Martin等利用水槽试验证实了泥沙示踪颗粒运动的反常扩散现象［10］；Fathel等进一步分析了颗粒运动的特征［11-12］，并将颗粒运动与布朗运动进一步详细对比，认为泥沙颗粒运动类似于布朗运动中颗粒在单次碰撞之间的弹道运动，经过弹道扩散阶段后颗粒将回归正常扩散，不同于一般的反常扩散。范念念等认为在均匀沙条件下，根据不同的停止时间，泥沙颗粒运动可分别表现为次扩散、正常扩散和超扩散，非均匀沙总体上出现的弹道运动是由于沿程分选造成的，而非反常扩散造成［13-14］。近期，Liu等对低输沙率条件下颗粒运动参数进行统计，分析了颗粒停止时间随水流强度变化特征［15］；Ballio等研究了由于拍摄范围和时间观测限制对推移质运动参数统计结果的影响［16］；Ancey全面回顾了推移质研究进展，指出进一步深入理解颗粒运动内在的随机特性是未来准确估算推移质输沙率的基础［17-18］。

已有关于推移质扩散特性研究多基于平整床面和均匀沙开展，与天然河流实际情况存在一定差异。Zhu等关于粗化床面颗粒运动表明，在较小时间尺度下颗粒表现为超扩散，较大时间尺度下则表现为次扩散［19］。许琳娟等利用水槽试验分析了粗化床面条件下输沙率及颗粒运动分布特性［20-21］，本文以高速摄像机拍摄颗粒运动图像，建立颗粒图像与颗粒粒径之间的定量关系［22］，然后根据颗粒在连续帧的位置获取泥沙颗粒运动的速度、轨迹等信息，进而对泥沙颗粒运动的扩散特性进行分析。

2 试验简介

2.1 试验水槽和拍摄系统 试验在中国水利水电科学研究院大兴试验基地大型径流波浪水槽中进行。水槽长50 m，宽1 m，高1.2 m，边壁与底板均由玻璃板组成，可从侧面或底部观测泥沙运动。水槽坡度可调，变坡范围0～1%。

采用特制拍摄装置从水槽顶部对泥沙颗粒运动进行拍摄，如图1所示。该装置由平板小车、支撑架、两端翘起的玻璃板、吊装丝杠及照明灯管组成，整个装置可沿水槽移动。使用时将小车移动至所拍摄部位，调整丝杠吊装高度，使底部玻璃板刚好与流动的水面相接触。摄像机位于平板小车顶部，通过平板中央的拍摄孔对床面泥沙进行拍摄。底部玻璃板与水流直接接触，避免了由于水面波动而产生的拍摄成像不清问题。当水流速度较快时，玻璃板与水流接触面会有空气被吸入，在玻璃板中央形成较大气孔，影响床沙拍摄，为此在上游侧设置丝网，使进气孔破碎。

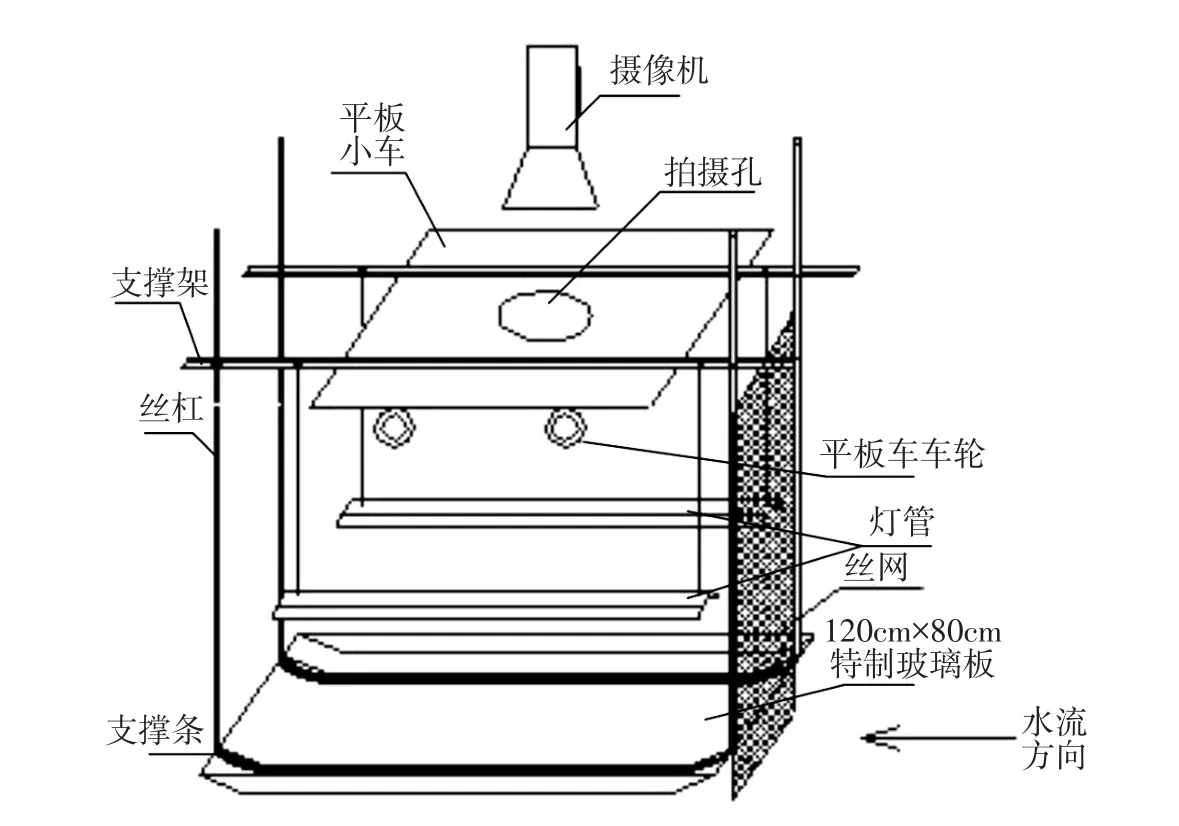
图1 颗粒运动拍摄装置示意

2.2 试验条件和数据提取 试验采用非均匀石英砂，粒径范围0.1～20 mm（颗粒级配如图2所示），水槽坡度4‰，流量110 l/s，试验粗化床面为170 l/s水流冲刷形成。摄像机分辨率1280×720 Pixel，拍摄速度50 fps，拍摄时长60 s。

图2 试验沙级配

表1为本文与已有颗粒扩散规律研究的试验条件对比。由表1可知，现有研究试验条件多为均匀沙，水流条件与天然河流相差较大，其中Furbish等［2］和Fathel等［11-12］的颗粒运动速度较小，仅为5 cm/s左右，而Martin等［10］和Ancey等［7］的水深较浅，仅为2 cm左右。本文非均匀沙粒径0.1～20 mm，水深约13 cm，水流流速约0.8 m/s，实测颗粒速度20 cm/s左右，与已有研究相比更接近天然河流实际情况。

表1 本文与其他研究试验条件对比

采用人工判读方法将60s拍摄观测范围内所有运动的颗粒按帧提取，共得到7000多个坐标，268个泥沙颗粒的运动信息［20-21］，泥沙颗粒粒径可根据其在图像中所占像素大小确定，粒径范围0.5～8 mm，如图3所示，其中大部分颗粒集中在2～3 mm之间。

图3 提取的运动颗粒粒径分布

3 结果分析

3.1 颗粒均方位移变化 以x方向代表水流运动方向，y方向代表与x方向垂直的横向方向。以颗粒在x方向的运动为例，xp(t)表示颗粒在t时刻的位置，则经过间隔时间τ后颗粒位移为［2，11］：

根据扩散方程，x方向的均方位移为：

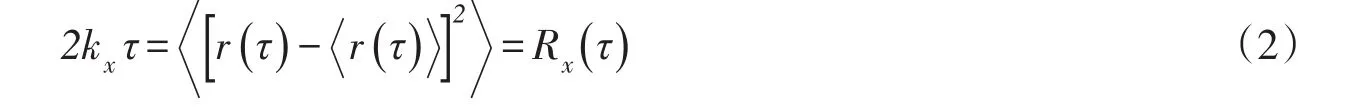
其中kx为颗粒扩散系数，颗粒均方位移与间隔时间之间的关系可表示为：

由式（3）可见，颗粒的均方位移与时间间隔之间为指数关系，指数α=1时表示颗粒运动符合正常扩散，0＜α＜1时扩散速度小于正常扩散，称为次扩散，1＜α＜2时扩散强度大于正常扩散，称为超扩散，α=2时为弹道扩散。

类似地，颗粒在与水流垂直的y方向运动也可以用式（1）—式（3）表示。此外，上式既适用于单颗粒运动分析，也用于大量颗粒运动分析。

根据式（3）计算了本文单颗粒均方位移变化情况，部分颗粒计算结果如图4所示，图中小标题No.表示颗粒序号，d为该颗粒的粒径，Rx(τ)、Ry(τ)分别表示颗粒在x方向和y方向的均方位移，其中图4（a）中泥沙颗粒x方向运动速度大于y方向，图4（b）、图4（c）中两个方向运动速度接近，图4（d）中泥沙颗粒x方向运动速度小于y方向。

由图4可知，粗化床面条件下单颗粒均方位移与平整均匀沙床面颗粒运动存在显著差异。在Furbish等［2］、Fathel等［11-12］试验中，时间尺度较小时均方位移曲线斜率几乎与 α=2 平行，Fathel等［11-12］据此将泥沙颗粒运动与布朗运动粒子相类比，认为颗粒运动在小时间尺度下表现为“类似弹道扩散”，后随着时间尺度增加以明显的反常扩散特征过渡到正常扩散。与上述结果不同，本文非均匀沙均方位移随时间间隔变化曲线斜率均处于1和2之间，一方面有可能是本文最小时间尺度较大，另一方面可能是由于粗化床面独特的边界条件所导致。在Furbish等［2］和Fathel等［11-12］的均匀沙试验中，泥沙颗粒在水流流向x方向的流速远大于横向y方向，x方向的均方位移约比y方向大一个数量级，与本文图4（a）接近。在本文粗化床面条件下，在近底床面存在与x方向具有一定夹角的优势“通道”，在“通道”中运动的颗粒y方向的流速有可能接近，甚至是超过x方向，如在图4（b）和图4（c）中x方向与y方向均方位移规律接近，在图4（d）中，y方向的均方位移已超过x方向。

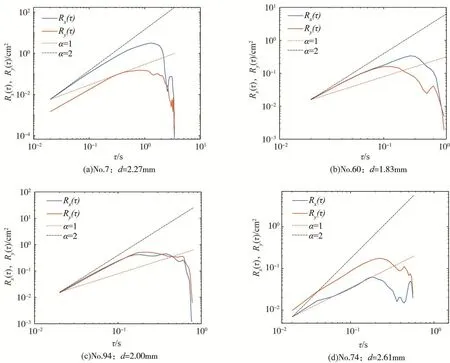
图4 部分单颗粒均方位移随时间间隔变化

为进一步分析非均匀沙运动特性，将颗粒按粒径大小分为7组，分别为＜1.5 mm、1.5～2 mm、2～2.5 mm、2.5～3 mm、3～3.5 mm、3.5～4 mm和＞4 mm组，计算了各粒径组所有颗粒的均方位移变化特征，图5列出了两组典型计算结果，图6为本文全部颗粒的均方位移变化特征。由图5和图6可知，即使是在小时间尺度条件下，推移质颗粒均方位移曲线斜率均介于1和2之间，不符合均匀沙的小时间尺度“类弹道”扩散规律［2，11-12］。在本文非均匀沙试验中，不同颗粒的扩散特性存在一定差异，其中大颗粒均方位移随长时间尺度衰减较快，小颗粒均方位移随时间间隔衰减较慢。

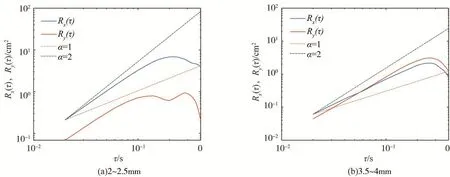
图5 不同粒径组颗粒均方位移随时间间隔变化

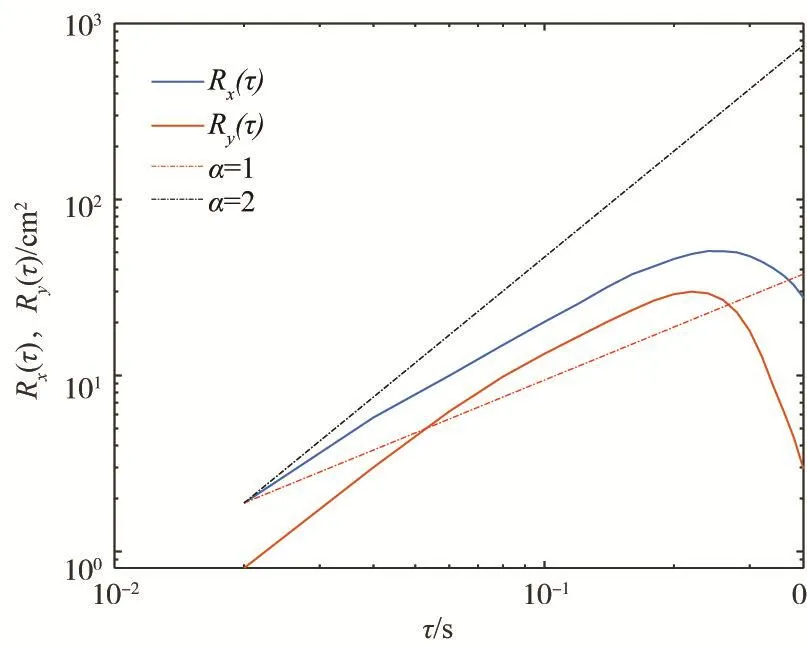
图6 所有颗粒均方位移随时间间隔变化

3.2 颗粒运动的速度自协方差 泥沙颗粒在运动时段Tp内的平均运动速度为uˉp，则颗粒运动速度与平均运动速度的差值为u′p=up(t)-，则速度的自协方差为［11-12］：

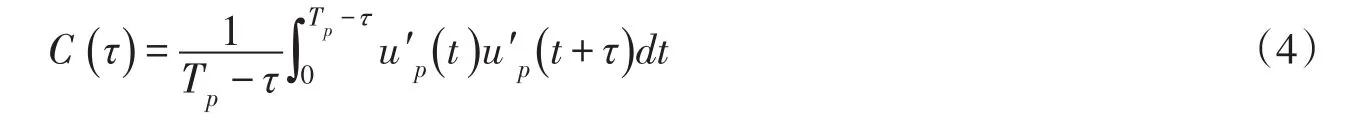
拉格朗日积分时间尺度可表示为：

τL表示流速的可持续性，如式（7）收敛，说明τL的值有限，则颗粒运动符合菲克扩散定律，且扩散规律满足下式：

当式（7）不收敛则表明颗粒运动表现为超扩散现象。

图7为按粒径分组的颗粒自相关系数随时间间隔的变化，可以看到，大多数颗粒运动的自相关系数均随时间呈衰减趋势，有部分颗粒在衰减过程中出现波动现象。与均匀沙成果相比，非均匀沙自相关系数衰减速率减缓，如在Furbish［2］、Fathel［11-12］的均匀沙试验中，颗粒运动x方向自相关系数在0.1～0.15 s左右衰减至接近0，y方向在0.1 s左右衰减至接近0。在本文非均匀沙试验中，衰减的时间间隔较长，衰减速率减缓，在时间间隔0.4 s左右时自相关系数还有0.2～0.3左右，且存在较为明显的波动现象。此外，粗化床面条件下x方向与y方向自相关系数随时间变化规律基本相同，如图7所示。

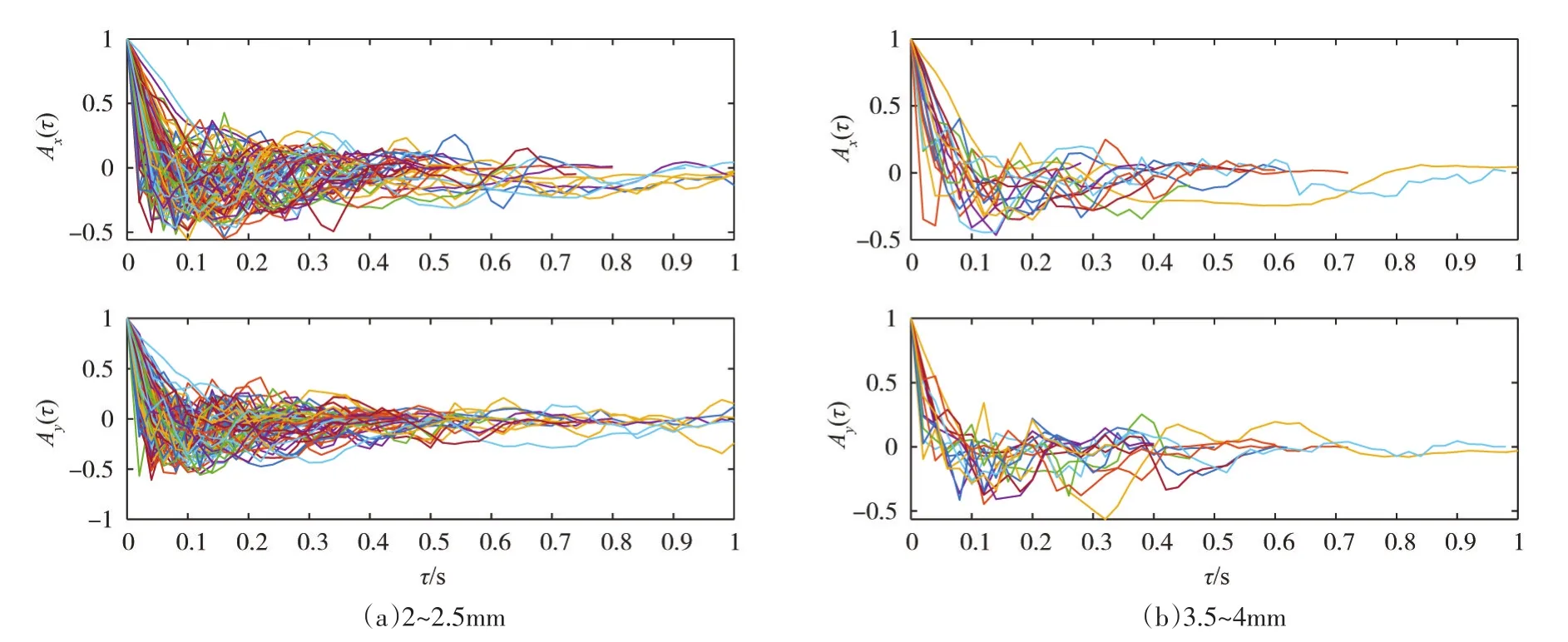
图7 按粒径分组的颗粒自相关系数随时间间隔的变化（图中：x表示水流方向，y表示横向方向）

3.3 非均匀沙扩散现象讨论 以上试验结果分析表明，粗化床面运动颗粒与均匀沙平整床面存在一定差异。对于均匀沙而言，颗粒大小均匀，在床面平整条件下，在水流作用下不同部位的泥沙颗粒被水流挟带的概率相等；假定被挟带走的颗粒为少量，挟带走的泥沙颗粒不会改变其他泥沙颗粒的受力条件；也就是说在平整床面均匀沙条件下，各颗粒受力条件类似，颗粒运动的状态基本不受其他颗粒的影响，床面当前的状态与历史无关，满足马尔科夫过程假定。而对于非均匀沙粗化床面，泥沙颗粒在水流作用下往往会形成不同的结构，粗化后的床面各处的结构不尽相同，当有泥沙颗粒被水流冲走，则该泥沙颗粒可能会改变当前的床面粗化结构形式，进而改变底部水流边界条件，反过来可能会对泥沙颗粒运动造成影响。

从床面随时间发展变化过程来看，均匀沙平整床面不同时刻均表现为平整形态，随时间变化不大。而对于粗化床面，某一时刻泥沙颗粒的冲离或停止有可能改变床面结构，造成粗化床面形态随时间发生变化，进而对后来的泥沙颗粒运动造成影响。因此，粗化床面条件下泥沙颗粒运动可能会对后续泥沙颗粒运动造成影响，表明泥沙颗粒的未来运动状态不仅与当前状态有关，也可能与颗粒运动的历史有关，非均匀沙床面泥沙运动可能难以满足马尔科夫过程所要求的无后效假定条件。

床面附近为水流紊动发展最为强烈的区域，也是流速梯度变化最大的区域。本文试验条件下，最大颗粒约20 mm，颗粒顶部床面与颗粒底部床面高差最大可达20 mm，位于顶部的水流流速远大于底部床面，同时各粗化结构体下游往往会形成较为强烈的尾流，从而形成远比平整床面复杂的底部水流条件。另一方面，推移质颗粒在跳跃运动过程中，运动速度与当地水流流速并不完全一致，因而颗粒在运动过程中会不断与水流进行着动量交换。均匀沙平整床面与非均匀粗化沙床面两种底部边界条件所形成的不同的水流条件，必然会造成颗粒与水流动量交换强度的不同。

布朗运动弹道扩散是指颗粒在液体分子与其两次碰撞之前的真空期，颗粒在此期间为不受任何作用力，仅在惯性作用下做自由运动，符合弹道扩散［23］；Fathel等［11-12］试验中均匀沙颗粒的“类弹道”运动，一方面可能是在小时间尺度下惯性占优，水流对颗粒的作用不明显，另一方面是由于泥沙颗粒运动速度较小，水流与泥沙颗粒动量交换不够充分。

图8为本文拍摄范围内实际床面，由图8可知，在非均匀沙粗化床面上存在着大量大小不一的粗化结构体，这些结构体会对局部水流运动造成一定影响，其中突起的结构体对水流和泥沙运动造成阻碍，形成减速作用；相互交错的结构在床面上可形成独立“通道”，泥沙颗粒在通过这些“通道”可能被加速，加速与减速同时存在，使粗化床面条件下的泥沙颗粒运动更易出现反常扩散现象［24］。图8中绘制了本文获取的所有颗粒的运动轨迹，可以清楚的看到几乎所有的颗粒均沿着几个相对固定的“通道”运动，仅有少部分颗粒可以摆脱“通道”的束缚，从粗化结构顶部跳跃而过。粗化床面上这种“通道”使泥沙颗粒运动不再是单一的x方向，而是随着通道内的水流运动方向运动，当颗粒刚好从与x方向具有一定夹角的通道内运动时，则会出现y方向具有类似于x方向的运动特征。基于试验结果和上述分析可知，粗化床面颗粒运动与天然河道观测到的反常扩散更为接近［8］，不符合均匀沙床面的“类弹道”扩散特性［2，11-12］。

图8 颗粒运动轨迹示意

4 结论与展望

推移质颗粒随机运动和扩散特性研究对于深入把握推移质规律，准确模拟推移质运动具有重要理论意义和实用价值，现阶段关于推移质颗粒扩散特性还存在一定分歧。已有研究多基于泥沙颗粒运动强度较小、床面处于大致平整阶段的均匀沙试验，虽有助于加深对不同条件下水沙相互作用机理的认识，但与天然河流存在较大差异。本文在大型水槽中开展了非均匀沙推移质试验，测量了粗化床面条件下的泥沙颗粒运动特性，以颗粒运动均方位移和自相关系数为参数，分析了粗化床面与平整均匀沙床面之间存在的差异，得到以下几点认识：

（1）粗化床面上的结构体改变了底部水流边界条件，对推移质泥沙运动造成较大影响，颗粒运动与扩散特性与均匀沙床面均存在一定差异。

（2）粗化床面上的非均匀沙在小时间尺度上未表现出均匀沙试验的“类弹道”扩散特性，受粗化结构影响，部分颗粒y方向运动强度与x方向运动强度在一个量级，甚至超过x方向运动。

（3）与均匀沙研究成果相比，非均匀沙两个方向的运动速度自相关系数衰减趋势变缓，衰减至零的时间由均匀沙的0.15 s变为非均匀沙的大于0.4 s，部分颗粒自相关系数存在一定波动，表明非均匀沙粗化床面条件下颗粒运动的记忆效应大于均匀沙平整床面。

（4）受粗化结构体影响，非均匀沙底部水流条件远比均匀沙平整床面复杂，泥沙颗粒在运动过程中与水流之间的动量交换强度与均匀沙存在差异，表现为颗粒运动扩散特征存在着较明显的反常扩散现象。

本文以高速摄像机拍摄的泥沙颗粒运动信息，分析了粗化床面条件下的泥沙颗粒扩散特性，并与均有沙床面试验进行对比。受试验和数据处理技术所限，本文分析所基于的拍摄时段较短，所获颗粒信息较少，未来随着图像处理技术发展，可对更长时间、更多颗粒运动进行分析。此外，本文仅从平面上识别了粗化床面所形成的二维“通道”，未来可基于数字图像处理技术获取粗化床面三维形态［25］，并将颗粒运动特性与床面三维形态相结合进行分析，进一步解析粗化床面对颗粒运动的定量影响。