基于K-Means算法的架空输电线路载流量计算

林锦荣 武云发 廖如超 陈郑淦哲

0 引言

载流量作为架空输电线路载流能力的重要标准,其取值的大小决定了架空输电线路动态增容的合理性,对电力调度和建设极为重要．边界条件是载流量计算过程中的重要参数,其取值是否合理决定了载流量计算结果的准确性[1-2]．

目前我国在架空输电线路载流量计算时,普遍使用的是《110 kV～750 kV架空输电线路设计规范》摩根公式[3]．同时,边界条件作为载流量计算的重要影响参数,目前我国载流量计算推荐的边界环境风速为0.5 m/s,环境温度为35 ℃．由于在载流量计算过程中使用的边界条件过于保守,导致无法充分发挥输电线路的载流量能力[4-5]．基于以上问题,文献[6]提出了一种载流量计算过程中边界条件的统计方法,通过传统的数学统计方法对气象数据进行统计并选定新的边界条件;文献[7]提出了一种气候条件对载流量影响的分析方法,得出对载流量有影响的因素由大到小依次为环境风速、环境温度以及日照强度．

随着人工智能时代的到来,统计机器学习方法被广泛应用于各个领域,成为人们不可或缺的数据分析手段[8]．其中,聚类算法在数据挖掘领域起着至关重要的作用,而在聚类算法中较为经典的算法有K-Means[9]、special clustering[10]等．其中K-Means由于其高效、易于实施的特点,到目前为止仍被广泛地应用于各个领域．

本文在传统的载流量计算方法的基础上,对载流量计算的边界条件进行重新选定．以广州地区近10年的气象数据为分析对象,对其进行筛选、预处理,根据各月气象数据的相似性,使用K-Means算法划分时段,并选取最为合适的边界条件进行载流量计算,通过实例分析验证本文提出的新方法的有效性[11]．本文的主要贡献如下:1)基于K-Means算法建立了时段划分与边界条件选定的数学模型;2)引入了极限边界条件载流量进行分析对比,通过安全裕度的计算解决了新选定边界条件下载流量计算结果的合理性问题．

1 气象数据分析

由于我国的地域辽阔,同一时间内由于经纬度的不同,气象条件差异较大．因此,非常有必要对特定地区的气象条件进行统计分析,得出该地区最为合适的边界条件．本文对广州地区2011—2019年的气象数据进行统计分析,主要统计的气象数据包括环境温度以及环境风速．

1.1 环境温度分析

环境温度的统计流程如下:

1)选取每日的最高气温作为统计对象,逐年统计出每个月的平均日最高气温(简称月平均气温)和每个月的最高气温(简称月最高气温):

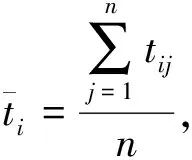
(1)

(2)

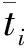
2)综合考虑多年来每个月的平均日最高气温和最高气温,计算出多年平均月平均气温、多年最高月平均气温、多年平均月最高气温、多年月最高气温:

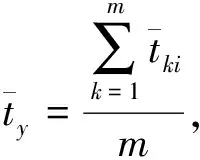
(3)

(4)

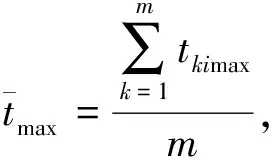
(5)

tymax=max{t1imax,t2imax,…,tmimax},

(6)

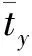
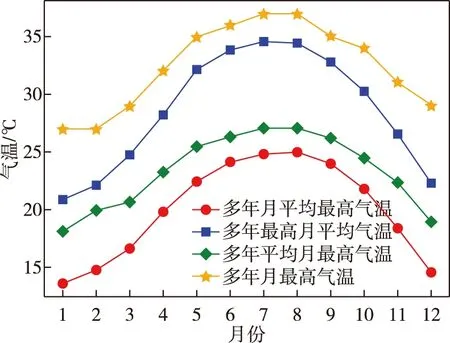
图1 广州地区近十年气温变化统计Fig.1 Monthly changes of temperature in Guangzhou in recent 10 years

1.2 环境风速分析

环境风速的统计流程如下:

1)选取每日的平均风速作为计算值,计算每个月平均风速:

(7)

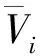
2)综合考虑多年来每个月的平均风速,计算出多年平均月平均风速、多年最高月平均风速、多年最低月平均风速:

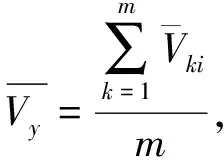
(8)

(9)

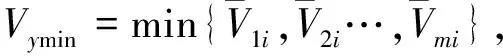
(10)

图2 广州地区近十年风速变化统计Fig.2 Monthly changes of wind speed in Guangzhou in recent 10 years

2 基于K-Means算法的气象聚类

K-Means算法是基于样本集合来划分的一种聚类算法．将12个月的气象数据看作一个数据集,共包含12个样本．通过K-Means算法确定簇k的个数,再将12个样本划分到k个簇中,使每个样本到所属簇的中心的距离最小[12]．

2.1 基于轮廓系数的k值确定

通过轮廓系数计算,确定最佳的划分簇k的值．单个样本的轮廓系数公式如下:

(11)

进一步可解析为

(12)

其中：a为样本与其自身所在的簇中的其他样本的相似度,等于样本与同一簇中所有其他点之间的平均距离;b为样本与其他簇中的样本相似度,等于样本与下一个最近的簇中所有点之间的距离．根据聚类算法遵循簇内样本差异尽可能小、簇外样本差异尽可能大的原则,由式(12)可知每个样本的轮廓系数的范围是(-1,1),且越接近1越好．因此,当选择不同的k值时,如果整个数据集的平均轮廓系数越接近1,则聚类效果越好,k的值越合适．

把一年12个月的数据看作一个数据集,进行轮廓系数计算,仿真结果(k=3)如图3所示．

图3 轮廓系数计算仿真结果(k=3)Fig.3 Simulation of contour coefficient calculation(k=3)

由仿真结果可知,当k的数值选择为3时,轮廓系数最接近1,效果最好．因此,广州地区一年12个月的气象条件划分为3个时段最为合适,分别命名为高温月份、低温月份和其他月份．

2.2 基于K-Means算法的气象聚类

对于一个簇来说,所有样本点到质心的距离之和越小,就可以认为这个簇中的样本越相似,簇内差异越小．使用K-Means算法将12个月份样本聚类到高温月份、低温月份和其他月份3个簇中．具体步骤如下:

步骤1.随机选择3个样本点作为簇的中心．t=0,簇中心集合为

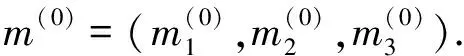
(13)

步骤2.计算每个样本点到簇中心的距离,将每个样本点派到与其最近的簇中．距离计算量度使用欧几里得距离:

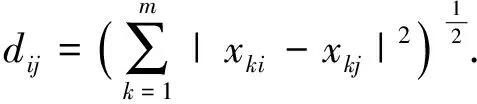
(14)

步骤3.计算各个簇的均值得到新的簇中心集合:

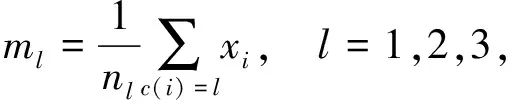
(15)

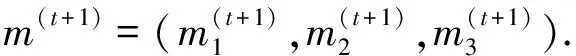
(16)

步骤4.重复步骤2、步骤3使目标函数达到收敛为止,输出每个样本所属的簇．目标函数如下式所示:

(17)

当目标函数收敛后,共包含3个簇,簇标签分别为高温月份、低温月份和其他月份．通过对每个样本点进行欧几里得距离计算,可得出每个样本到对应簇中心的距离,以及每个样本所属的簇标签．其中,高温月份包含5月、6月、7月、8月、9月共5个月份,低温月份包含12月、1月、2月、3月共4个月份，其他月份共包含4月、10月、11月共3个月份．其中每个簇的中心对应数值如表1所示．

因此,从表1数据可得,在高温月份时间段内最高温度为36 ℃,最低平均风速为0.86 m/s;在低温月份时间段内最高温度为28 ℃,最低平均风速为1.21 m/s;在其他月份时间段内最高温度为32.33 ℃,最低平均风速为1.09 m/s．由于以上边界条件的取值是根据簇样本中心的极限范围进行选取的,因此把上述边界条件定义为对应时段下可获取的极限边界条件．

表1 簇中心样本数据汇总

3 基于选定边界条件下的载流量计算

3.1 边界条件选定

在实际工程中,需要考虑一定的安全裕度以防止载流量设置过高而产生故障．在考虑一定安全裕度的情况下,高温月份时间段内,环境温度的边界值设置为40 ℃,环境风速的边界值设置为0.8 m/s;在低温月份时间段内,环境温度的边界值设置为30 ℃,环境风速的边界值设置为1.2 m/s;在其他月份时间段内,环境温度的边界值设置为35 ℃,环境风速的边界值设置为1.0 m/s．因此,在一定安全裕度情况下的环境温度和环境风速作为最终选定的边界条件．边界条件的对比如表2所示．

3.2 载流量计算

经过对广州地区气象数据的统计分析,并最终选定高温月份、低温月份以及其他月份对应环境温度以及环境风速的边界值．边界条件选定后,根据摩根公式进行载流量的计算[13-14]．

载流量计算选用我国标准DL/T 5092中的摩根公式[15]:

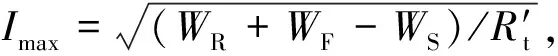
(18)

式中:Imax为输电线路载流量(A);WR为单位长度导线的辐射散热功率;WF为单位长度导线的对流散热功率;WS为单位长度导线的日照吸热功率;R′t为导线的交流电阻．

辐射散热功率WR的计算式:

WR=πDE1S1[(t+ta+273)4-(ta+273)4],

(19)

式中:D为导线外径;E1为导线表面的辐射散热系数,光亮的新线为0.23～0.43,旧线或涂黑色防腐剂的线为0.90～0.95;S1为斯特凡-包尔兹曼常数,为5.67×10-8;t为导线表面的平均温升,ta为环境温度．

对流散热功率WF的计算式:

WF=0.57πλftRe0.485,

(20)

式中:λf为导线表面空气层的传热系数,λf=2.42×10-2+7(ta+t/2)×10-5;Re为雷诺数,Re=VD/v,其中v=1.32×105+9.6(ta+t/2)×10-8,V为环境风速,v为导线表面空气层的运动黏度．

日照吸热功率WS:

WS=αsJsD,

(21)

式中:αs为导线表面的吸热系数,光亮的新线为0.35～0.46,旧线或涂黑色防腐剂的线为0.9～0.95;Js为日光对导线的日照强度,当天晴、日光直射导线时,可采用1 000 W/m2．

交流电阻R′t:

Rt=R20[1+α20(t-20)],

(22)

R′t=λamRt,

(23)

其中：α20为20 ℃时电阻温度系数；t为导线最大允许工作温度；R20为20 ℃时导线的直流电阻；λam为交直流电阻比．

4 仿真分析

根据广州地区最终选定的边界条件进行载流量计算,其中高温月份(5月、6月、7月、8月、9月)环境温度40 ℃、风速0.8 m/s;低温月份(12月、1月、2月、3月)环境温度30 ℃、风速1.2 m/s;其他月份(4月、10月、11月)环境温度取35 ℃、风速1.0 m/s．在选定的边界条件下计算所得载流量与原始载流量和极限边界条件下的载流量进行对比分析[16-18],结果如表3所示．

表3计算结果表明:相对于原始载流量,选定边界条件下的载流量在低温月份以及其他月份时间段内有明显的提升空间．同时,相对于极限边界条件载流量,能保留一定的安全裕度．以LGJ-630/45导线为例进行分析,不同时段下3种载流量的仿真对比如图4所示．

表2 边界条件对比分析

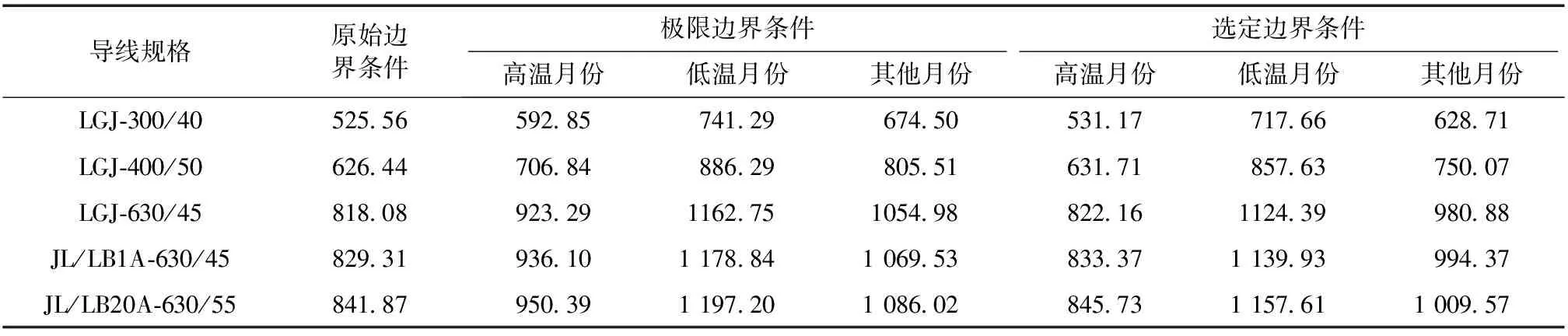
表3 载流量仿真计算对比

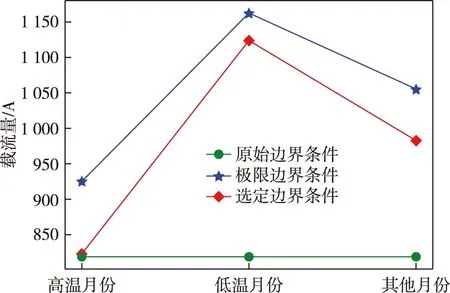
图4 导线LGJ-630/45载流量分析对比Fig.4 Current capacity comparison for conducting line LGJ-630/45 under 3 different temperatures

由图4并结合表3数据分析可得,相对于原始载流量,选定边界条件下，载流量在高温月份可提升0.50%,在低温月份可提升37.44%,在其他月份可提升19.90%．同时,与极限边界载流量对比分析可得,在高温月份可保留10.95%的安全裕度,在低温月份可保留3.30%的安全裕度,在其他月份可保留7.02%的安全裕度[19-20]．

5 结束语

本文在传统载流量计算方法的基础上,引入了K-Means算法，针对特定的地区将一年划分成不同时段,并根据每个时段的簇中心,选定新的边界条件．仿真分析验证了在新选定的边界条件下,在低温月份和其他月份两个时间段内可明显提升架空输电线路的载流量,同时可保留一定的安全裕度．

今后的工作将结合其他聚类算法,进一步考虑多种载流量计算影响因素下的最优组合问题．