考虑性能约束的航天器近距离悬停控制

张博翔 王理想 王辉 张彦鑫

0 引言

随着空间技术的不断进步，航天任务也逐渐向着复杂化与多样化的方向发展，诸如航天器在轨服务、空间碎片清理、小行星捕获等领域无论在理论研究还是实际应用中都具有较大挑战的概念和相关任务被提出，并受到越来越多的关注[1].而航天器的交会对接技术正是保证上述任务成功实现的关键性技术之一.航天器的交会对接是指两个航天器在空间中接近并且最终固连成为一体的过程[2].在交会对接的过程中，通常其中的一个航天器做被动飞行，被称为被动航天器或目标航天器，另一个航天器被控制做机动飞行，被称为主动航天器或追踪航天器[3-5].

交会对接技术是一项重要的空间技术，在许多航天任务中起到关键作用.它不仅仅是衡量一个国家航天技术发展水平的重要指标，作为一项空间技术，它更是一种拥有实用价值的手段[6].作为一种手段，交会对接技术在实际应用的过程中会受到各种限制，首先，在交会对接过程中，不仅对追踪航天器的轨道有要求，追踪航天器的姿态也同样要满足一定要求，此时航天器的轨道与姿态运动之间存在耦合并且不可忽略[7]，其次，在对追踪航天器控制的过程中，不仅需要关注追踪航天器到达指定状态时的控制精度，还需要考虑追踪航天器在到达指定状态过程中的瞬时状态、燃料消耗等指标[8-10].此外，在交会对接的最后阶段，两航天器之间非常接近，此时航天器的外形不可忽略，尤其当目标航天器为失效或故障航天器这一类非合作目标时，其可能伴随有自由翻滚等运动状态，若不考虑相应的避障设计，极有可能发生碰撞而导致整个任务的失败[11-12].因此，在考虑性能约束及轨迹安全的前提下，对航天器交会对接过程中的控制问题进行研究，可以满足新的航天任务的需求，无论在理论上还是工程应用上都有一定意义[13-16].

本文基于追踪航天器体坐标系下的相对姿轨耦合模型，对航天器交会对接中的悬停控制问题进行研究.考虑到所建立的相对姿轨耦合模型是一种非线性系统,首先基于线性滑模面设计了控制器.目前针对非线性系统的研究多关注于系统的稳态性能而忽略了系统在稳定过程中的瞬态性能，然而在大多数实际工程应用中，控制器作用下系统的瞬态性能也是不可忽略的.本文采用了预设性能控制方法以提高系统的瞬态性能，并结合滑模控制方法设计了控制器.考虑到实际应用中希望更短的控制时间，所以采用了一种新型的有限时间收敛的性能函数来限制系统的收敛时间.最后通过数值仿真验证各控制器的有效性，并对仿真结果进行对比和分析.

1 追踪航天器体坐标系下的相对姿轨耦合模型

采用修正的罗德里格参数(MPRs)描述的追踪航天器相对于目标航天器的姿态为

(1)

对应的姿态转移矩阵为

(2)

其中，S表示对应向量的叉乘矩阵,σe表示追踪航天器相对于目标航天器的姿态的修正罗德里格参数，σp表示追踪航天器姿态的修正罗德里格参数，σt表示目标航天器姿态的修正罗德里格参数.

设追踪航天器期望位置矢量在目标航天器体坐标系下为pf，如图1所示.

图1 相关矢量与坐标系Fig.1 Correlated vectors and coordinate system

追踪航天器在期望位置时,相对于惯性坐标系的位置和速度矢量在目标航天器体坐标系下为

rd=rt+pf，

(3)

(4)

其中，rt表示目标航天器相对于惯性坐标系的位置矢量，rd表示期望位置相对于惯性坐标系的位置矢量，ωt表示目标航天器旋转的角速度矢量.

在追踪航天器体坐标系下，追踪航天器相对于期望位置的相对位置矢量、相对速度矢量和相对角速度矢量分别为

re=rp-Perd，

(5)

ve=vp-Pevd，

(6)

ωe=ωp-Peωt，

(7)

其中，ωp表示追踪航天器旋转的角速度矢量.

(8)

其中，mp表示追踪航天器质量，fp和fpd分别为追踪航天器所受控制力和干扰力，τp和τpd分别为追踪航天器所受控制力矩和干扰力矩，Jp表示追踪航天器对其本体系的转动惯量.

ft和ftd分别为目标航天器所受控制力和干扰力，τt和τtd分别为目标航天器所受控制力矩和干扰力矩，Jt表示目标航天器对其本体系的转动惯量.

定义状态变量

整理式(8)得到追踪航天器体坐标系下相对姿轨耦合的误差模型为

(9)

其中

本文的设计目标是：已知追踪航天器期望位置矢量在目标航天器体坐标系下为pf，当pf为固定值时，针对相对姿轨耦合的误差模型(9)，若设计控制器使系统状态最终收敛至0，此时追踪航天器实现对目标航天器的悬停.

2 追踪航天器近距离悬停的滑模控制

假设1存在ζ>0使得追踪航天器所受干扰力与干扰力矩‖d‖<ζ.

选取滑模面：

s=ce1+e2，

(10)

其中c=diag(c1,c2,…,c6)为滑模面系数.

设计如下控制器：

(11)

V(t)+αVγ(t)≤0 ，

(12)

则系统在有限时间内收敛，且收敛时间满足：

医院医疗与教学是一个全过程的管理流程。如图1所示，流程主要包括“读取系统数据”、“初始化排课数据”、“初始计算工作强度”、“修改排课数据” 、“重新计算工作强度”、“上课提醒”。对流程中间的每一个环节都进行消息推送机制，达到对工作人员的全过程提醒机制，可以让工作人员及时获得相关推送信息，提高管理工作者的工作效率，减少教师迟到、早退、不备课等教学差错发生率。

(13)

定理1对于系统(9)，在控制器(11)作用下，系统状态量e1及e2可以渐近收敛到0.

证明首先证明滑模面上，即s=0，e1及e2渐近收敛到0.

当e1=0时，显然e2=0.当e1≠0时滑模面s=ce1+e2=0可知e2=-ce1.

选取Lyapunov函数

(14)

对其求导得：

(15)

(16)

然后证明在控制器(11)作用下，系统状态在有限时间内到达滑模面.

选取Lyapunov函数

(17)

对其求导，并将控制器(11)代入可得：

sT(C-1d-(‖C-1‖ζ+ε)sgn(s))≤

‖sT‖‖C-1‖ζ-‖sT‖‖C-1‖ζ-

(18)

由引理1可知系统状态在有限时间内抵达滑模面，定理得证.

3 考虑性能约束的滑模控制器设计

针对非线性系统的控制问题，目前的研究大多只关注系统的稳态性能而忽略了系统在稳定过程中的瞬态性能.预设性能控制是一种对系统瞬态性能和稳态性能同时进行约束的控制方法，其基本思想是通过人为设定某种包络(性能函数)对系统在收敛至稳态的过程中以及收敛至稳态时的状态误差进行限制.预设性能控制包含两个基本环节：性能函数和误差变换.

1)性能函数

对于性能函数ρ，应该具有如下性质：

①ρ恒为正且严格递减；

②ρ时间相关且连续可导.

可以看出满足条件的函数有无穷多个，常用的性能函数有以下两种：

ρ(t)=coth(l1t+l2)-1+ρ∞，

(19)

ρ(t)=(ρ0-ρ∞)e-αt+ρ∞.

(20)

本文选用(20)形式的性能函数，其中ρ=diag([ρ1ρ2…ρi])，i取决于误差e的维数，ρ0为性能函数初始值，ρ∞为最大容许的稳态误差，α为误差指数衰减速度.ρ0,ρ∞和α均为可设计参数，且满足ρ0>ρ∞>0，α>0.

给出如下不等式约束：

(21)

其中ei和ρi分别表示e和ρ的各个分量，t∈[0,∞)，δ∈[0,1].

如图2所示，当不等式约束(21)满足时，误差曲线将被限制在性能函数包围的区域中，即系统误差将收敛到±ρi,∞和±δρi,∞之内.

图2 不等式约束示意图(e(0)>0)Fig.2 Schematic diagram of inequality constraints (e(0)>0)

2)误差变换

由于引入了不等式约束(21)，使得控制器设计变得复杂.因此引入误差变换函数，将不等式约束转换为等价等式约束，再对之后的系统进行控制器设计.

定义误差变换：

e(t)=ρ(t)F(κ)，

(22)

其中κ为变换误差，为使误差变换后的等式约束与原不等式约束等价，F(κ)应该满足以下条件：

①F(κ)光滑可逆且严格递增；

②存在

(23)

本文采用如下变换函数：

(24)

对误差变换e(t)=ρ(t)F(κ)，有

(25)

以e(0)>0为例分析，当e(t)到达性能函数包围的边界，即e(t)=ρ(t)或e(t)=-δρ(t)时，此时有F(κ)=1或F(κ)=-δ，因此有κ→∞.若设计控制器，使得κ有界，原系统状态误差即可满足预设性能约束.

对于式(25),由于ρ(t)恒为正，当e(t)=0时，有F(κ)=0.对于式(24)，本文中取δi=1，则此时有：

(26)

若令F(κi)=0，有κi=0，若设计控制器使得κi=0，则原系统状态误差既可以满足预设性能约束，又可以稳定.

(27)

对其求导，有

(28)

令

(29)

则

(30)

将系统(9)代入式(30)中，可以得到变换后的系统为

(31)

考虑线性滑模控制，针对系统(31)，在满足假设1时,选取如下滑模面：

s=cκ1+κ2，

(32)

其中c=diag(c1,c2,…,c6)为滑模面系数.

设计如下控制器：

(33)

定理2在控制器(33)作用下，系统(31)渐近稳定，原系统(9)渐近稳定且满足性能约束条件.

证明选取如下的Lyapunov函数：

(34)

对其求导，并将控制器(33)代入可得：

sT(β2C-1d-(‖β2C-1‖ζ+ε)sgn(s))≤

‖sT‖‖β2C-1‖ζ-‖sT‖‖β2C-1‖ζ-εsTsgn(s)=

(35)

由引理1可知系统状态在有限时间内抵达滑模面，定理得证.

对于性能函数(20)，虽然可以限制系统的瞬态性能与稳态性能，但是不能保证系统在有限时间内收敛至ρ∞内.本文将采用一种新型性能函数，首先保证性能函数在有限时间内收敛，在性能函数约束下，转换后的系统状态也将在有限时间内收敛.

引理2若性能函数ρ(t)满足以下条件：

(36)

此时在ρ(t)的限制下，系统也将在有限时间内收敛至指定精度.

证明选取如下形式的Lyapunov函数：

(37)

对其求导有

(38)

由α∈(0.5,1)，有(α+1)/2∈(0.75,1).由引理1可知ρ(t)将限时间内收敛且收敛时间满足：

(39)

定理3在控制器(31)作用下，选用形式为(36)的性能函数，原系统(9)满足性能约束条件且在有限时间内收敛.

定理3证明同定理2.

4 仿真分析

追踪航天器轨道参数为：轨道半长轴a=6 800 km，轨道偏心率e=0.1，轨道倾角i=51.8°，升交点经度Ω=70.4°，近心点角距ω=46.5°，真近点角θ=8.2°.在惯性坐标系下，追踪航天器初始位置为[-1.905 8,4.819 5,4.339 2]T×106m，初始速度为[-4.7,-5,-3.5]T×103m/s.其他仿真参数如表1所示.

表1 仿真参数

4.1 滑模控制器仿真

选取滑模面系数c=diag([0.01,0.01,0.01,0.1,0.1,0.1])，为减小到达滑模面后的抖振现象，将控制器中的符号函数替代为饱和函数.

仿真结果如图3—8所示.

图3 相对位置误差Fig.3 Relative position errors under sliding mode controller (11)

图4 相对姿态误差Fig.4 Relative attitude errors under sliding mode controller (11)

图5 相对速度误差Fig.5 Relative speed errors under sliding mode controller (11)

图6 相对角速度误差 Fig.6 Relative angular velocity errors under controller (11)

图7 控制力曲线Fig.7 Control force curves under controller (11)

图8 控制力矩曲线Fig.8 Control torque curves under controller (11)

从仿真结果可知，采用控制器(11)时，系统的状态最终收敛至平衡点，此时追踪航天器到达期望位置.从中也可看出，系统的控制时间较长，收敛较慢，而且系统的瞬态性能较差，尤其是相对位置误差具有较大的超调量.

4.2 考虑性能约束的滑模控制器仿真

仿真初始参数与表1相同，滑模面系数c=diag(1,1,1,1,1,1)，分别选取形式如下的性能函数ρ1(t)=(40-0.01)e-0.01t+0.01，ρ2(t)=(1.5-0.01)e-0.01t+0.01，ρ3(t)=(1-0.01)e-0.01t+0.01，ρ4(t)=(0.05-0.01)e-0.01t+0.01.

对相对位置误差、相对姿态误差、相对速度误差和相对角速度误差进行约束.将控制器中的符号函数替代为饱和函数.

仿真结果如图9—14所示.

图9 相对位置误差Fig.9 Relative position errors under controller with prescribed performance

图10 相对姿态误差Fig.10 Relative attitude errors under controller with prescribed performance

图11 相对速度误差Fig.11 Relative speed errors under controller with prescribed performance

图12 相对角速度误差Fig.12 Relative angular velocity errors under controller with prescribed performance

图13 控制力曲线Fig.13 Control force curves under controller with prescribed performance

图14 控制力矩曲线Fig.14 Control torque curves under controller with prescribed performance

从上述仿真结果可以看出，与控制器(11)相比，通过结合了预设性能控制方法之后，对系统状态的瞬态性能做了较大的优化，以X轴相对位置误差为例，如图15所示，可以明显看出相对位置误差的超调量下降了很多.除此之外，系统收敛速度有所增加，这是由于性能函数本身的衰减速度加快了系统状态的收敛速度.总体来看结合了预设性能方法的滑模控制收敛时间更快且有更好的瞬态性能.需要注意的是，性能函数的参数选取需要合理，性能函数中的α为误差指数衰减速度，当其过大时，性能函数衰减速度过快会导致控制器控制力陡然增加而最终失控.

图15 X轴相对位置误差对比Fig.15 Comparison of relative position error at X axis

4.3 采用新型性能函数的控制器仿真

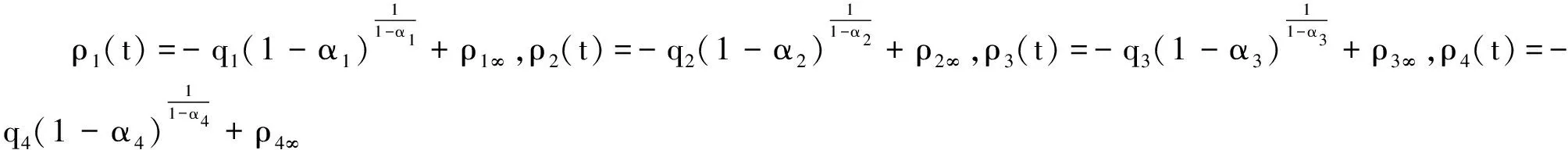
图16 相对位置误差Fig.16 Relative position errors under controller with new performance function

图17 相对姿态误差Fig.17 Relative attitude errors under controller with new performance function

从仿真结果可以看出，通过选取新型性能函数，系统的收敛速度快于滑模控制器和采用普通性能函数的控制器.选取相同的收敛精度时，三种控制器的具体收敛时间如表2所示.

图18 相对速度误差Fig.18 Relative speed errors under controller with new performance function

图19 相对角速度误差Fig.19 Relative angular velocity errors under controller with new performance function

图20 控制力曲线Fig.20 Control force curves under controller with new performance function

图21 控制力矩曲线Fig.21 Control torque curves under controller with new performance function

表2 收敛时间

5 结论

本文研究了性能约束下航天器的近距离悬停控制问题.首先针对追踪航天器体坐标系下的相对姿轨耦合模型，设计了滑模控制器，并基于李雅普诺夫稳定性原理进行了稳定性分析.其次，为提高系统的瞬态性能，结合滑模控制设计了相应的控制器，并基于李雅普诺夫稳定性原理进行了稳定性分析.考虑到有限时间控制问题，采用了一种新型的性能函数使系统在有限时间内稳定.最后通过数值仿真验证了控制器的有效性.