螺旋槽小孔节流动静压气体轴承静态特性研究*

王欣崎 李 博 李树森 贾 勇

(东北林业大学机电工程学院 黑龙江哈尔滨 150040)

近期研究表明，动静压气体轴承能有效避免启停阶段的干摩擦现象，增强轴承承载能力，满足主轴启停阶段的支撑刚度，提高主轴旋转的稳定性[6-8]。有学者提出通过开设动压槽与不同节流方式相结合来提高轴承的承载能力和稳定性。贾晨辉等[9]建立球面螺旋槽动静压气体轴承模型，利用6DOF被动型网格模拟分析轴承在不同转速下的运动状态。陈坚[10]分析气浮轴承螺旋槽结构参数变化对动静态特性的影响。王广洲等[11]以人字槽狭缝节流动静压气体轴承为研究对象，研究偏心率、转速及狭缝类型、人字槽数、狭缝数等参数对轴承静态性能的影响。李树森和潘春阳[12]研究具有深浅腔小孔节流动静压气体轴承在不同偏心率和转速情况下的气膜流场压力分布。张广辉[13]结合非线性动力学理论和方法，通过数值仿真和试验手段研究高速动静压混合气体轴承转子系统的动力学特性。

基于以上研究，本文作者设计一种螺旋槽小孔节流动静压气体轴承，综合螺旋槽能够产生动压效应以及小孔节流器承载能力大、刚度高等优点[14-15]，并利用Fluent对螺旋槽小孔节流动静压气体轴承静态特性进行研究，为提高气体轴承承载能力和刚度提供理论基础。

1 轴承结构和工作原理

图1所示为螺旋槽小孔节流动静压气体轴承结构示意图。轴承体上同时加工有小孔节流器和螺旋槽，轴承体外侧壁采用双排供气孔，每排供气孔为8个，且每个供气孔底部与小孔节流器连接。轴承体内侧壁沿圆周方向开设有8条矩形轴向微通槽，使得双排节流孔相通，开设的12对螺旋槽对称分布于微通槽两侧。

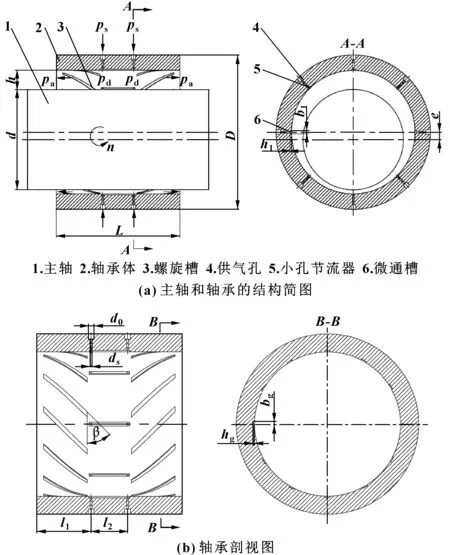
图1 螺旋槽小孔节流动静压气体轴承结构示意Fig1 Schematic of spiral groove small orifice throttle hybrid gas bearing structure (a) structure diagram of main shaft and bearing；(b) bearing cross-sectional view

图1中：ps为供气压力；pa为环境压力；pd为节流末端压力；d为主轴直径；n为主轴转速；e为偏心量；h为气膜厚度；D为轴承外径；L为轴承长度；l1为孔边距；l2为孔间距；ds为节流孔直径；d0为供气孔直径；β为螺旋角；bg为螺旋槽宽度；hg为螺旋槽深度；b1为微通槽宽度；h1为微通槽深度。微通槽的设计能够实现均化压力的作用，但要避免由于气膜内气体体积增大而使轴承产生气锤自激振动的现象，因此其尺寸的选择应满足b1=(2～3)ds；h1=(5～10)h0,其中h0为平均气膜厚度。初步确定主轴和轴承的结构参数和工作参数如表1所示。

表1 主轴和轴承的结构参数和工作参数Table 1 Structure and working parameters of main shaft and bearing

工作时，因载荷作用主轴与轴承之间形成偏心结构，致使气膜厚度分布不均而产生压力差，将主轴浮起。在开始阶段，具有压力的气体从供气孔被导入到小孔节流器中，通过小孔节流器孔喉部截面的节流作用后进入气膜间隙，形成静压承载。当主轴高速运转时停止外部高压供气，利用轴颈的回转将轴承间隙内的黏性气体带入轴承自身的螺旋槽中，此时主要靠螺旋槽的动压效应工作，形成动压承载。

2 计算模型建立与边界条件设计

2.1 计算模型的建立

利用三维建模软件SolidWorks建立螺旋槽小孔节流动静压气体轴承的气膜模型，如图2所示。

图2 螺旋槽小孔节流动静压气体轴承的三维气膜模型Fig 2 Three-dimensional gas film model of spiral groove small orifice throttle hybrid gas bearing

2.2 网格划分

利用Gambit软件对轴承的气膜模型进行网格划分，如图3所示。由于气膜模型的气膜厚度相对其他尺寸小很多，导致网格元素纵横比较大，无法进行一体化网格划分，因此采用结构化和非结构化的混合网格，以提高计算精度和速度。

图3 气膜模型的网格划分示意Fig 3 Schematic of the mesh division of gas film model (a) integral gas film grid;(b) grid at the orifice;(c) grid at the spiral groove

2.3 假设条件及边界条件的确定

为了方便计算求解，假设润滑介质是理想气体且为等温层流，气体黏性系数为常数；并假设轴承表面为刚性，轴承稳态运动，气体在气膜间隙中不存在相对滑动；忽略沿气膜方向的压力变化、轴承表面的曲率以及流体的惯性力。则可通过求解动静压气体轴承的雷诺方程[16](1)得到气膜的压力分布。

(1)

式中：p为压力函数；ρ为流量密度；v为平均流速；h为气膜厚度；pa为环境压力；ρa为环境密度；μ为气体动力黏度；vx、vz为气流速度分量。

引入量纲一化参数，取p0、hm、L为参考量，可得到量纲一化雷诺方程：

(2)

(3)

对于简化后的雷诺方程，设置其边界条件如下：

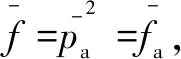
3 计算求解

(4)

通过对压力方程的计算获得压方值后，可求得每一单元体的承载能力Wλ，进而可以通过式(5)对所有单元体累加求和得到气体轴承的总承载能力W。

(5)

式中：W为气体轴承总承载能力；Wλ为每个有限单元体的承载能力；λ为第λ个单元体；n为有限单元体个数。

气膜刚度K是抵抗承载能力变化的能力，可由方程(6)来计算。

(6)

式中：ΔW为承载能力的变化量；Δe为对应的偏心变化量。

4 仿真结果与分析

4.1 不同供气压力下偏心率对轴承静态特性的影响

保持其他参数不变，选取供气压力分别为0.4、0.5、0.6、0.7、0.8 MPa，分析随偏心率从0.1增大到0.8的过程中轴承承载能力及刚度的变化规律，结果如图4、5所示。

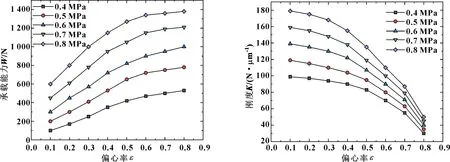
图4 偏心率与承载能力关系曲线 图5 偏心率与刚度关系曲线Fig 4 Relationship curves between eccentricity and bearing capacity Fig 5 Relationship curves between eccentricity and the stiffness

由图4和图5可知，在同一偏心率下，供气压力对承载能力和刚度的影响趋势相同，供气压力增大，使得气膜压力也增大，则承载能力和刚度随之上升;供气压力相同时，轴承的承载能力随偏心率的增大而增大，偏心率从0.1增大到0.6的过程中，承载能力增长迅速，而偏心率大于0.6以后承载能力增速缓慢；轴承的刚度则随偏心率的增大而减小，偏心率小于0.4时，刚度缓慢减小，偏心率大于0.4后刚度减小的速度不断增加。上述结果表明，偏心率过小无法满足轴承高承载能力的要求，而偏心率过大又无法满足轴承高刚度的要求。

4.2 不同转速下螺旋槽对轴承静态特性的影响

为了准确对比有、无螺旋槽对轴承静态特性的影响，建立无螺旋槽小孔节流动静压气体轴承模型与文中模型进行比较，并保持其他参数不变，研究转速对承载能力和刚度的影响规律，如图6、7所示。

图6 转速与承载能力关系曲线 图7 转速与刚度关系曲线Fig 6 Relationship curves between speed and bearing capacity Fig 7 Relationship curves between speed and stiffness

由图6和图7可知，同一转速下，有螺旋槽模型的承载能力和刚度都较无螺旋槽模型显著提高，且随转速的提高两模型之间的差值越来越大，这是因为螺旋槽对轴承的动压效应随转速的提高而增强。

4.3 不同节流孔直径下螺旋槽尺寸对气体轴承静态特性的影响

开设螺旋槽可提高轴承静态特性，但螺旋槽结构参数变化时也会对轴承静态特性产生影响。在节流孔直径为0.2、0.3、0.4、0.5、0.6 mm时，分别研究螺旋槽不同宽度和深度对轴承静态特性的影响。

螺旋槽宽度变化会导致有槽部分的面积变化，先固定其他参数，改变螺旋槽宽度，得到承载能力和刚度变化曲线，如图8、9所示。

图8 螺旋槽宽度与承载能力关系曲线Fig 8 The relationship curves between the width of the spiral groove and the bearing capacity

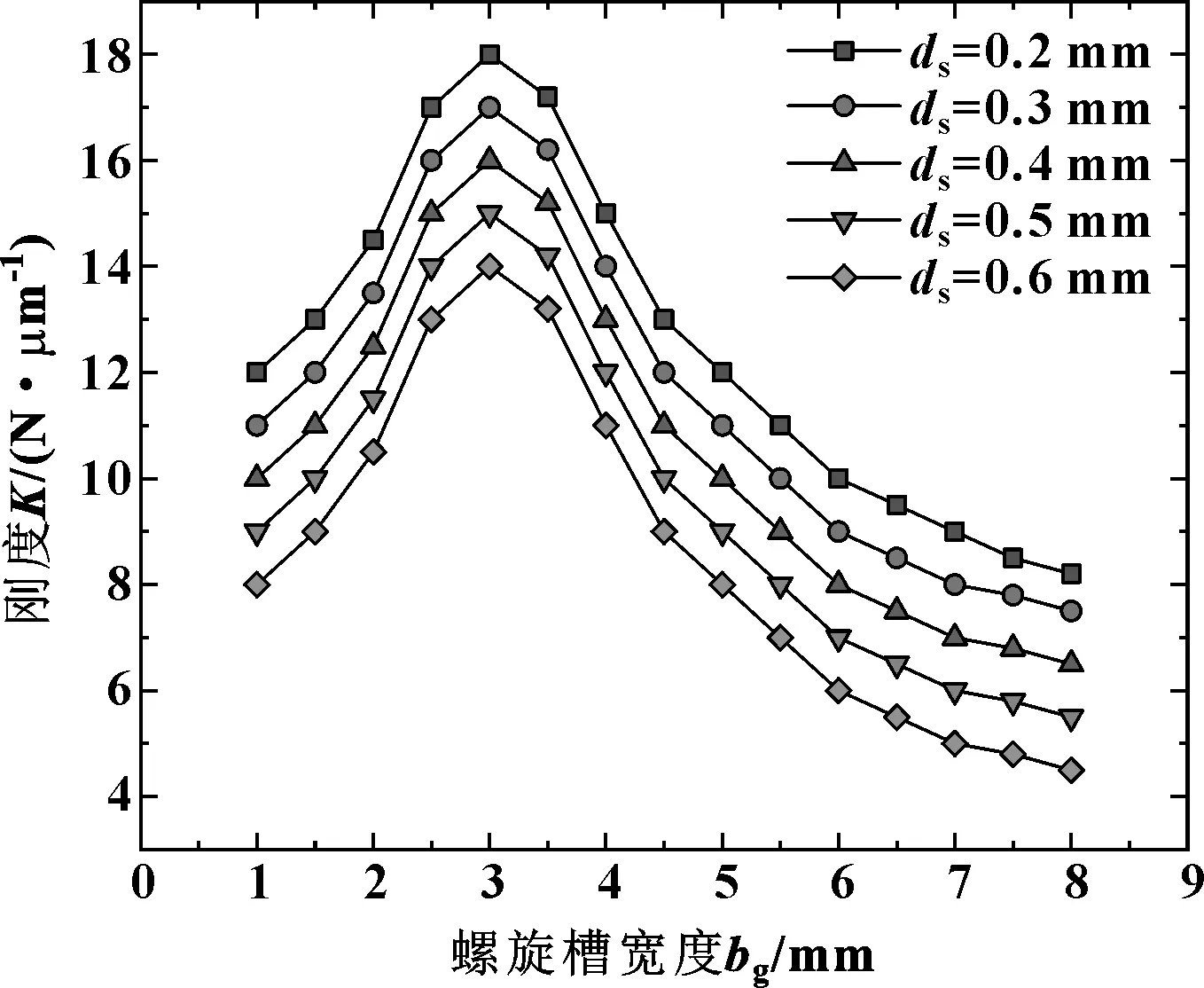
图9 螺旋槽宽度与刚度关系曲线Fig 9 The relationship curves between the width of the spiral groove and the stiffness

由图8和图9可知，轴承的承载能力以及刚度均先随螺旋槽宽度的增加而增大，存在一个极大值，而后呈减小趋势，并且二者下降的速度越来越小。这是因为当螺旋槽宽度bg≤3 mm时，随螺旋槽宽度的增加螺旋槽产生的动压效应不断提升。但当宽度bg>3 mm后气膜厚度明显增大，气膜压力减小，导致轴承静态特性下降;当宽度bg增大到5 mm后，压力下降值之差逐步减小，承载能力和刚度的变化也就逐步趋于稳定。同一宽度下，节流孔直径越小，承载能力越大，刚度越高。但是节流孔尺寸太小，容易产生小孔堵塞问题。

螺旋槽深度也是影响轴承静态特性的一个重要因素，改变螺旋槽深度，进行仿真分析的结果如图10、11所示。

图10 螺旋槽深度与承载能力关系曲线Fig 10 The relationship curves between the depth of the spiral groove and the bearing capacity

图11 螺旋槽深度与刚度关系曲线Fig 11 The relationship curves between the depth of the spiral groove and the stiffness

由图10和图11可知，螺旋槽深度相同时，节流孔直径越大，承载能力和刚度越小;随螺旋槽深度的增加，轴承的承载能力和刚度都呈下降趋势。在螺旋槽深度hg≤0.1 mm时，承载能力随槽深度缓慢下降，而当hg>0.1 mm时承载能力快速下降；而刚度随深度加深先呈快速下降趋势，在深度hg≤0.1 mm时快速下降，而深度hg>0.1 mm后下降速度平缓。上述结果表明，螺旋槽深度越小，越有利于提高轴承的承载能力和刚度，但是深度过小在给制造带来困难的同时也会影响轴承的稳定性。

4.4 仿真结果验证

为验证仿真结果的正确性，利用仿真方法对验证模型进行仿真计算，验证模型参数如表2所示。将仿真结果与理论求解结果进行对比，如图12所示。可知仿真结果与理论求解结果具有很好的一致性，只存在微小差异，表明文中的仿真结果是可信的。

表2 验证模型参数Table 2 Verification model parameters

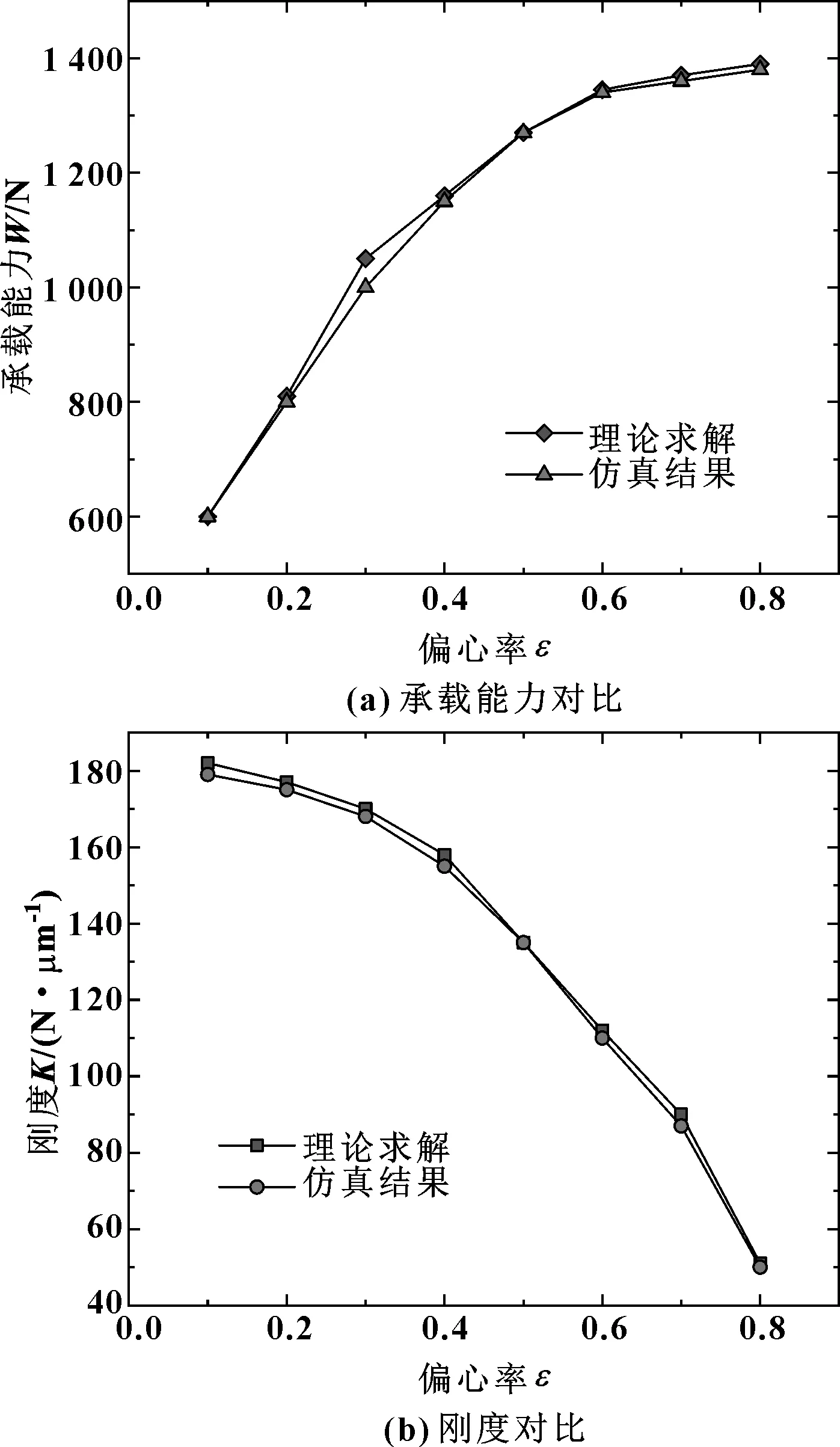
图12 理论求解与仿真结果对比Fig 12 Comparison of theoretical solution and simulation results(a) comparison of carrying capacity;(b) comparison of stiffness

5 结论

对螺旋槽小孔节流动静压气体轴承静态特性进行仿真分析，研究其结构参数和工作参数对轴承静态特性的影响规律，结论如下：

(1)相同偏心率下，随供气压力的升高，轴承静态特性增强；相同供气压力下，承载能力随偏心率的增大而增大，而刚度随偏心率的增大而减小。

(2)螺旋槽能够显著提高轴承静态特性，且转速越大，螺旋槽对轴承的动压效应越好。

(3)保证其他结构参数不变时，轴承静态特性随螺旋槽宽度的增加先增大后减小，螺旋槽深度和节流孔直径越小越有利，但尺寸过小会导致制造困难。