圆柱滚子式三叉杆万向联轴器热弹流脂润滑特性分析*
杨福芹 肖乾浩 胡德兴 宋豪杰 刘 欣
(青岛科技大学机电工程学院 山东青岛 266061)
三叉杆联轴器[1]内部传递元件与滑道之间存在较大作用力,运动中接触区温度升高,使得润滑脂物理、化学性质改变,严重时润滑油膜破裂失效,产生胶合、磨损等缺陷[2-3]。因此研究联轴器的热弹流脂润滑特性对提高工作寿命、改善润滑状况具有重要的意义。ZHOU等[4]对滑动销杆带有环形凸起的三叉杆联轴器抗磨损结构进行了热弹流脂润滑特性研究;陈佳[5]对滑块槽安装滚珠轴承的三叉杆联轴器建立起点接触热弹流脂润滑数值分析模型,分析了运动参数和润滑脂性能参数对联轴器润滑特性的影响;赵顺[6]对具有织构化抗磨损结构的三叉杆万向联轴器进行了热弹流脂润滑特性分析,探究了织构化模型的冠状区宽度对润滑油膜压力、膜厚、平均温升的影响。
圆柱滚子式三叉杆联轴器[7]是一种新型万向联轴器,其滑块上嵌有多个滚子,与滑块槽之间形成线接触高副。本文作者对圆柱滚子式三叉杆万向联轴器建立起线接触弹流脂润滑数值分析模型,结合联轴器的实际稳态工况,分析考虑热效应后的联轴器润滑特性。
1 数值模型的建立与求解
1.1 圆柱滚子式三叉杆万向联轴器的几何模型
圆柱滚子式三叉杆万向联轴器由输入轴、滑块组件、三叉杆组件、输出轴组成,其中摩擦磨损最严重的区域是滑块与滑块槽接触区。文中根据圆柱滚子、滑块槽接触区特点,将二者的接触看作是无限长滚子与平面的线接触问题,研究啮合过程中联轴器轴线夹角、圆柱滚子半径、回转半径、润滑脂初始黏度以及流变指数对润滑油膜压力、膜厚和平均温升的影响。圆柱滚子式三叉杆万向联轴器及滑块组件结构如图1所示。

图1 圆柱滚子式三叉杆万向联轴器结构及滑块组件结构Fig 1 The structure of tripod universal coupling of cylindrical roller (a) and the structure slide block assembly (b)
1.2 基本方程
对于圆柱滚子式三叉杆万向联轴器,前期建立了等温数值分析模型,并采用LFTVer3.0弹流润滑油膜测量仪,利用双色光干涉技术进行了实验验证[8]。文中在此基础上,加入能量方程、热界面方程以及考虑温度作用的黏压方程、密压方程,进一步考察联轴器失效部位配合表面的热弹流脂润滑特性。
(1)脂润滑量纲一化Reynolds方程
基于Ostwald模型的一维量纲一化Reynolds方程[9-10]为
(1)
各量纲一化参数定义如下:
式中:P为量纲一油膜压力,P=p/pH,pH为最大Hertz压力,Pa;p为油膜压力,Pa;X为量纲一坐标,X=x/b;b为Hertz接触区半宽,μm;x为卷吸速度方向标量;H为量纲一膜厚,H=hR/b2;R为等效曲率半径,mm;E为当量弹性模量,Pa;n为流变指数;η*为量纲一润滑脂黏度,η*=η/η0;η为
润滑脂黏度,Pa·s;η0为环境温度下的润滑脂黏度,Pa·s;h为膜厚,m;U为卷吸速度,m/s。
Reynolds方程边界条件为
入口区:P(Xin)=0
出口区:P(Xout)=0,dP(Xout)/dX=0
(2)量纲一化膜厚方程
H(X)=H0+X2/2-
(2)
式中:H0为量纲一中心膜厚。
(3)量纲一化热弹流黏压黏温方程[11]
η*=exp{(lnη0+9.67)[(1+5.1×10-9p)0.68×
(3)
式中:T为润滑油膜温度;T0为环境温度。
(4)量纲一化热弹流密压密温方程[11]
(4)
式中:ρ*为量纲一润滑脂密度,ρ*=ρ/ρ0,ρ为润滑脂密度,kg/m3;ρ0为环境温度下的润滑脂密度,kg/m3;密温系数D=-0.000 65 K-1。
(5)量纲一化载荷方程
(5)
(6)量纲一化能量方程
润滑油膜的量纲一化能量方程[12-13]为
(6)
式中:T*为量纲一温度,T*=T/T0;u*为量纲一速度,u*=η0U/(2ER);c为润滑脂比热容,J/(kg·K)。
上、下接触面的温度边界条件为
(7)
(8)
式中:ρ1、ρ2分别为上、下表面材料密度,kg/m3;c1、c2分别为上、下表面材料比热容,J/(kg·K);k、k1、k2分别为润滑脂及上、下表面的传热系数,W/(m·K);s为滑滚比;u1、u2分别为上、下两表面切向速度,m/s。
1.3 数值计算
采用多重网格法求解Reynolds方程,采用多重网格积分法对膜厚求解,得到各个节点的弹性变形[14],采用步进法求解能量方程,采用逐列扫描法求解润滑油膜温度[15]。压力、温度的周期性相对收敛精度判断准则为
(9)
(10)
式中:k+1为当前循环,上标k为前一次循环,下标k为膜厚方向节点。
数值计算流程如图2所示。

图2 数值计算流程Fig 2 The flow of numerical calculation
2 结果与分析
初始参数设置为:X方向节点数129,膜厚Z方向节点数5,X起点坐标Xin=-4.0,Xout=1.4,R=5 mm,E=227 GPa,T0=298 K,c=2 000 J/(kg·K),c1=c2=470 J/(kg·K),k=0.14 W/(m·K),k1=k2=46 W/(m·K),ρ1=ρ2=7 850 kg/m3,s=0.8。润滑剂选择长城MP-3润滑脂,在温度298 K下:η0=0.1 Pa·s,ρ0=890 kg/m3,n=0.85。
2.1 几何参数对联轴器润滑特性的影响
由文献[16]可知,圆柱滚子式三叉杆万向联轴器的实际运动状况。滑块相对于滑块槽的位移h1的表达式为
h1=[R-R(1/cosβ-1)/2-R(1/cosβ-1)·
cos(2ωit)]cos(ωit)sinβ+R(1/cosβ-1)·
cos(3ωit)sinβ/2
(11)
式(11)两侧同时对时间t求导,得到滑块相对于滑块槽的速度v1的表达式为
v1=2R(1/cosβ-1)ωicos(ωit)sin(2ωit)sinβ-
3R(1/cosβ-1)ωicos(3ωit)sinβ/2-ωisin(ωit)sinβ·
[R-R(1/cosβ-1)/2-R(1/cosβ-1)cos(2ωit)]
(12)
2.1.1 输入轴与输出轴轴线夹角对联轴器润滑特性的影响
研究表明,输入轴滑块槽与圆柱滚子之间的相对速度随输入轴与输出轴的轴线夹角的增大而增大[8],因此,输入轴与输出轴的轴线夹角主要通过影响配合表面的相对速度来影响卷吸速度,进而影响联轴器的润滑特性。根据设定参数,其他条件不变,载荷w=9 kN/m,轴线夹角分别取β=2°、β=4°、β=6°时,对润滑油膜压力、膜厚和平均温升的影响如图3所示。
从图3(a)可以看出,3种轴线夹角下压力曲线表现出较好的一致性,油膜中心压力处变化曲线重合,随着轴线夹角的增大,二次压力峰明显升高。从图3(b)可以看出,随着轴线夹角的增大,膜厚呈现均匀增大的趋势。从图3(c)可以看出,轴线夹角增大,平均温升显著增加,温度峰向入口移动且愈加尖锐。
轴线夹角对润滑油膜的影响主要集中在峰值区域。轴线夹角增大时,带动运动振幅增大,使更多润滑脂进入接触区,增大了膜厚。二次压力峰、最小膜厚向入口方向移动,Hertz接触区变窄。随卷吸速度的增大,剪切运动强度加大,释放大量热量,提高了平均温升。

图3 轴线夹角对联轴器润滑特性的影响Fig 3 Effect of the angle between two shafts on lubrication characteristics of coupling (a) comparison of pressure; (b) comparison of film thickness;(c) comparison of average temperature
2.1.2 圆柱滚子半径对联轴器润滑特性的影响
圆柱滚子半径通过影响当量接触半径来影响联轴器润滑特性。根据设定参数,其他条件不变,平均速度U=0.1 m/s,载荷w=9 kN/m,圆柱滚子半径分别取R=0.003 m、R=0.004 m及R=0.005 m时,对润滑油膜压力、膜厚和平均温升的影响如图4所示。
从图4(a)可以看出,圆柱滚子半径增大,润滑油膜压力减小,中心压力与二次压力峰的差值减小。从图4(b)可以看出,润滑油膜厚度随圆柱滚子半径的增大而增大,且中心膜厚的变化要大于最小膜厚处,二者膜厚差值逐渐增大。从图4(c)可以看出,圆柱滚子半径对润滑油膜平均温升的影响显著。圆柱滚子半径增大,平均温升显著减小,温度峰越平缓。
圆柱滚子半径对润滑油膜的影响主要集中在油膜中心位置。Hertz接触区随圆柱滚子半径的增大而增大,使得承压面积扩大,油膜压力降低,膜厚增加,接触区内热积聚能力减弱,故平均温升降低。二次压力峰、最小膜厚以及温度峰位置变化不明显。
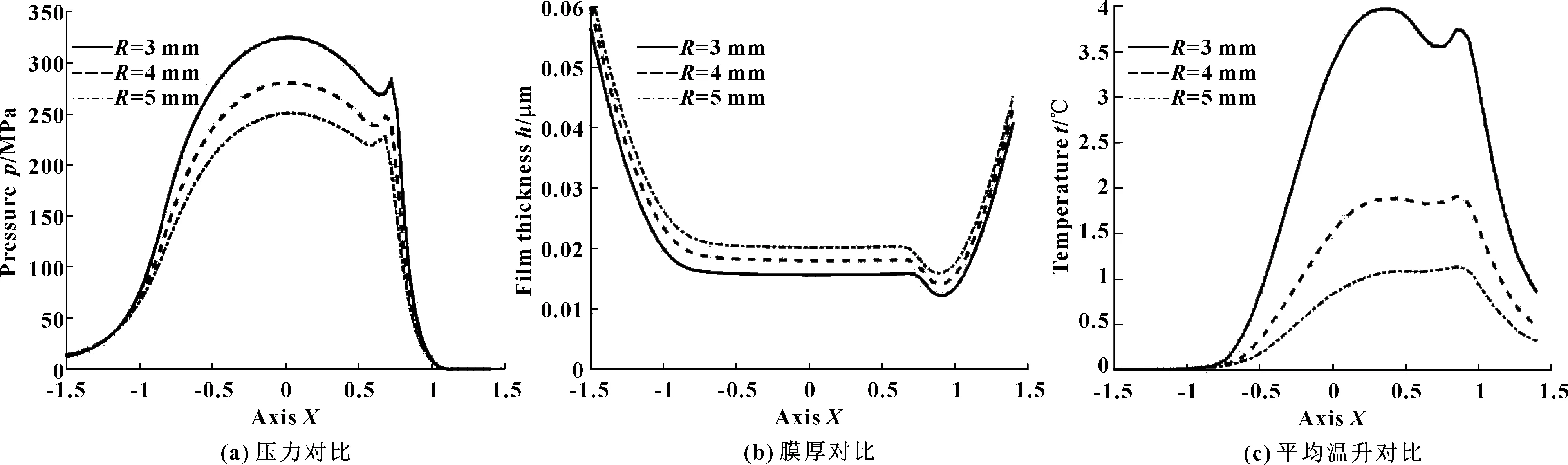
图4 圆柱滚子半径对联轴器润滑特性的影响Fig 4 Effect of the cylindrical roller radius on lubrication characteristics of coupling (a) comparison of pressure; (b) comparison of film thickness;(c) comparison of average temperature
2.1.3 输入轴回转半径对联轴器润滑特性的影响
研究表明,输入轴滑块槽与圆柱滚子之间的相对速度和作用力均随回转半径的增大而增大[8],因此,输入轴滑块槽回转半径会影响到圆柱滚子所受载荷和卷吸速度,进而影响联轴器的润滑特性。根据所设定参数,其他条件不变,回转半径分别取R1=0.03 m、R1=0.04 m和R1=0.05 m,相对应载荷分别取w=9 kN/m、w=19 kN/m和w=29 kN/m,卷吸速度分别取U=0.105 m/s、U=0.140 m/s、U=0.175 m/s时,对润滑油膜压力、膜厚和平均温升的影响如图5所示。
从图5(a)可以看出,回转半径增大,润滑油膜压力显著增大,油膜中心压力变化值大于二次压力峰处压力变化值。从图5(b)可以看出,随回转半径的增大整体膜厚呈现增大的趋势,但最小膜厚变化不明显,且与中心膜厚的差值逐渐增大。从图5(c)可以看出,回转半径对平均温升的影响比较明显,回转半径增大,平均温升变化曲线的斜率显著增大,温度峰愈加尖锐。
回转半径对润滑油膜的影响主要集中在油膜中心位置。卷吸速度与载荷随回转半径的增大同步增大,使得油膜压力增大,接触区内热积聚能力增强,平均温升显著上升。二次压力峰、最小膜厚减速向出口区移动。

图5 回转半径对联轴器润滑特性的影响Fig 5 Effect of the gyration radius on lubrication characteristics of coupling (a) comparison of pressure; (b) comparison of film thickness;(c) comparison of average temperature
2.2 润滑脂特性对联轴器润滑特性的影响
温度变化会对润滑脂的流变特性产生影响,进而影响配合表面的润滑特性。下面主要讨论热弹流脂润滑中,润滑脂特性参数对润滑油膜和平均温升的影响。
2.2.1 润滑脂初始黏度对联轴器润滑特性的影响
根据所设定参数,其他条件不变,卷吸速度U=0.1 m/s,载荷w=9 kN/m,润滑脂初始黏度分别取η0=0.1 Pa·s、η0=0.2 Pa·s及η0=0.3 Pa·s时,对润滑油膜压力、膜厚和平均温升的影响如图6所示。
从图6(a)可以看出,润滑脂初始黏度对润滑油膜压力分布的影响主要反映在二次压力峰处,该处压力随初始黏度的增大显著增加且愈发尖锐,逐渐超过中心压力值。从图6(b)可以看出,初始黏度增大,膜厚呈现均匀增大的趋势,且中心膜厚的变化要大于最小膜厚处,二者膜厚差值逐渐增大。从图6(c)可以看出,黏度增大,平均温升变化曲线的斜率显著增大,中心温度与温度峰差值增大。
润滑脂初始黏度对润滑油膜压力与平均温升的影响主要集中在峰值区域,对膜厚的影响主要集中在油膜中心位置。最小膜厚、二次压力峰和温度峰加速向入口区移动,Hertz接触区变窄,温度峰出现在二次压力峰位置附近。

图6 初始黏度对联轴器润滑特性的影响Fig 6 Effect of the viscosity on lubrication characteristics of coupling (a) comparison of pressure; (b) comparison of film thickness;(c) comparison of average temperature
2.2.2 润滑脂流变指数对联轴器润滑特性的影响
根据所设定参数,其他条件不变,卷吸速度U=0.1 m/s,载荷w=9 kN/m,润滑脂流变指数分别取n=0.75、n=0.85及n=0.95时,对润滑油膜压力、膜厚和平均温升的影响如图7所示。
从图7(a)可以看出,流变指数对润滑油膜压力分布的影响与黏度类似,也体现在二次压力峰处,该处压力随流变指数的增大显著增加且愈发明显尖锐,逐渐超过中心压力值,中心压力变化不明显。从图7(b)可以看出,流变指数增大膜厚随之增大,且增长速率越来越大,油膜中心膜厚与最小膜厚差值逐渐增大。从图7(c)可以看出,流变指数增大,平均温升变化曲线的斜率显著减小,曲线愈平缓,二次温度峰逐渐消失。
润滑脂流变指数增大对润滑特性的影响呈现加速变化趋势。流变指数增大,二次压力峰、最小膜厚向入口区移动,Hertz接触区变窄。二次温度峰出现在二次压力峰位置附近。

图7 流变指数对联轴器润滑特性的影响Fig 7 Effect of the rheological index on lubrication characteristics of coupling (a) comparison of pressure; (b) comparison of film thickness;(c) comparison of average temperature
3 结论
(1)研究联轴器几何参数对其润滑特性的影响,结果表明,输入轴与输出轴轴线夹角、输入轴回转半径减小时,两者二次压力峰、平均温升都大幅下降,但前者膜厚大幅下降,后者膜厚略微下降;增大圆柱滚子半径时,二次压力峰、温升降低,膜厚增大。因此,根据实际工况选择较小回转半径,适当减小轴线夹角,增大圆柱滚子半径有利于改善联轴器润滑特性。
(2)研究润滑脂特性参数对联轴器润滑特性的影响,结果表明,减小润滑脂初始黏度,二次压力峰、膜厚、平均温升大幅降低;增大润滑脂流变指数,二次压力峰、膜厚大幅增大,平均温升大幅降低。因此,根据实际工况适当减小润滑脂初始黏度、增大流变指数有利于改善联轴器润滑特性。

