煤气管道剩余强度评价模型特性对比分析*

王战辉，张智芳，陈锦中，闫君芝，武卫军

(1.榆林学院 化学与化工学院，陕西 榆林 719000；2．陕西省低变质煤洁净利用重点实验室，陕西 榆林 719000；3．陕西有色天宏瑞科硅材料有限责任公司，陕西 榆林 719000)

中国在世界上是最早使用管道运输的国家，原本利用公路、水路、铁路及航空为主要运输工具，如今管道作为第五大运输模式出现在人们的眼前，承担起越来越重的责任，具有愈加保险、环保、节能和无污染等优良特点，越来越受到世界各国的青睐[1]。煤气管道运输是石油化工行业中十分重要的一部分，随着中国综合国力不断进步，已经逐步成为世界第二大经济体以及世界第二大能源消耗国，因此开始大力进行管道建设，全面加快中国能源战略通道和骨干管网的铺设[2]。由于运输管道的工作环境是在土壤中或是直接暴露在大气中，土壤及大气中含有大量的水分，当这些水分浸入管道时，因水分中含有电子，水中的电子会造成管道中的电子发生转移，进而使管道的金属元素发生氧化还原反应，且土壤中的酸碱度不同，土壤中的氧化菌类与还原菌类在不同的酸碱度中与管道发生氧化还原反应，这些因素都会引起管道的腐蚀，因此，腐蚀被认为是管道失效的主要原因。正是由于腐蚀的存在，随着管道使用年份的增加，其力学性能尤其是承压性能会逐年下降。当管道发生腐蚀时，其焊缝本身存在的裂纹以及由于腐蚀而产生的裂纹就会扩大从而引起管道的泄漏，如果不能及时发现并修补这些裂纹，就会引起严重的事故，对国家财产以及人民生命安全造成重大损失[3]。因此，对煤气管道腐蚀现象的研究具有很高的经济效益和社会效益。

腐蚀对煤气管道的正常运行造成了极大的安全隐患，如果能在管道失效前通过计算提前预知管道的剩余强度，那么就可以有效避免一些因管道腐蚀而发生的安全事故，国内外学者对于如何评价腐蚀管道的剩余强度做了大量的研究[4-6]。但是主要应用于油气管道，而对煤气管道研究的很少，而且，常用的剩余强度评价模型的适用性、准确性、保守性均不相同，因此对不同的煤气管道剩余强度评价模型特性进行对比分析是十分必要的[7]。作者首先对常用的剩余强度评价模型如ASME B31G(1984)、ASME B31G(1991)、DNV-RP-F101、PCORRC、BS7910、API 579-1、SHELL92、LPC-1进行了简单的介绍，其次，将以上8种剩余强度评价模型应用于不同的低、中、高钢级管道，通过引入压力比和误差分析不同评价模型的保守性和准确性，从而选择出相应的最佳评价模型。所得结论对于煤气管道的正常运行具有一定的指导意义。

1 不同腐蚀管道剩余强度评价模型介绍

1.1 ASME B31G评价模型

ASME B31G评估模型一般用于评价管材等级较低、服役年限长的管道，属于半经验公式，偏保守，其剩余强度计算公式如下。

ASME B31G(1984)：

式中：L为腐蚀缺陷轴向长度，mm；R为管道外径，mm；c为管道壁厚，mm；F为管道剩余强度，MPa；σs为材料屈服强度，MPa；h为腐蚀缺陷深度，mm；M为膨胀系数。

ASME B31G(1991)：

式中：σf为流变应力，MPa。

1.2 DNV-RP-F101评价模型

DNV-RP-F101评价模型由英国燃气公司(BG)和挪威船级社(DNV)于1999年合作开发，其计算公式如下。

式中：Q为长度校正系数；σf是材料的流变应力，其值取材料的屈服强度,MPa。

1.3 PCORRC评价模型

PCORRC评价模型由美国Battle实验室开发完成，主要用于含腐蚀缺陷中高强度等级管道由于塑形失稳导致失效的评估，PCORRC评价模型剩余强度计算公式如下。

式中：σf取材料的屈服强度，MPa；Rt为内外径的平均值。

1.4 BS7910评价模型

BS7910模型由英国标准委员会于1999年发布，并在计算公式中采用抗拉强度代替流变应力。其计算公式如下。

1.5 API 579-1评价模型

在API 579-1 评价模型中没有使用流变应力，而是使用了材料本身的屈服强度。API 579-1的剩余强度计算公式如下。

Mt=1.001-0.014 195λ+0.290 90λ2-0.096 420λ3+0.020 89λ4-0.003 054λ5+2.957×10-4λ6-1.846 2×10-5λ7+7.155 3×10-7λ8-1.563 1×10-8λ9+1.465 6×10-10λ10

其中当β的计算值大于20时，取20。

1.6 SHELL 92及LPC-1评价模型

SHELL92评价模型是由 RITCHIE D和LAST S在1995年第10届干线管道研究联合技术会议上提出。LPC-1评价模型与SHELL92类似，都是在ASME B31G方法上改进而来的，SHELL92评价模型流变应力选用材料最小拉伸强度的0.9倍，LPC-1评价模型则直接选用材料最小拉伸强度。剩余强度计算公式如下。

SHELL92：

式中：δb为材料拉伸强度，MPa。

LPC-1：

2 8种评价方法的计算结果及适用性分析

将以上8种剩余强度评价模型应用于不同的低、中、高钢级管道，通过引入压力比和误差分析不同评价模型的保守性和准确性，从而选择出相应的最佳评价模型。

2.1 8种评价方法的计算结果

收集整理了X42、X46、X52、X56、X60、X65、X70、X80、X100等囊括低、中、高钢级管道的27组含腐蚀缺陷的实验数据[8-10]。用序号1～27表示。不同钢级含腐蚀缺陷管道的实验数据见表1。

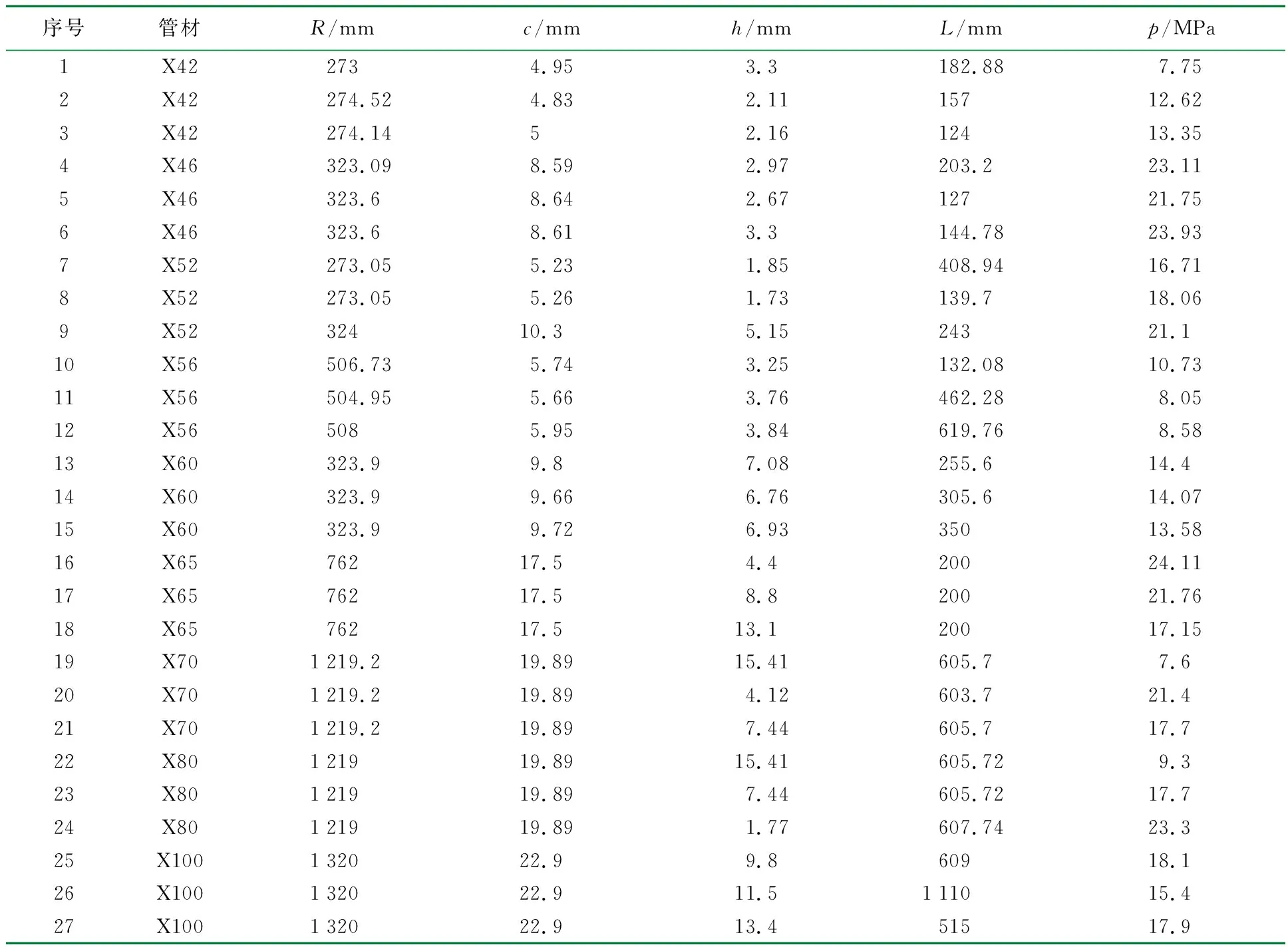
表1 不同钢级含腐蚀缺陷管道的实验数据

将以上27组数据代入ASME B31G(1984)、ASME B31G(1991)、DNV-RP-F101、PCORRC、BS7910、API 579-1、SHELL92、LPC-1 8种剩余强度评价模型进行计算，计算结果见表2。

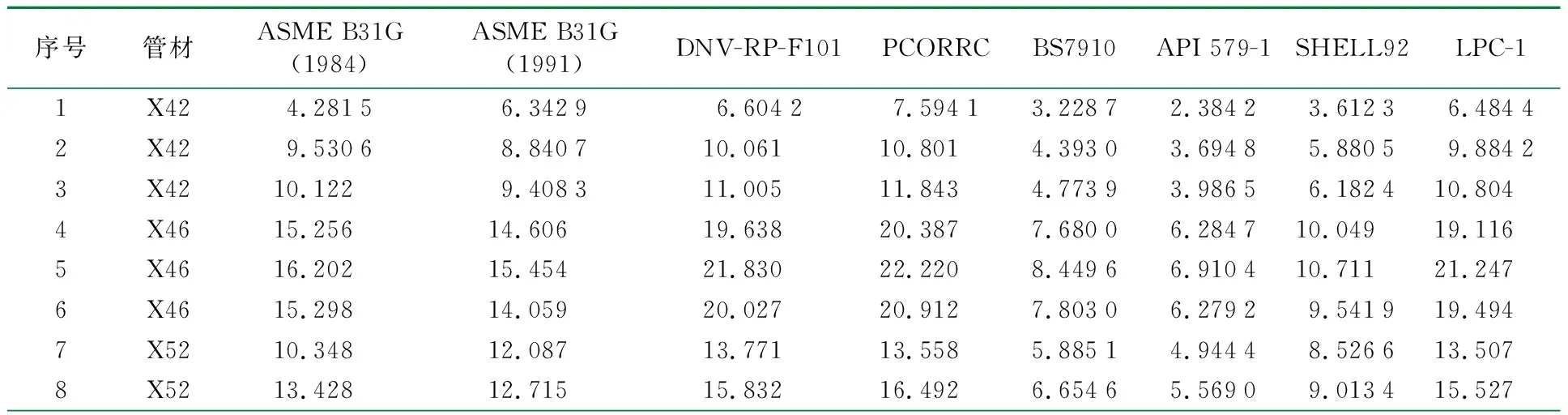
表2 8种评价模型剩余强度计算结果

续表

2.2 8种评价模型的保守性分析

引入参数压力比A，其中，A=爆破压力/计算剩余强度。A<1，表明评价结果呈现激进性，即计算剩余强度大于爆破压力；A=1，表明评价结果与实验爆破压力一致，最为理想；A>1，表明评价结果保守，即计算剩余强度小于爆破压力。

低钢级管道压力比见图1。

图1 低钢级管道压力比图

由图1可知，对于X42、X46、X52 3种低钢级管道而言，保守性最理想的是DNV-RP-F101评价模型，其压力比主要分布在1.0～1.3；保守性最差的是API 579-1评价模型，其压力比主要分布在3.1～3.7。因此DNV-RP-F101评价模型最适用于低钢级管道。

中钢级管道压力比见图2。

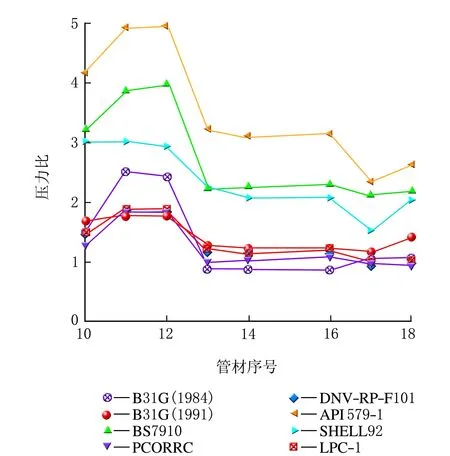
图2 中钢级管道压力比图

由图2可知，对于X56、X60、X65 3种中钢级管道而言，保守性最理想的是DNV-RP-F101评价模型，其压力比主要分布在1.0～1.8；保守性最差的是API 579-1评价模型，其压力比主要分布在2.5～5.0。因此DNV-RP-F101评价模型最适用于中钢级管道。

高钢级管道压力比见图3。

图3 高钢级管道压力比图

由图3可知，对于X70、X80、X100 3种高钢级管道而言，保守性最理想的是PCORRC评价模型，其压力比主要分布在0.8～1.2；保守性最差的是API 579-1评价模型，其压力比主要分布在2.0～3.3。因此PCORRC评价模型最适用于高钢级管道。

2.3 8种评价模型的误差分析

引入参数计算误差，其中，计算误差=(爆破压力-计算剩余强度)/爆破压力

计算误差为正，说明爆破压力大于计算剩余强度；计算误差为负，说明计算剩余强度大于爆破压力。

低钢级管道误差分析见图4。

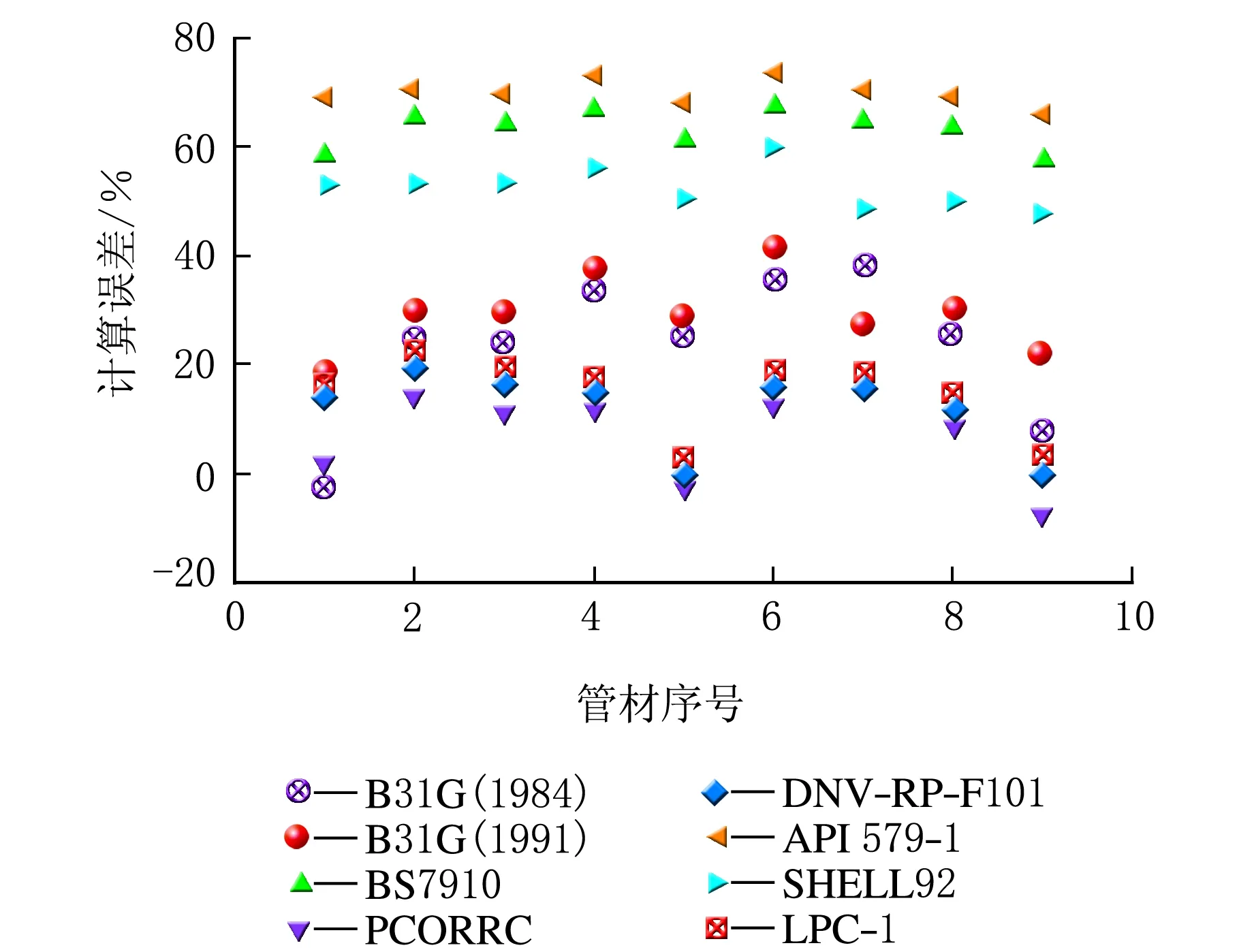
图4 低钢级管道的误差分析图

由图4可知，对于X42、X46、X52 3种低钢级管道而言，误差最大的是API 579-1评价模型，主要分布在65%～75%；误差最小的是PCORRC评价模型，主要分布在-8%～13%。因此，在低钢级管道的剩余强度评价的误差分析中，表现最好的是PCORRC评价模型。

中钢级管道误差分析见图5。

图5 中钢级管道的误差分析图

由图5可知，对于X56、X60、X65 3种中钢级管道而言，误差最大的是API 579-1评价模型，主要分布在58%～80%；误差最小的是PCORRC评价模型，主要分布在-5%～20%。因此，在中钢级管道剩余强度评价的误差分析中，表现最好的是PCORRC评价模型。

高钢级管道误差分析见图6。

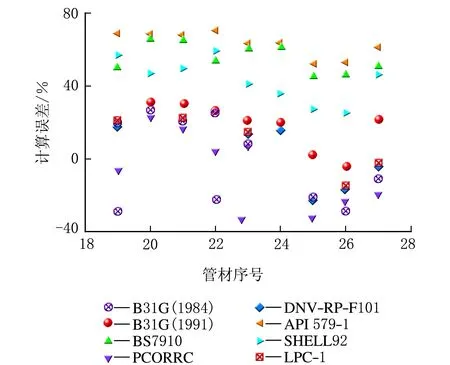
图6 高钢级管道的误差分析图

由图6可知，对于X70、X80、X100 3种高钢级管道而言，误差最大的是API 579-1评价模型，主要分布在50%～70%；误差最小的是DNV-RP-F101评价模型，主要分布在-15%～0%。因此，在高钢级管道剩余强度评价的误差分析中，表现最好的是DNV-RP-F101评价模型。

3 结 论

(1)从压力比出发，对于低中钢级管道，DNV-RP-F101评价模型保守性最理想，对于高钢级管道，PCORRC评价模型保守性最理想，经济性能优良；对于所有钢级管道，API 579-1评价模型最为保守，经济性能差，不适合进行剩余强度评价；

(2)从误差分析出发，对于低中钢级管道，PCORRC评价模型误差最小，对于高钢级管道，DNV-RP-F101评价模型误差最小，最准确，稳定性好；对于所有钢级管道，API 579-1评价模型误差最大，不适合进行剩余强度评价。