基于随机生产模拟的发电系统储能容量优化配置

罗 定

(中国能源建设集团湖南省电力设计院有限公司，湖南省 长沙市 410011)

0 引言

储能是支撑新一代电力系统和能源互联网发展的关键技术，对我国能源转型与电网高质量发展具有重要意义[1]。蓄电池储能系统(battery energy storage system，BESS)具有良好的响应特性及能量容量，且不受地理位置、气象条件等因素的影响，是一项良好的调峰手段[2-3]。目前，储能建设成本通常高于常规机组，发电系统中储能容量配置过大将会使发电成本大大提高，而过小则其参与调峰带来的经济效益又不明显。因此，在发电系统扩展规划问题中进行储能容量配置的事前分析至关重要。

有关储能容量优化配置的研究中，常用系统综合成本最小作为目标[4]，而随机生产模拟正是可在在考虑机组随机故障及负荷随机性的情况下，通过模拟发电机组的生产情况计算出最优运行方式下电力系统的可靠性指标、发电量以及生产成本的算法[5-6]。储能参与系统调峰，将影响系统的运行方式，进而表现在系统可靠性与各类成本的改变，而这些因素均可用随机生产模拟进行度量[7-8]。目前，随机生产模拟已广泛应用于发电系统的灵活性改造、生产计划制定以及新能源消纳评估等研究领域中。文献[9]基于随机生产模拟方法在中长期时间尺度下给出了机组年度发电量和广义成本计算方法，以火电机组灵活性改造广义成本最低为目标，建立了火电机组灵活性改造容量规划模型。文献[10]运用随机生产模拟建立了反映发电侧调节能力的运行备用容量与可靠性之间的联系，通过日前发电-备用双层模型进行系统发电计划的优化。文献[11-12]使用服从一定分布的离散型随机变量描述新能源出力和消纳空间的随机性，通过概率分布间的运算，使用含新能源电力系统的随机生产模拟，快速求解风、光消纳空间与弃风、弃光概率。以上研究成果中，随机生产模拟发挥了其原理简单，计算求解简便的优势。本文将随机生产模拟应用于发电系统储能容量优化配置中，能够简洁有效地解决发电系统储能容量长期规划问题。

本文首先在现有随机生产模拟算法的基础上，将储能的充放电分别等效为负荷和发电机组，给出了含储能的发电系统随机生产模拟算法；然后以储能参与调峰后发电系统的综合成本最小为目标，计及系统、电源以及储能的运行约束，建立了发电系统储能容量优化配置模型；再通过随机生产模拟求解储能充放电调度策略和最优容量；最后对修改的IEEE-RTS 79算例进行仿真模拟，结果表明所提方法可得到经济的储能容量配置方案。

1 含储能的发电系统随机生产模拟算法

电池储能系统充放电数学模型如下所示：

(1)

随机生产模拟能够计算出发电系统的各项可靠性与经济性指标。基于展开型表述的随机生产模拟方法利用时序负荷曲线，在满足上述模型约束下，根据经济性安排各机组加载运行形成展开型结构，保留了电源与负荷的时序性[5]。该方法同样能保留储能电池电荷状态(state of charge，SOC)的时序性，处理BESS非常方便。

对含BESS的发电系统进行随机生产模拟时，根据系统运行调度策略依次加载机组，若某机组加载后储能满足充电条件进行充电，则将该机组加载次序编号记为kch。储能的充电功率由前kch台加载的机组提供，不会影响该时刻系统电力不足概率、电量不足期望值等系统可靠性指标和后续加载机组发电量。若某台机组加载后储能达到放电条件，则将该机组加载次序编号记为kdis。储能将作为等效放电机组出力，储能等效机组的加载次序为kdis+1。此时储能承担了部分负荷，有助于提高系统该时刻的可靠性，并减少后续加载的高发电成本机组的发电量，但不会影响前序加载机组的发电量。

1.1 储能充电

当前kch台加载机组的出力之和大于负荷Lt时，系统对储能充电，即

(2)

运行过程中储能可接收的充电功率受最大容量、当前时刻容量状态、最大充电功率等自身参数的限制：

(3)

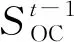
储能充电之后需更新SOC：

(4)

若系统对储能充电，充电功率将由前kch台机组提供。此时前kch台机组承担的负荷需要进行修正：

(5)

(6)

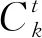
1.2 储能放电

当前kdis台机组出力之和小于负荷Lt时，储能放电，即

(7)

运行过程中储能可提供的放电功率受最小容量、当前时刻容量状态、最大放电功率等自身参数的限制：

(8)

式中：SOCmin为储能最小SOC；Pdis_max为最大放电功率；ηdis为放电效率。

储能放电之后需更新SOC：

(9)

考虑储能的随机故障，设储能强迫停运率为pb_FOR，将储能放电等效为两状态的常规机组并作为第kdis+1台机组继续加载。

2 发电系统储能容量优化配置模型

由于发电系统全年运行情况不同，储能容量配置时需要考虑全年的各种运行情况。本文以风电为例，考虑风电与负荷季节性的影响，选取春夏秋冬4个季节的典型日风电出力场景和负荷曲线整合1个考察周期，建立基于随机生产模拟的发电系统储能容量配置模型。设置ΔEb为优化系统调峰储能容量的步长，步长越小结果越精确，但执行随机生产模拟算法的次数越多，求解效率越低，可综合计算精度与效率要求设置ΔEb。优化的解为最优储能容量Eb_zy、最优储能充放电调度策略kch_zy与kdis_zy。

2.1 目标函数

含储能的发电系统各类成本主要包括：生产成本、环境成本、可靠性成本和储能成本。储能的调峰效应使负荷曲线平滑，减少了峰谷荷时长，使常规发电机组在更经济的模式下运行，相应的经济效益可以量化为常规机组的生产成本降低。储能的充放电使常规机组的发电量变化，环境成本相应变化；储能作为快速作用的储备资源，可以有效提高电力系统的可靠性，该部分的经济效益可以量化为可靠性成本的降低。另外，储能成本与其额定功率、容量以及利用率都有关。受各种因素的影响，系统的综合成本是变化的，发电系统储能容量优化的目标是使得综合成本最小，即可获得最大的经济效益。以全系统的综合成本最小为目标函数的储能容量优化模型如下：

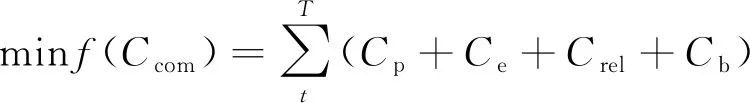
(10)

式中：Ccom为系统的综合成本；Cp为系统的生产成本；Ce为系统的环境成本；Crel为系统的可靠性成本；Cb为系统的储能成本。

1) 生产成本。

由于随机生产模拟可以计算出考察时间内各机组的发电量ek，各常规机组启停次数ng；已知各常规机组单位发电量的燃料成本cf.g,、启停成本cn.g，各机组单位发电量的运行维护成本co&m.k，可知全系统的生产成本为

(11)

2) 环境成本。

已知各常规机组单位发电量应承担的环境成本为ce.g，可知考察时段内，系统的环境成本为

(12)

3) 可靠性成本。

随机生产模拟可计算出系统的电量不足期望值EENS，通过增加调峰备用，EENS会越小；但调峰备用容量越大，产生的备用成本越高。系统可靠性成本Crel定义为综合考虑调峰备用成本及系统可靠性提高效益的成本：

Crel=αRcbp+(1-α)cvEENS.R

(13)

式中：cbp为系统单位备用容量成本；EENS.R为备用为R时系统EENS值；cv为单位电量的缺电成本；α为系数。

4) 储能成本。

电池储能电站的成本包括初始投资成本和运行维护成本。假设储能系统在使用周期内正常运行，即不考虑其设备更换。本文考虑储能的使用寿命和投资收益率先将储能的一次性投资成本等值为年投资成本，再计及年运行维护成本，最后将储能的年总成本在考察时间内进行分摊。具体公式如下：

式中：λE和λP分别为储能的容量成本和功率成本；Eb.m和Pb.m分别为储能的额定容量与额定充放电功率；fcr为资本回收系数；λo&m为储能系统单位容量年运行维护费用；nb为储能装置的寿命；r为折旧率；T为考察时间。

2.2 约束条件

基于随机生产模拟的发电系统电池储能容量优化配置模型的约束条件包括系统运行约束、电源运行约束和储能运行约束。

1) 系统运行约束：

(16)

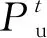
2) 电源运行约束：

(17)

式中：Pu.min机组u的最小技术出力限制；Pw.total为风电场总的装机容量。

3) 储能运行约束：

(18)

3 储能容量优化整体流程

基于随机生产模拟的发电系统电池储能容量优化配置流程如图1所示。主要步骤如下文所述。

1) 输入原始系统源、荷的各类时序数据，对风、荷进行典型场景聚类整合处理。

2) 对原始系统进行随机生产模拟，确定储能充放电位置的大致范围。

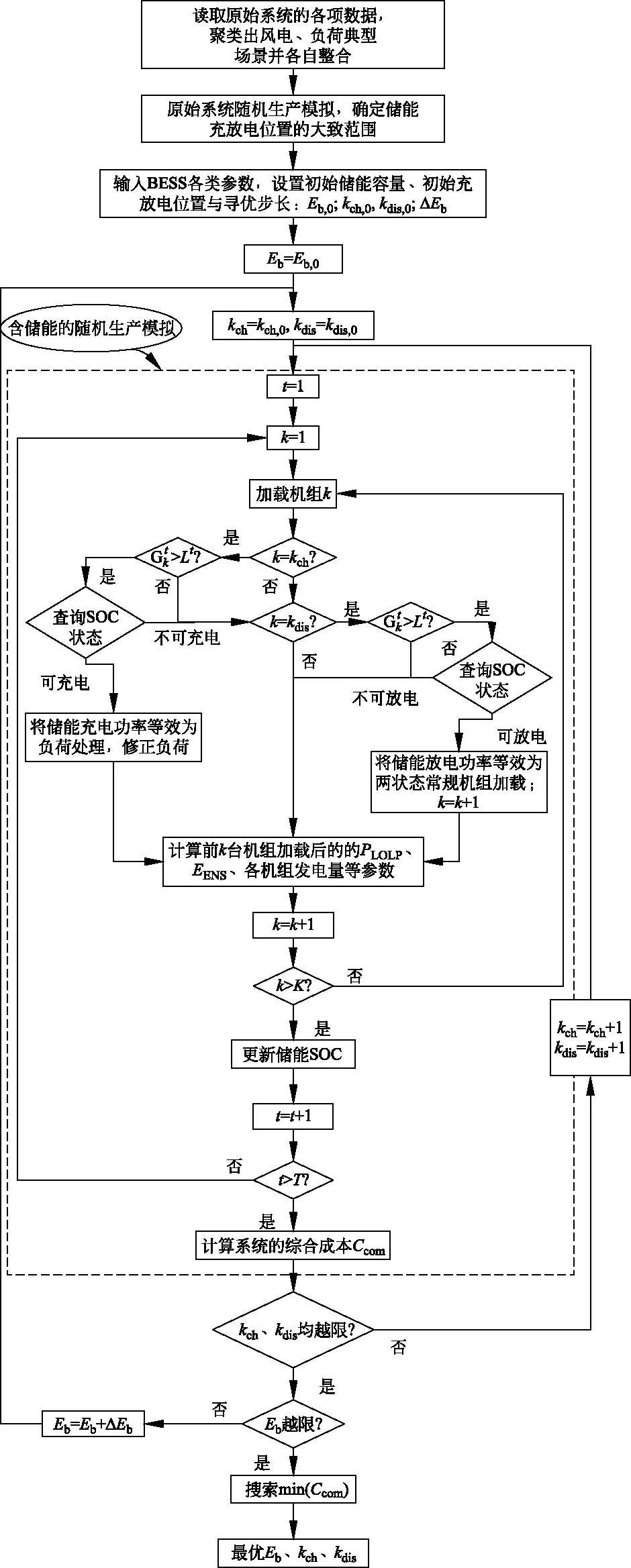
图1 基于随机生产模拟的发电系统电池储能容量优化配置流程

3) 输入BESS各类参数，设置初始储能容量、初始储能充放电位置以及寻优步长。

4) 利用公式(10)—(18)建立储能容量优化模型。

5) 利用公式(1)—(9)含储能的随机生产模拟算法求解新系统的综合成本Ccom。

6) 判断kch与kdis是否均越限：是则转步骤7)；否则更新两者后转步骤5)。

7) 判断Eb是否越限：是则转步骤8)；否则更新Eb后转步骤5)。

8) 搜索最小综合成本min(Ccom)下的储能容量Eb_zy、储能充放电调度策略kch_zy与kdis_zy。

4 算例分析

4.1 算例说明

本文算例基于IEEE-RTS 79测试系统，32台发电机，总装机容量为3 405 MW，年最大峰荷为2 850 MW。发电机组的各类参数来自文献[13-16]，详见附录A表A1。其中，3号水电机组用1个300 MW的风电场代替，系统的装机容量不变。风电场包含了60台额定功率为5 MW的风力发电机；假设风机间相互距离较远，忽略其相关性。将IEEE-RTS 79测试系统中春夏秋冬4个季节的日负荷数据分别取平均值形成4个季节的典型日负荷，然后组合成一条时序负荷曲线作为储能容量优化配置的考察时间，共96 h，如附录A图A1。风电出力的数据取自比利时电力运营商Elia[17]公开的2017年风电运行数据，采用K-means聚类分析[18]得到春夏秋冬4个季节的典型日的小时数据，并整合成96h风电出力曲线，见附录A图A2。

设置以下2个场景。

场景1：上述原始系统。

场景2：含BESS的待优化系统。在场景1系统中加入额定充放电功率为20 MW的锂电池电站；储能容量暂定为80 MW·h。电站的SOC控制在0.1～0.9，初始SOC设为0.1。锂电池电站的具体参数[19]见表1。

4.2 BESS调峰范围的确定

首先对场景1进行随机生产模拟，得到系统电力不足概率、电量不足期望值、各机组的期望发电量与期望启停次数以及各类经济性指标，见表2—3中场景1部分。表3中，从上至下的顺序为生产模拟中机组的加载顺序。

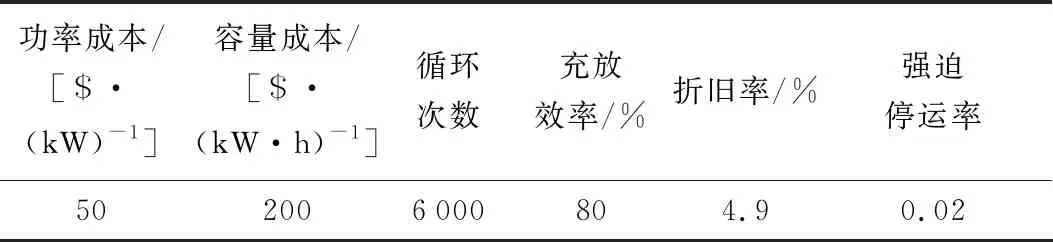
表1 锂电池电站参数

通过观察各机组的期望发电量与启停次数可知：9、8号机组为常开的基荷机组；6、4和7号机组为日常调峰机组；5、1和2号机组较少参与发电，为用于故障与检修的备用机组。在该系统中，模拟BESS电站参与调峰的充放电加载位置应位于6、4和7号机组所在加载位置附近，即图2绿色阴影的范围中。

4.3 BESS参与调峰的经济性分析

在场景2中，将BESS参与调峰的充电位置设在6号机组之后，如图2红色圆点位置，即6号机组加载完毕后BESS若满足充电条件将进行充电；将BESS参与调峰的放电位置设在4号机组之后，如图2黄色圆点，即4号机组加载完毕后BESS若满足放电条件将进行放电。

经过随机生产模拟得到场景2系统在上述BESS充放电调度方案下的可靠性指标、各机组的期望发电量与期望启停次数以及各类经济性指标，见表2—3中场景2部分。较于场景1，场景2中的电力不足概率与电量不足期望值均减少，可见BESS参与调峰提高了系统的可靠性，降低了可靠性成本。场景2中发电成本较低的8、6号机组的发电量增加，发电成本较高的7、5、1和2号机组的发电量减少，说明BESS的调峰作用可使高生产成本机组承担的负荷转移到低生产成本机组，从而降低系统的生产成本。

图3为场景2的储能SOC时序变化图。

表2 随机生产模拟结果

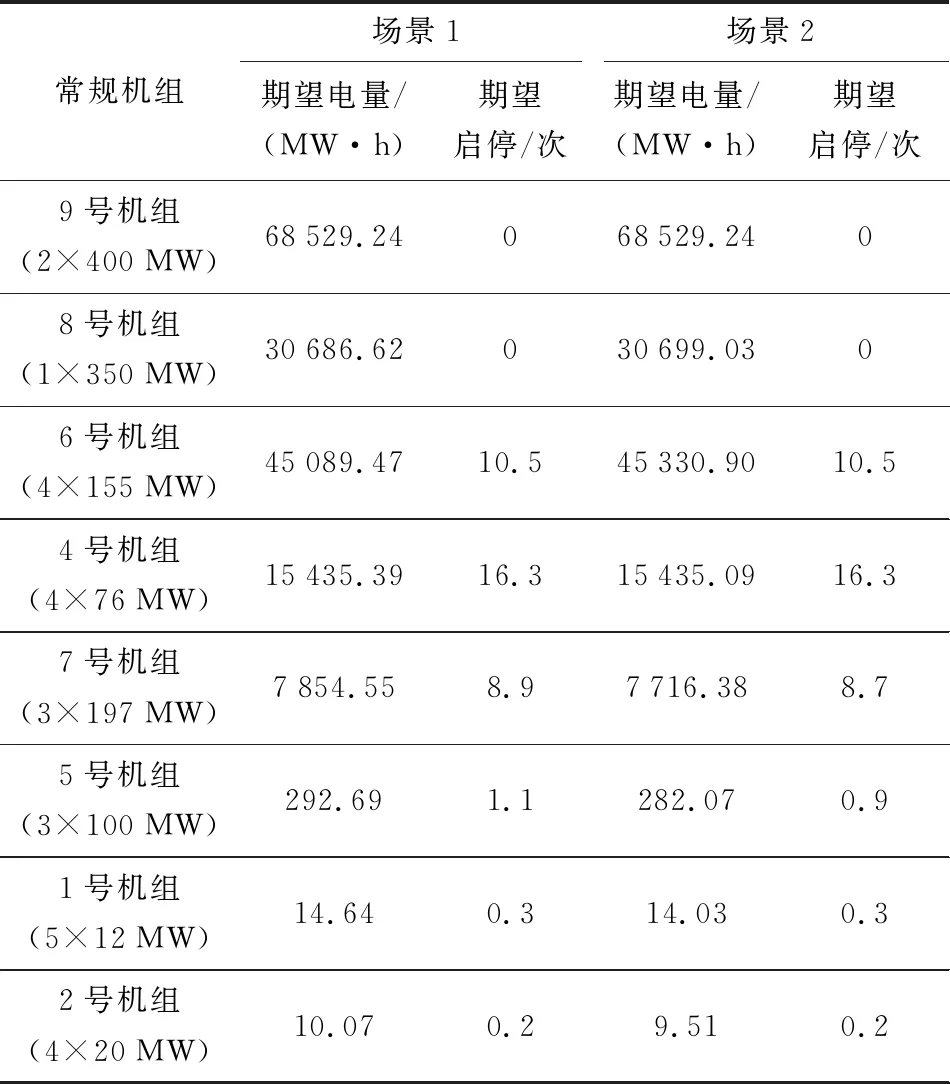
表3 各机组的期望发电量与期望启停次数

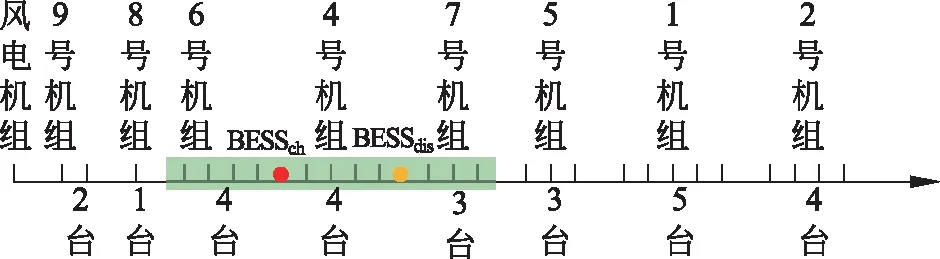
图2 机组加载顺序与储能充放电加载范围

图3 储能SOC时序模拟曲线

4.4 BESS参与调峰的最优容量配置

由4.2节得知，BESS参与调峰的充放电可设置在6、4和7号机组附近的12个位置，如图4所示。

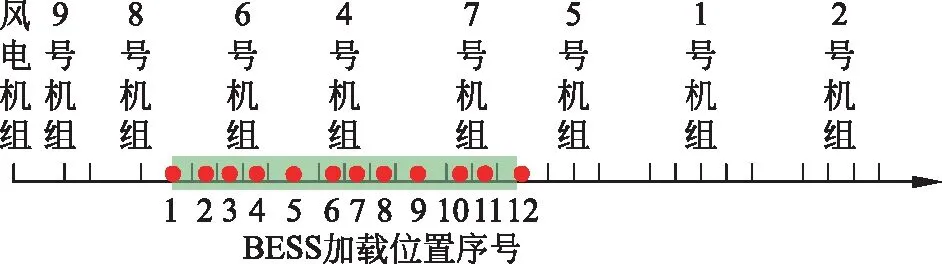
图4 BESS所有加载位置

用C#编程对场景2系统进行储能容量优化配置。其中，风电出力优先消纳，其加载次序为1；储能充放电的加载位置kch和kdis的初始值分别设为4、4；储能容量的初始值设置为Eb,0=0 MW·h；变化步长为ΔEb=5 MW·h。

最终优化的结果为：kch_zy=13，kdis_zy=13；Eb_zy=120 MW·h。此时的系统综合成本为4.155 8×106$；综合成本随储能容量变化如图5所示。即本系统中：在储能电站的额定充放电功率为20 MW的情况下，该发电系统的储能容量为120 MW·h且在7号机组的第1台发电机投运完毕后储能进行充放电时最为经济。相对于含储能但未优化的场景2，优化后综合发电成本降低3.5×104$；相对于不含储能的场景1，综合发电成本降低6×104$。

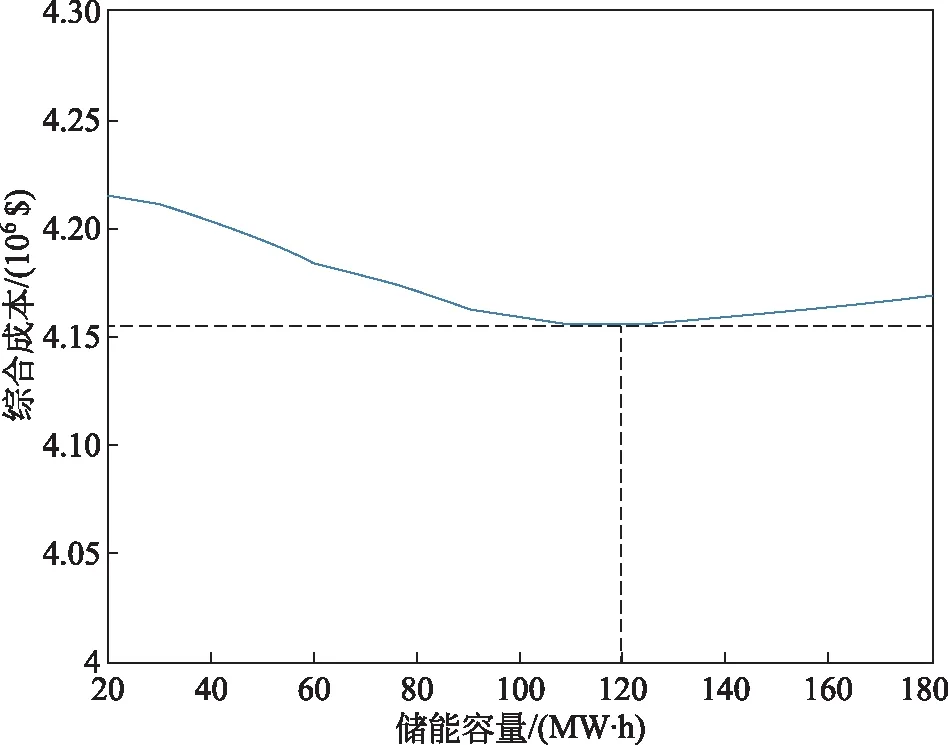
图5 系统综合成本变化曲线

图6为场景2经优化储能充放电策略及容量后的储能SOC时序变化图。对比图3可见，储能的利用率得到了显著提高。

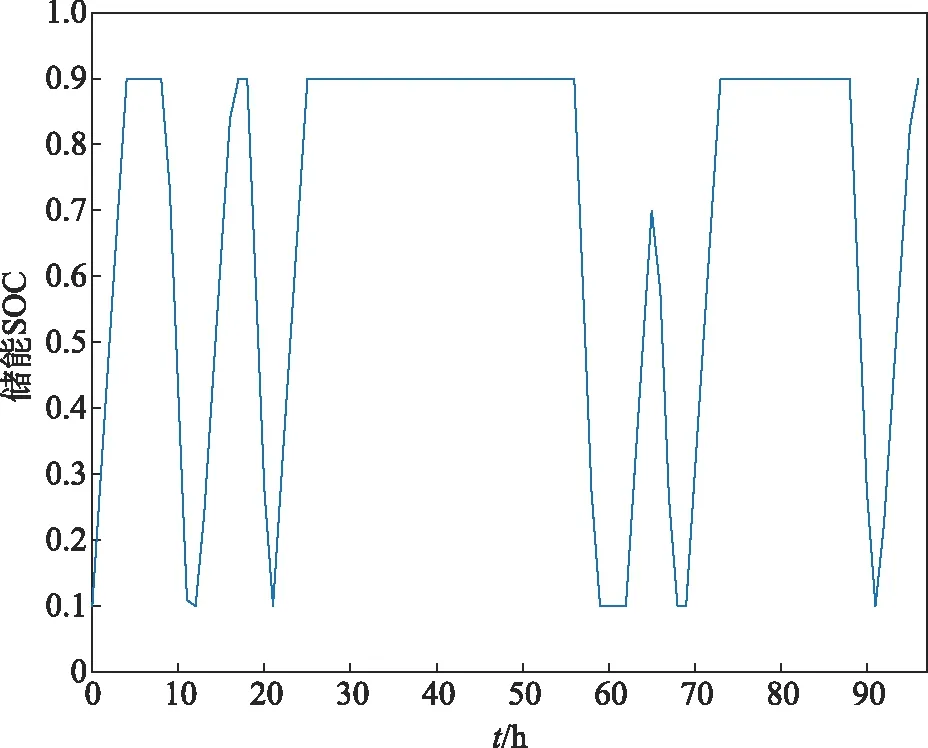
图6 优化后的储能SOC时序曲线

5 结论

1) 本文基于随机生产模拟的发电系统储能优化模型计及了源、荷、储的时序性，能同时对储能容量及充放电策略进行优化，并具有原理简单、求解简便的优势。在发电系统规划时，能有效地为电池储能电站的容量配置提供理论指导。

2) 本文算例模拟系统生产时长为96 h，若换算成一年，则优化储能容量及充放电策略后每年可为该发电系统节省成本约3.20×106$。从系统综合成本效益的角度来看，储能的配置容量并不是规模越大越好，合理规划储能容量可产生良好的经济效益。