连续曲线梁桥在汽车荷载作用下的动力响应分析

任剑莹， 李晓东, 霍 静

(1.石家庄铁道大学 省部共建交通结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；2.石家庄铁道大学 工程力学系，河北 石家庄 050043；3.中交铁道设计研究总院有限公司 桥隧处，北京 100089；4.中国铁路兰州局集团有限公司 银川工务段银川桥隧车间，宁夏 银川 750000)

0 引言

由于曲线梁桥能较好地适应地形和路线限制的需要，且线形平顺流畅、明快，因此在立交工程和高架桥中得到了广泛应用[1]。国内外学者对车-桥耦合系统动力学分析的研究多集中在直线桥上[2-7]，而对于公路曲线桥涉及较少[8]。由于汽车荷载的复杂性和不确定性以及曲线桥的“弯-扭耦合”现象，使得公路曲线桥的研究相当棘手。国内外学者对其进行研究分析，多通过现场试验、解析计算、数值模拟等方法获得曲线桥的各种动力响应及动力放大系数，并取得了许多有益的结果[9-19]。通常认为桥梁结构的静动力分析无须考虑材料非线性，但是随着高墩大跨桥梁结构的不断涌现，在桥梁结构承载力分析、稳定分析中均已考虑材料非线性的影响[20-25]，而在车-桥相互作用系统动力分析中还鲜有涉及。

因此，本文基于某座四跨连续曲线箱梁桥的现场动力实验，采用通用非线性有限元分析软件ABAQUS计算公路曲线桥在车辆荷载作用下的动力响应，并与实验数据进行对比，验证模型的正确性，在此基础上进一步研究偏载、车速、载重以及材料非线性等因素对该公路曲线桥动力响应的影响，可为后续研究桥面沥青铺装层的动力响应及破坏机理、大跨曲线桥的动力响应、损伤识别、健康监测等提供重要的参考。

1 曲线桥有限元模型

1.1 工程简介

图1为江西某单箱双室钢筋混凝土曲线桥的桥型布置图。该桥纵向坡度为7%，跨径为15 m+15 m+15 m+17 m。平均曲线半径为50 m。该曲线桥为重载卡车运输用桥，采用抗扭支座，中间墩为固定支座。该桥在1#、2#和3#墩帽梁中间部位设置了防止梁体横向大偏移的限位槽，有限元模型中在此处约束梁体径向平移和竖向位移。称此约束为“中间支座”。

图1 曲线桥桥型布置图

图2 曲线箱梁横截面示意图(单位：cm)

图2为该曲线桥横截面示意图。该箱梁顶板宽度为12 m，平均厚度0.28 m；底板宽度8 m，厚度0.25 m；腹板厚度沿曲梁长度有所变化，这里取厚度平均值0.65 m；翼缘板悬臂长2 m。顶板之上铺设有厚度为0.1 m的沥青路面。

1.2 建立有限元模型

采用大型通用有限元分析软件ABAQUS建立曲线桥梁体模型。单元类型采用C3D8R减缩积分单元，该单元类型计算用时少，位移结果较精确，对于扭曲现象具有很好的适用性。全桥共有59 648个单元和81 469个节点。为了避免出现应力集中，边界约束条件按实际支座的布置情况施加在箱梁底板相应于支座位置处的接触面上。曲线桥模型如图3所示。

实验车辆采用东风重卡，前轮距3.8 m，后轮距1.45 m，总质量31 t。有限元计算模型中将车辆轮胎力简化为6组0.5 m×0.5 m的面力，简化荷载图如图4所示。在ABAQUS/Standard中，采用隐式动力分析，利用Fortran语言编写荷载移动的Dload和Utraction子程序，模拟车辆经过全桥的整个过程，分析全过程中曲线桥的动力响应。

图3 曲线桥有限元模型

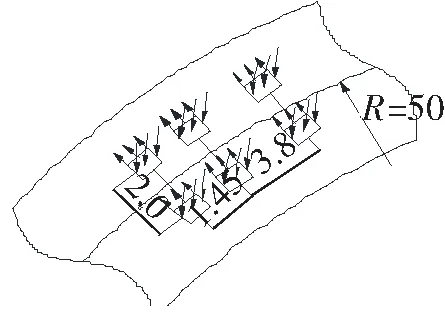
图4 汽车荷载简化示意图(单位：m)

1.3 钢筋混凝土材料本构关系

该钢筋混凝土曲线桥采用的是C50混凝土(密度ρc=2 500 kg/m3)，Vc=500 m3，质量为Mc=1 250 t，共使用钢筋Ms=184.44 t。钢筋质量占全桥质量的比重较大，对桥梁的刚度有较大影响，所以建模时必须考虑钢筋的影响。在此使用等效密度和等效刚度建立有限元模型。

等效密度

(1)

等效弹性模量

(2)

式中,As、Ac分别为横截面钢筋和混凝土的面积；Es为钢筋弹性模量；Ec为混凝土弹性模量。

采用以上材料属性对曲线桥进行建模计算，分析横向位置、车速和载重对曲线桥各动力响应的影响情况。

为了分析材料非线性对该桥动力响应的影响，结合文献[26]和文献[27]拟合出图5中实线所表示的混凝土单轴压缩和单轴拉伸应力-应变曲线，由该曲线可知，应力和应变一开始就是非线性的关系，这增大了使曲线桥进入材料非线性的荷载范围，以便于对比分析材料非线性的影响情况。

图5 拟合非线性本构关系

2 模型验证

该桥现场实验(见图6)采用脉动法进行自振频率测试，并采用应变仪和百分表测得典型截面处的应变分布以及竖向挠度。同时采用前述建立的该桥有限元计算模型，模拟现场实验工况，得到有限元计算结果。表1为该桥竖向一阶和二阶频率的实测值和有限元计算值对比情况。表2为载重汽车分别以5 km/h、10 km/h、15 km/h的速度通过曲线桥时，第三跨跨中挠度的实测值与计算值的对比情况。表3为第三跨跨中截面在偏载工况下(3辆卡车并排紧靠，最外侧卡车轮胎紧贴外侧挡板于第三跨跨中)挠度的实测值与计算值的对比情况。

图6 现场实验

表1 该桥前两阶频率的实测值与计算值对比

表2 不同车速时第三跨跨中截面的挠度实测值与计算值对比

表3 外偏载工况下第三跨跨中底板的挠度实测值与计算值对比

由表1可以看出，有限元计算模型的固有频率与该曲线桥的实测频率很接近，误差最大为3.50%，说明有限元计算模型的刚度和约束条件接近于实际桥梁结构。由表2可知，重载车辆以不同车速通过曲线桥时，挠度误差基本都在6%以下，误差的绝对值只有0.01 mm。由表3可以看出，静载偏载工况下，底板挠度的计算值和实测值误差范围都在11%以内。因此，所建有限元计算模型能够较好地模拟实际桥梁。

3 不同汽车荷载工况对曲线桥动力响应的影响

基于上述验证后的有限元模型，通过改变荷载横向加载位置、荷载通过全桥的时间和荷载大小讨论了车辆行驶位置、车速、车辆载重对曲线桥跨中位移、扭转角和支反力等的影响情况。由于篇幅有限，只列出了各参数对第二跨跨中和2#墩支座处动力响应的影响情况，其他各跨规律相似。

3.1 车辆横向位置的影响

车辆载重为30 t，以15 km/h的速度通过曲线桥，研究车辆分别沿曲线桥内侧(e=+3 m即内偏)、中线(e=0 m即中间)和外侧(e=-3 m即外偏)行驶时(见图7)对第二跨跨中底板中腹板下(B点处)竖向位移、横向位移、截面扭转角(假设向外侧扭转角度为正)和2#墩内侧支座竖向支反力的影响，对比情况如图8所示。

图7 荷载横向加载及底板A点、B点、C点位置示意图

图8 车辆横向位置对曲线桥动力响应的影响

图8可以看出：(1)内偏载引起的跨中截面底板中点的竖向位移最小，中载引起的向下的位移最大，但是外偏载引起的向上的位移最大，说明外偏载对临跨结构的竖向位移影响最大。(2)中载和内偏载引起的B点的横向位移有正有负，外偏载引起的横向位移全部为正值，说明外偏载会使曲线桥梁体有向外侧滑移的趋势。(3)即使车辆沿中线行驶仍然会引起跨中截面向外侧扭转。车辆偏载行驶过程中，引起跨中截面最大扭转角为0.005°，要远大于沿中线行驶时的0.001°，说明由于偏载引起的结构的扭转效应对桥梁的动力响应具有较大的影响，这与文献[15]的结论相一致。另外，外偏载引起的最大截面扭转角0.005°大于内偏载的0.002 5°，说明外偏载对曲线桥跨中截面的扭转影响更大。(4)外偏载工况下，当荷载移动到2#墩位置时引起内侧支座的竖向支反力很小，甚至产生负的支反力。

表4～表6列出了各工况下第二跨跨中箱梁底板不同位置的最大响应值和2#墩各支座的竖向支反力的最大值。

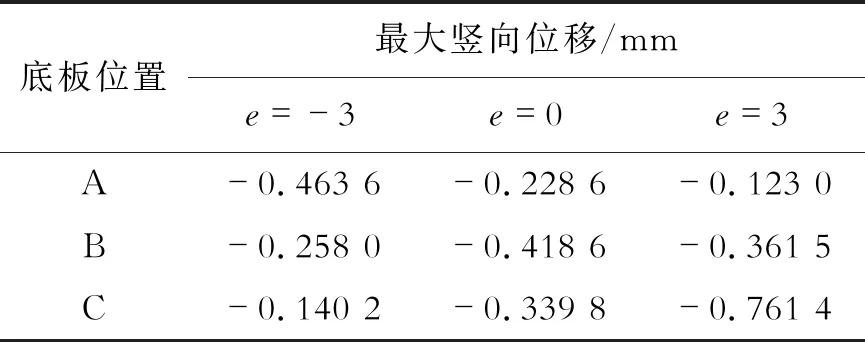
表4 偏载对不同位置处竖向位移最大值的影响

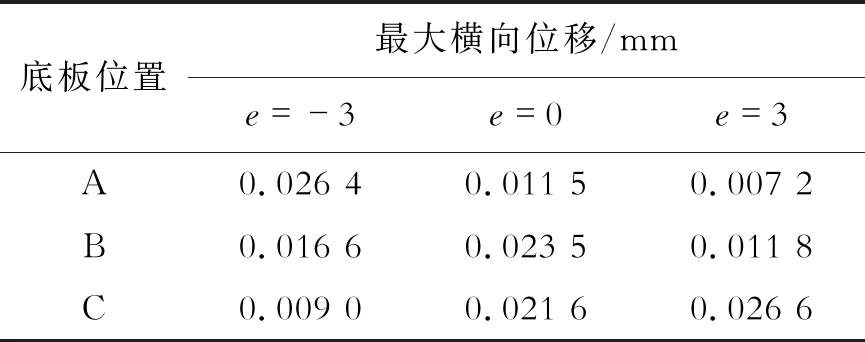
表5 偏载对不同位置处横向位移最大值的影响

由表4～表6可以看出：(1)内偏载时，A点各动力响应最大；中载时，B点各动力响应最大；外偏载时，C点各动力响应最大。(2)无论竖向位移、横向位移还是竖向支反力最大的响应值均出现在外偏载工况下，说明车辆沿外侧行驶时将引起桥梁更大的动力响应，是车辆行驶的最不利工况。

3.2 车速的影响

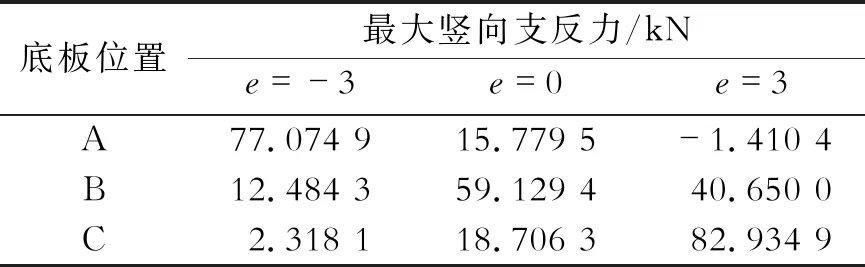
表6 偏载对竖向支反力最大值的影响

桥梁离心力是一种伴随着车辆在弯道行驶时所产生的惯性力，其以水平力的形式作用于桥梁结构，是弯桥横向受力与抗扭设计计算所考虑的主要因素[28]。《公路桥涵设计通用规范》(JTG D60—2015)中明确规定：曲线桥应计算汽车荷载引起的离心力。从离心力的计算公式Fc=mv2/r可以看出速度是影响离心力大小的控制因素。图9为汽车荷载为30 t时，移动速度对曲线桥第二跨跨中B点处竖向位移、横向位移、截面扭转角以及2#墩中间支座竖向支反力的影响情况。

图9 车辆行驶速度对曲线桥响应的影响

由图9可以看出：速度对跨中竖向位移的影响很小，但是对跨中的横向位移、扭转角及2#墩中支座的竖向支反力均有较大影响，它们随着速度的增加而增加。

表7中具体列出了不同速度对应的各响应的峰值及其随速度增加的增长率。

表7 不同速度下各响应的峰值及其增长率

从表7中可以看出，随着速度的增加，不仅各个响应的最大值在增加，增长速率也在增大，其中横向位移的增长率最大，说明速度对横向位移的影响最大。

3.3 载重的影响

载重分别为20 t、25 t、30 t的车辆均以15 km/h的速度通过曲线桥时，第二跨跨中中腹板下(B点处)的竖向位移、横向位移和跨中截面扭转角及2#墩中支座竖向支反力随载重的改变而改变的趋势如图10所示。

图10 车辆载重对曲线桥响应的影响

由图10可以看出：载重对竖向位移、横向位移、截面扭转角和支反力都有很大的影响。相较于偏载和速度，载重对曲线桥竖向位移、横向位移、截面扭转角和支反力的影响更加显著。表8和表9分别列出了各个响应在不同载重下的正向峰值和负向峰值以及它们随载重增加的差值。由表8和表9中可以看出，载重的增加不仅使各个响应的正向峰值变大，还使得其负向峰值有所增加。增加相同的载重，差值的增加基本相同。

表8 不同载重下各响应的正向峰值与其随载重增加的差值

表9 不同载重下各响应的负向峰值与其随载重增加的差值

4 材料非线性对曲线桥动力响应的影响

采用图5的本构关系，计算了载重分别为20 t、30 t、40 t、50 t、60 t的汽车以15 km/h的速度行驶下曲线桥动态响应，并将结果与线弹性材料计算模型的响应进行对比。图11为荷载为60 t时，曲线桥模型分别采用非线性材料与线性材料对曲线桥跨中竖向位移、横向位移、截面扭转角和2#墩中支座竖向支反力的影响情况。

图11 材料非线性对曲线桥动态响应的影响

从图11中可以得出，材料非线性对支反力影响很小。从图11(a)～图11(c)可以看出，虽然材料的非线性对竖向位移、横向位移和扭转角有一定影响，但是仅仅使峰值有所增加。从图5本构关系可以看出，随着应力的增大，对应的非弹性应变也越大，反映到图11可以得出，当荷载经过跨中位置时，跨中截面应力最大，从而引起位移和扭转角峰值的增加。

表10、表11和表12分别列出了不同汽车载重作用下材料非线性对第二跨跨中截面最大竖向位移、最大横向位移和截面扭转角的影响情况。为了观察材料非线性对最大位移的影响随载重的变化情况，图12展示了偏差值随载重增加的变化曲线。

表10 材料非线性对第二跨跨中最大竖向位移的影响 mm

表11 材料非线性对第二跨跨中最大横向位移的影响 mm

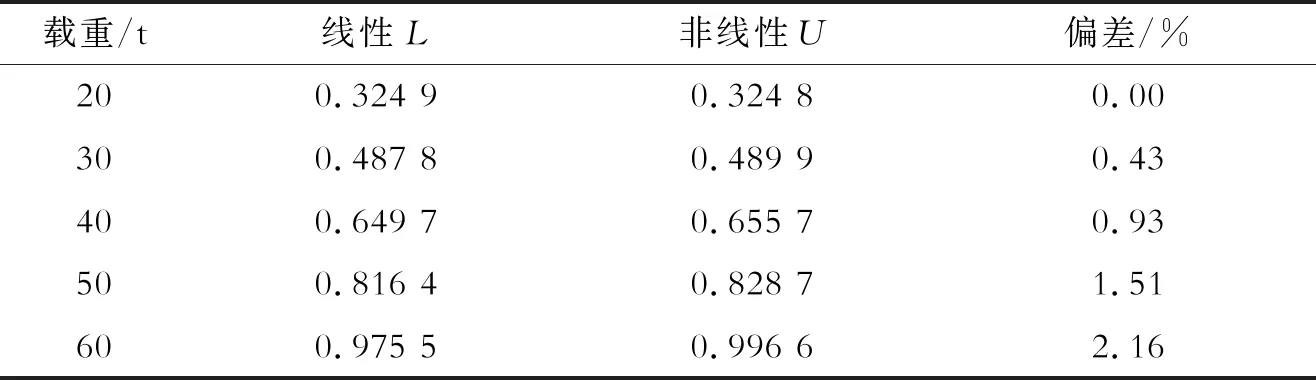
表12 材料非线性对第二跨跨中截面扭转角的影响 10-3(°)

图12 偏差随载重的变化曲线

由表10、表11和表12可以看出：随着载重的增大，第二跨跨中最大竖向位移、横向位移和扭转角都在不断增大。而且随着载重的增大，最大竖向位移的偏差由0.24%增大到2.32%，最大横向位移的偏差由0.11%增大到2.45%，最大扭转角的偏差由0增大到2.16%。从图12可以看出：随着荷载的增加，3种响应的偏差曲线逐渐变陡，说明随着移动荷载的增加非线性作用越来越明显。但是走势基本保持直线，说明该桥在正常车辆行驶状态下非线性作用并不明显。

5 结论

(1)车辆偏载对曲线桥的动力响应影响较大，由于“弯扭耦合”作用的存在，车辆沿外侧行驶时引起的动力响应最大。

(2)车速对跨中竖向位移的影响很小，但是对跨中的横向位移、扭转角及支座的竖向反力均有较大影响。

(3)载重对曲线桥动力响应的影响很大，使各个响应的正向峰值和负向峰值均有所增加。

(4)材料非线性因素对支反力影响很小，但是会使跨中竖向位移、横向位移及扭转角的峰值略有增加，随着载重的增加非线性作用越明显。