制动工况下未知路面附着特性识别方法
霍肖楠, 冯国胜, 应 铭, 贾素梅
(1.石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043;2.石家庄铁道大学 机械工程学院,河北 石家庄 050043)
近年来国内汽车数量呈爆发式增长。为了提高道路交通的安全性,汽车制动的相关技术研究已经成为关键问题[1]。
在汽车防抱死制动过程中,车轮角速度变化量由地面制动力、车轮制动力矩、车轮滚动半径等共同决定,而路面附着系数与整车质量决定了地面制动力的大小,因此路面附着系数是制动控制系统中的一项重要参数。在汽车防抱死制动控制系统的建模中,往往将一条已知的典型路面附着系数特性曲线建立在模型中,根据线性查表或现有的轮胎-路面模型得到车轮滑移率与附着系数的对应关系,将目标滑移率控制在15%~20%[2-4],在研究中默认车辆行驶过程中所行驶路面的附着特性关系均是已知的。实际车辆行驶的路面环境会由于温湿度、粗糙度及材料等因素的变化使附着特性发生改变,改变后的路面附着特性往往是未知的或非典型的,典型已知路面的附着特性关系在未知路面中的制动控制模型中将不再适用。及时对未知路面附着特性进行有效识别可根据当前路面进一步锁定最佳滑移率,同时对制动器制动力进行调整,取得更好的制动效果[5-6]。
目前针对路面附着特性识别方法的研究大致分为2类[7]:基于原因和基于效应。文献[8]采用基于轮缸压力的附着系数估算方法;文献[9]采用基于激光雷达的路面附着系数估计方法;文献[10]通过模型峰值确定滑移率与峰值附着系数;文献[11]采用典型路面附着系数平均法对未知路面峰值附着系数进行估算。本文的识别算法属于基于效应,利用常用的轮速传感器、车速传感器等设备,根据不同瞬时车况下的滑移率与附着系数信息,选取适宜的单边或双边典型参考路面,分别结合线性类比以及权重分配思想,对未知路面峰值附着系数与抱死附着系数进行估算,进而根据路面通用附着特性对当前路面整体附着特性曲线进行识别。
1 典型路面轮胎-地面模型
对于路面附着特性目前大多采用双线性模型、Burckhardt模型以及“魔术公式”模型来描述滑移率与附着系数的关系。选用拟合精度较高、参数较少的Burckhardt模型为基本参考数据,对轮胎地面附着特性进行研究[12]。Burckhardt模型公式为
φ(s)=c1(1-ec2s)-c3s
(1)
Burckhardt模型归纳出了7种典型路面的曲线模型系数,7种典型路面的Burckhardt模型参数见表1。

图1 Burckhardt模型下的典型路面附着特性曲线
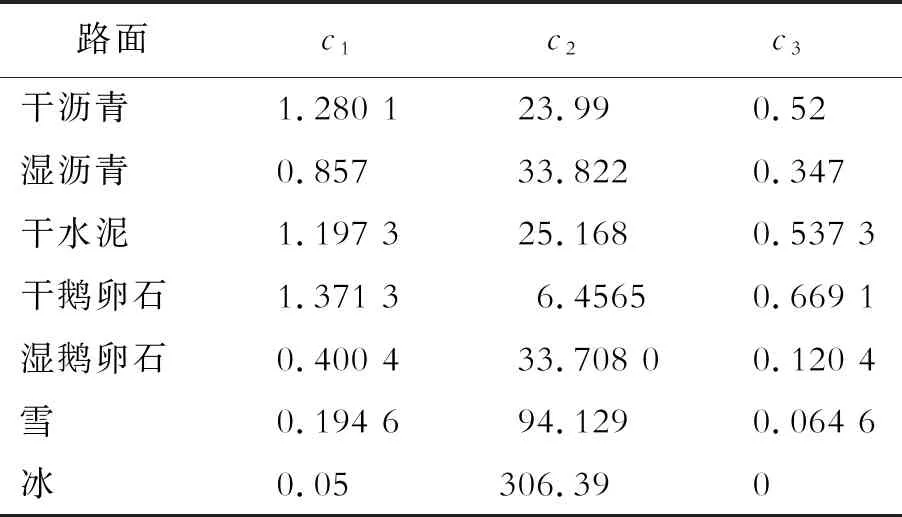
表1 7种典型路面的Burckhardt模型参数
在Burckhardt模型中,仅需要获知3个参数就可对任意路面进行滑移率与附着系数关系的描述,Burckhardt模型下的典型路面附着特性曲线如图1所示。
由图1可知,各种不同类型路面的滑移率与附着系数关系呈现出相似的变化趋势:路面附着系数首先随着滑移率的增大而增大,达到路面峰值附着系数,此时的滑移率为最佳滑移率,随后路面附着系数又随着滑移率的增大而减小,直到滑移率为100%时达到抱死附着系数。然而不同的路面在相同滑移率下的附着系数各不相同。其中,干鹅卵石路面的附着特性与其他路面差异较大,不满足大多数路面的类比统一规律,因此,干鹅卵石路面不作为路面识别的典型参考路面。7种典型路面附着特性参数见表2。

表2 7种典型路面附着特性参数
由表2可知,在不同路面附着特性导致了最佳滑移率不同。车辆制动控制系统需实时对当前路面附着特性进行识别,根据路面特性状况确定车轮的最佳滑移率,然后通过调节车轮制动压力,使实际车轮滑移率保持在最佳值附近[13]。
2 路面附着特性参数采集与估算
2.1 瞬时车况下路面附着数据采集
汽车的制动控制要求具有很好的实时性,路面附着特性的识别是制动控制的前提,路面附着特性的识别方法应该满足快速、准确以及高效。在瞬时状态下,单个车轮的滑移率与路面附着系数的值是唯一的。根据传感器实时获取到的轮速与车速信息,可计算得到瞬时状态下的滑移率
(2)
式中,v为车速;ω为车轮角速度;r为车轮滚动半径。
路面附着系数被定义为地面纵向力与垂直载荷的比值。地面纵向力可由车辆所受加速度的大小计算得到。为了减少数据运算与处理的时间,采用基于地面制动减速度的路面附着系数计算方法来获取瞬时状态下路面的单一附着系数[14]。
(3)
式中,Fxb为地面制动力;FZ为车轮垂直载荷;g为重力加速度;Δv为相邻2次采样车速差;Δt为车速采样周期。
由此,车辆电控单元可通过车载传感器装置获取自车车速、轮速信息,经过计算得到瞬时状态下路面附着系数与滑移率对应关系的一组真实数据点。
2.2 未知路面的附着系数估算方法
由于各路面的附着系数特性曲线具有相似的变化趋势,因此,可利用与未知路面附着特性相近的已知典型路面附着特性曲线,对未知路面的抱死附着系数、峰值附着系数以及最佳滑移率等数据点进行估算。
某一时刻下车辆获得未知路面的瞬时附着特性参数(se,φe),将滑移率为se时其他典型路面的附着系数与φe进行对比,选出1条或2条与未知路面附着特性曲线最相近的典型路面作为参考路面,参考路面选取示意图如图2所示。当未知路面附着特性曲线高于或低于所有典型路面时,仅选取1条最近典型路面作为单边参考路面即可,如图2(a)所示;当位置路面附着特性介于2条典型路面之间时,选取其上下2条最近的典型路面作为双边参考路面,如图2(b)所示。

图2 参考路面选取示意图
假如通过相同滑移率下的附着系数大小比较获知:相同滑移率下,未知路面附着系数最小,且与典型路面A的附着系数最为相近,应选取单边参考路面。基于线性类比的思想,利用典型路面A的曲线数据对未知路面的峰值附着系数和以及抱死附着系数进行估算,认为未知路面附着特性与典型路面A具有以下线性关系
(4)
式中,φAp为典型路面A的峰值附着系数;φep为未知路面的峰值附着系数;φAl为典型路面A的抱死附着系数;φel为未知路面的抱死附着系数;φAe为滑移率为se时典型路面A的附着系数。
同理,未知路面的最佳滑移率也可根据典型路面A的最佳滑移率进行线性估算
(5)
式中,sAr为典型路面A的最佳滑移率;ser为未知路面的最佳滑移率。
假如通过相同滑移率下的附着系数大小比较获知:未知路面附着系数介于典型路面A与典型路面B两者之间,其中典型路面A的附着系数较高,典型路面B的附着系数最低,选取双边参考路面,基于权重分配的类比思想,利用典型路面A与典型路面B的曲线数据对未知路面的峰值附着系数和抱死附着系数进行估算
(6)
(7)
式中,φBe为滑移率为se时典型路面B的附着系数;φBp为典型路面B的峰值附着系数;φBl为典型路面B的抱死附着系数。
同理,未知路面的最佳滑移率可在双边参考路面下根据路面A与路面B的最佳滑移率进行估算
(8)
式中,sBr为典型路面B的最佳滑移率。
对于可以选择双边参考路面计算的未知路面,也可使用单边参考路面进行计算,但经过对比发现,选用单边参考路面预测出的数值结果误差比采用双边大。
2.3 附着系数估算结果误差分析
附着系数特性曲线识别的关键问题首先在于峰值附着系数与抱死附着系数估算的准确性,其次是利用数据组对曲线拟合的拟合算法。由上文可知,汽车在同一路面行驶中,滑移率与附着系数的采样数据不同,其估算结果也会有所差异。

图3 干水泥路面峰值、抱死附着系数估算结果
使用一条已知的典型湿沥青路面作为未知路面,使用该路面附着特性曲线的所有数据点对该路面附着特性曲线的峰值附着系数与抱死附着系数进行估算,将估算结果与Burckhardt模型下的该路面峰值附着系数与抱死附着系数进行对比,根据误差分析结果验证算法的可靠性。
由图1中各路面附着关系可知,干水泥路面附着特性介于干沥青与湿沥青之间,故选用双边参考路面算法对湿沥青路面峰值附着系数与抱死附着系数进行估算,估算结果如图3所示。
由图3可知,干水泥路面估算峰值附着系数的最大值为1.092 7,最小值为1.024 3,估算抱死附着系数的最大值为0.707 0,最小值为0.659 9。表2中干水泥路面的峰值附着系数为1.090 0,抱死附着系数为0.660 0。结果表明,干水泥峰值附着系数的估算最大误差约为6%,抱死附着系数的估算最大误差约为7.1%。
3 未知路面附着特性曲线拟合与验证
使用已知典型路面作为未知路面,将识别结果与Burckhardt模型下的该路面附着特性曲线进行对比,根据误差分析结果验证识别算法的可靠性。
假设车辆瞬时状态下获取干沥青路面、湿沥青路面、干水泥路面、干鹅卵石路面、湿鹅卵石路面、雪路面以及冰路面的滑移率-附着系数分别为(0.6,0.968 1)、(0.6,0.648 8)、(0.6,0.874 9)、(0.6,0.941 3)、(0.6,0.328 2)、(0.6,0.155 8)、(0.6,0.05),分别根据其适宜的参考路面进行相关附着特性参数的估算。其中,干沥青与冰路面选用单边参考路面,其余路面选用双边参考路面。根据上述瞬时数据,对7种典型路面附着特性参数进行估算,估算结果如表3所示。
由图1路面附着特性曲线可知,各路面的附着特性曲线恒过(0,0)点,因此可获得未知路面附着特性曲线中的4组数据点(0,0),(ser,φep),(se,φc),(1,φel)。
根据曲线坐标可知,所得4组数据点处于附着特性曲线的关键节点处,对附着曲线具有较好的拟合性。为了得到完整的路面附着系数特性曲线,在Matlab中分别对识别路面附着特性曲线进行非线性拟合,7种典型路面识别结果如图4所示。

表3 7种典型路面附着特性参数估算结果

图4 7种典型路面附着特性曲线识别结果
由图4可以看出,干鹅卵石路面与其他典型路面特性的差异性较大,在识别结果中存在较大误差。其余6种典型附着特性曲线的识别结果与Burckhardt模型中的相似,具有相同的滑移率与附着系数关系,得到了较好的拟合结果。
4 结论
为了加强未知路面识别的实时性与可靠性,提出了使用瞬时车况数据对路面附着特性的识别算法,实现了车辆对当下路面附着特性进行快速识别。首先,利用单个实际路面附着特性数据,对该路面的峰值附着系数与抱死附着系数进行估算,经过对比,峰值附着系数估算结果的最大误差约为6%,抱死附着系数误差最大约7%;随后,结合路面附着特性的特点,利用4组数据对路面附着特性进行拟合,经过与Burckhardt模型进行比较,验证了该方法在多数路面附着特性识别中具有较好的可靠性。

