含储能系统的区域电网快速调频控制策略
周 丹,童 伟,汪 蕾,刘业伟,楼伯良,马骏超
(1.浙江工业大学 信息工程学院,浙江 杭州 310023;2.国网浙江省电力公司电力科学研究院 电网中心,浙江 杭州 310006)
大规模可再生能源并网以及充电桩的大量使用,导致发电侧和负荷侧在时间和空间上不匹配,造成不可忽略的频率波动,严重影响了电力系统的稳定运行[1-2]。传统的调频方式由于响应速度慢,无法达到现代电力系统快速调频的要求,因此需要在现有调频方式的基础上增加一种新的调频手段来及时平抑频率波动。储能系统作为辅助电网调频的设备之一,具有响应速度快、技术成熟和经济适中的特点,已得到大规模应用。电网中出现负荷需求功率与发电功率不平衡会导致电网中的频率发生改变,而储能系统能够快速响应并向电网释放或吸收功率,辅助电力系统及时调整使得功率达到平衡状态,进而使电网频率保持稳定。因此,在新能源高渗透的电力系统中,储能系统能够有效地改善和提高电力系统的频率调节能力[3]。
近年来,很多学者针对储能系统参与电网快速调频开展了大量的研究。文献[4-5]提出利用电动汽车移动储能来辅助电网调频,其中文献[4]提出了基于SOB(State of battery)排序的频率控制策略,仿真结果表明:该方法不仅能够有效平抑电网频率波动,而且能够满足人们日常出行需求。文献[6-8]考虑风电的不确定性,通过风-储的协同配合使系统自身频率保持稳定。文献[9-10]提出了功率型和能量型混合的储能控制方法,其中文献[9]考虑储能的充放电速率和容量大小以蓄电池和电容器作为补偿设备,仿真结果表明:经补偿后系统输出的有功功率能够保持在误差范围内。文献[11]提出了鲁棒控制策略,用于减少带有附加存储的智能微电网系统中由负载波动和可再生资源引起的系统频率偏差。文献[12-13]提出了一种混合储能系统的自适应能量管理控制策略来控制储能的出力大小,结果表明所研究策略能够合理控制储能出力且有效改善电网的抗干扰能力。文献[14]考虑电网频差限度来控制储能系统输出有功功率的大小,但是仅考虑在系统频率死区内调整储能的荷电状态,没有综合考虑整个系统的运行情况对储能出力大小的约束,文献[15]在文献[14]的基础上综合考虑整个系统的运行情况并提出了综合控制策略,确定了储能在不同时间点输出功率的大小及时机,提高了储能和发电机组之间的运行效率。文献[16-18]综合考虑了电力系统调频需要的功率值,通过调节储能出力的大小,合理分配一、二次调频的需求,有效改善电网频率质量。上述文献,虽然提出了多种控制策略并解决了储能投入和退出调频运行状态的时刻以及参与调频的出力大小,但是很少有文献针对电网的调频特性进行分析建模,进而准确地设定储能系统的调频控制参数。笔者对储能系统辅助区域电网一次调频进行分析,首先,建立含储能系统的区域电网模型并推导出其传递函数;其次,根据传递函数进行幅频特性分析,在此基础上提出含储能系统的区域电网控制策略并推导出储能系统的调频控制参数;最后,利用仿真结果验证所提控制策略的有效性。
1 含储能系统的区域电网模型
1.1 常规区域电网的一次调频模型
电力系统调频由汽轮机、调速器、负荷扰动模型以及其他输入模型等环节组成[19],如图1所示。建立常规区域电网动态的一次调频模型,如图2所示。
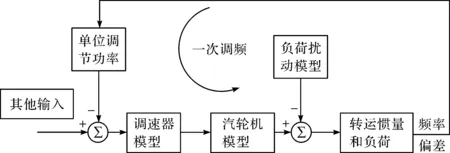
图1 常规区域电网的一次调频模型

图2 常规区域电网动态的一次调频模型
图2中:D为负荷阻尼的系数;M为电力系统惯性时间常数;KG为传统电源的单位功率调节系数;TG为机组调速器时间常数;TCH,TRH,FHP分别为汽轮机时间常数、再热器时间常数、再热器增益;ΔPg为常规机组有功变化值;ΔPL为负荷波动。根据图2可得出一次调频的传递函数Gf1(s)为
(1)
其中
(2)
1.2 含储能系统的域电网等效模型
对于储能系统参与电力系统调频,结合工程实际需求,一般将电池储能近似等效成一阶惯性环节和比例环节的串联[20],传递函数为
(3)
式中:Kb为储能系统的单位调节功率;Tb为时间常数,Tb的取值与电池的材料有很大的关联,不同材料的电池其时间常数也不同,笔者采用磷酸铁锂电池作为储能电池,其时间常数Tb为0.2 s。
储能系统辅助调频的过程中,一般将频率偏差Δf作为控制信号,而输出信号为储能系统参与调频出力的大小,将储能模型并入区域电网动态模型[12]中,如图3所示。根据图3调频模型,得出一次调频的传递函数Gf2(s)为
(4)
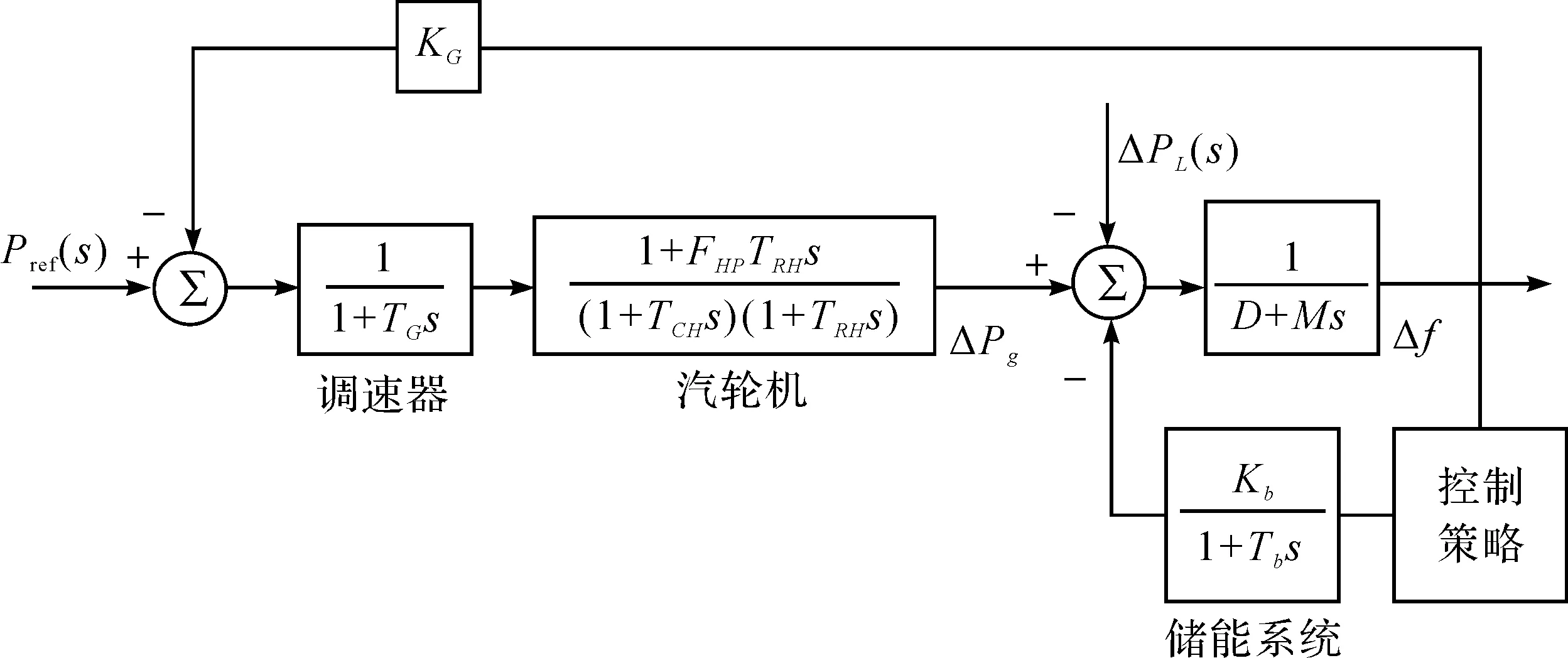
图3 储能辅助一次调频的区域电网等效模型
2 含储能系统的区域电网幅频特性分析
笔者在频域中分析负载扰动对含有储能的区域电网频率的影响程度,通过其传递函数得出幅频特性,在此基础上研究区域电网模型频率的变化,进而分析含储能系统和负载扰动的区域电网频率特性,根据图3,假设Pref(s)=0,那么在ΔPL(s)作用下系统的开环传递函数为
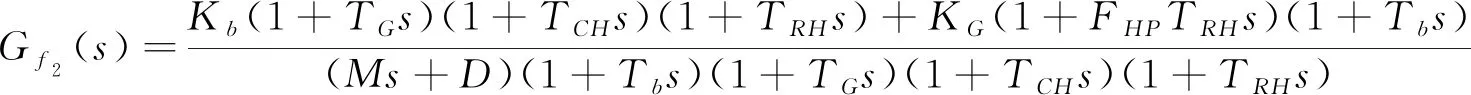
(5)
其频率特性Gf2(jω)的分子为
(Kb+KG-Kb(TCHTRH+TGTRH+TGTCH+KGFHPTRHTb)ω2+j((Kb(TRH+TCH+TG)+
KGTb+KGFHPTRH)ω-KbTGTCHTRHω3)
(6)
分母为
D+(M(TG+TRH+TCH+Tb)+D(TCHTRH+TbTG)+(TG+Tb)(TCH+TRH))ω2+(TbTRH(M(TG+TCH)+DTGTCH)+MTCH(TGTRH+TbTG)ω4+j((M+D(TRH+TG+Tb)+TCHD)ω-((TGTb+TbTRH+TGTRH)(TCHD+M)+TCH(M(TRH+TG+Tb)+DTbTGTRH))ω3+TCHTGTRHTbMω5)
(7)
现令
(8)
则Gf2(jω)可以表示为
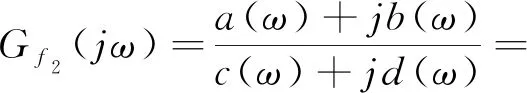
(9)
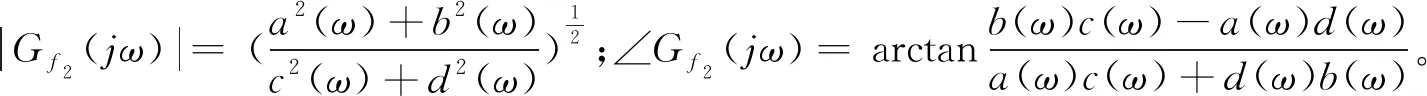
相位裕度γ和幅值裕度Kg表达式为
γ=180°+∠Gf2(jωc)
(10)
(11)
式中:ωc为截至频率;ωg为相位穿越频率。使得
(12)
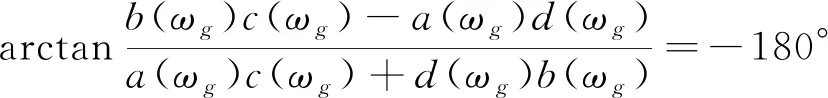
(13)
根据式(12,13)可得系统处于稳定状态的临界条件,同时可根据Gf2(s)的根轨迹分布情况来验证系统是否稳定。
3 含储能系统的区域电网调频的控制策略及参数整定
储能辅助区域电网进行一次调频时,储能系统可以把由负载扰动引起的频率偏差转化为储能输出功率的大小。将负载扰动产生的频率偏差看作是多个周期、幅值不同的阶跃量的叠加,把其作为储能系统的输入,而储能系统的输出则具备线性定常系统的特征。基于此,笔者采用PID控制方法来研究储能系统提高区域电网快速调频的有效性。
PID控制的储能系统输入输出关系式为
(14)
根据式(5)简化可得此系统为5阶系统,针对高阶系统难以准确地求解,有学者提出了PADE降阶法[19],该方法虽然会产生系统偏差,但是它能够将高阶系统转化为便于求解的低阶系统,并且能够一定程度上保持原先系统的特征。因此,对此系统利用PADE降阶法进行降阶处理。设(m,n)阶系统传递函数为
c0+c1s+c2s2+…+cnsm
(15)
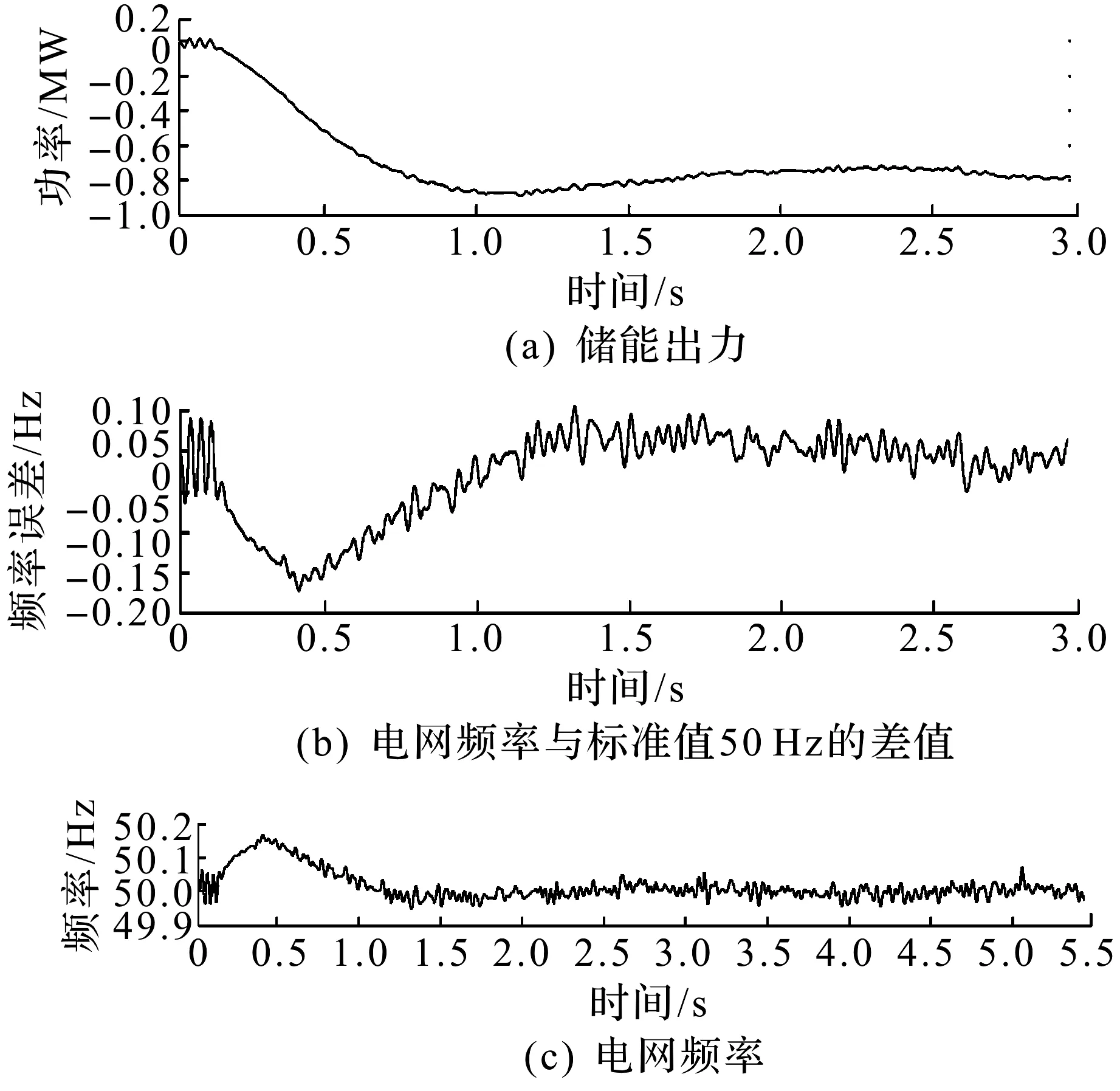
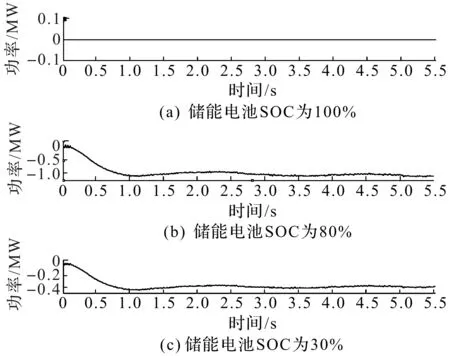
若存在一个(j,k)阶系统(j (16) 且有ci=ri(i=0,1,…,j+k),则称R(s)为G(s)的(j,k)阶PADE迫近。 将式(15,16)展开,比较其系数可得 (17) 其中 (18) 由式(18)可得降阶后的二阶系统传递函数为 (19) 对此传递函数进行PID控制,选定闭环极点参数为 (20) 则PID参数为 (21) (22) 加入积分控制,这相当于系统增加为三阶,可取另一闭环极点在负实轴上,得到 λ3=-mξiωni (23) (24) 式中m属于任意常数,其值可影响系统超调量和进入稳态的时间。 用配置极点的方法决定PID参数,ξ的变化范围是受到约束的,由于PID参数Td,Ti必须是正值,因此其变化范围为 (25) 方案采用IEEE33节点电网,搭建系统仿真模型如图4所示。该系统中设置3 个电池储能,并设置图3中各参数值,其中负荷阻尼的系数D为电网中所有负荷阻尼系数之和;电力系统惯性时间常数M为电网中所有发电机时间常数之和的2倍;单位功率调节系数KG和再热器增益FHP,其标幺值分别为1,5,20,0.5;TG,TCH,TRH值分别为0.1,0.3,10 s。 图4 含储能系统的区域电网仿真图 根据式(4)在Matlab中得出其闭环传递函数为 (26) 画出其根轨迹,如图5所示。 图5 高阶系统根轨迹 由图5可知:该系统处于稳定状态且系统的性能指标可由主导极点替代系统全部闭环极点来估算,主导极点可取-1.93±4.5i,阻尼比为0.393,超调量为26.1%。负荷扰动作用时,系统的传递函数如式(5)所示,根据式(17~19)可得降阶后系统的传递函数为 (27) 根轨迹如图6所示,系统处于不稳定状态,在此基础利用PID进行调节,根据式(21~25),取ξ=0.7,并且通过不断调试后取最优的一组数据,则KP=0.2,KD=1.6,KI=1.34。经调节后的系统的传递函数为 (28) 图6 降阶后系统根轨迹 调节后的系统其根轨迹如图7所示。经过调节后系统保持稳定状态,并且随着其增益的不断增加系统能够达到最佳阻尼比,对比图5超调量也有大幅的减小,有效地提高了系统的暂态性能。 图7 PID调节后系统根轨迹 4.3.1 第1组数据设置 节点32接入0 kW负荷,SOC的容量为100%,系统的运行情况如图8所示。由图8可知:节点32接入0 kW负荷,由于电网中只存发电机调速器,电网频率在50 Hz上下波动。 图8 当接入负荷为0 kW时系统的运行情况 4.3.2 第2组数据设置 节点32接入1 200 kW负荷,SOC的容量为100%,利用笔者的调频控制策略,系统的运行情况如图9所示。由图9可知:在增加负载至1 200 kW的情况下,由于电网中只存在发电机调速器,频率下降稳定在49.9 Hz左右,利用笔者的频率控制策略,经过1 s左右可以把频率调回50 Hz。 图9 当接入负荷为1 200 kW时系统的运行情况 4.3.3 第3组数据设置 节点32接入1 200 kW;一号储能的SOC容量设置为30%;2,3号储能的SOC容量均设置100%。利用笔者的调频控制策略,系统的运行情况如图10所示。由图10可知:增加负载至 1 200 kW,一号储能的SOC为30%,处于较低的水平,2,3号储能的SOC均为100%。利用笔者的频率控制策略,系统的运行频率仍然能够稳定地保持在50 Hz左右。 图10 负荷为1 200 kW,第1个SOC为30%时系统的运行情况 3 个储能系统出力分别如图11所示。在储能系统SOC不足时会提高要求储能系统的总数,同时3 个储能系统出力分配也不同,SOC较低的储能系统会根据所定标准进行出力,至11 s左右第1个储能系统的SOC降低到30%以下,停止放电。所减小的功率输出数目则由其他两个正常的储能系统承担,既保证了电网调频目标的完成,也有效防止了储能系统过放损伤电池寿命。 图11 3 个储能系统出力情况 4.3.4 第4组数据设置 1号储能系统SOC为30%;2号储能SOC为80%;3号储能SOC为100%。因为单一节点负载减小时对电网影响有限,则选择30, 31, 32 节点负荷置0 kW。利用笔者的调频控制策略,系统的运行情况如图12所示。由图12可知:由于单一节点负载减小,选择30,31,32 节点负荷置0 kW,1号储能和2号储能进行工作。利用笔者的频率控制策略,系统的运行频率经过1 s稳定地保持在50 Hz左右。 图12 第1个SOC为30%,第2个SOC为80%时系统运行情况 3 个储能系统出力如图13所示,3 个储能系统出力分配也不同,当SOC为100%的储能系统停止充电,所减小的功率输出数目则由其他两个正常的储能系统承担,其中SOC为30%的储能系统会根据所定标准增大吸收功率,同时SOC为80%的储能系统配合SOC为30%的储能系统进行功率调节,这样既保证了电网调频目标的完成,也有效防止了储能系统过放损伤电池寿命。 图13 3 个储能系统出力情况 仿真时3 个储能系统分别处于完全不充电、充电受限制和正常充电的情况。在调频效果方面,笔者提出的调频控制策略在调频速度和稳定性上效果都较好。单个SOC的限制,并不影响储能系统整体的调频效果,原因是SOC较高的储能系统减少从电网中吸收电能,这一部分电能由正常储能系统承担。 针对现阶段电力系统一次调频能力减弱的趋势,笔者提出了含储能系统的区域电网快速调频控制策略。通过对电网的调频特性进行分析建模,推导出储能系统的调频控制参数,并得出以下结论:1) 储能系统参与电网调频能够有效地提高电网抗干扰能力;2) 通过理论分析得出的控制参数能够较好地对负载扰动作出快速响应并且能够保持系统的稳定;3) 算例仿真结果表明,储能系统参与电网频率的调节时效果良好,负载在一定范围内变化时,通过增减储能系统的出力均可完成调频,且使用笔者提出的调频控制策略在1 s内就可完成调频任务,控制效果比较理想。由于电网中存在着很多在建模时难以用准确数学公式来描述的不确定性因素,并且在使用PADE法降阶时会存在一定的误差,因此如何减小理论值与实际控制效果的偏差,是笔者进一步研究的方向。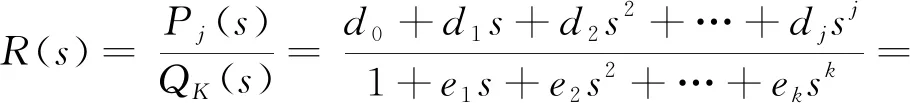
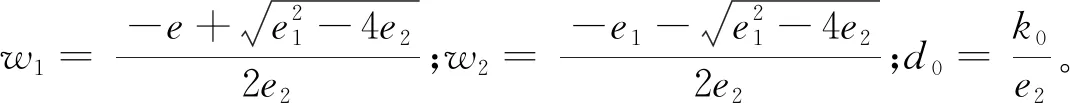
4 算例验证
4.1 仿真参数设置
4.2 调频策略及参数整定

4.3 仿真结果及分析
5 结 论

