新型单箱砼-多钢箱混合梁桥结构冲击系数研究

戴 飞，冯伟杰，陈光军，彭卫兵

(1.浙江工业大学 土木工程学院，浙江 杭州 310023；2.浙江长兴县交通投资集团，浙江 湖州 313100)

对于跨平原湖泊地区桥梁来说，由于桥下通航高度的要求，中等跨径混合梁桥由于降低了主梁截面高度而得到广泛应用。混合梁中的整体钢箱梁多采用分箱制作，运到现场后进行连接，因此现场焊接工作量大，施工进度慢。同时由于钢箱梁梁高一般设置较小，工人在整体箱梁中焊接施工不方便，箱内焊接难度较大且施工质量不易保证。针对上述问题，笔者将单箱多室钢箱梁变为多箱单室即分离式钢箱梁，通过设置钢横隔梁并采用螺栓连接将各分离钢箱梁连接成整体，混合梁形式转化为多箱单室钢箱梁与单箱多室混凝土箱梁连接，大幅度的减少箱内焊接的工程量，从而保留混合梁自重低的优点，并降低施工难度，提高施工效率，以此探索适合跨平原湖泊地区中等跨径混合梁桥适宜形式。混合梁的出现，解决了纯混凝土梁在长期荷载作用下的跨中下挠问题，也解决了单纯采用钢主梁存在的支座附近箱梁钢底板和腹板厚度过厚的问题[1]。目前,国内外对混合梁的使用性能研究主要集中在其抗震性能上[2-5]，因而正确评估单箱砼-多箱钢混合梁桥这一形式混合梁桥的整体动态性能影响显得尤为重要。

混合梁动力性能评价指标主要为车桥耦合作用下的冲击系数变化。张哲等[6]以弯塔混合梁斜拉桥为研究对象，利用白噪声作为激励源进行了缩尺模型自振频率及振型测试，并使用ANSYS建立空间有限元模型，对比分析相应形式的斜拉桥直塔和混凝土加劲梁动力特性。王凡[7]以铁路混合梁斜拉桥——宁波甬江大桥为工程背景，建立列车-桥梁时变系统整体振动有限元模型，分别进行了3 种国产高速列车下的车桥耦合振动分析，并研究车辆系统行驶速度、结构体系、结合段位置及辅助墩数量对桥梁和车辆动力响应的影响。赵玉等[8]总结了车桥耦合振动分析方法及车辆运动学模型振动方程的建立，并以某跨径布置为(84 m+200 m+84 m)的混合梁刚构桥为对象，建立有限元模型，计算车重、车速、桥面平整度及钢梁断长度对桥梁跨中冲击系数的影响。焦伟立[9]针对渭河特大桥，建立了10种不同的刚度配置方案，进行重车作用下桥梁时程和频谱分析，对桥梁行车平顺性进行评价。赵航[10]及沈佩文[11]分别以金溪大桥为对象，通过有ABAQUS有限元软件及现场动力试验研究了该新型新型单箱砼-多钢箱混合梁桥的结构性能。高庆飞等[12]结合理论推导与仿真模拟,并考虑其物理意义,对不同情况下的梁桥冲击系数进行了详细讨论，并对多跨连续梁的动力性能做出了一定评价。笔者通过使用ABAQUS非线性动力学模块，计算移动车辆以不同车速、不同轴重行驶时的桥梁动力响应，并以长兴金溪大桥为研究案例，以边跨混凝土箱梁及中跨钢箱梁边钢箱及中钢箱竖向位移为对象，计算其位移冲击系数，并与规范进行对比，分析该形式桥梁的整体动力性能。

1 工程背景

长兴金溪大桥上跨长湖申线航道，桥梁轴线与航道轴线交角为88.2°，桥下最高通航水位2.86 m，通航净空为宽55 m×高7 m。桥梁总宽38 m，采用左右幅分离设计，主桥上部结构采用(45 m+80 m+45 m)钢-混混合梁，其立面图如图1所示。

图1 金溪大桥立面图

主桥混凝土箱梁采用单箱三室断面设计，箱梁顶面宽18.75 m，挑臂长为2.5 m，底面宽13.75 m。主墩顶部混凝土箱梁部分断面梁高为4.5 m，中跨混凝土箱梁断面梁高1.6 m，边跨梁端箱梁断面梁高1.7 m，其间梁底下缘高度以二次抛物线变化；箱梁顶板厚为25 cm，箱梁底板根部厚为160 cm，边跨混凝土箱梁底板厚为25 cm，中跨混凝土箱梁底板厚为35 cm，其间各段箱梁底板厚度按二次抛物线变化；边跨箱梁腹板厚度为50 cm，腹板厚度沿桥纵向渐变，跨中6 m部分腹板厚度为70 cm，中跨箱梁腹板厚度为70 cm，与钢箱梁相邻4.5 m范围内混凝土箱梁腹板厚度渐变为100 cm。综合考虑主桥主墩及交接墩部分混凝土箱梁的受力和变形要求，在该部分混凝土箱梁内设置横隔梁。

主桥钢箱梁长40 m，钢箱梁断面同混凝土箱梁主跨跨中断面宽度一致，采用四箱单室设计，钢箱梁顶面总宽为18.75 m，挑臂长为2.5 m，钢箱梁底总宽为13.79 m。横向沿桥纵方向每1.5 m设置一道横隔板，其中大横隔板和小横隔板交替设置，各箱室之间的横隔板采用螺栓连接；同时为了增加钢箱梁的结构刚度，于钢箱梁内部顶、底板处设置纵向加劲肋。

2 有限元模型建立

2.1 车辆模型

依据文献[13]选用标准55 t三轴车辆模型，车辆空间模型如图2所示。车辆空间模型将车划分成11个集中质量，分别为1个车体和10个车轮，并将车悬架质量集中到车轮上。其中车体与车轮，车轮与桥面之间连接件简化为弹簧—阻尼系统，从而将车辆简化为由集中质量、弹簧和阻尼系统组成的三维体系。

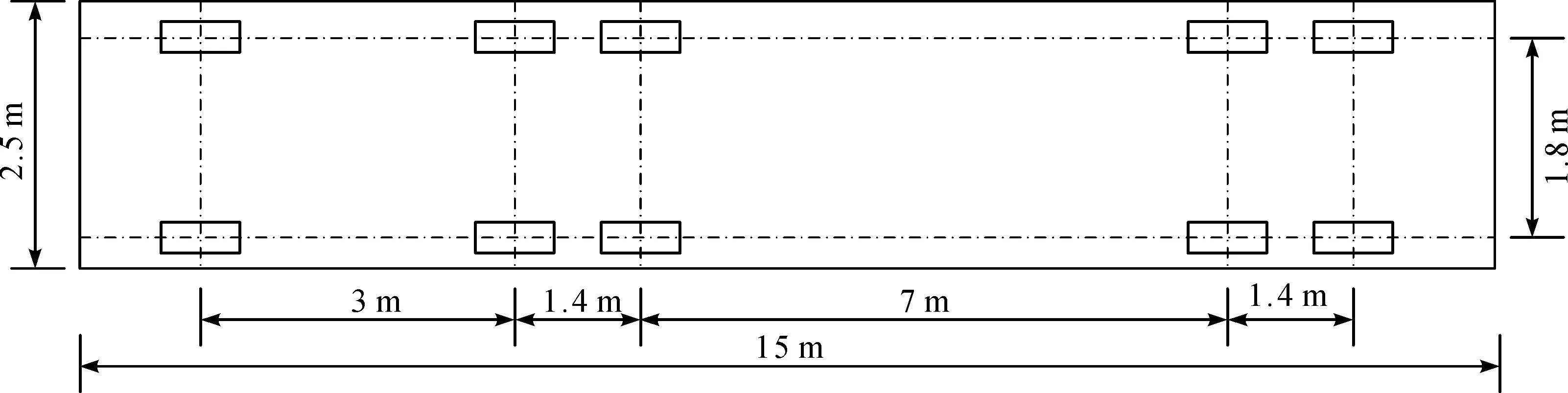
图2 规范55 t标准车辆

车辆模型组成如图3所示，车辆模型参数如表1所示，其中M1+M2为车体质量；m1～m2为前轮的质量(包含车悬架质量)；m3～m10为中后轮的质量，k11～k110,c11～c110分别为车悬架刚度和阻尼；k21～k210,c21～c210分别为轮胎的刚度和阻尼。模型考虑了10 个车轮的竖向位移、车体的竖向位移、车体的俯仰角位移和车体的侧倾角位移，共13 个自由度。

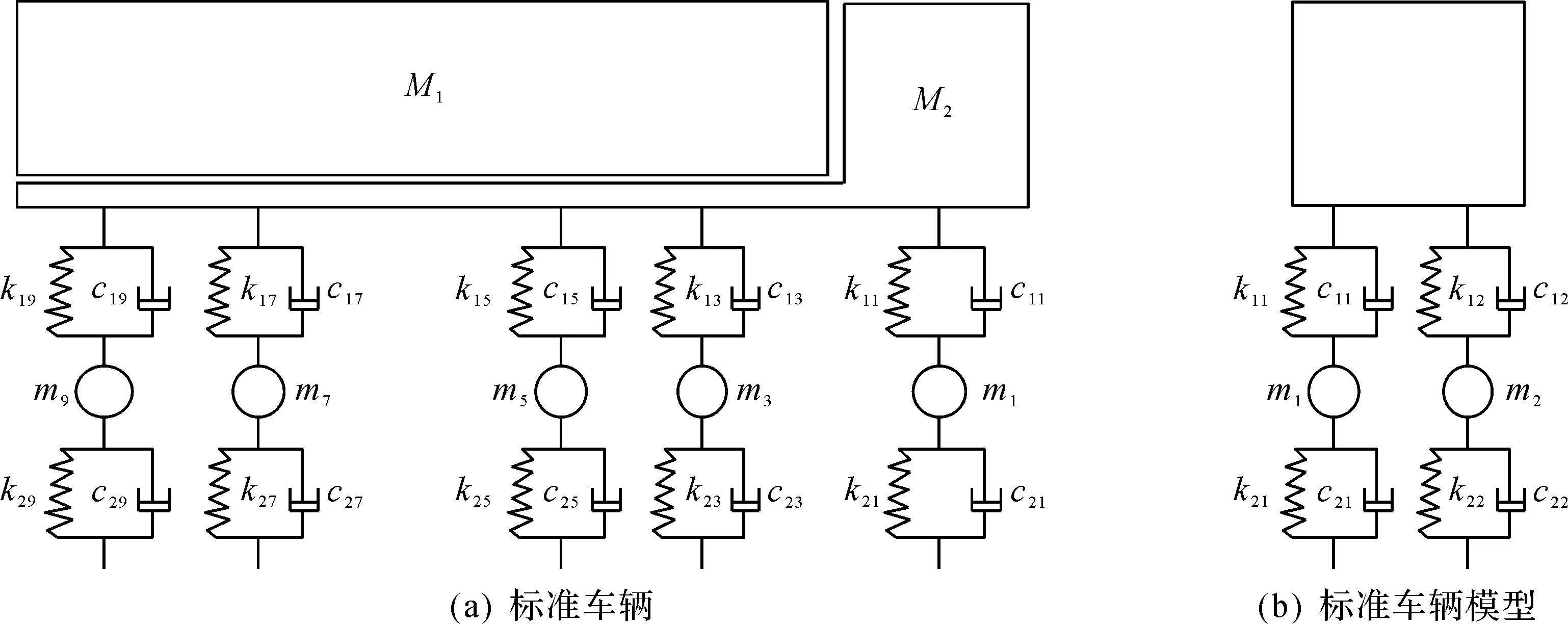
图3 整车车辆模型示意图

表1 车辆模型参数

2.2 全桥模型

混凝土主梁按照设计图纸采用CAITIA V5建立精细化模型，主梁模型如图4所示，并导入ABAQUS生成实体部件，该模型分别考虑了混凝土箱梁截面变化、箱式腹板和顶底板的厚度变化；钢箱梁模型采用壳单元进行建模。因钢混结合段处混凝土箱梁为实心截面，刚度较大，故整体模型建立时简化了钢混结合段的钢箱梁细部结构设置，只将钢箱梁两端2.25 m范围单元嵌入混凝土箱梁实心端部区域。

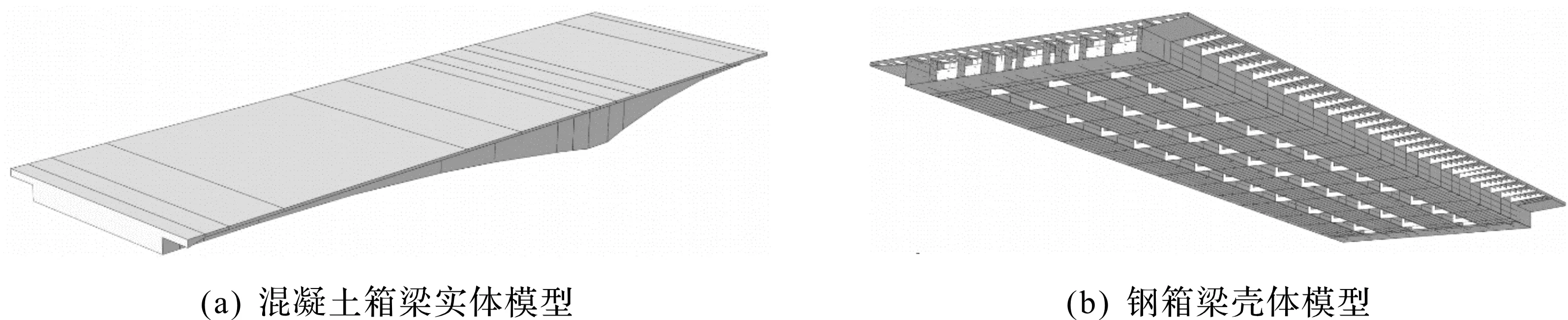
图4 主梁模型

2.3 移动荷载工况设置

笔者主要对移动车辆作用下桥梁的动力响应进行数值分析，其中车辆行驶速度、车辆轴重等均是影响桥梁动力的主要因素，故设置两种工况进行研究。

工况1单辆55 t荷载车辆沿中车道行驶，速度分别为5，10，15，20，25，30，35 m/s。

工况2单辆车辆以25 m/s速度沿中车道行驶，车辆载重分别为15，25，35，45，55，70，90，110，120 t。

3 冲击系数计算分析

3.1 规范冲击系数计算方法

冲击系数是评估桥梁承受车辆作用的指标，根据《公路桥涵设计通用规范》[13]，冲击系数m的计算式为

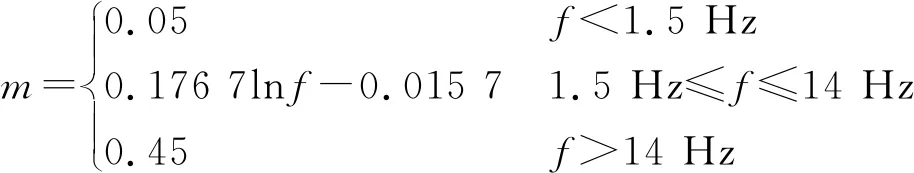
(1)

式中f为结构基频。

根据车辆在桥梁实际行驶时的情况，冲击系数公式为

(2)

式中：μ为冲击系数；RD为桥梁在车辆作用下的最大动态响应；RS为桥梁在车辆作用下的最大静态响应。

式(2)可以选择位移、弯矩和应变作为其响应进行计算，笔者采用竖向位移作为其动力响应因素计算冲击系数。

运用ABAQUS的Lanczos特征值求解器对金溪大桥全桥振型和自振频率进行计算，得到全桥前100 阶自振频率，其中前20 阶自振频率如表2所示。

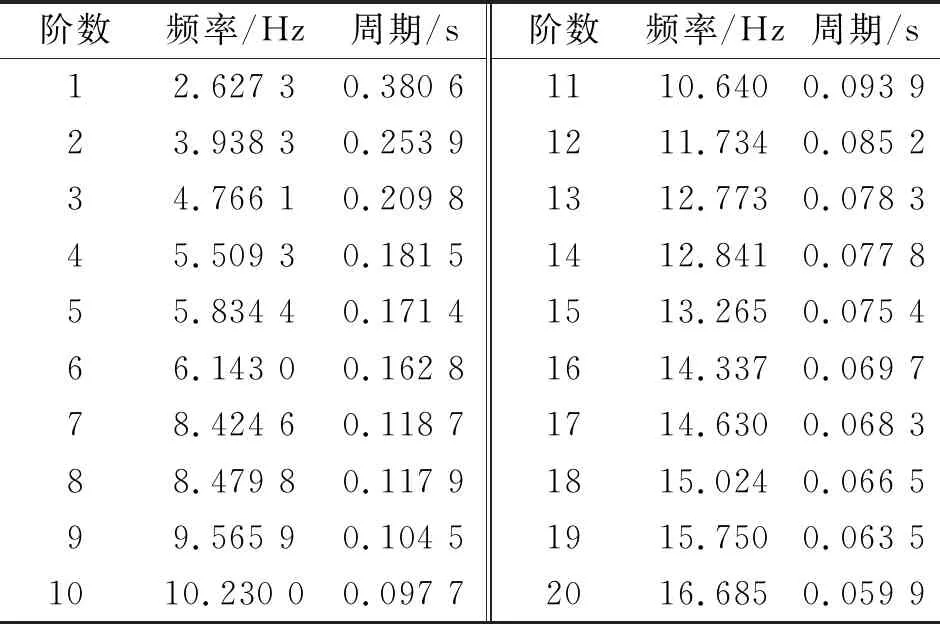
表2 前20 阶自振频率和周期

由表2可知：该桥梁第一阶振型自振频率为2.627 3 Hz，根据上文所述中国公路桥梁通用设计规范的冲击系数计算方法可求得冲击系数，约0.155左右。

笔者以位于金溪大桥边跨跨中位置1-1截面、中跨跨中位置2-2截面两个控制截面为研究对象，对混合梁桥动力响应进行研究，主梁动力响应控制点位置如图5所示。边跨跨中截面主要以混凝土箱底板中部A点为对象，对其竖向位移进行分析；中跨跨中为钢箱梁截面，为便于研究钢箱梁各分离箱动力响应，分别对边钢箱B点及中钢箱C点竖向位移进行分析。

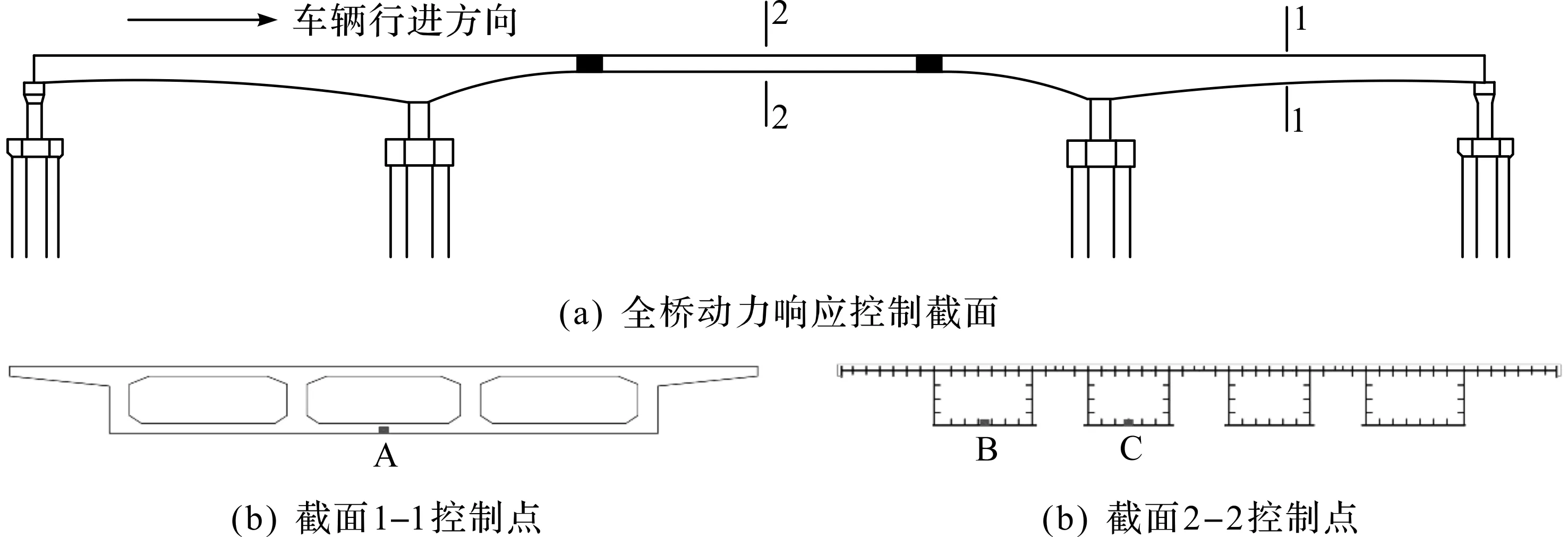
图5 主梁动力响应控制点

3.2 车速对冲击系数的影响

以各点竖向位移计算得到随车辆行驶速度变化的位移冲击系数曲线，如图6所示。由图6可知：各点冲击系数并不是随速度增加而单调递增，随着车辆行驶速度的增加，边跨混凝土箱梁及中跨边钢箱及中钢箱位移冲击系数呈现波动上升的趋势；其中边跨混凝土箱梁的位移冲击系数在速度为25 m/s时出现下降，在30 m/s时出现大幅增长并达到最大值，而中跨边钢箱和中钢箱的位移冲击系数变化及数值都较为一致，在车辆行驶速度较小时逐渐增大，在车辆行驶速度达到25 m/s后基本达到稳定，但均小于规范计算所得容许冲击系数。

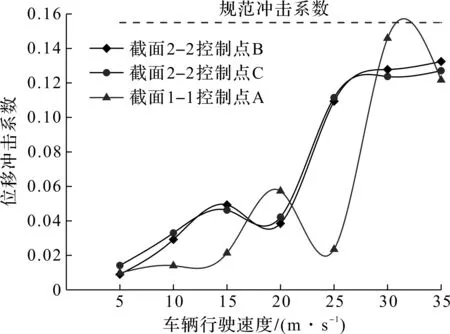
图6 不同速度行驶位移冲击系数

3.3 车辆轴重对冲击系数的影响

以各点随加载车辆轴重变化的位移冲击系数曲线如图7所示。由图7可知：各点位移冲击系数并不是单纯随着车辆轴重的增加而单调减小，对于A点所在的混凝土箱梁，当加载车辆轴重为30～70 t时，冲击系数逐渐减小，但当车辆荷载增加到90 t时，冲击系数出现小幅增大，随后继续减小，冲击系数整体保持在0.04左右。对于B点和C点所在的边钢箱与中钢箱，其冲击系数大小及变化趋势基本一致，当车辆轴重为45 t时位移冲击系数达到最大，约为0.12，在车辆轴重变化过程中，冲击系数基本稳定在0.1，同时混凝土及钢箱梁冲击系数也都小于规范计算值。

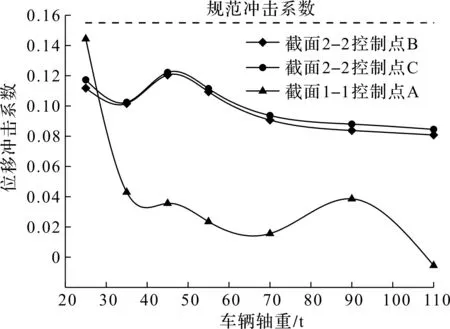
图7 不同轴重行驶位移冲击系数

4 结 论

对于分离式钢箱梁混合梁桥，通过分析其位移冲击系数变化可以得出：1) 其混凝土边跨和钢箱梁中跨的位移冲击系数随着车辆行驶速度增加，边跨混凝土箱梁冲击系数在车速为25 m/s时出现减小，并随后出现大幅增长；中跨钢箱梁冲击系数在车速为20 m/s时出现小幅减小，而后在25 m/s时出现较大增长，并逐渐趋于稳定。2) 随着加载车辆轴重增加，边跨混凝土箱梁的冲击系数逐渐减小，但在加载车辆达到90 t时冲击系数有一定的增加；中跨分离式钢箱的边钢箱和中钢箱冲击系数变化规律基本一致，其冲击系数随着轴重的增加，在达到45 t时达到峰值，随后逐步减小并逐步趋于稳定。3) 分离式钢箱的边钢箱及中钢箱在两种不同工况情况的位移冲击系数变化趋势及数值基本保持一致，说明分离式钢箱其整体性能能够保持一致，能够实现受力上的整体协调。同时包括边跨混凝土箱梁的位移冲击系数在内，三者的位移冲击系数基本都小于规范计算冲击系数，足以满足混合梁桥的实际使用要求。