加筋板的累积损伤力学模型研究
吴剑国,王锦琦,叶 帆,傅何琪,申屠晨楠
(1.浙江工业大学 土木工程学院,浙江 杭州 310023;2.中国船舶及海洋工程设计研究院,上海 200011)
随着船舶结构的大型化,结构疲劳事故频出,船舶结构低周疲劳问题引起了业界的广泛关注。Urm等[1]于2004年对油船的低周疲劳问题进行了研究,考虑多个因素对结构的损伤累积影响,初步给出了计算船体梁低周疲劳的方法。田雨[2]基于损伤力学和塑性力学,分析了低周疲劳损伤并建立了船体梁剩余强度的评估方法。Ming等[3]基于有限元软件,分析了非线性有限元模型对循环荷载下船体梁极限弯矩的影响;Yang等[4]基于Smith的船体梁极限强度计算方法,提出了一种循环荷载下船体梁极限强度的简化计算方法;汪丹等[5]针对船体梁基本的加筋板构件,提出了循环荷载作用下加筋板结构的累积递增塑性应变模型。余明辉等[6]基于两端固支的梁-柱模型,建立了循环载荷作用下加筋板单元力学模型。孟志光等[7]通过引入一种等效材料本构模型,提出了能考虑结构层面损伤累积的加筋板单元力学模型。由此可见:现有工作没有考虑材料层面的损伤,循环荷载下加筋板的滞回曲线与实际的尚有较大偏差,计算精度还不够高,还需要深入研究。
笔者改进材料损伤变量模型,再将其引入加筋板的极限强度集中之中,提出一种能够考虑材料累积损伤的加筋板单元力学模型。采用VB语言编制加筋板在循环载荷作用下的的滞回曲线的计算程序,给出一个加筋板的算例,并采用非线性有限元方法进行精度验证。
1 循环载荷作用下的钢材本构模型
加筋板在循环载荷的作用下,不仅可能会发生屈服,更可能发生屈曲。一旦发生了屈曲,将产生较大的损伤,即使卸载后拉伸也不可能恢复屈曲前性能,这一特点导致加筋板在往复载荷作用下,较一般只考虑屈服强度,不发生屈曲破坏的结构损伤更大。根据这一特点提出了适用于加筋板屈曲的材料损伤变量定义,并将其引入到材料本构模型[8]中,提出了循环载荷作用下的加筋板的材料本构模型,即平均应力—应变关系。
如图1所示,按照平均应力—应变关系,可得到钢材的加载图。先压后拉加载,从O点开始压缩加载,沿着钢材压缩骨架曲线,经过OA弹性段、AB强化段、进入BH损伤段,到达卸载点C点时,弹性卸载至D点。再进行拉伸加载,沿着再加载曲线到达E点,E点在拉伸骨架曲线上取,接着弹性卸载至F点。第2圈时,需考虑上一圈加载所产生的的损伤,根据退化准则峰值点由C点折减至G点,刚度E也发生折减。此时压缩则沿着再加载曲线到G点,再进入新损伤段GH,到达第2次卸载点I,按折减后的弹性模量卸载至J点,之后的加载同第1圈。
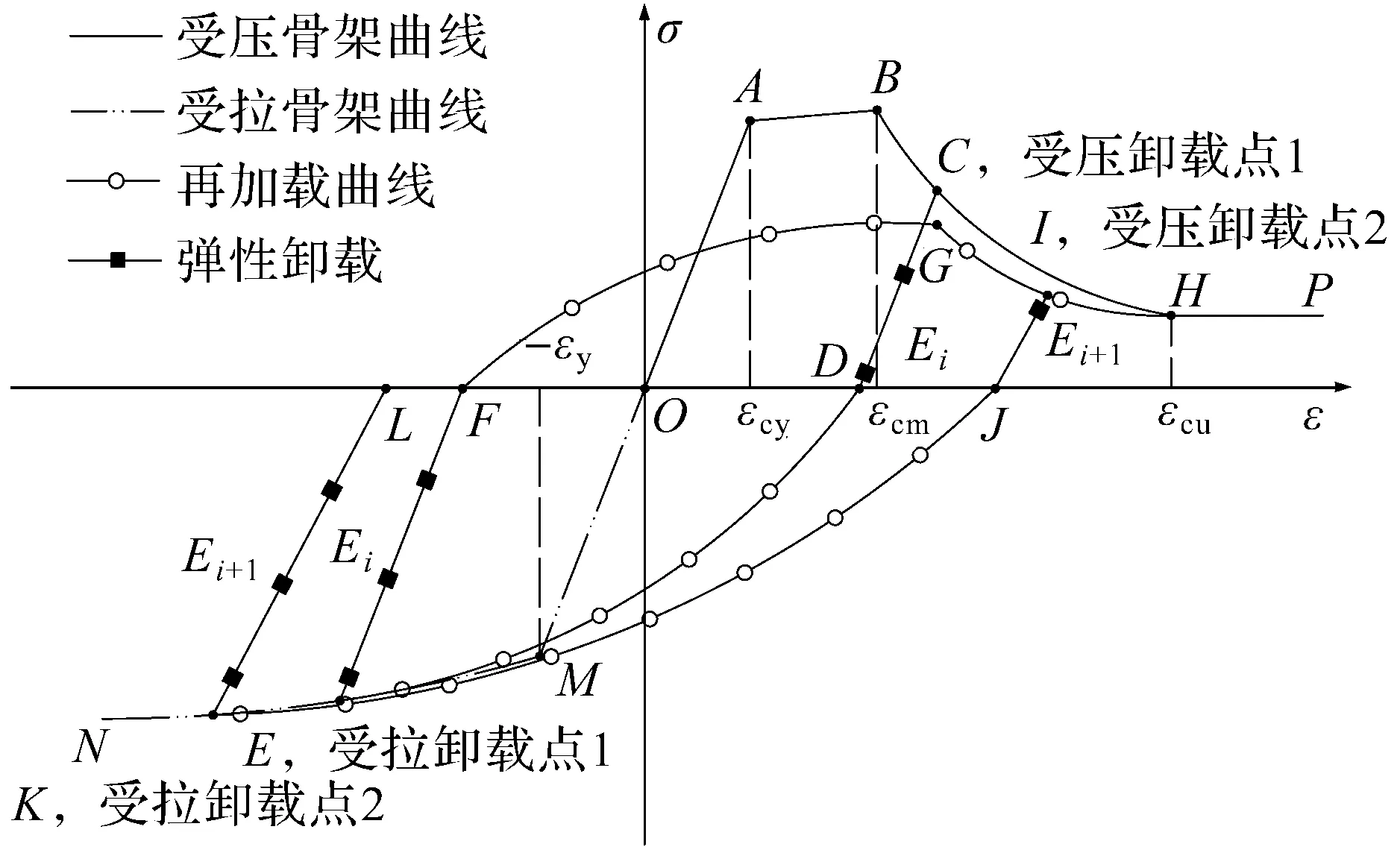
图1 循环荷载下钢材应力—应变关系
1.1 材料骨架曲线
材料骨架曲线分为压缩和拉伸骨架曲线,对各种钢材都适用。
1.1.1 压缩骨架曲线
压缩循环骨架曲线分为OA,AB,BH,HP共4 段,具体的表达式为
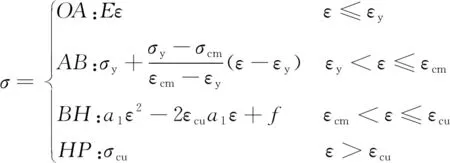
(1)
式中:σ为应力;ε为应变;E为弹性模量;σy为屈服应力;σcm为损伤临界应力;σcu为剩余强度;εy为屈服应变;εcm为损伤临界应变;εcu为退化终点应变;a1和f为二次函数相关系数,取值与材料强度相关。
1.1.2 拉伸骨架曲线
拉伸循环骨架曲线分为OM和MN2段,具体表达式为
(2)
1.2 再加载曲线
再加载曲线为卸载曲线起始点到终点的曲线,具体表达式为
σ=E(ε-ε0)+σ0-η(E-Ek)(ε-ε0)
(3)
式中:σ,ε含义同式(1);ε0,σ0分别为曲线起始点的应变和应力;εP,σP分别为峰值点的应变和应力;η为曲线调调整系数;Ek为割线刚度。
1.3 退化准则
1.3.1 损 伤 量
钢材在反复荷载作用下的材料损伤的程度用损伤变量表示,其具有如下性质:1)损伤变量D应在[0,1]取值,当D=0时,表示材料没有损伤;当D=1时,表示材料已经完全破坏。2)损伤变量D是一个单调递增函数,即随着损伤发展不断增大,不会下降。造成损伤的因素有很多,其中众多学者从能量、变形、变形和能量的综合3 个方面着手,提出了多种损伤变量模型,比如:Darwin等[9]和Ibarra等[10]的能量损伤模型,沈祖炎等[11]的变形损伤模型,欧进萍等[12]的变形和能量模型。
通过计算初步分析了以上4 种损伤模型,发现同时考虑变形和能量的欧进萍等[12]模型对于损伤的预测最为准确,但需不断积分计算滞回耗散能量,计算效率低;Darwin等[9]模型和Ibarra等[10]模型趋预测趋势也比较准确,也需要不断地积分计算滞回能;其中沈祖炎等[11]的模型虽只考虑变形的影响,结构形式简单,但损伤预测结果准确,且容易在损伤计算程序中实现。因此根据沈祖炎模型,为考虑实现加筋板的屈曲损伤,提出了可以计算加筋板累积损伤的模型,其合理性可能还需进一步的验证,具体公式为
(4)
式中:εi,max为钢材发生的最大塑性应变;εy为钢材屈服应变;εi为钢材在第i圈发生的塑性应变;εu取为加筋板单调加载极限屈曲应变εend;λ=0.008 1;N为循环荷载的半循周数。
1.3.2 退化公式
根据沈祖炎等[11]的材料损伤退化公式,并结合上述材料骨架曲线和材料的退化准则,分强度退化和刚度的退化,退化公式具体为
σi+1,max=(1-ζ1Di)σi,max
(5)
Ei+1=(1-ζ2Di)E
(6)
式中:σi,max,σi+1,max分别为第i次和i+1次的峰值应力;Ei+1为第i+1次弹性模量;E为弹性模量;系数ζ1=0.42,ζ2=0.12;Di为第i次的损伤量,按式(4)计算。
2 循环荷载下的加筋板单元力学模型

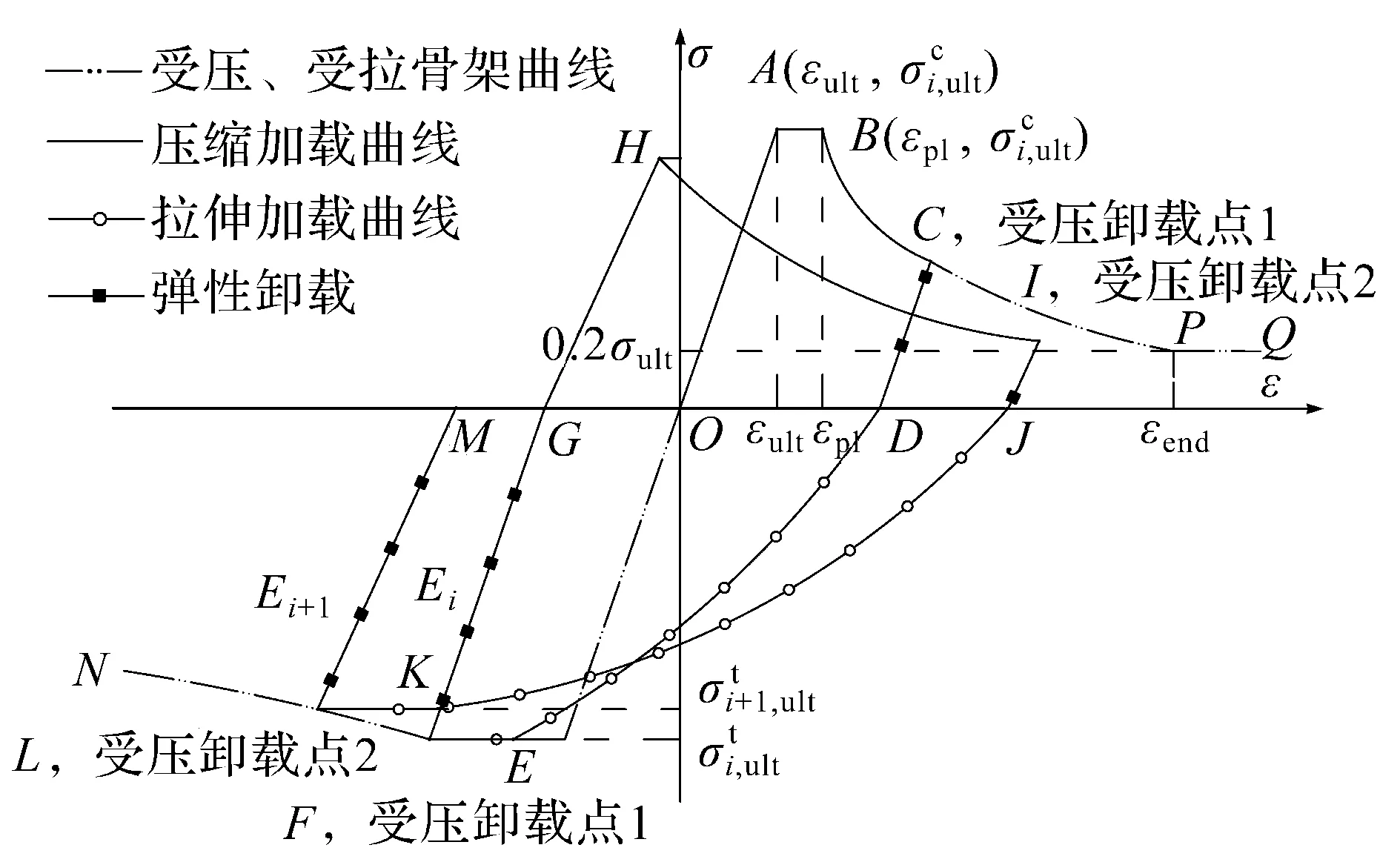
图2 循环荷载下加筋板应力—应变关系
2.1 极限强度
加筋板极限强度是计算应力应变的基础,求得了极限强度才可以进行应力应变计算。从图像上看,其决定了AB非卸载区、EF平台段这上下边界的取值,如图2所示。
2.1.1 压缩极限强度
根据加筋板单元压缩失效特点,只考虑其中两种受压失效模式,采用Hughs[14]推导的加筋板极限强度公式计算。
1) 面板受压失效模式为
(7)
式中:σF为上述钢材损伤折减后的屈服强度;σuf为待求的面板受压的极限强度;M0,δ0分别为侧向荷载作用时跨中的弯矩和挠度;yf为面板厚度中心与截面形心轴之间的距离;I,A分别为横截面的惯性矩和面积;γ,ν均为挠度系数;Δ为初始偏心;Φ为轴力放大因子。
2) 带板受压失效模式为
(8)
(9)
式中:σF同式(7);σue为待求的带板受压的极限强度;yp为带板厚度中心与截面形心轴之间的距离;Ie,Ae分别为横截面的有效惯性矩和有效面积;Δp为板的刚度下降引起的偏心距;M0,δ0,γ,ν,Φ,A含义同式(7)。
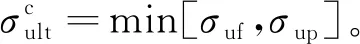
2.1.2 拉伸极限强度
将上述计算的钢材屈服强度取负号作为拉伸极限强度,其计算式为
(10)
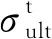
2.2 平均应力—应变关系
2.2.1 受压方向平均应力—应变关系
加筋板格单元受压的平均应力—应变关系,采用Rahman等[13]提出的公式,其平均应力—应变关系曲线有4 段:OA段、AB段、BP段和PQ段,也如图2所示,公式如下:
1)OA段(0<ε≤εult)计算式为
(11)

2)AB段(εult<ε≤εpl)计算式为
(12)
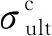
3)BP段(εpl<ε≤εend)计算式为
(13)
(14)
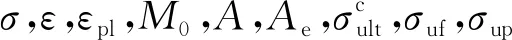
4)PQ段(εend<ε)计算式为
(15)

2.2.2 受压单元的卸载
规定压缩卸载CD段遵循2 个原则:1) 在任何阶段开始卸载都为弹性卸载;2) 卸载刚度用上述钢材折减后的弹性模量。
2.2.3 受拉方向平均应力—应变关系
加筋板的反向加载会出现刚度软化现象。前半段为指向峰值点的一条曲线,后半段为平台直线,分为DE和EF共2 段,公式如下:
1)DE段计算式为
(16)
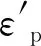
2)EF段计算式为
(17)
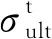
2.2.4 受拉单元的卸载
拉伸卸载FG段同2.2.2节。每一圈加载均按照压缩加载、压缩卸载、拉伸加载、拉伸卸载等4 个顺序进行加载,且各圈的计算公式均一致。
3 编程与有限元计算
采用Visual Basic 6.0语言对所提方法编程,并采用Abaqus软件进行对比计算。程序主要分为材料和加筋板2 个计算循环,计算流程如图3所示。

图3 计算流程图
3.1 加筋板模型参数
选取一个加筋板单元进行计算,其尺寸如表1所示。其中钢材屈服强度σs=235 MPa,弹性模量E=2.06×105MPa,泊松比ν=0.3。有限元模型用板单元进行建模,钢材使用弹塑性本构关系,如图4所示。

表1 加筋板单元尺寸
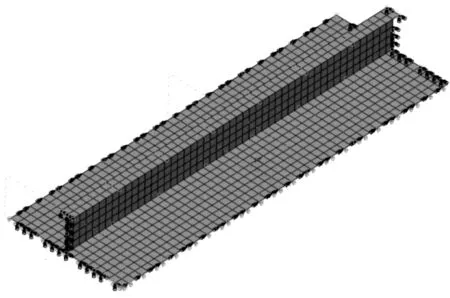
图4 ABAQUS有限元模型示意图
3.2 计算结果比较
3.2.1 等幅循环加载
采用加载制度:0~2.5εy的加载应变,双向等幅加载4 次,先压缩后拉伸。计算结果的极限强度比值和损伤量汇总如表2所示。计算结果的加筋板格单元和材料平均应力—应变曲线如图5所示。

表2 等幅荷载下加筋板极限强度比和损伤量
图5 等幅荷载下钢材和加筋板滞回曲线
3.2.2 递增循环加载
采用加载制度:0~1.0εy,0~2.0εy,0~3.0εy,0~4.0εy的加载应变,双向等幅加载,每级加载1 次,先压缩后拉伸。计算结果的极限强度比值和损伤量汇总如表3所示。计算结果的加筋板格单元和材料平均应力—应变曲线如图6所示。

表3 递增荷载下加筋板极限强度比和损伤量
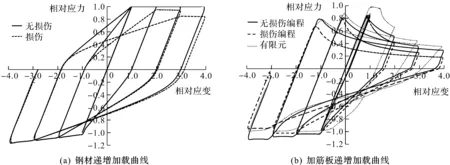
图6 递增荷载下钢材和加筋板滞回曲线
综上可知:1) 钢材滞回曲线中,不考虑损伤的受压和受拉屈服点基本不会下降,考虑损伤的屈服点在逐步下降;2) 加筋板滞回曲线中,笔者方法和有限元计算出的极限强度均在逐步下降,不计损伤的方法几乎没有下降且拉伸极限强度在逐步增强;3) 等幅和递增两种循环荷载的理论计算结果与有限元结果吻合较好;4) 等幅荷载下的前几级损伤显著高于递增荷载下的材料损伤,但递增荷载下材料损伤量后续增加较快,这是因为递增荷载前几级加载应变较小则其损伤也小;5) 有限元的压缩峰值点会略高于笔者结果,因其考虑了一定的钢材强化;6) 加载应变需达到一定的门槛,才会产生损伤。
4 结 论
分析计算了钢材损伤,在等效材料本构模型基础上提出考虑损伤的加筋板格单元力学模型,使用Visual Basic 6.0编程计算。结果表明:引入材料损伤之后,加筋板单元的屈服强度和刚度随着损伤量变大都在不断地下降,且与未引用材料损伤力学模型结果相比,具有更好的精度。后续,笔者还将开展加筋板单元在循环载荷作用下的结构承载力试验,进一步验证所提模型的精度。

