一种星球探测六足轮腿机器人的设计与运动规划
秦日鹏,徐坤,陈佳伟,韩亮亮,丁希仑,*
1. 北京航空航天大学 机械工程及自动化学院,北京 100083 2. 上海宇航系统工程研究所,上海 210019
六足机器人由于具有很强的地貌适应性,非常适合在凹凸交错复杂的岩石表面或土质松软的表面环境运动,一直是星球探测机器人[1-2]研究的重要方向。从19世纪开始,美国麻省理工学院相继开发出Genghis[3]、Hannibal[4]和Attila[5]等六足机器人用于执行复杂的星球探测任务。该系列机器人按照分层、模块化的思想制造,每条腿都作为单独的模块进行控制。美国国家航空航天局(NASA)实验室提出了月球表面的模块化六足概念机器人Habitat[6],其单腿结构为双杆并联机构,可以拼接起来形成模块化的月球基地。2005年,美国喷气动力实验室成功研制出一种用于太空环境下小尺寸安装、维修探测等作业的空间六足机器人Lemur[7-8]。该机器人的腿融合了多种不同功能,其中两条腿除行走功能外还具备操作能力。卡内基-梅隆大学研制的六足火星漫游车Ambler[9]的每条腿分支包含一个转动副和一个移动副,该两运动副轴线平行能够保证机器人本体始终保持水平状态。
相对于腿式机器人,轮式机器人具有在平坦地面上移动速度快、稳定性好的优点。目前成功登陆外星的星球探测机器人都是以轮式结构为主的机器人,包括苏联的“月球车1号”和“月球车2号”,中国的“玉兔一号”和“玉兔二号”[10],美国的“勇气号”“机遇号”“好奇号”等。为了充分利用轮式和腿式机器人的特点,将六足轮腿机器人用于星球探测。NASA研制了一种用于星球探测的六轮腿式机器人ATHLETE[11-12],该机器人每条腿末端均安装了主动轮,可以实现轮腿两种运动,还可以进行土壤采样工作。北京航空航天大学和意大利米兰理工大学合作研制的NOROS系列星球探测机器人[13]主动轮安装在小腿上,通过构型切换实现轮腿两种运动模式。该机器人外壳采用半球形,可以实现倾倒恢复等功能。中国空间技术研究院设计了一种六轮腿式可移动载人月面着陆器[14],对该着陆器着陆过程进行了任务分层,并进行了一种软着陆的运动规划。
相对于轮腿式的星球探测机器人,球形星球探测机器人[15-17]可以将着陆、缓冲减振和移动功能统一,不受着陆区域地形的限制,极大地拓展了应用范围。受球形机器人对称结构的启发,基于现有的具有中心对称结构的六足机器人[18]设计了一种具有高度对称性的六足轮腿机器人。该机器人的结构不仅在机身水平面内中心对称,而且关于机身水平面对称,同时单腿运动范围关于机身水平面对称。机器人的主动轮与膝关节同轴,使机器人在轮行模式下可以调节机身高度。在星球着陆、倾倒恢复、空间站舱壁移动等特殊应用情况下,可避免由机器人的方向性带来的问题,使机器人在星球探测中具有更好的适应性。设计了一种适合在无视觉传感和局部地图的条件下[19]仅依靠足底力传感器和机身惯性测量单元,实现稳定连续行走的自适应步态。基于指数坐标在SE(3)空间上对机器人机身运动进行规划,避免了利用传统欧拉角规划在特殊姿态的奇异性,同时统一了位置和姿态的规划。利用该机器人关于机身水平面对称的特点,提出了一种倾倒恢复运动策略。
1 机器人设计与运动分析
1.1 机器人设计
六足轮腿机器人的整体结构如图1所示。该机器人由1个机身和6条相同的轮腿分支组成。机身的外壳形状为关于机身水平面对称的椭球面;6条轮腿分支在机身水平面内关于机身几何中心对称分布,每条分支具有3个转动自由度(腰关节、髋关节和膝关节)和1个主动轮的转动自由度,且每条分支的工作空间关于机身水平面对称。
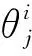

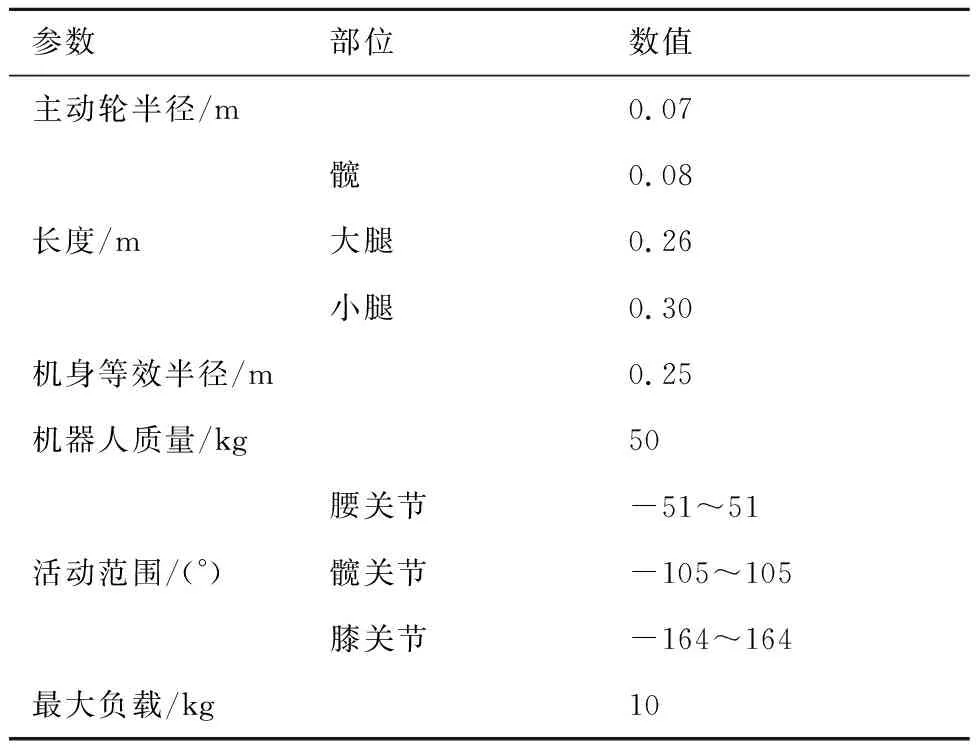
表1 六足轮腿机器人的参数Table 1 Parameters of wheel-legged hexapod robot
轮腿分支具体结构如图2(a)所示,髋关节和膝关节的驱动电机嵌入大腿内部,增加了机器人、腰关节的运动范围,小腿采用简单的碳纤维空心圆管,降低了腿分支的转动惯量。膝关节的驱动电机布置在靠近髋关节的位置,通过双平行四边形机构传动解决现有足式机器人膝关节平行四边形传动机构在主动曲柄与连杆共线时会产生奇异位形,从而产生两种可能的运动限制膝关节的运动角度的问题。在平行四边形机构的连杆与机架之间加入一根辅助杆件(连架杆)形成双平行四边形机构,解决运动奇异性问题(保证运动的唯一性),示意如图2(b)所示。
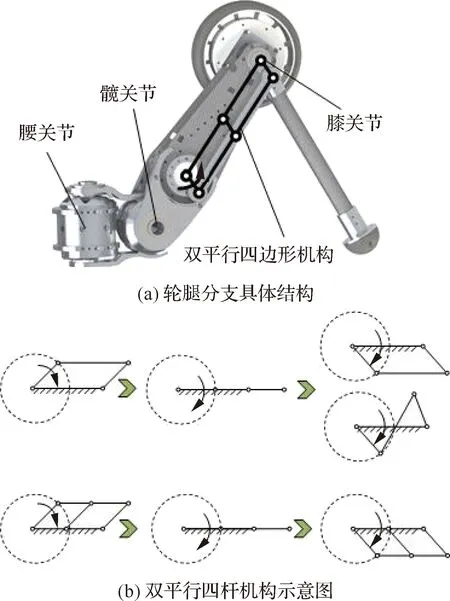
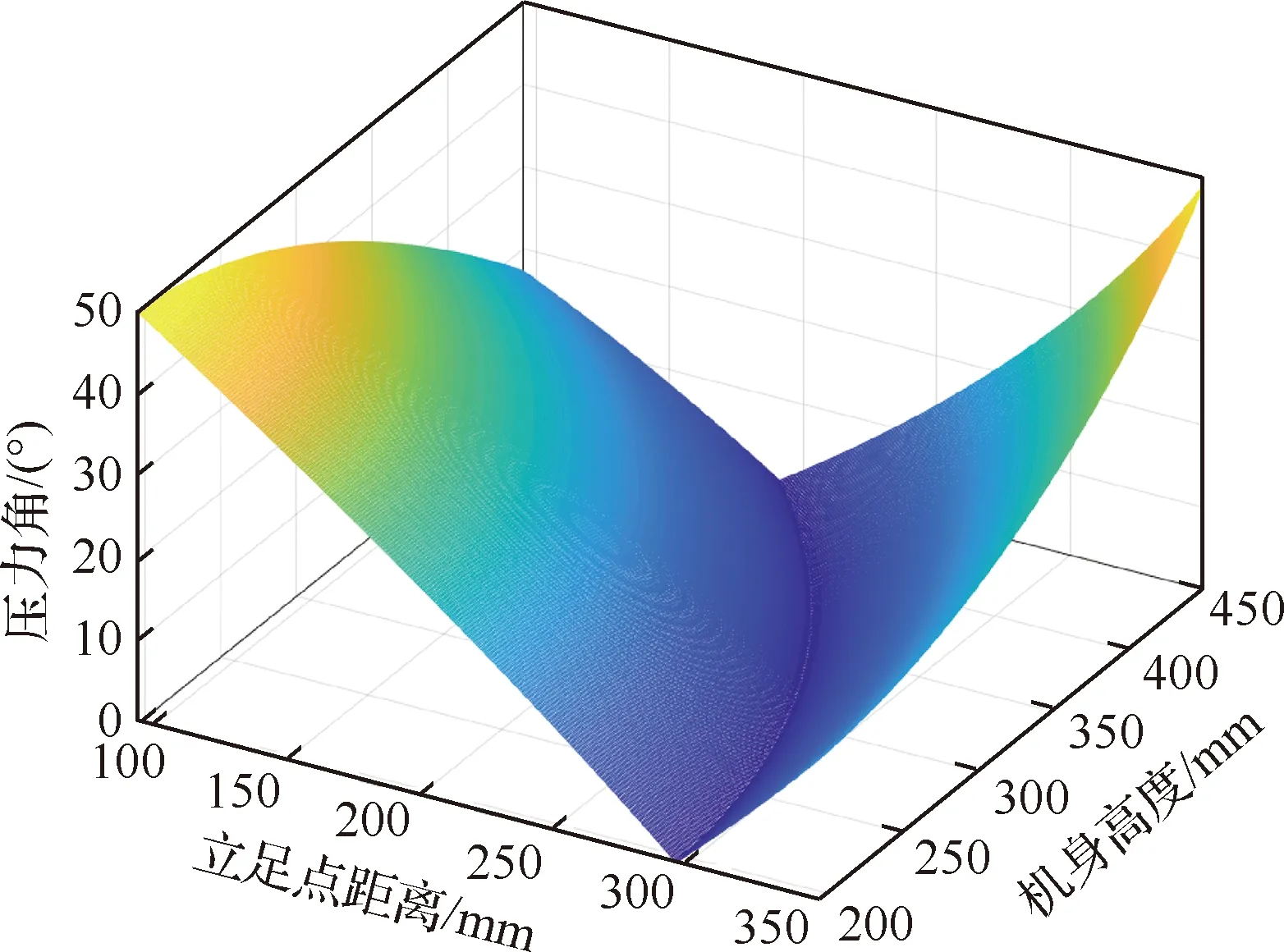
在奇异位置时辅助杆件使机构的运动学有唯一解,在非奇异位置时双平行四边形机构的运动与平行四边形机构的运动完全等效。当膝关节角度为0°(小腿伸直)时,双平行四边形机构到达奇异位置。机器人在运动模式切换及倾倒恢复的过程中,为了切换构型双平行四边形机构会经过奇异位置,此时负载仅为小腿。双平行四边形机构的压力角由机器人机身高度和机器人立足点共同决定,图3所示为双平行四边形机构压力角与立足点和机身高度的关系。该机器人实际行走、作业时受到关节电机功率限制,在所能达到的有效工作空间内(机身高度在195~450 mm之间,机器人立足点到腰关节轴线的距离在95~350 mm之间),双平行四边形机构的压力角小于50°,满足机构设计的要求。
1.2 轮行运动学分析
机器人的轮行模式如图4所示。在轮行模式中,机器人可选择3~6条分支支撑机身进行运动。支撑机身的分支数量越多,机身稳定性越好,但转弯性能越差。

图4 轮行模式Fig.4 Wheeled mode
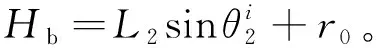
(1)
式中:dωi为第i条分支上主动轮控制机身高度的角速度的大小,具体方向由实际结构决定。
1.3 足行运动学分析
由于结构和运动的对称性以及较大的关节运动范围,机器人可以实现多种构型的足行模式更好地适应不同的地形。该机器人足行模式如图5所示。
单个腿分支的结构可以看作是一个三自由度串联机构。单腿足末端的位置可以使用串联机构的指数积公式进行求解,具体可以表示为
(2)

(3)


图5 足行模式Fig.5 Legged mode
1.4 运动模式切换运动规划
机器人可以通过构型变化实现轮行模式和足行模式运动切换,如图6所示。机器人从轮行模式切换至足行模式可以分为以下3个步骤:

图6 轮行和足行模式切换Fig.6 Planning between wheeled and legged modes
1) 机器人3条轮行状态的分支调整机身到合适的高度,与此同时,另外3条分支从轮行构型切换至足行构型(足端高度高于地面)。
2) 机器人3条足行状态的分支末端向下运动直到接触地面开始支撑机身;然后机器人足行分支提升机身高度到期望值,同时3条轮行状态的分支切换至足行构型(足端高于地面)。
3) 机器人3条摆动状态的分支的末端竖直向下运动,直到接触地面开始支撑机身。机器人进入足行模式。
机器人从足行模式转换成轮行模式,可以看作是从轮行模式切换至足行模式的逆过程。
2 自适应步态设计
为了应对星球探测中局部无光照和无地图的特殊境况,同时提高机器人在星球探测过程中的适应性,设计了一种仅依靠机身惯性测量单元和足底力传感器的自适应步态。典型的三角步态具有较高的稳定性,同时具有较高的行进速度,以三角步态作为基础设计自适应步态。以典型的三角步态为设计基础在一定程度上限制了机器人在极端地形上的运动能力,但简化了在复杂地形上的运动规划。
该自适应步态的整体运动规划如图7所示。机器人的步态参数主要包括机身的理想高度H0、期望的移动速度v0和最大步长Lmax。步态参数可以根据境况实时修改,并在下一个六足支撑状态开始生效。六足支撑状态是切换所有分支摆动相和支撑相的一个关键的过渡状态。在六足支撑阶段,每条分支的状态根据之前的状态进行交替变化。若下一组支撑分支中存在没有接触地面的情况,则机器人在进入下一个阶段会倾倒(恢复的方法详见第3节)。为了适应未知的地形环境,保证机器人机身的连续稳定运动,设计了虚拟支撑平面作为运动参照。状态分析模块将6条分支分为支撑相和摆动相进行不同的运动规划。处于支撑相的分支在规划完机身运动后,利用逆运动学求解关节期望速度;处于摆动相的分支直接利用摆动分支的运动规划求解关节期望速度。当摆动相的3条分支全部触地进入支撑相后,机器人进入六足支撑状态。

图7 自适应步态运动规划框图Fig.7 Diagram of adaptive gait motion planning
2.1 虚拟支撑平面
在无全局地图的条件下,仅可知道机身的姿态和立足点相对于机身的位置。为了保证机器人运动的连续性和稳定性,建立一个虚拟支撑平面用于机器人的运动规划。虚拟支撑平面如图8 所示。

图8 虚拟支撑平面Fig.8 Virtual supporting plane
假设星球的重力加速度为g,垂直于重力方向的平面定义为水平面,期望机身的前进速度为v0,机器人3条摆动分支最后的立足点为P1、P2和P3。虚拟支撑平面平行于水平面,并且高度为立足点高度的平均值。机器人3条摆动分支真实的立足点在虚拟平面的投影为点Q1、Q2和Q3。由于地形是复杂且不平整的,为了建立运动的参照更好地保证机器人运动的连续性,基于虚拟支撑平面建立一个固定的虚拟坐标系B。虚拟坐标系B的原点建立在3个立足点的投影(Q1,Q2,Q3)形成的支撑三角形的内心(到3条边的距离相等),x轴平行于期望运动方向,z轴平行于重力且方向相反。机器人可以基于新坐标系B刷新当前机器人机身的位置和6个立足点的位置,表示为
(4)
(5)

2.2 基于指数坐标在SE(3)空间的机身轨迹规划
在虚拟坐标系B下,为了避免利用欧拉角求解的奇异性,利用指数映射在SE(3)空间对机器人的机身位姿轨迹进行运动规划。假设在虚拟坐标系B下,机身的初始位姿表示为
ξ0=lgG0
(6)
式中:ξ0为机身位姿的指数坐标;lg为指数映射的反运算(对数运算)[20];G0为机身的位姿矩阵。在虚拟坐标系B下,机器人几何投影最稳定的点就是坐标系原点,所以机身最终期望位置的投影就是坐标原点。为了保证每条支撑腿工作空间相近,机身最终期望的姿态平行于真实立足点形成的支撑三角形。在当前虚拟坐标系B下,机身的最终期望位姿的指数坐标表示为
(7)

在指数坐标系下表示机器人的位姿不仅能避开奇异性,还能将位姿映射成六维欧氏空间,便于使用搜索算法规划机身轨迹。基于该机器人机构工作空间分析,用三次曲线进行插值规划,机身在指数坐标系下的运动可以表示为
ξ=ξ0+a2t2+a3t3
(8)

(9)

2.3 摆动分支运动轨迹规划
在虚拟坐标系B下,为了更好地利用摆动分支的工作空间适应地形,使用一种简单的轨迹搜索算法实现摆动分支的运动规划。每条摆动分支使用相同的运动规划方法,单腿的摆动轨迹如图9所示,可以将其分为3个阶段:
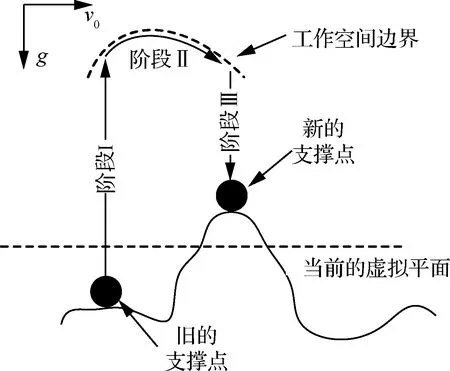
图9 摆动分支的运动规划Fig.9 Motion planning of swing branch
阶段Ⅰ摆动分支的末端从旧的支撑点出发,平行于重力方向向上移动,直到到达工作边界(实际应用中,给出一定的稳定边界距离)。
阶段Ⅱ该阶段的主要目的是为了摆动分支末端向前移动,需要考虑两个因素:工作空间和是否接触地面。
为了能够最大限度地利用摆动腿的工作空间并降低运动规划的复杂性,将摆动分支末端的运动空间网格化进行搜索,具体的搜索算法如图10所示。阶段Ⅱ停止并进入阶段Ⅲ的边界条件为分支末端水平移动的距离到达最大步长Lmax或碰撞到地面(分支末端存在接触力)。

图10 阶段Ⅱ的搜索算法Fig.10 Search method of section Ⅱ
阶段Ⅲ摆动分支末端从阶段Ⅱ最后的位置竖直向下寻找新的支撑点。摆动分支末端以一个恒定向下的速度(大小为vfz0)进行搜索:当机器人摆动分支末端的力传感器检测到力时,开始判定是否接触到地面;当机器人到达工作空间边界时,该分支结束摆动阶段(机器人可能倾倒,恢复的方法详见第3节)。
机器人利用阻抗模型来判定分支末端是否接触到地面。当分支末端力传感器存在反馈力时,摆动分支末端的搜索速度为
(10)
式中:vfz为搜索速度;F为当前分支末端力的绝对值;Fs0为判定的力阈值,一般设为稳定站立地面的支撑力。当F≥Fs0时,此时分支末端的位置为新的支撑点,该分支结束摆动阶段。
在地形局部高度落差不超过三足支撑下机身最大工作空间范围时,机器人可以使用该自适应步态进行探索性行走。
3 倾倒恢复运动规划
由于星球表面的复杂未知环境,机器人很容易在着陆时颠倒或行走过程中遇到凹坑等特殊环境而发生倾倒。由于机器人的结构和运动都是关于机身水平面对称的,所以机器人倾倒后只需在当前的状态下直接站立,不需再翻滚回到原有的状态。

图11 倾倒恢复运动规划Fig.11 Planning of stumble recovery
倾倒恢复的运动规划如图11所示,示意图如图12所示。倾倒恢复的运动规划可以分为以下3个阶段:
阶段1该阶段是为重新恢复机器人的足行状态做准备。在机器人发生倾倒且静止后,机器人分支进行运动进入构型S1。构型S1为一个中间过渡构型,所有分支的大腿在机身水平面内中心对称并且关于机身水平面对称,所有分支的小腿竖直向上。机器人等待机身静止后,切换到构型S2。构型S2是在构型S1的基础上,将3条间隔的分支切换到足行状态。机器人转换到S2构型后,进入阶段2。

图12 倾倒恢复示意图Fig.12 Diagram of recovery after stumble
阶段2该阶段主要利用3个足行状态分支寻找立足点。机器人在构型S2基础上,3条足行状态的分支竖直向下搜索立足点,方法与摆动分支轨迹规划的阶段Ⅲ相同。当3条足行状态的分支都找到支撑点后,建立虚拟支撑平面并且基于指数坐标在SE(3)空间上规划机身的运动,使机器人达到静态稳定(具体方法和自适应步态的机身轨迹规划相同)。机器人稳定机身后进入阶段3。
阶段3该阶段使机器人进入自适应步态的六足支撑状态。机器人将还未支撑的3条分支切换到足行状态,竖直向下搜索立足点。当3条摆动分支均搜索到支撑点后,机器人进入六足支撑状态。结束阶段3,机器人恢复到了正常的足行状态。
结合自适应步态和倾倒恢复的运动规划,机器人可以在复杂的环境中实现足行、倾倒恢复、继续足行的连续移动。相对于传统的自适应步态而言,这种运动规划方法在复杂和未知的星球探测中具有更好的适应性。
4 仿真验证
在Adams和MATLAB的联合仿真环境下,建立了该机器人的仿真模型,对该机器人的运动模式切换、自适应步态和倾倒恢复的运动规划进行仿真验证。惯性测量单元可以测量机身的姿态和重力方向,每个分支末端安装的一维力传感器可以测量足地之间的接触力,机器人和地面之间的接触使用经典的碰撞模型。
4.1 运动模式切换
该仿真过程分为机器人足行站立,足行模式切换为轮行模式,轮行模式移动,轮行模式切换为足行模式。
轮行运动主要针对机器人机身的高度调整的可行性进行仿真。在轮行运动的仿真中,使用三轮支撑机身,前进速度为0.8 m/s。机身高度设计的浮动值为0.07 m。机器人机身的初始高度为轮行模式的最高高度0.33 m。机身的高度使用正弦曲线进行规划,实际仿真结果如图13所示。

图13 轮行模式仿真结果Fig.13 Simulation result of wheeled mode
在轮行模式的仿真中,机器人机身在最高点是一个奇异位置。为了机身能够从最高点向下运动,髋关节和主动轮需要具有一定的初速度,使得机器人脱离最高位置。实验结果验证了在轮行模式中,机器人可以利用髋关节和主动轮的协调运动调节机身高度。
机器人的运动模式切换仿真分为两个部分,一个是从轮行模式切换到足行模式,另一个是从足行模式切换到轮行模式。机器人足行模式的初始腰关节、髋关节和膝关节的关节角度分别为0°、0°和90°。运动模式切换的仿真结果如图14所示。仿真的运动模式切换速度主要受机器人关节的最大运动速度影响(仿真用时5 s)。该仿真验证了轮行和足行两种模式相切换的运动规划的可行性。

图14 轮腿切换仿真结果Fig.14 Simulation result between wheeled and legged modes
4.2 自适应步态
自适应步态的仿真在高低不平的地形上进行,在未知地形且没有导航定位的条件下,机器人利用该自适应步态进行探索性的行走。机器人的机身期望高度设计为0.3 m,最大步长为0.1 m。自适应步态的仿真如图15所示(一次六足支撑状态到下一次六足支撑状态)。
图15(a)表示机器人在一个六足支撑状态并且确定了新的支撑平面。机器人将以该支撑平面作为基准,刷新机器人的虚拟支撑平面和机身位姿,此时不需要全局地图的信息。机器人根据新的虚拟支撑平面,可以重新规划新的期望姿态,该姿态平行于3个立足点形成的支撑平面,从而保证了机器人的工作空间的最大性。从图15(a)到图15(b),机器人机身的位姿在指数坐标下进行规划,与此同时,机器人的3条摆动分支依照设计的运动规划寻找可行的立足点。当机器人机身稳定到达期望位姿并且3个摆动分支寻找到稳定的支撑点后,进入图15(c)即机器人的下一个六足支撑状态。

图15 自适应步态仿真Fig.15 Simulation of adaptive gait
在虚拟坐标系下,机器人的机身位姿指数坐标和足末端的位置高度如图16和图17所示。由图16可以看出机器人机身的位姿变化分为3个阶段:刷新虚拟支撑平面阶段、指数坐标系下的运动规划阶段和等待3条摆动腿寻找稳定支撑点阶段。可以看出,机身位姿在指数坐标系下的运动规划阶段是连续平稳的。利用指数坐标的运动规划减少了机器人机身由于速度突变带来的惯性力,使得机器人的运动更加平稳。机器人在指数坐标系下,不仅可以使用三次曲线进行拟合运动规划,也可以使用其他的曲线进行拟合,如正弦曲线等。如图17所示,机器人立足点高度在一定程度上能够体现地形的起伏变化,通过立足点的位置,可以建立简单的地形离散图,用以记录当前地形的离散特征。该仿真验证了自适应步态在没有视觉和环境地图下的可行性。由视频仿真可以看出,在地形起伏过大的情况下某个摆动分支无法(在工作空间内)搜索到立足点,机器人在重力作用下产生倾斜,保证未搜索到立足点的分支与地面接触。当机器人遇到较大的坑状地形后,可能产生倾倒或者颠覆,此时机器人可使用倾倒恢复的运动规划进行恢复。

图16 自适应步态仿真的指数映射Fig.16 Exponential mapping of adaptive gait simulation

图17 自适应步态仿真的足末端位置高度Fig.17 Foot end height of adaptive gait in simulation
4.3 倾倒恢复运动
机器人的倾倒恢复运动仿真如图18所示。由仿真可以看出,机器人自适应步态行走过程中遇到大坑的情况下发生倾倒,机器人在倾倒后进入构型S1的状态,并依靠重力和机身的形状特点使机器人保持稳定的状态,按照所提出的运动规划方法恢复足行状态。

图18 倾倒恢复仿真结果Fig.18 Simulation of recovery after stumble
5 结 论
针对星球探测的复杂环境,设计了一种具有高度对称性的六足轮腿机器人。
1) 相对于典型的中心对称六足轮腿机器人,该机器人的结构还具有关于机身水平面对称的特性,同时膝关节采用双平行四边形机构传动,消除了现有足式机器人膝关节平行四边形机构的奇异位置,实现了膝关节关于大腿的对称运动。该机器人在星球着陆、倾倒恢复、空间站舱壁移动等特殊情况下,可以直接交换机身的上下面进行运动规划,避免了由于机身的方向性带来的复杂运动规划,使机器人具有更好的适应性。
2) 设计了一种基于指数坐标在SE(3)空间规划的自适应步态。机器人可利用该步态在没有局部地图和视觉等特殊境况下依靠机身的惯性测量单元和足底力传感器实现连续稳定的行走。由于机身基于指数坐标在SE(3)空间进行运动规划,该方法在位姿空间没有奇异性,能够更好地实现连续运动。
3) 提出了一种倾倒恢复的策略。该机器人利用关于机身水平面对称的特性,可以直接改变机身的上下面,实现倾倒恢复。
提出的自适应步态以三角步态为基础,在一定程度上限制了机器人的灵活性。具有更加灵活的自由步态将作为该机器人未来的研究内容,使该机器人在星球探测的复杂未知环境中具有更好的适应性。

