江津观音岩长江大桥减震分析

王亚欣 李武生 王贵春，* 张世蒙

（1.郑州大学土木工程学院，郑州450001；2.机械工业第六设计研究院有限公司，郑州450007）

0 引 言

随着半漂浮斜拉桥跨度的逐渐增大，桥梁结构的主梁和主塔地震响应位移也往往随之增大。在强震作用下，过大的主梁位移会导致伸缩缝发生破坏、主梁与邻跨引桥发生碰撞导致落梁等破坏［1-2］。因此，为解决强震作用下大跨度斜拉桥主梁纵向位移过大而引发碰撞及落梁等问题，分析桥梁结构的地震响应进而采取合理有效的减震措施具有重要意义。

近年来，关于桥梁减震措施的研究得到学者们的广泛关注［3］。李小珍等［4］以武汉二七长江大桥为例，研究了附加液体黏滞阻尼器对大跨度斜拉桥抗震性能的影响，得出了阻尼器的最优参数。张文学等［5］系统研究了不同桥面相对高度下黏滞阻尼器对斜拉桥地震响应的减震效果，得出桥面相对高度是影响黏滞阻尼器最优参数及减震效果的重要参数。史俊等［6］以漂浮体系斜拉桥为研究对象，分析了地震波特性对黏滞阻尼器控制效果的影响。Camara等［7］采用金属阻尼器作为减震装置来控制斜拉桥的地震反应，研究发现金属阻尼器对斜拉桥的地震反应起到较好的控制效果。沈星等［8］提出了一种钢阻尼器与滑动支座组合的边墩新型横向减震体系，并通过有限元分析验证了该体系具有显著的减震效果。目前，关于大跨度斜拉桥减震措施的研究多采用黏滞阻尼器，而关于软钢阻尼器在大跨度斜拉桥的减震中的应用相对较少。软钢阻尼器具有良好的耗能能力和抗疲劳性能，其对半漂浮斜拉桥体系的减震效果有待进一步研究。

以江津观音岩长江大桥为研究对象，采用有限元软件ANSYS 建立大跨度斜拉桥有限元模型。在分析其动力特性的基础上，对大跨度斜拉桥进行非线性时程分析，并与塔梁固结体系进行对比。此外，分别研究了采用黏滞阻尼器和软钢阻尼器控制大跨度斜拉桥结构地震响应的最优参数值，并对比了两种减震装置选取最优参数值对江津观音岩长江大桥地震位移响应的控制效果。

1 分析模型

江津观音岩长江大桥为一座纵向半漂浮体系斜拉桥，主跨为（35.5+186+436+186+35.5）m，主塔为菱形结构，滴水岩侧和南彭侧桥塔高度分别为167.29 m 和172.79 m。其中滴水岩侧桥面上塔柱高111.56 m，桥面下塔柱高61.23 m，南彭侧桥面上塔柱高111.56 m，桥面下塔柱高55.73 m。参考文献［5，9］的研究表明，桥面相对高度是影响阻尼器减震效果的重要参数，并采用桥面相对高度系数β（桥面下塔柱高度与索塔全高之比）表征。本桥滴水岩侧和南彭侧桥面相对高度系数β 分别为0.33和0.35。

采用有限元软件ANSYS 建立鱼骨式斜拉桥分析模型，主梁、主塔及桥墩采用Beam188空间梁单元模拟，拉索采用空间杆单元Link10 模拟。模型考虑斜拉索垂度效应的影响，并采用Ernst公式对拉索弹性模量进行修正。采用Combin14 弹簧单元模拟桩土相互作用，并根据《公路桥涵地基与基础设计规范》（JTG D63—2007）［10］给出的“m”法计算土的弹簧刚度。桥梁分析模型如图1所示。

图1 有限元分析模型Fig.1 Finite element analysis model

2 结构动力响应分析

2.1 地震波选取

根据《公路桥梁抗震设计细则》［11］中的建议，选取2 条天然地震波（El Centro 波和Taft 波）和1条人工地震波进行计算，并对计算结果进行分析。进行三向时程分析时，三个方向的峰值加速度比值为ax：az：ay=1：0.85：0.65，调整地震波加速度峰值为0.2 g。

2.2 自振特性分析

对半漂浮体系和塔梁固结体系进行动力特性分析，得到结构前6 阶自振频率及振型如表1 所列。由表1 可知，同阶的自振频率，半漂浮体系的通常较小。半漂浮体系的一阶自振频率为0.091 Hz，为固结体系的28.5%。由于半漂浮体系纵向塔梁之间无约束作用，结构纵向刚度最小，一阶振型对应于主梁纵向振动，而塔梁固结体系，纵向刚度较大，一阶振型表现为主梁对称侧弯。

2.3 地震响应分析

对半漂浮体系和塔梁固结体系，分别输入El-Centro 波、Taft 波和人工波进行非线性时程分析，得到关键截面的最大响应结果如表2 所示。由表2 可知，在人工波作用下关键截面的地震响应值大于El Centro 波和Taft 波作用下的情况，故采用人工波输入下的计算结果对比半漂浮体系和塔梁固结体系地震响应规律的差异。结构在人工波下的地震响应时程如图2所示。

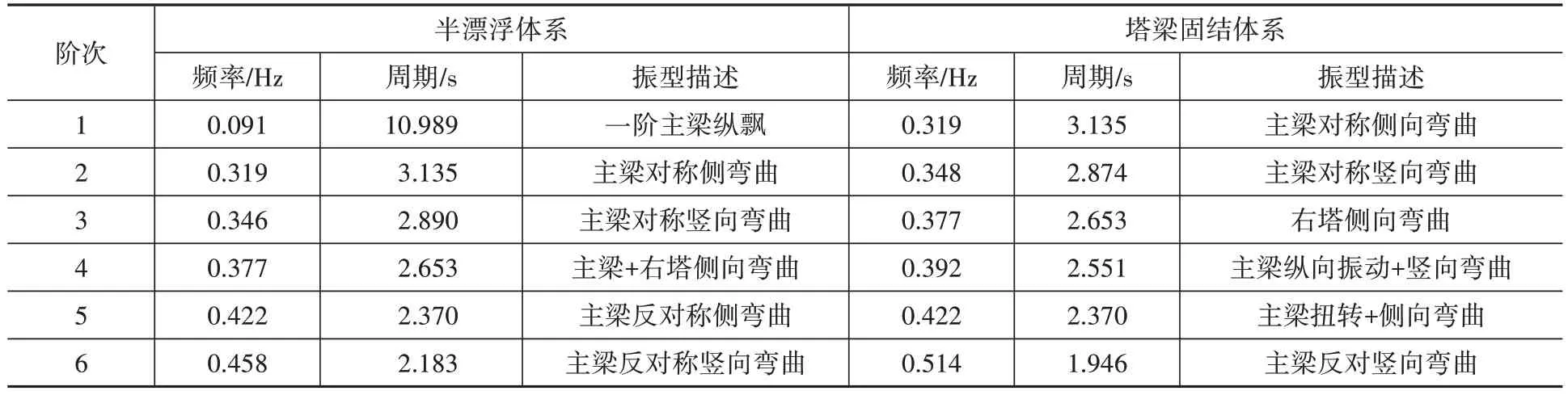
表1 自振频率与振型Table 1 Natural frequency and mode

图2 半漂浮体系与塔梁固结体系地震响应对比Fig.2 Seismic response comparison between semi-floating system and tower beam consolidation system

表2 关键截面地震响应最大值Table 2 Maximum seismic response of key sections

由图2和表2可知：两种结构体系的梁端纵向位移与塔顶纵向位移变化趋势基本一致，而塔顶位移略大于梁端位移；半漂浮体系的响应较大，其梁端位移和塔顶位移分别为塔梁固结体系的3.7倍和3.5 倍；塔梁固结体系虽然位移较小，但其结构受力较大，塔梁固结体系的塔底剪力和弯矩分别为半漂浮体系的2.7倍和1.4倍。

由上述自振特性和地震响应分析可知，塔梁固结体系的结构刚度较大，自振周期较小，位移响应可得到有效的抑制，但塔底剪力和弯矩较大，对整个结构的内力控制不利；而半漂浮体系的结构刚度较小，振动周期长，结构内力大幅减小，但结构位移较大，对结构的位移控制不利。因此，对于斜拉桥结构，在选用半漂浮体系时应采用有效的减震控制措施对结构的位移进行有效的抑制。

3 桥梁减震分析

采用黏滞阻尼器和软钢阻尼器对半漂浮斜拉桥结构体系的位移响应进行控制，沿桥梁纵向在每个主塔横梁与主梁之间对称布置4 个阻尼器，共8个，如图3所示。

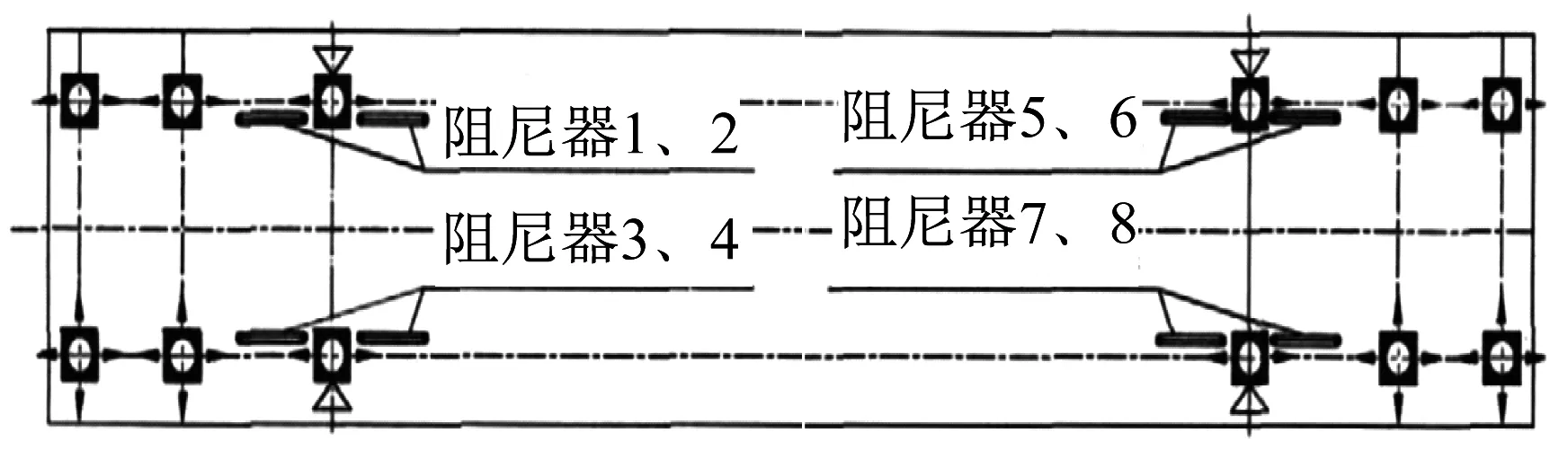
图3 阻尼器布置Fig.3 Damper layout

3.1 减震装置模拟

3.1.1 黏滞阻尼器

根据桥梁用黏滞流体阻尼器，黏滞阻尼器的计算模型为

式中：Fd为阻尼力；c为阻尼系数，与阻尼器的具体构造有关；α为速度指数，其值介于0.2～1 之间；V为阻尼器相对速度。

在ANSYS 中可采用Combin37 单元模拟黏滞阻尼器，如图4 所示。Combin37 单元为非线性一维单元，由2 个活动节点（I、J）和可选的2 个控制节点（K、L）组成，整个单元的复杂非线性行为主要由控制节点产生，通过输出控制节点相对位移的一阶导数作为阻尼器的速度，来实现黏滞流体阻尼器的功能［4］。

3.1.2 软钢阻尼器

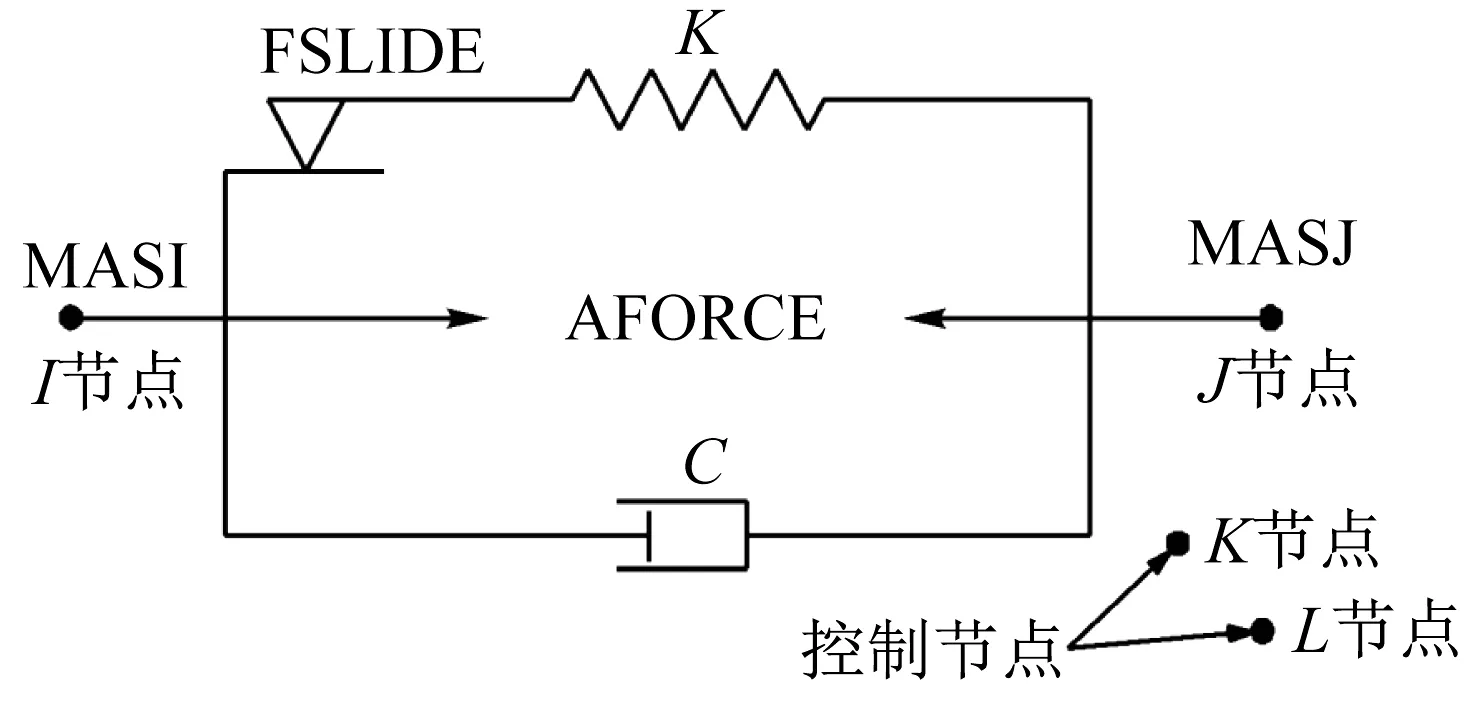
图4 Combin37单元Fig.4 Combin37 element

软钢阻尼器的恢复力模型，可采用双线性模型描述，如图5 所示。其中，Fy为屈服荷载，Δy为屈服位移，Fu为屈服荷载，Δu为极限位移，Ka为屈服前刚度，K1为屈服后刚度。根据阻尼器的力学特性，在ANSYS 中采用Combin40 单元模拟［12］，如图6 所示。其中单元参数设置如下：k1为弹性刚度与屈服后刚度之差；k2为屈服后刚度，FSLIDE设置为屈服荷载；阻尼系数C、间隙GAP和单元质量M均设置为0。

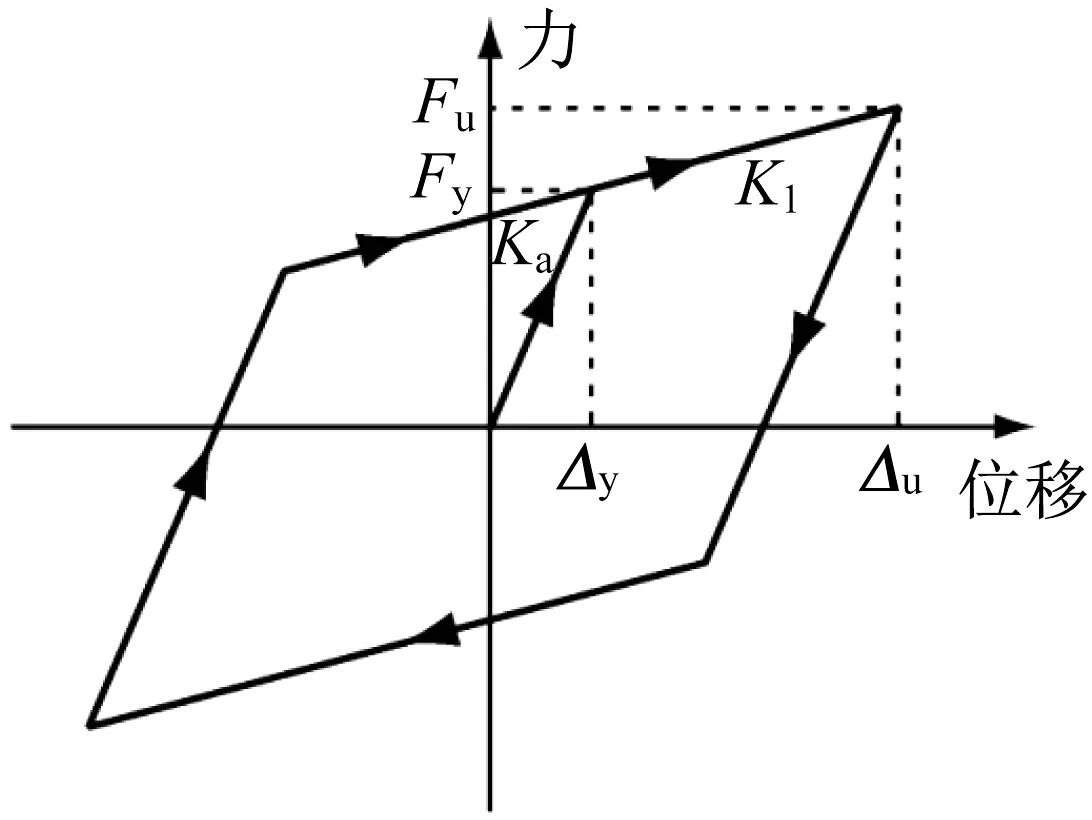
图5 双线性恢复力模型Fig.5 Bilinear restorative force model

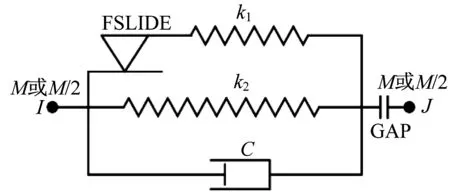
图6 Combin40单元Fig.6 Combin40 element

3.2 减震装置参数优化

3.2.1 黏滞阻尼器最优参数分析

分析不同黏滞阻尼器的阻尼系数和速度指数下结构的地震响应，得到最优阻尼系数和阻尼指数。人工波输入下的斜拉桥地震响应随黏滞阻尼器参数的变化关系如图7所示。

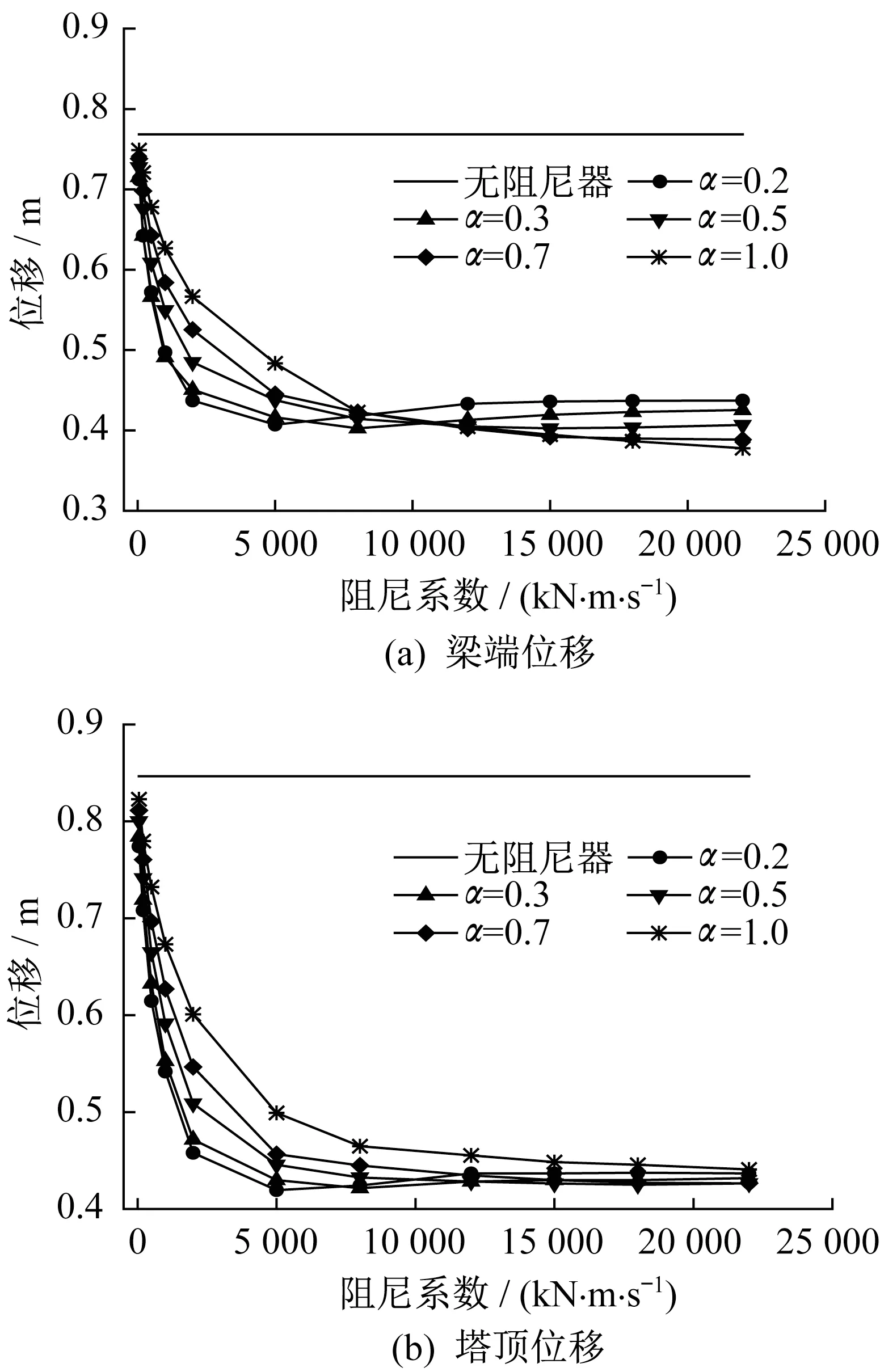
图7 位移与阻尼系数的关系曲线Fig.7 Relationship between displacement and damping coefficient

由图7 可以看出，黏滞阻尼器能显著降低主梁和主塔的位移，在阻尼系数c相同的情况下，速度指数α越小，减震效果越明显。但在速度指数α=0.2 和α=0.3 的情况下，当阻尼系数c＞5000 kN·m·s－1时，主梁与主塔位移基本不再减小，且略有增大。可见采用非线性黏滞阻尼器时，并非阻尼系数越大减震效果越好。由图8、图9可以看出，塔底剪力和弯矩随着阻尼系数的增加呈先减小后增大的变化趋势。与无黏滞阻尼器时的结果相比，低阻尼系数下的阻尼力有利于改善主塔的传力途径，因而塔底弯矩和剪力在阻尼力较小时有短暂的下降趋势。而当阻尼系数较大时，塔梁之间产生相对运动幅度受阻尼器限制，从而使二者的连接形式向着塔梁固结体系过渡，因此塔底弯矩和剪力又逐渐上升。当速度指数α=1，阻尼系数c=5 000 kN·m·s－1时，塔底剪力和弯矩最小，减震效果最明显。比较各种阻尼器系数下结构的内力、位移响应，较为合理的阻尼器参数为：阻尼指数α=0.5，阻尼系数c=5 000 kN·m·s－1。

3.2.2 软钢阻尼器最优参数分析

在塔梁连接处均设置相同参数的软钢阻尼器，其屈服位移Δy为10 mm，极限位移Δu为屈服位移的15倍，极限荷载Fu为屈服荷载Fy的1.15倍［12-13］。

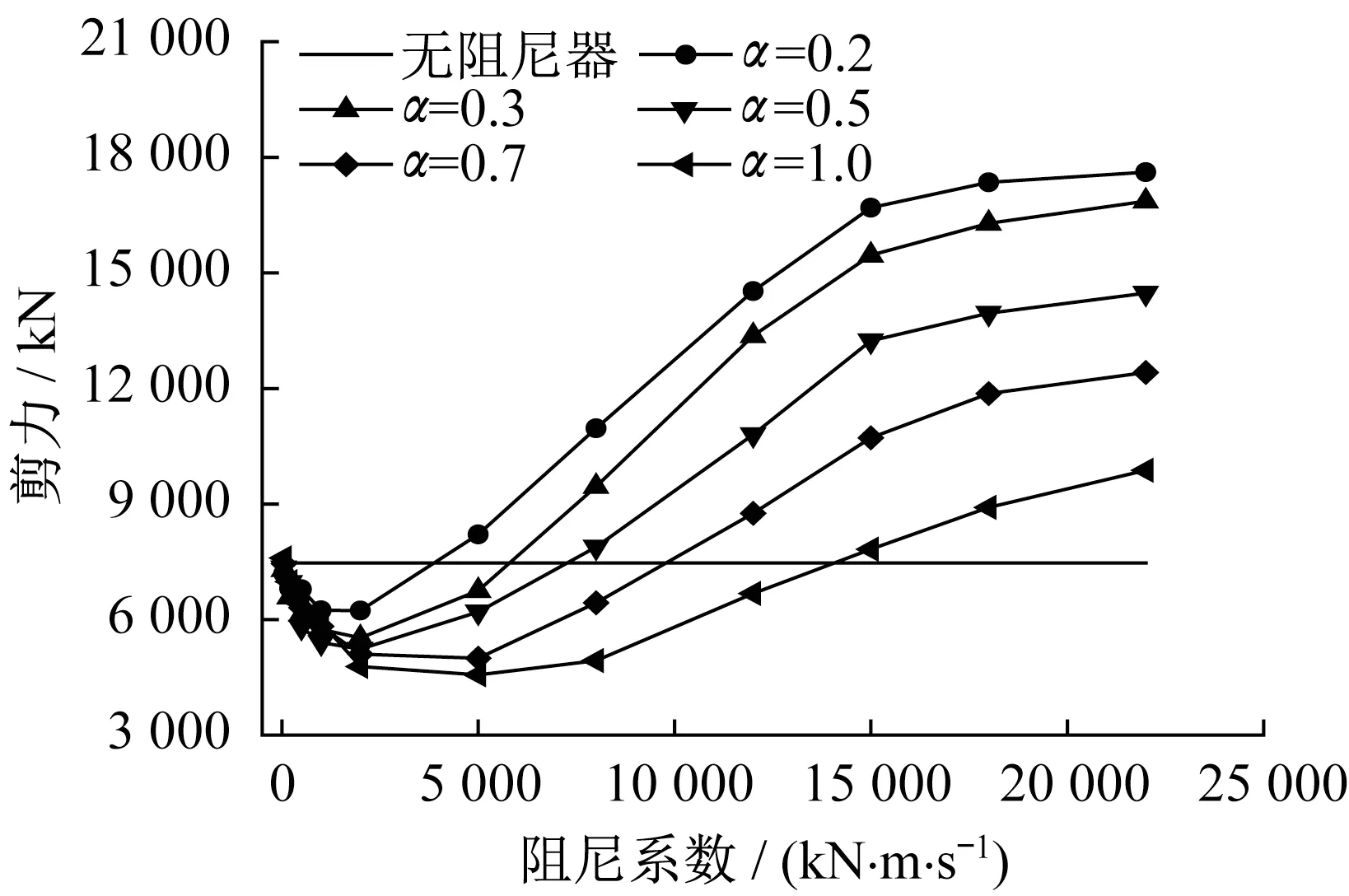
图8 塔底剪力与阻尼系数的关系曲线Fig.8 Relationship between shear force at the bottom of tower and damping coefficient

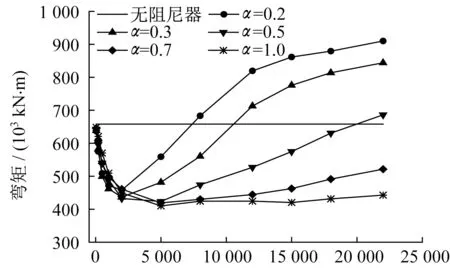
图9 塔底弯矩与阻尼系数的关系曲线Fig.9 Relationship between bending moment at the bottom of tower and damping coefficient

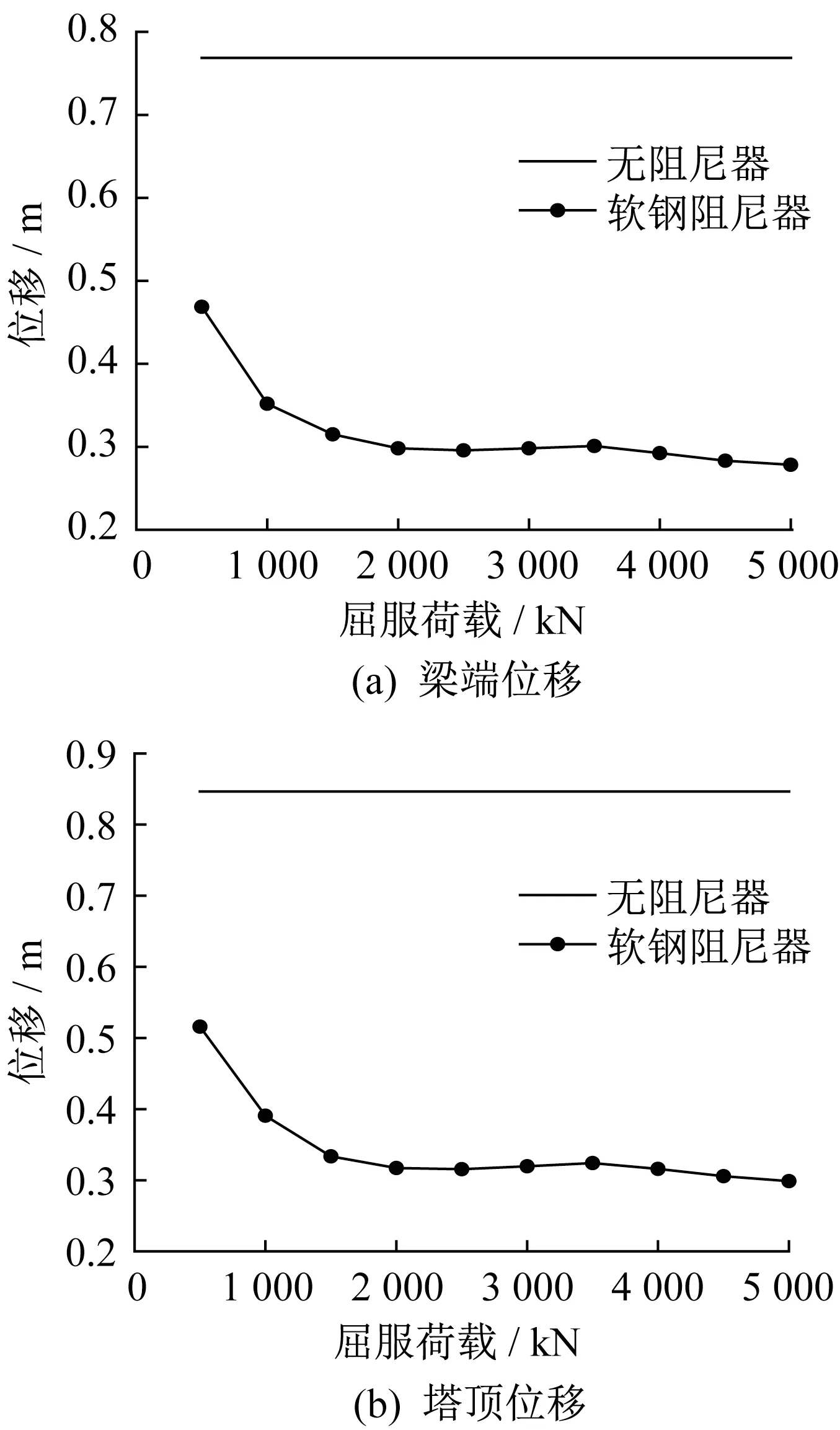
图10 位移与屈服荷载的关系曲线Fig.10 Relationship between displacement and yield load

图11 塔底剪力与屈服荷载的关系曲线Fig.11 Relationship between shear force at the bottom of tower and yield load

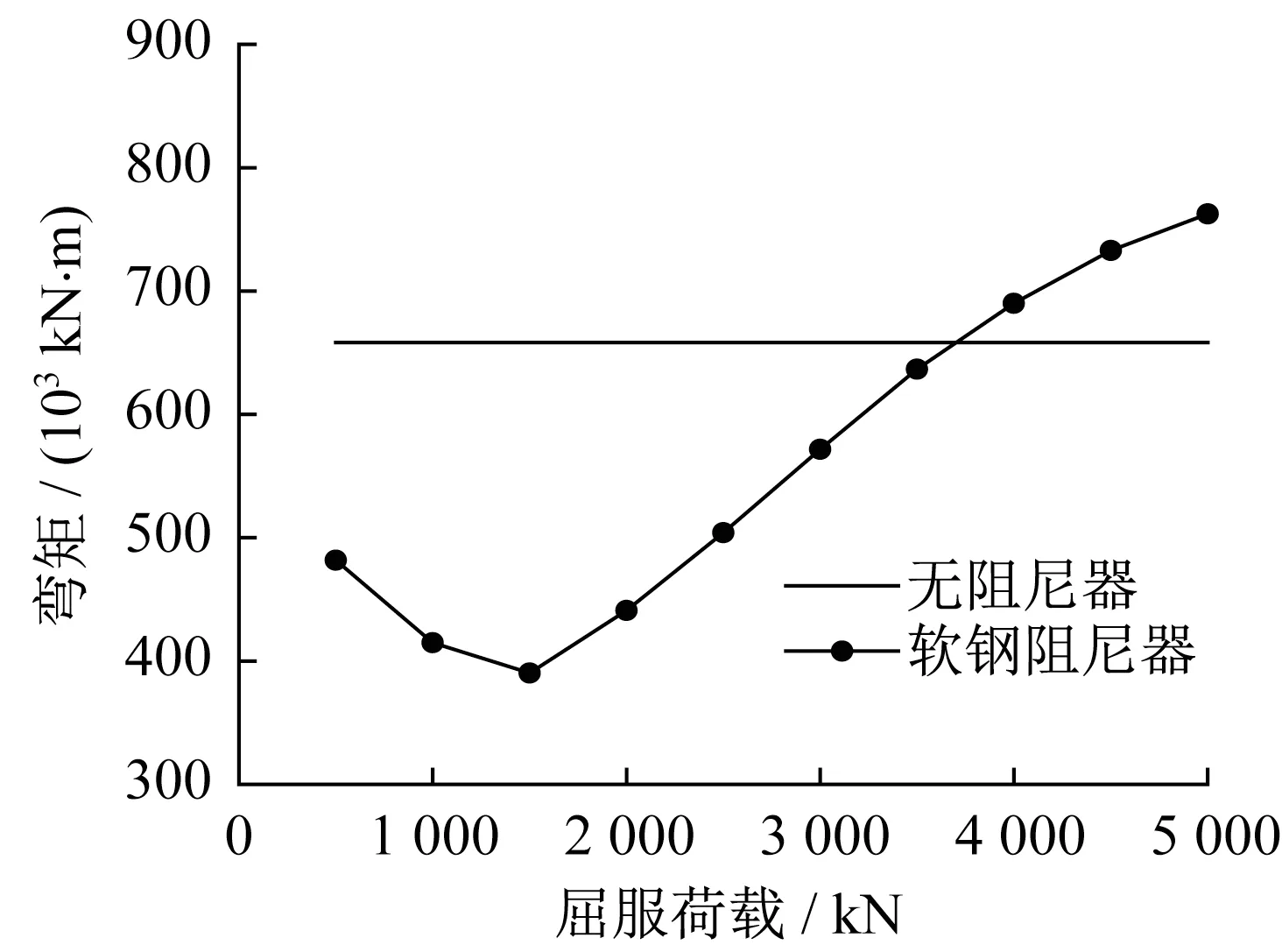
图12 塔底弯矩与屈服荷载的关系曲线Fig.12 Relationship between bending moment at tower bottom and yield load

由图10 可以看出，随着软钢阻尼器屈服荷载的增加，斜拉桥的主梁和主塔位移都有所减少，并且在屈服荷载达到2 000 kN 后，减少趋势逐渐变得平缓。由图11和图12可知，塔底剪力随着软钢阻尼器屈服荷载的增加逐渐增大，当屈服荷载达到3 500 kN后，塔底剪力的增加趋势有所放缓；而塔底弯矩随着屈服荷载的增加先减小后增大，在屈服荷载为1 500 kN时达到最小值。由于软钢阻尼器能够提供较大的抗侧弯刚度，附加的抗侧弯刚度对半漂浮斜拉桥体系的位移控制效果明显，但过大的附加刚度对结构的剪力控制不利。根据软钢阻尼器参数敏感性分析，得到软钢阻尼器的最优屈服荷载为2 000 kN。

3.3 减震控制效果对比

为了更加直观地体现阻尼体系对大跨斜拉桥的减震效果，以无阻尼器的半漂浮体系为基准模型，定义减震率η为

式中，A和B分别为半漂浮体系采取减震措施前后的地震响应峰值。

根据3.2 中的分析结果，分别选取2 种减震装置的最优参数分析其减震效果，如图13 所示。表3 列出了关键部位的响应峰值及相应的减震率。由图13 和表3 可知，两种减震装置均能较好地控制主梁和主塔的位移，其中软钢阻尼器控制效果更好。但采用软钢阻尼器会显著增大主塔塔底剪力，采用黏滞阻尼器对主塔塔底剪力与弯矩有较好的控制效果。

图13 桥梁结构位移时程响应结果对比Fig.13 Comparison of time-history response results of bridge structure displacement

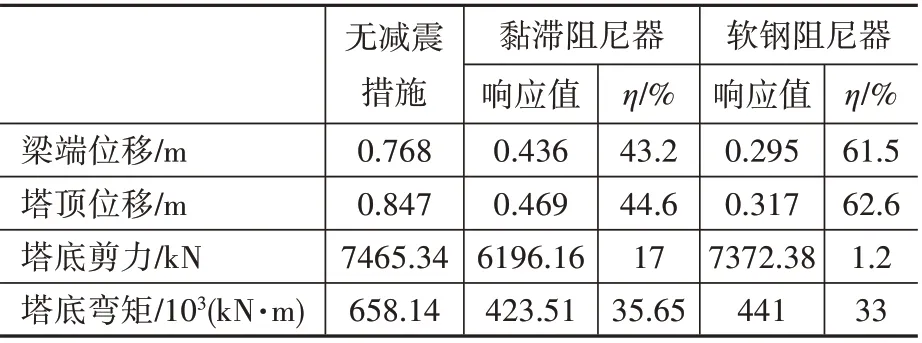
表3 结构关键部位响应峰值及减震率ηTable 3 Maximum response value and aseismic ratio η of key parts of the structure

4 结 论

（1）对于大跨度斜拉桥，采用塔梁固结体系，桥梁结构的地震位移响应较小，但结构内力响应较大；而采用半漂浮体系，可有效降低内力响应，但对桥梁结构的位移控制不利。

（2）两种减震装置均能对大跨度斜拉桥的地震响应起到良好的控制效果，选出每种减震装置适合本桥的最优参数，黏滞阻尼器较为合理的阻尼器参数为：阻尼指数α 为0.5，阻尼系数c=5 000 kN·m·s－1；软钢阻尼器的最优屈服荷载Fy=2000 kN。

（3）在最优参数取值条件下，软钢阻尼器对主梁位移的减震率为61.5%，黏滞阻尼器减震率为43.2%，就位移控制效果而言，软钢阻尼器优于黏滞阻尼器。

（4）两种减震装置均能较好地控制大跨斜拉桥塔和梁的位移，其中软钢阻尼器的减震效果更优，但采用软钢阻尼器会显著增大主塔塔底剪力；采用黏滞阻尼器对主塔塔底剪力与弯矩有较好的控制效果。