亚纯函数涉及重值分担5个小函数结论的改进

谭 洋，刘永奇

(北京师范大学珠海分校应用数学学院，广东 珠海 519085)

0 引言

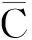
设f(z)，ɡ(z)，h(z)为非常数亚纯函数，a为复常数.如果f(z)-a与ɡ(z)-a有相同的零点，而且每个零点的重数也相同，则称a为f(z)与ɡ(z)的CM公共值；如果不考虑零点的重数，则称a为f(z)与ɡ(z)的IM公共值.类似地，如果f(z)-h(z)与ɡ(z)-h(z)有相同的零点，且每个零点的重数也相同，则称h(z)为f(z)与ɡ(z)的CM公共函数；如果不考虑零点的重数，则称h(z)为f(z)与ɡ(z)的IM公共函数.

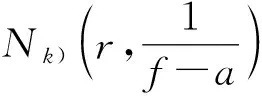
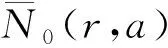
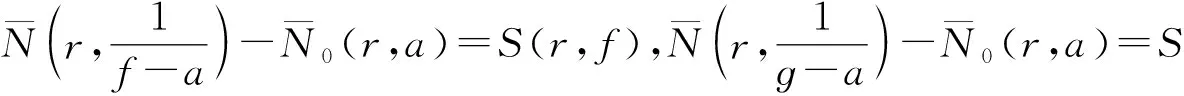
则称a(z)为f(z)与ɡ(z)的“IM”公共小函数.显然若a(z)为f(z)与ɡ(z)的IM公共小函数，则a(z)必为f(z)与ɡ(z)的“IM”公共小函数.

用NE(r，a)表示f(z)-a(z)和ɡ(z)-a(z)具有相同重级的公共零点的计数函数，每个零点仅计1次.如果

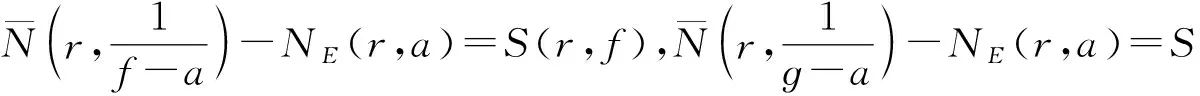
则称a(z)为f(z)与ɡ(z)的“CM”公共小函数.

1929年，Nevanlinna证明了下述著名的五值定理：

定理A[2]设f(z)，ɡ(z)为2个非常数亚纯函数，aj(j=1，2，3，4，5)为C上的5个判别的复数.如果aj(j=1，2，3，4，5)为f(z)与ɡ(z)的IM公共值，则f(z)≡ɡ(z).

Nevanlinna提出下述著名问题：将定理A中常数换为小函数，定理A是否仍然成立？围绕这一问题，许多学者进行了广泛的研究，相关结果可参阅文献[3-6].2000年，李玉华和乔建永[5]得到下面定理：

定理B 设f(z)，ɡ(z)为2个非常数亚纯函数.如果aj(z)∈(S(f)∪S(ɡ))∪{∞}(j=1，2，…，5)为f(z)与ɡ(z)的IM公共小函数，则f(z)≡ɡ(z).

根据定理B的证明，容易得到下面的定理C，它是定理B的简单的推广.

定理C 如果将定理B中IM替换成“IM”，定理B仍成立.

2001年，姚卫红[6]得到下面的结果：

定理D 设f(z)，ɡ(z)为2个非常数亚纯函数.如果存在f(z)与ɡ(z)的5个判别小函数aj(z)(j=1，2，…，5，可有一个为∞)，满足Ek)(aj，f)=Ek)(aj，ɡ)(j=1，2，…，5)，其中k为正整数且k≥16，则f(z)≡ɡ(z).

本文在文献[6]的基础上，应用Nevanlinna值分布理论，对上述定理D的结果进行改进，所得结果进一步丰富了亚纯函数的值分布理论.

1 几个引理

引理1[1]若a(z)为f(z)与ɡ(z)的“CM”公共小函数，则a(z)必为f(z)与ɡ(z)的“IM”公共小函数.

引理2[7]设f(z)为非常数亚纯函数，aj(z)∈S(f)∪{∞}(j=1，2，…，5).则有

这里ε为充分小的正数.

引理3[8]设f(z)，ɡ(z)为2个非常数亚纯函数，且以0，1，∞为“CM”公共值.如果f(z)≢ɡ(z)，则对任意一个f(z)与ɡ(z)的小函数a(z)，只要a(z)≠0，1，∞，有

这里r∈J，mesJ=+∞，r→+∞.

引理4设f(z)，ɡ(z)为2个非常数亚纯函数，aj(z)∈(S(f)∪S(ɡ))∪{∞}(j=1，2，…，5)，kj(j=1，2，…，5)为正整数或∞，且满足k1≥k2≥…≥k5.如果

Ekj)(aj，f)=Ekj)(aj，ɡ)(j=1，2，…，5)，

则有

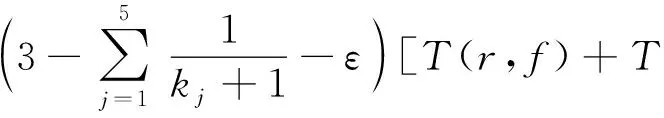
证明由引理2有

即

(1)

类似可得

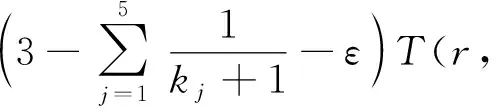
(2)

由(1)和(2)式有

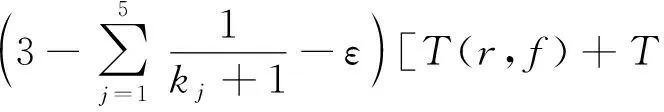
2 主要定理及证明

定理1设f(z)，ɡ(z)为2个非常数亚纯函数，aj(z)∈(S(f)∪S(ɡ))∪{∞}(j=1，2，…，5)，kj(j=1，2，…，5)为正整数或∞，且满足k1≥k2≥…≥k5.如果

Ekj)(aj，f)=Ekj)(aj，ɡ)(j=1，2，…，5)，

(3)

且

(4)

则f(z)≡ɡ(z).

证明不失一般性，不妨设a1(z)=0，a2(z)=∞，a3(z)=1，a4(z)=a(z)，a5(z)=b(z).令

其中：

如果H1≢0，则有m(r，H1)=S(r，f).下面估计N(r，H1)：

注意到

所以有

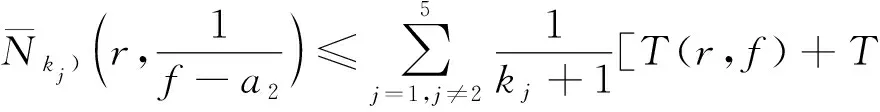
(5)

令

其中：

令

其中：

令

其中：

令

其中：

如果Hj≢0(j=2，3，4，5)，同样可以得到：

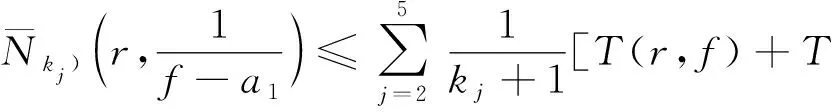
(6)

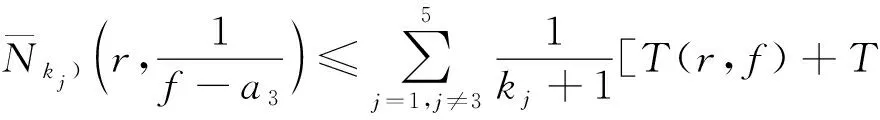
(7)

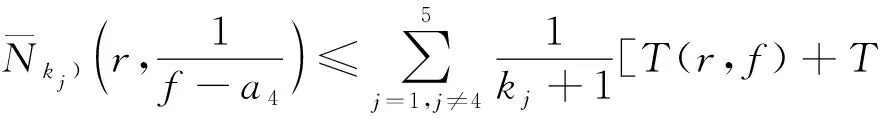
(8)

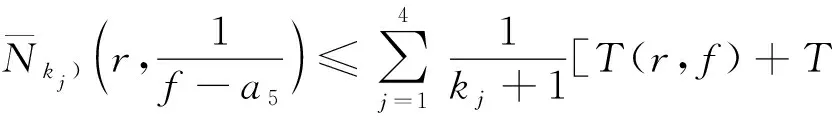
(9)

由(5)—(9)式可得

(10)

由(3)式同样有

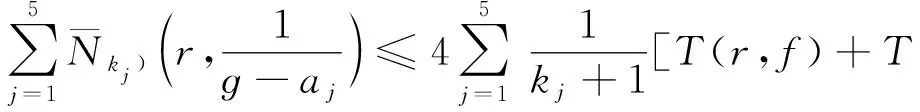
(11)

由(10)和(11)式得

(12)

由引理4和(12)式有

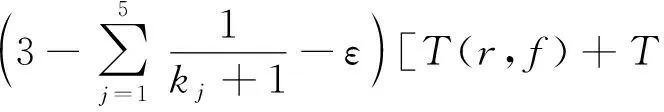
即

(13)

其中ε为充分小的正数，在不同地方可能不同.由条件(4)可知(13)式矛盾.因此，Hj(j=1，2，…，5)中至少有一个恒为零.不妨设H2≡0，则f(z)和ɡ(z)以0，1，∞，a(z)为“CM”公共小函数.由定理1的条件和引理3可知，f(z)和ɡ(z)以0，1，∞，a(z)，b(z)为“CM”公共小函数，则由定理C和引理1可得f(z)≡ɡ(z).同理，当Hj≡0(j=1，3，4，5)时亦有f(z)≡ɡ(z).

定理2设f(z)，ɡ(z)为2个非常数亚纯函数，aj(z)∈(S(f)∪S(ɡ))∪{∞}(j=1，2，…，5)满足Ek)(aj，f)=Ek)(aj，ɡ)(j=1，2，…，5)，其中k为正整数且k≥15，则f(z)≡ɡ(z).

证明在定理1中取k1=k2=…=k5=k即可得证.