巧设关联性习题 训练结构化思维——以《观察物体》练习课为例

（福建师范大学附属小学，福建 福州 350007）

培养学生的数学核心素养主要从“优质的数学情感模式（感性经验系统）、良好的数学思维品质（理性思考系统）以及相应阶段清晰完整的数学认知结构”这三个方面进行［1］，这里的数学认知结构也是数学核心素养的内在表现。

学生个体的数学认知结构主要包括：个体的数学知识结构、数学思想方法、元认知、非智力因素等。［2］要想建立清晰完整的数学知识结构，离不开结构化思维训练。“结构”所指向的是事物内部各个构成之间的组建方式，“结构化思维”则是以事物内部结构为对象而展开的探寻过程，从而把握事物内部各个构成之间的关系，并从中提炼出一般规律。［3］结构化思维的学习，能让学生触及事物的本质和核心，思考更为清晰和高效，有效地运用数学思维去思考和解决生活中的实际问题。

但是，目前小学数学练习课中，碎片化教学是比较常见的一种状况，有些教师仅仅进行习题的堆积练习和就题讲题。对学生的学习情况进行调查后发现：碎片化教学中学生对于局部知识的理解相对较好，但是对于整体框架的构建，自主联系各个知识之间的意识和能力都比较缺乏，无法形成结构化思维。下面笔者就以人教版四年级下册《观察物体》（练习课）为例，针对练习课谈谈如何巧设关联性习题，架构习题间的关联，从而达到结构化思维的训练目的。

一、习题动态变化，架构关联，推进结构化构建

平时的练习课，大多数采用叙述性的教学方式，练习方式缺少灵活性和实践性，很难加深学生对于知识的理解和练习的热情。教师可以通过多媒体展示具有动态变化的练习题目，架构习题间的联系，让孩子感受变中的不变，在激发学生自主探究热情的同时，推进结构化的建构。

例如，首先通过5 个小方块的动态组合，形成了一个几何体（图1），让孩子们判断这些形状是从哪个面看到的。借助“方块塔”软件进行演示、验证。接着把第一层的一个小方块移动位置（图2），继续判断每个面看到的形状。然后在原来的这个几何体上去掉一个小正方体（如图3），观察后在方格图中画出它每个面看到的形状。最后小结：在刚才一系列的观察中，你能说说从不同的方向观察物体有什么注意事项吗？

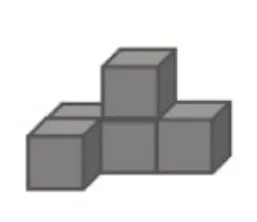
图1

图2

图3

这组题目的目的都是考察学生从不同位置观察几何体的形状。教师通过组合、移动、替换、减少等系列活动，让题和题之间有了动态的变化，学生在这种动态的情境中学习兴趣盎然，同时在变化中构建起从不同方向观察物体的基本方法。

二、习题递阶对比，架构关联，内化结构化理解

在小学数学课堂教学中，对比性题组练习是架构习题间联系的一种常见方式。设计具有递阶性的题组练习，将原理、规律和技能纵横联系于题组之间，引导学生对题组进行对比、思考。在这个过程中，学生数学思维的发展由浅入深，层层深入，体现题组间的逻辑性，有助于帮助学生内化知识的理解，形成思路和技能，从而搭建结构化的知识体系。

例如，课堂上提出这样一系列问题，如果想在这个几何体（图3）上加上一个小正方体。（1）怎么加上面看到的形状不变？（2）怎么加前面看到的形状不变？（3）怎么加左面看到的形状不变？（4）观察所有的方案思考，怎么加才能确保加上一个正方体后，某个固定的面的形状不会发生变化呢？

这种按照一定逻辑结构设计的多层次、多角度、多方位的题组练习，沟通了知识的内在联系，满足了不同层次学生的思维需求。学生可以通过操作、观察、表达、反思等过程找到规律，提炼出“确保某个固定面形状不变”的方法。这样的过程，学生构建了认知网络，内化结构性的理解，提高解决实际问题的能力。

三、问题引导操作，架构关联，促进结构化理解

弗赖登塔尔说过：“数学来源于现实，高于现实。”学生年龄虽小，但具备一定的生活经验以及将经验转化为解决问题策略的能力。学生亲自或间接经历活动过程从而获得的经验，对知识意义的构建才更为有效。［4］对于一些比较抽象的习题，通过实际的操作，积累思维的表象和活动的经验，再引导学生将经验进行加工，找到活动经验与数学之间的联系，把它作为想象的脚手架，从而达到促进结构化理解的目的。

例如，（图4）提供从不同位置观察同一个物体所看到的图形。我们可以分成两个层次提出要求。（1）根据要求，动手尝试操作。

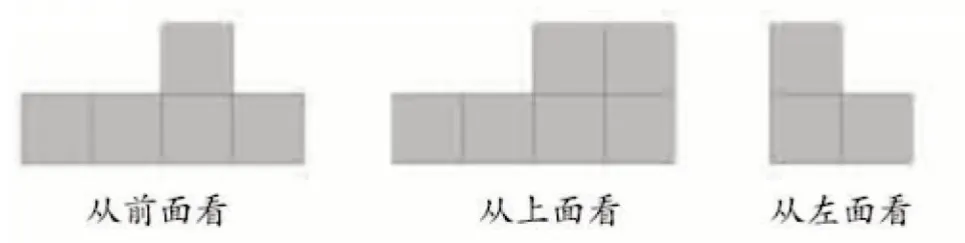
图4

（2）如果不摆，你能根据示意图直接想象吗？

这种习题学生需要多次的试错，才能在尝试中慢慢成功。为了帮助学生理解，我们将搭方块的过程想象成盖房子的生活情景，根据口诀“俯视打地基、正视疯狂盖，左视拆违章”，按照一定的顺序进行拼搭，思维变得有序，拼搭也变得简单。进入第二个问题的时，学生可以再次借助刚才操作中盖房子这个模型进行思考。同一个情景、同样的习题、不同的要求，学生从无序操作—有序操作—利用经验想象，这个过程搭建了习题与操作经验的关联，实现二维和三维的转化，进行了结构化的思考和结构化理解的训练，学生的空间想象力也得以培养。

四、习题多样开放，架构关联，优化结构化思维

学生是存在个体差异的，一节练习课更应该关注到学生的差异，所提供的习题应让所有的孩子的数学思维有所发展。因此设计的习题要求应该适度开放，解决问题的策略允许多样化，留足自主交流的空间，针对学生学习过程中存在的知识障碍和思维障碍，放慢进程，给予学生适度思考、充分交流的机会，辨析明理的空间，启迪学生思考、研究、寻找解决问题的策略。

例如：这个组合体有几个小方块？（图5）

要求：1.不操作，看图想象，可以适当地做标记。

2.独立思考后，在小组内进行交流，选择本组内大家最喜欢的方法进行汇报。

3.思考：这些最受欢迎的方法有什么共同点？

图5

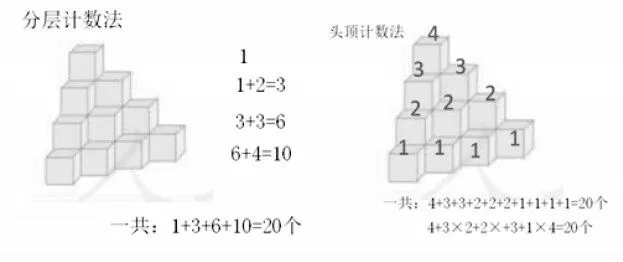
图6

根据正方体拼搭的组合体来想象实际结构，这需要学生综合运用想象、分析、推理等方法。由于难度大，学生的思维方式不同，呈现的解决问题的方法也有较大的区别。独立思考之后的交流，让学生感受到解决问题策略的多样化。在交流中，两种方法（图6）很快地就被大家接受。再次对比两种方法，很快地找到它们的共同点：按一定的顺序（分层或者分列）数小正方体方块。解决问题的策略得以简化，思维也能以结构化的方式进行优化。

五、导图整理总结，展示关联，提升结构化能力

帮助学生构建知识结构有一种重要思维工具——思维导图。［5］思维导图也是有结构的，它像张网把看似分散的点，也就是关键词，连成线、形成面。练习课也应该帮助学生从整体把握和展示知识、问题、方法之间的内在关联，引导学生自己建构知识网络，形成结构意识，促使学生在知识的迁移中实现结构化思维的提升。

例如，练习课快结束前，让学生一起回顾本节课大家是怎样观察物体的，在梳理过程中，形成思维导图。（如图7）

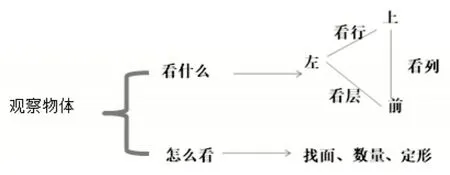
图7

综上所述，巧设动态变化、递阶对比、操作实践、多样开放的习题，借助导图进行整理，让知识从零散走向统整，思维从低阶走向高阶，切实进行结构化思维训练，促进数学核心素养形成提升。“以生为本，学为中心”，基于现实问题进行教学，最大限度地解决学生需要解决的问题，体现结构化学习的意义和价值。