机械连接中钉的轴力和剪切力测量传感器

汪厚冰,魏景超,成李南,李新祥,赵荣

中国飞机强度研究所 全尺寸飞机结构静力/疲劳航空科技重点实验室,西安 710065

虽然飞机制造中机体结构的整体化水平越来越高,但是由于机械连接具有能传递大载荷、装配质量稳定性好及便于装配和拆卸等优点,在飞机结构中即便是复合材料结构目前仍广泛使用机械连接的方法[1-5]。即使连接结构承受面内载荷,但由于次弯曲(偏心弯曲)[6-7]的存在,连接中的钉除了承受剪切力,还有轴力。为了准确掌握钉的受力状态并对钉进行失效分析,研究者需要获取钉的轴力和剪切力。

目前主要通过测试方法和分析方法获得钉的轴力和剪切力。钉轴力的测试方法有以下几种：基于垫片式力传感器的测试方法[8],把力传感器做成垫片,使用时套在钉上；超声波法[9],该方法利用声波的速度和传播时间,计算钉的变形量和轴力；传感器法[10],在钉上粘贴应变片(单片),通过测得的应变计算出钉的轴力。钉的剪切力测试方法包括应变片法[11-13]、压力传感器法[14]及载荷传感器法[6,15-18]。应变片法通过在连接板上粘贴应变片,测量钉附近各截面的应变,计算出对应截面的内力,进而推算钉的剪切力及钉载；压力传感器法在钉与连接孔之间布置压力传感器,通过测得的钉与孔挤压力来获取钉剪切力；载荷传感器法在钉的两侧(或四侧)开槽,槽内粘贴±45°的应变花,通过测的应变值确定钉承受的剪切力。

分析方法主要包括有限元方法和经典刚度法。有限元分析方法有以下几类：用梁单元模拟钉,用壳单元模拟连接板[1,19]；用梁单元和解析刚体模拟钉,用壳单元模拟连接板[20-21]；用三维实体单元模拟钉和连接板,并在钉与板、板与板之间多个接触面之间定义复杂的接触关系[22-23]；3种模拟方法建模工作量、复杂程度和收敛难度依次增大,尤其是第3种方法虽能反映连接结构中的间隙、紧力矩、摩擦力等,其计算量和收敛难度大大增加。经典刚度法[24-28]是将钉和连接板简化成弹簧体,利用钉与板的变形协调关系和力的平衡求解钉的剪切力。

上述测试方法中虽然能得到钉的轴力和剪切力,但这些方法均针对钉一个力(轴力或剪切力)测试,不能同时得到钉的两个力。有限元方法可以得到钉的轴力和剪切力,但有限元的分析结果的正确性需要合适的评估方法。目前工程上需要针对连接结构建立合适的有限元模型和分析模型,并能通过试验测试方法的验证。

本文针对连接结构的工程需求,在MIB[6](Modified Instrumented Bolts)的基础上,提出一种能同时获得钉的轴力和剪切力的测量方法,分别对传感器轴力、剪切力的测量结果的线性、重复性及安装位置影响等进行了测试研究,针对使用过程中不同紧力矩对测量结果影响进行了分析。

1 测试原理

单钉单剪是典型的连接结构,见图1,S1～S4为黏贴应变计的4个平面，在拉力F的作用下,钉在剪切面(连接板的搭接面)上的受力情况见图1(c),包括z向的轴力N、y向的剪切力Fy、x向的剪切力Fx、弯矩My、弯矩Mx。这些载荷会在钉的剪切面产生相应的应变,通常钉受到的这些载荷都较小,发生的变形为小变形,满足线性叠加原理。

载荷作用下钉剪切面上的点A、B、C、D四点的应变见图1(c)。其中,剪切力Fx在点A、C处产生的剪切应变为γxz-Fx,在B、D处不产生剪应变；剪切力Fy在点B、D处产生的剪切应变为γyz-Fy,在A、C处不产生剪应变；弯矩Mx在点A、C处产生的正应变为εz-Mx；弯矩My在点B、D处产生的正应变为εz-My；轴力N在点A、B、C、D产生的正应变εz-N。

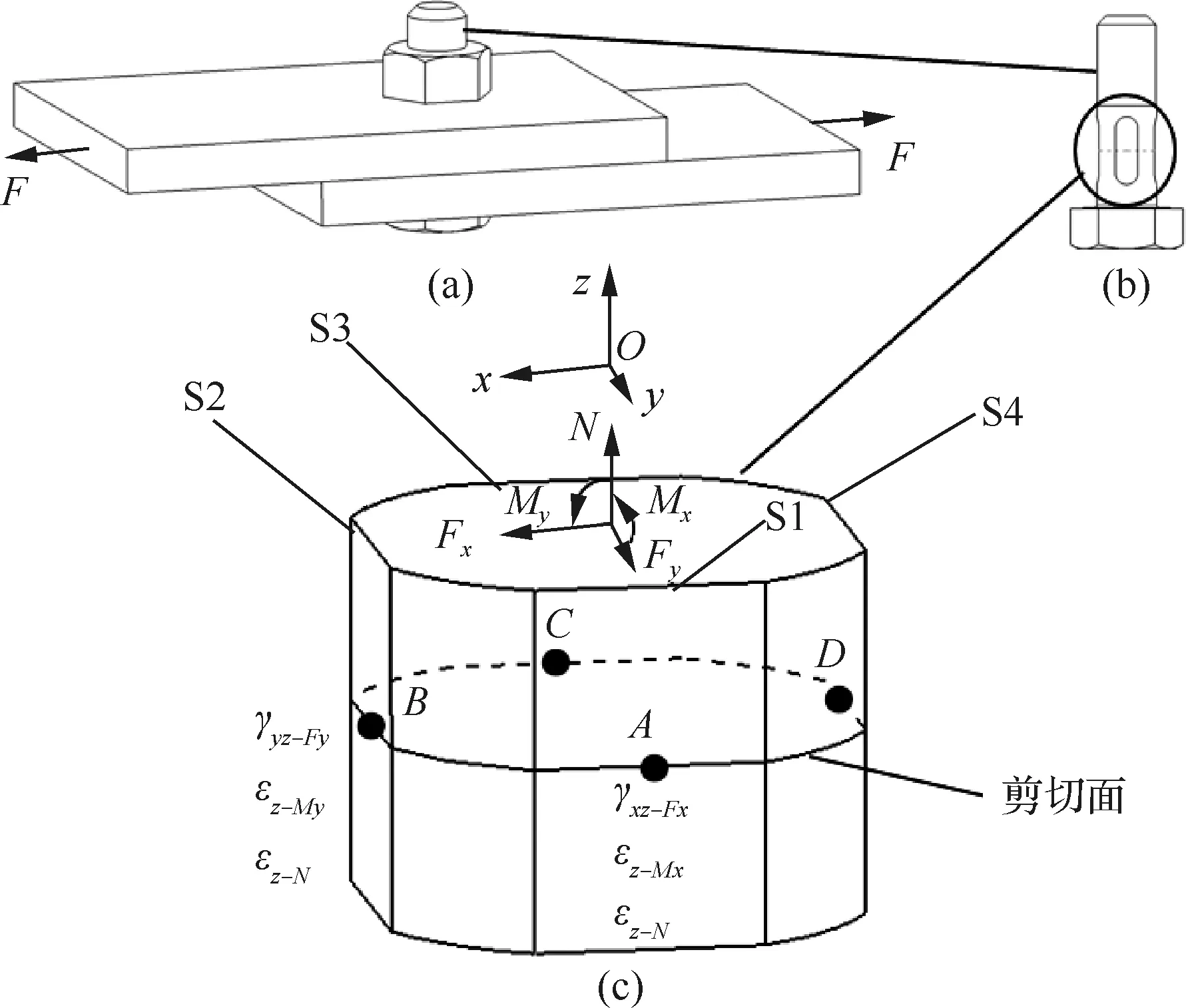
图1 连接结构中钉的载荷与变形Fig.1 Schematic of load and deformation of bolt in joints

根据材料力学的平面应变计算可知,平面内任意方向α的正应变可如下表示：

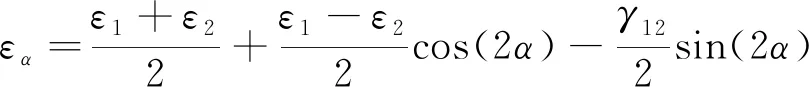
(1)

式中：ε为线应变;γ为剪应变;下标1、2为平面直角坐标系的2个坐标轴。±45°方向的正应变可如下表示：

(2)

根据式(2),剪切面上A点±45°方向上的正应变为

(3)

式中：

(4)

其中:μ为钉的泊松比。

将式(4)代入式(3)可得：

(5)

同理,B点在平面S2内±45°方向的正应变可表示为

(6)

C点与A点背靠背,C点±45°方向的正应变可表示为

(7)

D点与B点背靠背,D点±45°方向的正应变可表示为

(8)

综合式(5)～式(8),剪应变γxz-Fx和γyz-Fy可表示为

(9)

根据虎克定律和力-应力关系,剪切力Fx、Fy可表示为

(10)

式中：G为钉的剪切弹性模量;S为钉的剪切面面积。

由式(3)可得

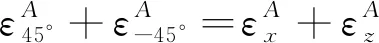
(11)

由式(4)可得

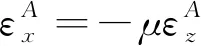
(12)

综合式(11)、式(12)可得S1平面的轴向正应变如下：

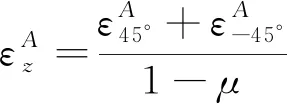
(13)

同理,可得S2平面的轴向应变：

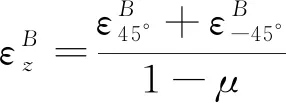
(14)

同理,可得S3平面的轴向应变：

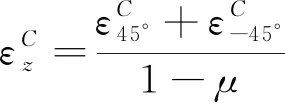
(15)

同理,可得S4平面的轴向应变：

(16)

综合式(13)～式(16),可得钉的平均轴向正应变：

(17)

根据虎克定律和力-应力关系,轴力N可表示为：

N=εzES

(18)

式中：E为钉的弹性模量。

由式(10)、式(18)可知,钉的轴力、2个剪切力可通过测量钉剪切面上的4个点的±45°方向线应变计算得到,根据2个剪切力分量可通过矢量合成方法得到总的剪切力大小和方向。因此,采用钉传感器可得到钉的轴力和剪力。

2 传感器的设计

根据测试原理设计的传感器如图2所示。

图2中传感器的材料为30CrMnSi,直径为8 mm。为了能在传感器上粘贴应变片,根据应变片的尺寸在传感器四周开跑道形槽,跑道形槽沿圆周呈对称分布,且相对于连接板的搭接面对称。每个应变片的中心均与跑道形槽底面中心重合,应变片的中心线与钉的剪切面一致。为了引出应变片的导线(与数据采集设备连接,测量应变片的电阻变化),在每个跑道形槽与传感器头之间加工导线孔,见图2(a)。

由于钉的刚度对钉载及钉的受力状态有重要影响,为了使传感器替换连接结构的钉后,连接结构的受力状态不变,传感器与真实结构的钉具有相同轴向刚度和剪切刚度。飞机连接结构通常采用钛钉,传感器通过开跑道形槽削弱轴向刚度和剪切刚度,使其与钛钉具有相同的刚度。跑道形槽的主要尺寸见图2(a)和图2(b)。

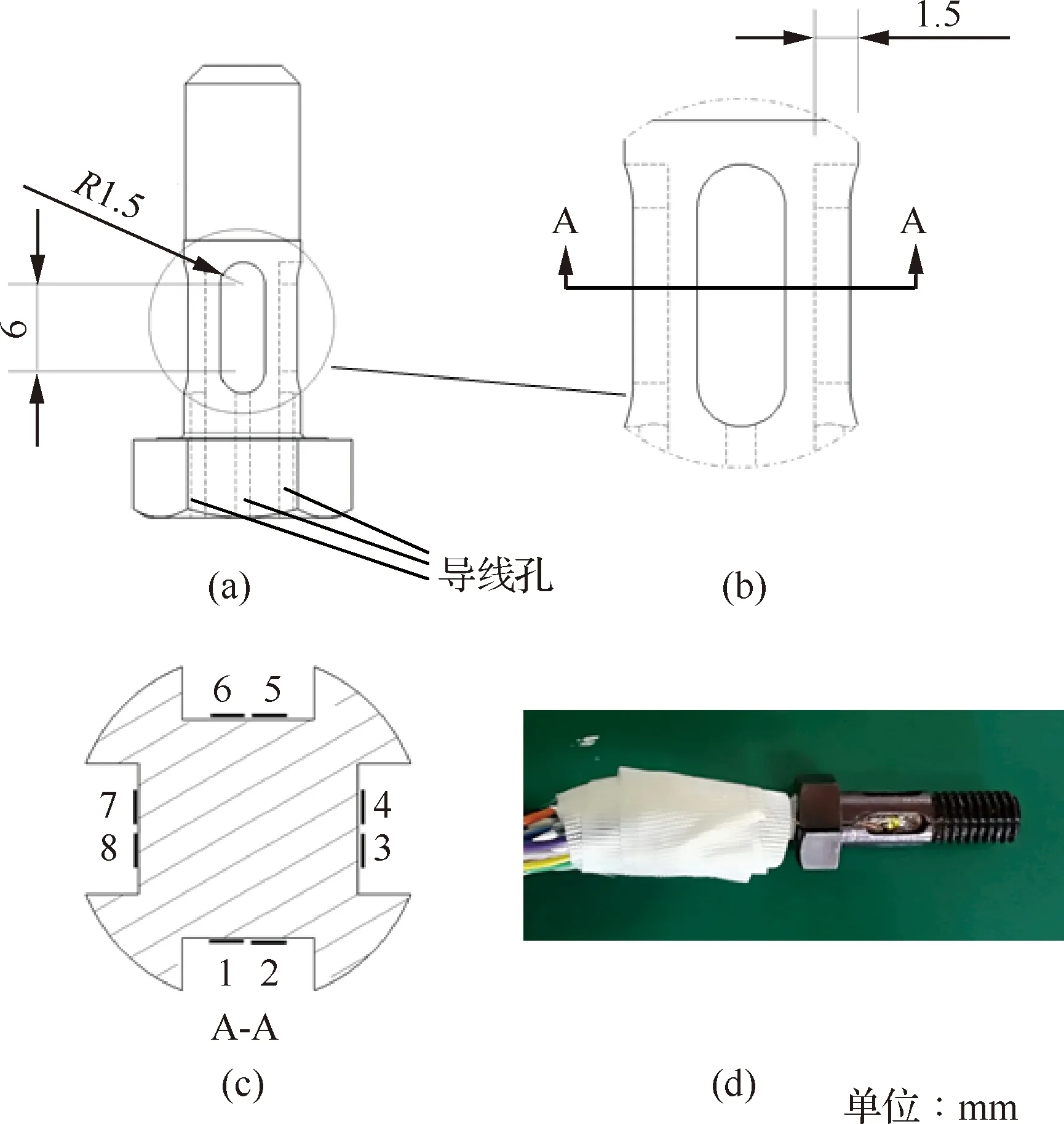
图2 传感器的主要尺寸及应变花的布置Fig.2 Geometry of force sensor and distribution of strain gauge

根据测试原理,每个跑道形槽内布置一个±45° 的应变花,应变花中心与粘贴面中心重合。应变花的布置、顺序及编号见图2(c)。传感器的实物见图2(d)。

3 传感器的测试

作为力传感器,需要满足：载荷-应变的线性关系和测量应变良好的重复性。下面通过对传感器的测试验证其满足上述两方面的要求。

3.1 轴力的测试

为了测量传感器的轴向载荷-应变的关系,设计了一套试验装置,见图3。其中上、下单耳夹持于试验件的夹头中。

把图3的试验装置安装于试验机Instron-8801中,以力控制方式施加拉伸载荷。为了验证传感器的轴向载荷-应变的线性关系及测量应变的重复性,以2 kN为加载级差逐级加载到最大载荷10 kN。试验机的加载相对误差小于示值的0.5%。应变的数据采集设备为ST-24,每级载荷加载到后保载3 s,测量应变,最大载荷级的测量完成后绘制传感器的轴向载荷-应变曲线。由于各零件间可能存在装配间隙,每次试验装置安装后第1次试验结果不采用。第1次试验完成后,卸载,检查设备,保证试验装置及相关试验设备均处于正常状态,进行下一次的试验。此状态的试验完成后,转动传感器约60°,重新试验。共完成5种状态的测试。

图3 传感器的轴力测试装置Fig.3 Axial force test setup of force sensor

传感器的轴力-应变曲线见图4。由图可看出,轴力-应变曲线的线性较好；虽然传感器只受单个拉伸外载荷,但各个应变片的应变并不均匀,其主要原因是由于加工的影响,传感器与上、下单耳贴合并不紧密,导致传感器除了承受拉伸载荷外,还有小的弯矩Mx、弯矩My。

传感器的轴向应变按式(17)计算,5次测试的载荷-轴向应变曲线见图5。由图可见,每次测量的轴向应变的线性良好。虽然传感器的8个应变片测得应变不均匀,但通过式(17)得到的平均轴向应变在各次测试中差异很小,能很好地表征传感器的轴向应变状态。

采用直线方程ε=λN拟合得到5次测试的轴向载荷-轴向应变曲线的斜率λ及线性相关系数R,结果见表1。由表可见,每次测试的轴向载荷-轴向应变曲线的线性相关系数均超过了0.999,表明传感器的轴向载荷-轴向应变的线性相关度很高。5次测试得到的直线斜率的离散系数为0.16%,表明传感器的测试结果重复性好。可以满足传感器对于线性和重复性的使用要求。同时也表明测试结果与传感器的安装角没有关系。

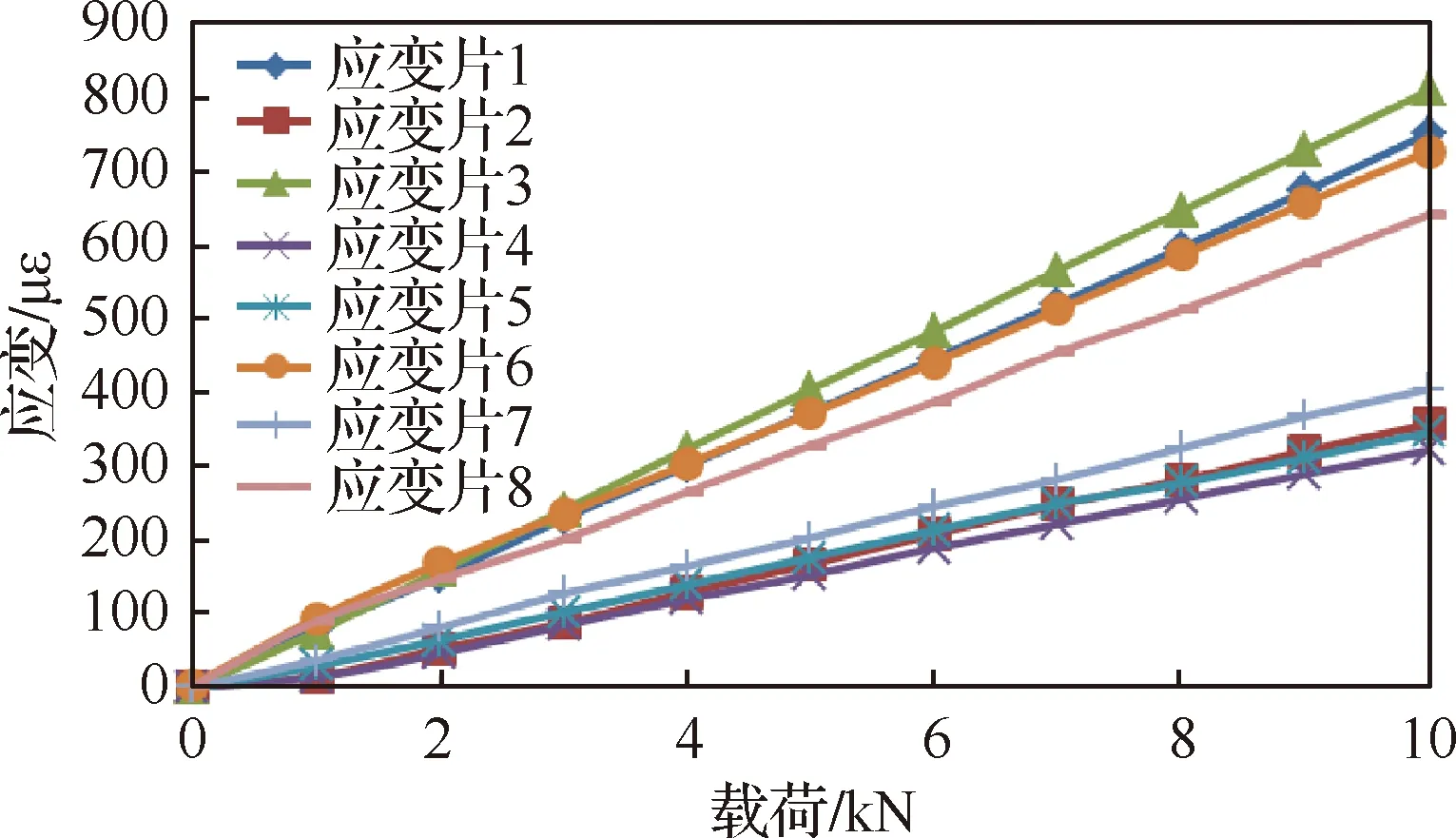
图4 轴力测试中传感器的载荷-应变曲线Fig.4 Load-strain curves of force sensor in axial force test

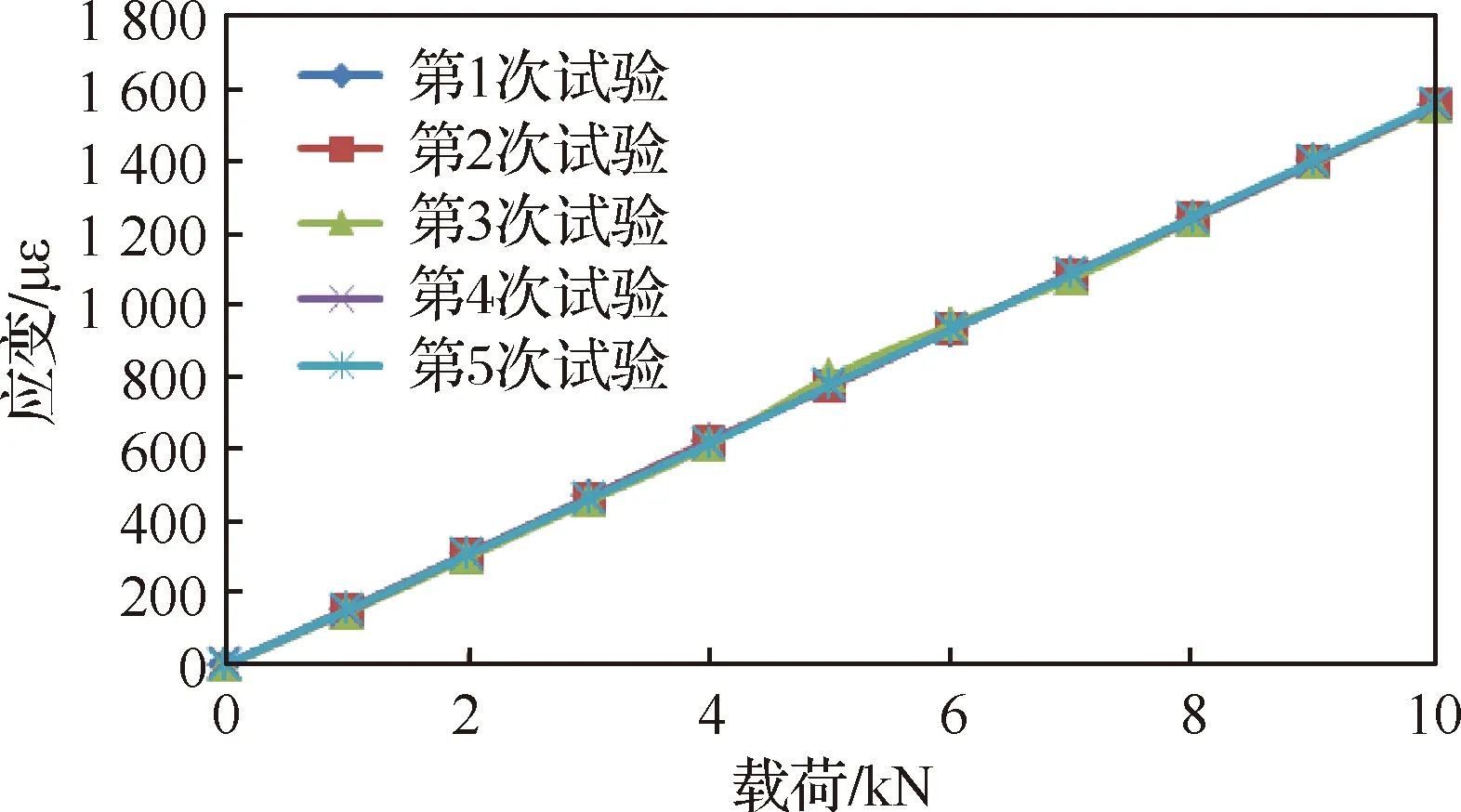
图5 轴力测试中传感器的载荷-轴向应变曲线Fig.5 Load-axial strain curves of force sensor in shear force test

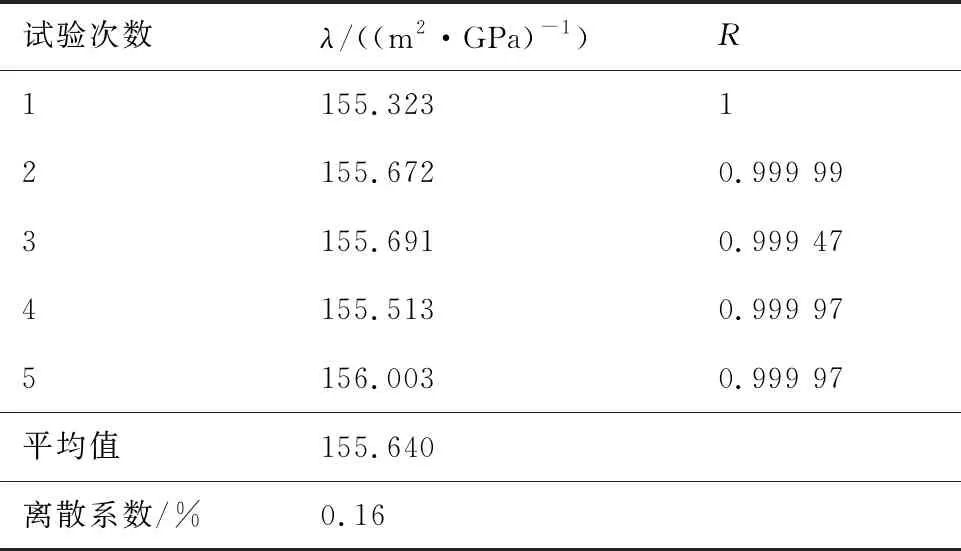
表1 传感器的柔度系数和线性相关系数

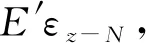
(19)

式中：E′为传感器的弹性模量,取值为200 GPa；面积As为33 mm2,应变εz-N为微应变,拉力N的单位为kN,由此可计算常数λ的理论值约为152,与表1中测试的平均值很接近(误差为2.3%),验证了测试结果准确性和可靠性。

3.2 剪切力的测试

3.2.1 传感器的线性和重复性

传感器剪切力的测试方法见图6。传感器的尺寸见图3。试验件为单钉单剪连接件,2个连接板的材料均为30CrMnSi,厚度为6 mm。试验件的主要尺寸如图6所示。

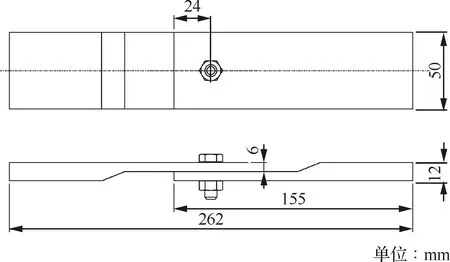
图6 传感器的剪切力测试装置Fig.6 Shear force test setup of force sensor

试验采用的试验机为Instron-8801,以力控的方法施加拉伸载荷,加载级差为1 kN,最大载荷为5 kN,试验机的加载误差小于1%。应变的数据采集设备为ST-24,每级载荷加载到后,数据采集设计测量一次。由于试验件的各零件间存在间隙,每次安装完成后进行预试,预试完成后,卸载,并检查设备,保证所有设备均处于正常工作状态,然后进行正式试验。试验前手动拧紧螺母。

传感器与连接板组成的试验件通过多次安装、多次拆卸,得到5种安装状态下的数据。单次测量得到的传感器载荷-应变曲线见图7。由图看出,各个应变片的载荷-应变曲线的线性均较好。5种安装状态的传感器载荷-剪切应变曲线见图8(剪切应变按式(9)计算),可看出,5次测量结果的线性良好。采用直线方程γ=λF拟合得到5次测量的柔度系数和线性相关系数见表2所示。由表2可见,传感器单次测量的载荷-剪切应变曲线的线性相关系数均大于0.99,表明载荷-剪切应变的线性相关度很高；5次测量的离散系数为0.67,表明传感器的测量结果重复性好。满足作为传感器的使用要求。

传感器在粘贴应变片处的横截面面积为As,承受的外载荷为剪切力F。根据材料力学理论,传感器在粘贴应变片处的平均剪切应力为F/As,又因为剪切应力可表示为Gγ,由此可得到剪切应变与剪切载荷之间的关系式(20)。

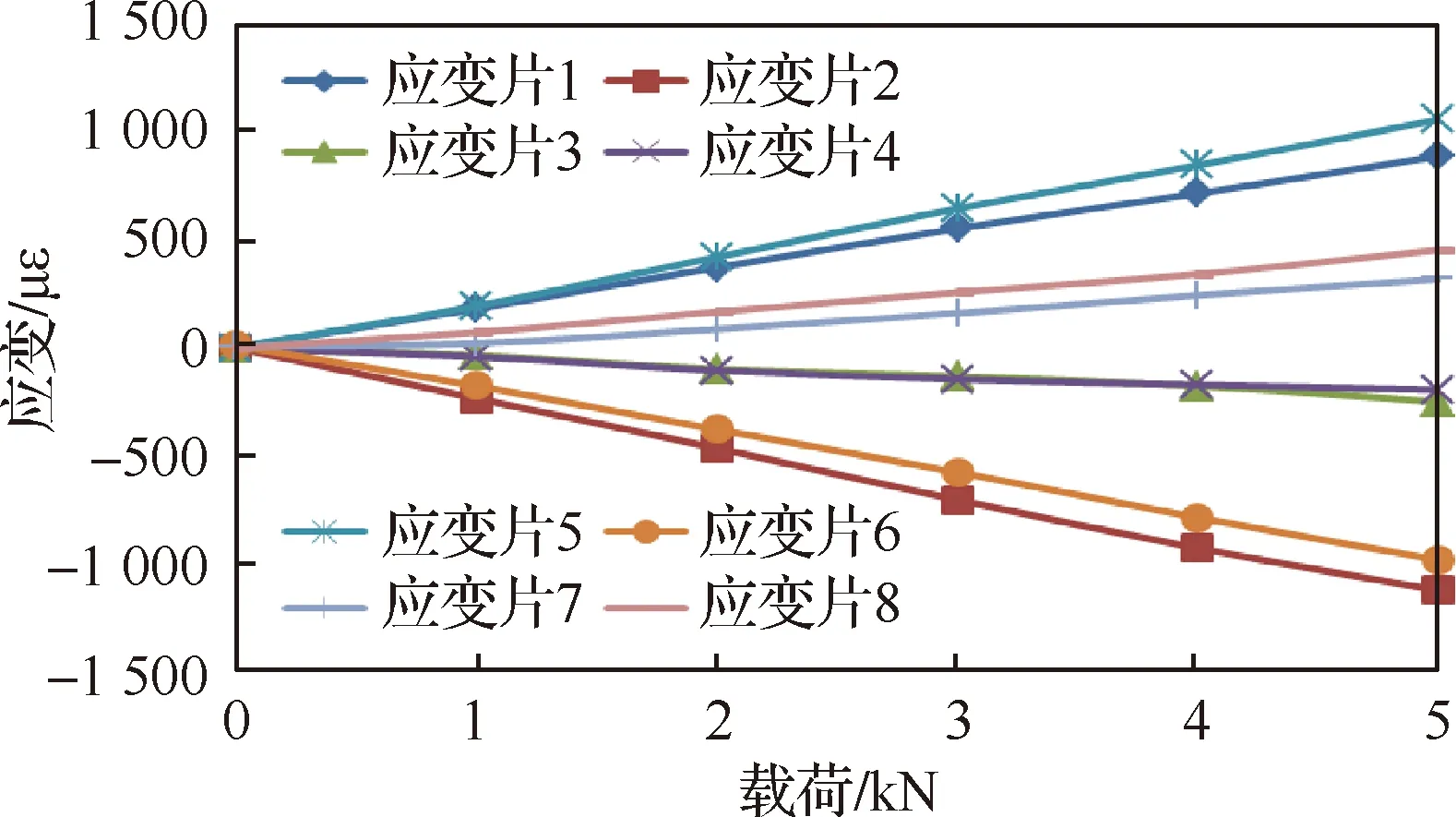
图7 剪切力测试中传感器的载荷-应变曲线Fig.7 Load-strain curves of force sensor in shear force test

图8 剪切测试中传感器的载荷-剪切应变曲线Fig.8 Load-shear strain curves of force sensor in shear force test

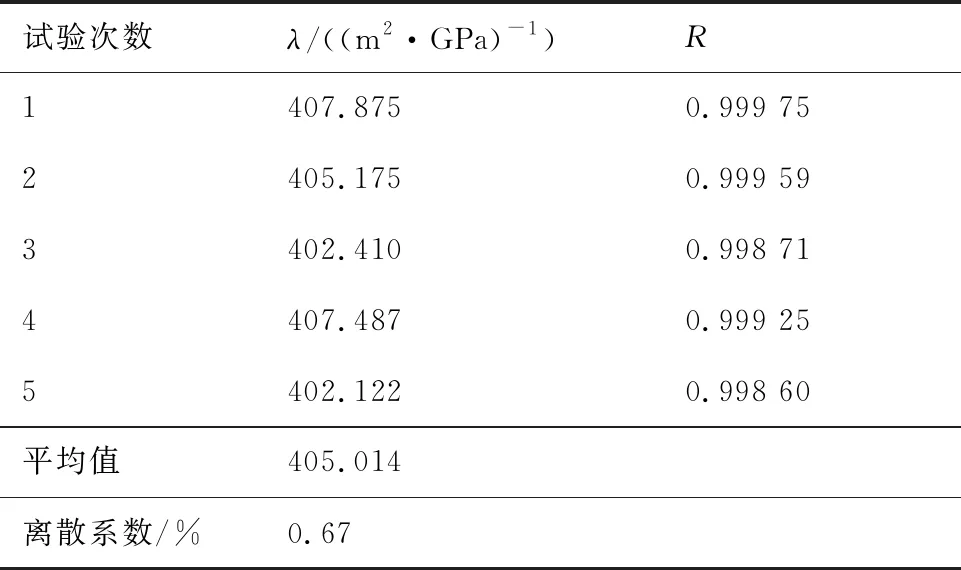
表2 传感器的剪切柔度系数和线性相关系数

(20)

式中：G′为传感器的剪切弹性模量,取值为75 GPa；面积As为33 mm2,应变γ为微应变,外载荷F的单位为kN,由此可计算常数λ的理论值约为403,与表2中测试的平均值很接近(误差为0.5%),验证了传感器剪切测试结果准确性和可靠性。

3.2.2 安装角的影响

为了研究传感器的安装角度与载荷方向的关系,对一系列的安装角进行测试。传感器的安装角即为应变片1、应变片2的粘贴面与载荷方向的夹角,见图9。传感器沿逆时针旋转为正,沿顺时针旋转为负。不同安装角传感器的载荷-剪切应变曲线见图10。由图可见,不同安装角测得剪切应变很接近,因此可认为安装角对传感器剪切力的测量无影响。

图9 传感器的安装角Fig.9 Installation angle of force sensor

图10 不同安装角传感器的载荷-剪切应变曲线Fig.10 Load-shear strain curves of force sensor of different installation angles

3.2.3 紧力矩的影响

为了研究不同的紧力矩对传感器剪切力测试的影响,对3种不同的紧力矩进行测试,3种紧力矩为：0 N·m(手拧紧)、4 N·m、8 N·m。

3种情况传感器的载荷-应变曲线见图7和图11。可看出,手拧紧情况载荷-应变整个曲线段的线性较好,另外两种情况出现明显非线性,曲线可看成由两段直线组成,第1段直线的斜率较小,第2段斜率较大。紧力矩越大,第1直线段越长,第2直线段的斜率越大。

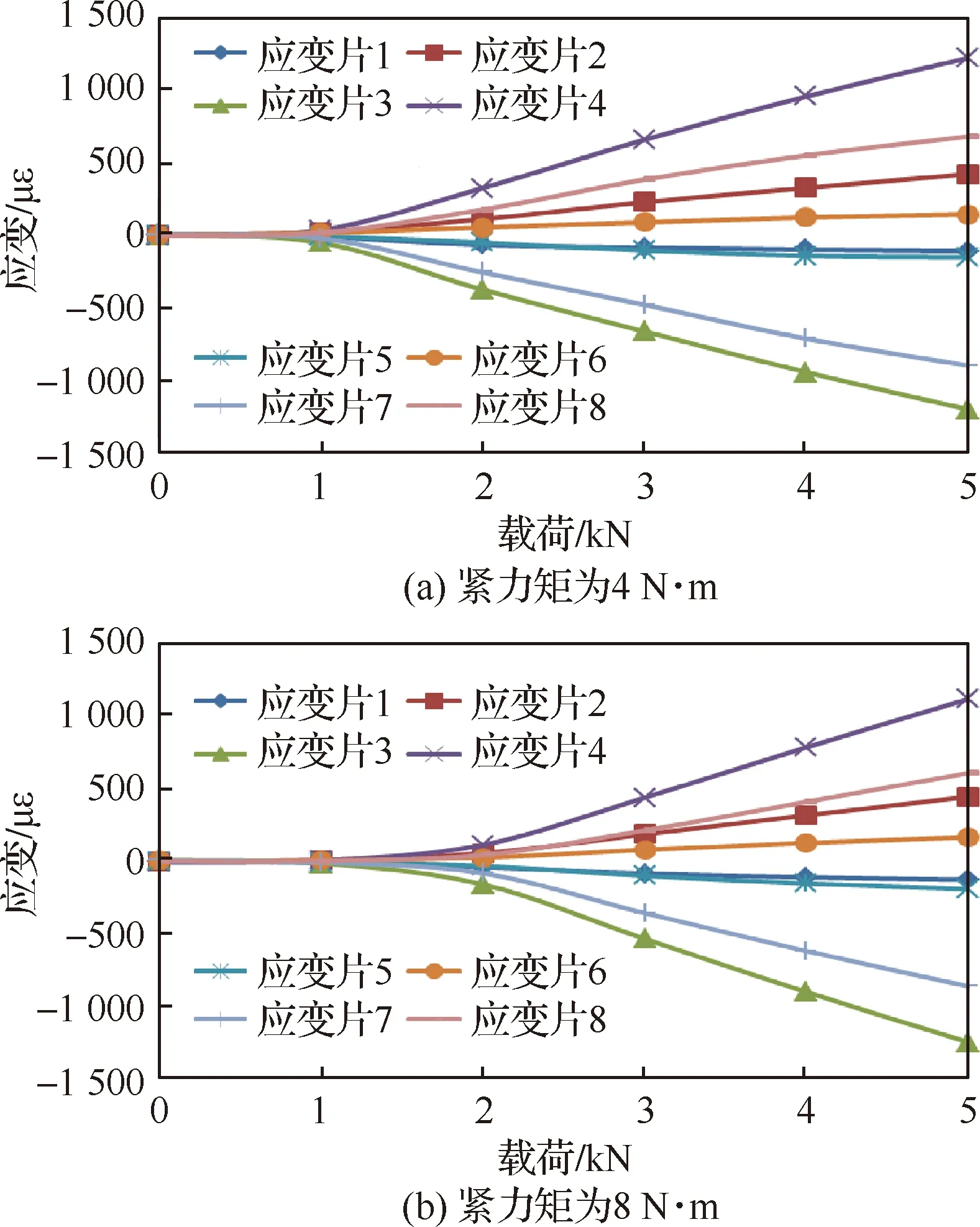
图11 剪切力测试中不同紧力矩传感器的载荷-应变曲线Fig.11 Load-strain curves of force sensor with different tightening torques in shear force test

3种情况的最大剪应变比较见表3。可看出,3种情况的最大剪切应变比较接近。主要原因是受摩擦力的影响,摩擦力包括传感器头与连接板的摩擦力、螺母与连接板的摩擦力、连接板之间的摩擦力。紧力矩越大,各零件间的摩擦力就越大,在开始阶段,试验件的外加载荷被摩擦力抵消,传感器的剪切力为0,载荷-应变曲线的斜率也为0。当外载逐级增大,摩擦力的影响减小,外载荷主要转化为传感器的剪切力。因此,随着外载荷的增大,紧力矩对传感器的剪切测试的影响逐渐减小。

由剪切测试得到的应变,根据式(17)可计算传感器的拉伸应变,进而由图8或表2可得到剪切试验中传感器的轴力。不同紧力矩情况下加载到5 kN时传感器轴力大小对比见表4。可看出,紧力矩越大,轴力越大；但扣除紧力矩最初产生的轴力,不同紧力矩情况下测试过程中增加的轴力(表4第3列数据)相当,即增加的轴力受紧力矩影响很小。

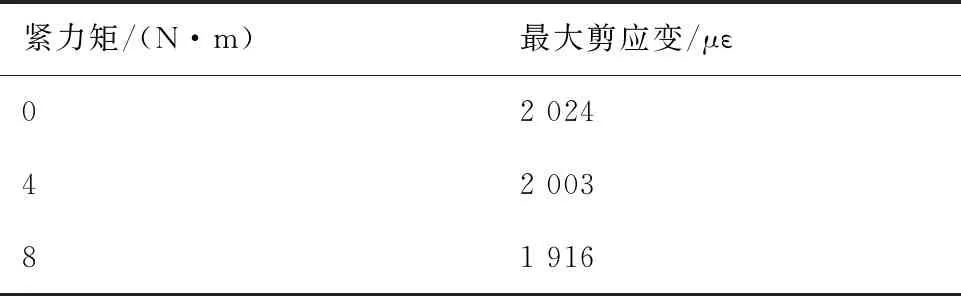
表3 剪切力测试中不同紧力矩情况下传感器的最大剪应变对比

表4 剪切力测试中不同紧力矩情况下加载5 kN时传感器的轴力对比

4 结 论

基于应变测量方法,提出一种连接结构中钉的轴力、剪切力测量传感器,并通过两种试验装置对传感器的轴力和剪切力进行测试试验。

1) 提出的传感器的载荷-应变关系曲线线性相关性高、多次测试重复性好,能满足工程使用要求。

2) 传感器能同时测量机械连接结构中钉的轴力和剪切力。

3) 传感器的安装角对轴力和剪切力的测试结果无影响。

4) 在剪切力的测试中增大紧力矩会使得传感器的载荷-应变曲线出现非线性,增大载荷后紧力矩的影响会逐渐减小。