直角切削6061-T6铝合金剪切区力学行为及微观结构演化预测

周滔,何林,2,*,田鹏飞,杜飞龙,3,吴锦行

1. 贵州大学 机械工程学院,贵阳 550025 2. 六盘水师范学院 矿业与土木工程学院,六盘水 553000 3. 贵州大学 现代制造技术教育部重点实验室,贵阳 550025

机械加工属于典型的基于热力耦合的塑性变形过程,并伴随材料的微观结构演变。过去几十年发展起来的基于物理的解析方法为理解机械加工过程奠定了坚实的基础,但是早期的解析性模型(如Merchant[1]、Hill[2]和Lee[3])在模拟切削过程中的切屑变形涉及的力学行为时,大多没有考虑金属材料的微观结构性能,而切削过程中金属材料的力学行为与微观结构紧密相连。近年来,大量包含微观结构的材料模型[4-5]被成功开发和应用,甚至扩展到高应变、应变率和高温变形过程[6-7],所以当前研究切削过程中微观结构演化并将其嵌入到预测加工理论模型已经成为可行。

为了将微观变形与宏观力学行为联系起来,很多研究人员做了相关的建模工作。如Pan等[5]提出在Johnson-Cook(JC)方程中考虑晶粒长大的影响,并将其代入Oxley模型中迭代计算切削力,模型提高了预测精度。金属材料在高温塑性变形时,变形机制主要表现为扩散,当切削温度相对于熔点较低时,变形机制主要有位错和孪生。为了更好地描述切削加工这类冷加工大变形条件下的材料行为,有很多基于金属位错机制的材料模型(Dislocation Density-based Material model, DDM)被开发利用,Bammann等[8]考虑应变率、温度和损伤建立了一个基于位错密度的材料模型。Guo等[9]预测切屑形貌时,发现与JC模型相比,Bammann-Chiesa-Johnson (BCJ)模型更为准确。Follansbee和Kocks[10]建立了一个基于热无关应力和热应力的粘塑性模型,且考虑了初始晶粒尺寸的影响。Ding和Shin[11]基于位错的增殖和湮灭过程有效地预测了切削AISI 52100 steel的切削力、切削温度和切屑厚度。Liu等[4]验证了考虑位错拖拽的统一材料模型在大范围内的切削力预测准确性。这些基于物理的材料模型在预测性能上的改进使得它们比非物理动机的唯象学模型更有吸引力。

建立微观结构演化过程与切削条件之间的关系是金属加工过程建模的另一个挑战。6061-T6铝合金具有中等强度、良好的抗腐蚀性、可焊接性,氧化效果较好,广泛应用于要求有一定强度和抗腐蚀性高的工业结构件[12],例如航天固定装置、电器固定装置及自动化机械零件等。Ding等[7]采用Estrin等[13]开发的基于位错密度的材料模型模拟了6061-T6铝合金切屑在直角切削过程中的晶粒细化。Arisoy和Özel[14]结合平均晶粒的计算方法提出了车削Ti-6Al-4V时的晶粒尺寸演化有限元模型,结果表明,再结晶晶粒对材料在主剪切区的力学行为有显著影响,从而导致了切屑的分段,这甚至可以用于揭示钛合金锯齿状切屑[15]的形成机理。Jafarian等[16]使用再结晶机制模拟了直角切削Inconel718的微观结构变化,其中考虑晶粒尺寸的流动应力模型正确反映了材料力学行为。以上研究中,在考虑微观结构演化对材料的力学行为影响时,大多是基于有限元法(Finite Element Method, FEM)实现。相对于FEM的微观结构演化预测,解析模型为加工过程建模提供了一种简便的方法,具有较高的计算效率,可以显式地计算加工过程中材料的热力耦合响应。

综上所述,本研究的目的是结合金属材料微观结构中位错变形机制和预测加工理论,建立一种能描述主剪切区(Primary Shear Zone, PSZ)力学行为和模拟微观结构演化过程特征的解析模型。首先将位错密度材料模型与等分模型和非等分模型结合,构建了剪切区应力场和温度场分布的计算流程,提出了切屑微观结构(位错密度和晶粒尺寸)演化解析模型,然后使用透射电子显微镜结合选区电子衍射对直角切削6061-T6铝合金的切屑塑性变形状态进行观测,对等分模型和非等分模型的切削力预测结果进行了验证,通过混合等分模型和非等分模型给出的应变场和温度场,预测了剪切区微观结构演化过程,实验结果证明了所建立模型的可行性。

1 位错密度材料模型

切削剪切区的大塑形应变累积导致的位错运动会使切屑材料发生晶粒细化,如图1 所示,本文在描述剪切区力学行为时,为了模拟切屑形成过程中的晶粒细化过程,采用基于位错密度的材料模型。

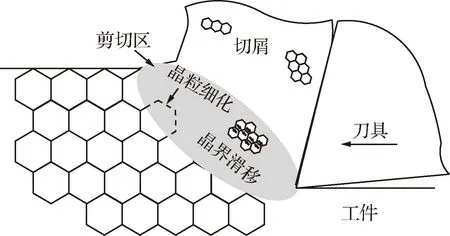
图1 剪切区晶粒细化Fig.1 Grain refinement of shear zone

为了反映切削过程中剪切区力学行为,建立切屑内位错密度和晶粒尺寸的演化模型,引入由Estrin等[13]建立的位错密度材料模型,该模型由胞壁和胞内两部分组成,在塑性变形过程中形成位错胞结构,分为胞内位错ρc和胞壁位错ρw,其中胞壁位错又由统计位错ρws和几何必需位错ρwg组成,每一种位错的演化遵循不同的计算方法,ρc、ρws和ρwg的微分方程为

(1)

(2)

(3)

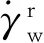
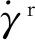
(4)

(5)

通过位错胞壁体积分数、位错密度和晶粒尺寸之间的关系,可以得到表达式分别为

(6)

ρtot=f(ρws+ρwg)+(1-f)ρc

(7)

(8)

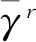
在建立的解析模型中,通过考虑位错密度来计算金属材料的流动应力,以此确定力学性能,通过Taylor因子M进一步定义了流动应力σ和分解剪应力τr的关系

τr=σ/M

(9)

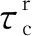
(10)

(11)

式中：G为剪切模量；1/m为应变速率敏感参数；a为常数在0.25到0.5之间。“混合”材料的整体性能由τr来定义,其根据式(12)的两“相”混合规则得到

(12)

其中,n和m与温度有关,m=A/T,n=B/T,A和B为常数,T为温度。

2 基于热力耦合的切削力预测

在预测切削力时,解析模型和有限元数值方法得到了广泛的应用,虽然有限元具有高精度和多功能等优点,但是需要花费更多的时间来模拟。Oxley预测加工理论基于对材料变形的实验观察,在平面应变和稳态切削条件的假设下可以实现计算效率高且精确的预测,同时建立起直角切削输入变量(材料特性、刀具几何形状和切削条件)与输出变量(变形区的温度、切屑几何形状、切削力等)之间的理论关系。

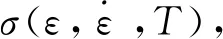
通过图2所示剪切区和刀具-切屑接触区的平衡关系可以求解出各切削力分量和切屑厚度t2,如式(13)～式(18)所示:

Fc=FRcos(λ-α)

(13)

Ft=FRsin(λ-α)

(14)

Ff=FRsinλ

(15)

Fn=FRcosλ

(16)

(17)

t2=t1cos(φ-α)/sinφ

(18)

式中：φ为剪切角；α为刀具前角；λ为摩擦角；t1为未变形切屑厚度；w为切削宽度；Fc和Ft为切屑形成力在切削方向和垂直于切削方向上的分量；Ff为刀具-切屑界面的摩擦力；Fs为剪切面上的切削力；FN和Fn分别为剪切面和刀具-切屑界面的法向力；FR为Ff和Fn的合力；Fc和Ft的合力为-FR；θ为FR与AB的夹角；KAB表示剪切面平均流动应力。已知剪切面上的剪切应力和刀具-切屑界面的摩擦角,在给定刀具几何形状和切削条件下,可以预测直角切削过程中的切削力。

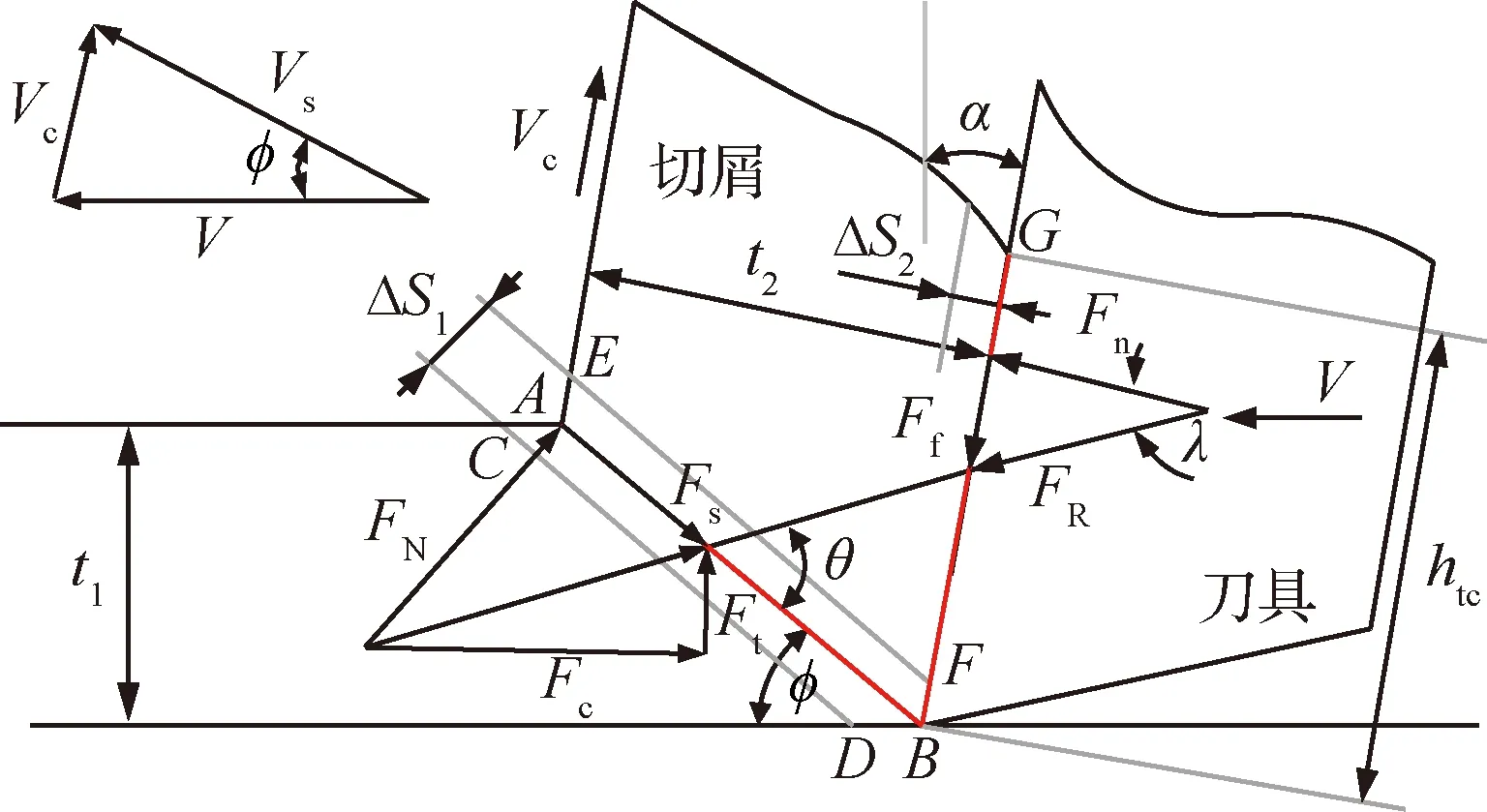
图2 直角切削几何关系Fig.2 Geometric relations of orthogonal cutting

假设从A到B的任意质点在切削方向x和垂直于切削方向y上的速度和位移增量分别为

(19)

(20)

式中：V为切削速度；ΔS1为第一变形区厚度。

Oxley模型[18]中剪切区材料流动速度分量和平均剪应变速率之间的关系为

(21)

将式(19)和式(20) 代入式(21),可得平均剪应变速率表达式

(22)

剪切角φ确定后,根据von Mises应力屈服准则,剪切区的AB处等效应变和等效应变率为

(23)

(24)

假设所有的变形都发生在剪切平面上,在剪切平面上工件材料变成了切屑,初始切削速度为V的工件材料,随着切削速度的增加,会突然向切屑转变,速度的这种突然变化沿剪切面产生了速度不连续,即所谓的剪切速度,通过图2的速度矢量关系图可以计算切屑材料流动速度Vc和剪切面的材料流动速度Vs:

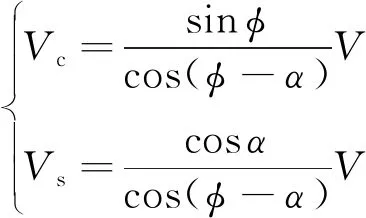
(25)

切削时的摩擦角计算公式为λ=θ+α-φ,可以得到摩擦系数μ=tanλ,根据Oxely理论,图2中的剪切角φ和夹角θ满足以下关系：

(26)

修正的应变率常数C0考虑了材料应变的影响[19],其表达式为

(27)

式中：COxley为第一变形区剪切带长宽比；AJC、BJC和nJC为JC本构参数。

由于剪切应力与温度有关,因此需要迭代计算AB的温度,直到达到稳态。根据Boothroyd温度模型[20],平均温度的表达式为

(28)

式中：Tr为室温,η为总剪切能转换为焓的比例,分析中取0.9[20]；ρ为工件材料的密度；Cw为工件材料的比热。其中热量分配系数β计算[21]如下

β=

(29)

(30)

式中：Kw为热传导系数；R0为无量纲热系数。

图2中靠近刀尖位置处的B点的正应力σ′N可结合剪切面的平均流动应力得到

(31)

分析第二变形区时,通常假设刀具-切屑界面的塑性变形区域的厚度为常数：ΔS2=δt2,δ为第二变形区厚度与切屑厚度之比。因此,得到刀具-切屑界面的等效应变和等效应变率为

(32)

(33)

式中：刀具-切屑接触长度htc根据剪切面的力矩平衡公式求出

(34)

假设刀具-切屑界面应力均匀分布,得到刀具-切屑界面应力τint和B点的应力σN表达式为

(35)

刀具-切屑界面的平均温度Tint表示为

Tint=Tr+ΔTsz+ψΔTM

(36)

(37)

(38)

式中：Ψ为修正系数,取为0.6[20]；ΔTM为切屑中的最大温升；ΔTc为切屑中的平均温升；ΔTsz为第一变形区温升。

基于热力耦合的切削力预测模型中,求解剪切区温度时,先在给定的初始温度下,确定剪切区的流动应力,然后根据流动应力使用式(28)更新剪切面的温度,并替换为初始启动温度,开始新的计算,这个过程不断重复,直到起始温度和计算温度之间的差值小于给定值0.1 ℃,根据三个迭代条件[21](刀具-切屑界面处的应力平衡、刀尖处的应力平衡和切削力Fc最小原则)确定剪切角φ和变形区应变率系数COxley和δ,输出切削力。

由于切削过程中的变形具有典型的高应变、高应变速率和高温的特点,在之前修正的Oxley模型中,剪切区和切屑中相应的平均流动应力采用Johnson-Cook本构方程表示：

(39)

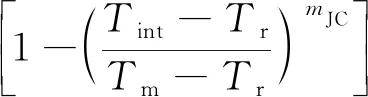
(40)

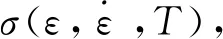
在计算切屑形成力时,假设刀尖是完全锋利的,而实际加工过程中刀尖通常设计为具有一定半径的圆弧以提高刀具寿命,此时刀尖与已加工表面接触产生犁削力。如图3所示,采用Waldorf等[22]提出的滑移线场模型用来预测由于刀尖钝圆作用产生的犁削力。

如图3所示,扇形区的角ηplow、θfan和γplow由几何和摩擦关系得

BC=Rfan/sinηplow

(41)

ηplow=0.5arccosμplow

(42)

(43)

(44)

式中：μplow为摩擦因子,取为0.99[23]；ρplow指刀刃半径re导致未加工凸起部分与水平面的夹角,设置为10°[23]；扇形区扇形半径Rfan计算公式为

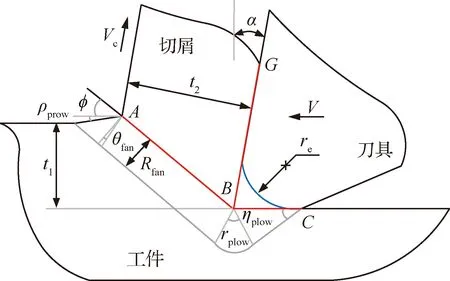
图3 犁削滑移线模型Fig.3 Model of slip-line field for plowing

(45)

已知剪切角和剪切面的流动应力,用式(46)和式(47)可求得犁削力。犁削力被分解为沿切削方向的犁削力Pc和垂直于切削方向的犁削力Pt：

Pc=KABwBC[cos(2ηplow)cos(φ-γplow+ηplow)+

(1+2θfan+2γplow+sin (2ηplow))·

sin(φ-γplow+ηplow)]

(46)

Pt=KABwBC[(1+2θfan+2γplow+sin(2ηplow))·

cos(φ-γplow+ηplow)-cos(2ηplow)·

cos(φ-γplow+ηplow)]

(47)

总切削力由切屑形成力和犁削力叠加而成。在切削方向上的总切削力Fx和垂直于切削方向的力Fy表示为

(48)

3 非等分剪切区建模

在Oxley的预测加工理论中,解决了材料塑性变形过程中加工硬化和热软化的影响,然而,应变、应变速率和温度都是根据平均值计算的。虽然这些参数的分布对描述介质连续流动是必不可少的,但Oxley模型没有考虑到这些参数的分布。该部分以前一节的预测为基础,对剪切区应力场和温度场分布进行了预测,如图4所示,在非等分剪切区(Unequal division shear zone, UDS)的框架下,建立了一种基于唯象的非线性剪切应变率分布模型。

研究人员从落刀实验分析中发现,剪切带被AB分成两个不等的区域,其中下区域(CD到AB)比上区域(AB到EF)宽。Astakhov等[24]得出,在较宽的下区域和较窄的上区域,剪切应变速率随速度的演化呈现不同的变化趋势。

根据Pang[21]的研究,以剪切区质点位置ys

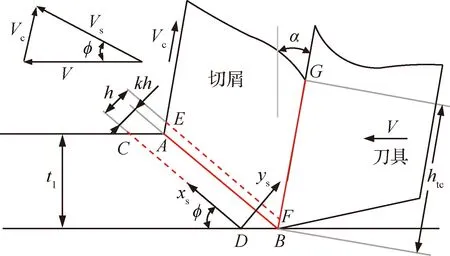
图4 非等分剪切区模型Fig.4 Unequal division shear-zone model

和剪切区厚度h表示的四阶多项式曲线可以描述剪切应变率在主剪切带的分布

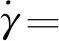
(49)

其中需要确定的系数为D1、E1、F1、d1、e1、f1[21]。

由图4分析可知,若k定义为变形区下半部分占总厚度的比例,则主剪切区速度场和剪切应变率场的边界条件为

1) 初始剪切区被AB(ys=kh)不均匀地分为宽区和窄区。

2) 塑性变形量取决于垂直主剪切带的距离ys。

3) 在主剪切区的AB处切向速度为零(Vxs|ys=kh=0)。

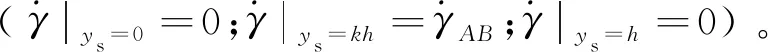
5) 由于材料颗粒以恒定的速度向主剪切区移动,在到达下边界CD之前,速度和相应的剪切应变率的变化率为零,同样,通过上边界EF后,颗粒的应变率再次下降到零。假设应变率分布由光滑的可微曲线来表示,则在CD和EF边界,需要有一极薄的缓冲带,剪切应变率相对于ys的梯度为零。此外,假定曲线的可微性导致剪切应变率相对于ys的梯度在AB上也为零,剪切应变率达到最大值,即

(50)

通过以上分析,可以得到剪切区剪切应变率和速度分布如式(51)和式(52)所示:

(51)

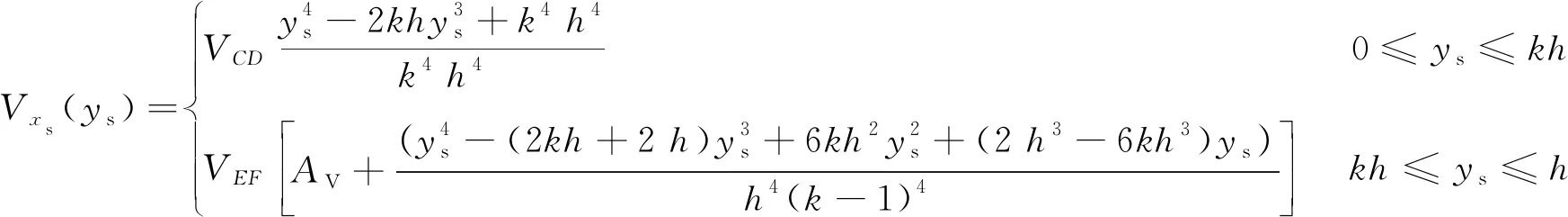
(52)

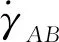
(53)

(54)

在非等分模型中,剪切应变的分布根据速度与剪切角的关系进行计算

(55)

在以上解析建模中,需要使用Oxley模型的输出变量：剪切角φ、第一变形区剪切带长宽比COxley和长度LAB、剪切面的平均温度TAB。剪切角用于坐标系的角度计算和定位,COxley和LAB用于计算非等分剪切区厚度h,平均温度用于迭代计算温度和流动应力在剪切区厚度方向的特征分布。

导致主剪切区温度升高的热量可分为两部分,一个是热传导,另一个是热扩散。导热反映了物体之间的传热,代表了导热能力。然而,热扩散在不同工况下表现不一致,我们假设热扩散的比例是R。主剪切区中的热量来源于加工过程中的塑性变形,因此,在主剪切区中任何垂直于ys轴方向的微平面上,单位时间内产生的热量可以确定为

(56)

式中：τ为剪切应力。

在剪切区任何垂直于ys轴的微平面上,热扩散对温升的影响为

(57)

根据Zhou等[25]的研究,因传质传热所引起的温度分布可以根据边界条件结合式(57)进行转换,所以沿ys轴方向温度分布的分段函数为

T=

(58)

4 实验与分析

4.1 实验过程

在上述分析的基础上,为了验证本文模型的可行性,开展了直角切削实验,观测了6061-T6铝合金的切削力及切屑微观结构,6061-T6铝合金的模型参数和物理性能参考文献[7]。

直角切削方案示意图如图6(a)所示,棒材尺寸为∅200 mm×80 mm,首先对棒材进行切槽加工,槽宽和槽深均为5 mm,得到12组宽约3 mm的环形凸起表面,然后对每一组外圆表面进行直角车削,切槽和切外圆均在数控车床型号为C6136HK的车床上进行。刀具宽度为5 mm的硬质合金切槽刀,使用Alicona刀具形貌观测仪器测量了切槽刀具的刀尖钝圆半径,如图6(b)和6(c)所示,为刀具A和B的刃口形貌和结构示意图,其中刃口形貌的云图表示刀具质点距离基准点的高度。

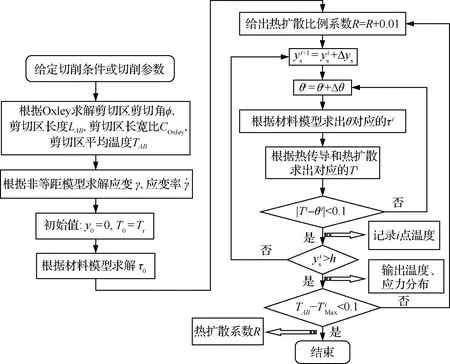
图5 PSZ的R和温度分布的求解流程图Fig.5 Flow chart of solving process of R and temperature distribution in PSZ

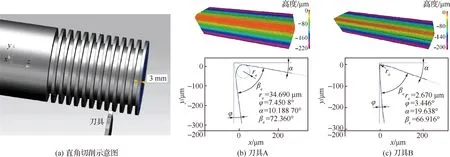
图6 直角车削和刀尖结构示意图Fig.6 Schematic diagram of orthogonal turning and edge structure

如图7(a)所示,采用KISTLER压电测力计9257B安装在机床刀架上,用于测量车削过程中三个方向的切削力,每组实验重复三次,计算其平均值。为了验证模型并分析切削参数对切削力的影响规律,设计了12组实验,实验设置如表1所示。第8组实验观测的切削力如图8所示,其中图8(a)为切削力的原始数据,图8(b)为滤波后对应的数据,可以看出测量的切削力数据较为平稳,相对于切向力Fx和径向力Fy,轴向力Fz近似为0,所以忽视不计,可以将切削过程近似为直角切削,用来验证切削力模型,我们分别观测了两种刀具在不同切削速度和切削厚度下的切削力数据。

材料在高温塑性变形时,扩散机理占重要作用,而切削大多数金属材料时,切削温度相对于熔点较低,所以变形机制主要有位错滑移和孪生变形。为了分析6061-T6铝合金切屑变形中是否有孪生,如图9所示,对第3组实验的切屑进行离子减薄,使用透射电子显微镜(Transmission Elec-tron Microscopy, TEM)观测塑性变形状态,并对其进行选区电子衍射(Selected area electron diffraction, SAED)。根据Atmani等[26]和Wu等[6]的研究显示,当金属材料经过变形区形成切屑后,从自由表面往刀-屑接触面方向上的较宽切屑厚度范围内的微观组织具有一定的均匀分布特性,切屑在较宽的面积内的位错密度和晶粒尺寸的演化主要发生在剪切区内,所以采集的切屑TEM是切屑自由表面到刀-屑接触面的中间区域。

图7 加工实验Fig.7 Machining experiment

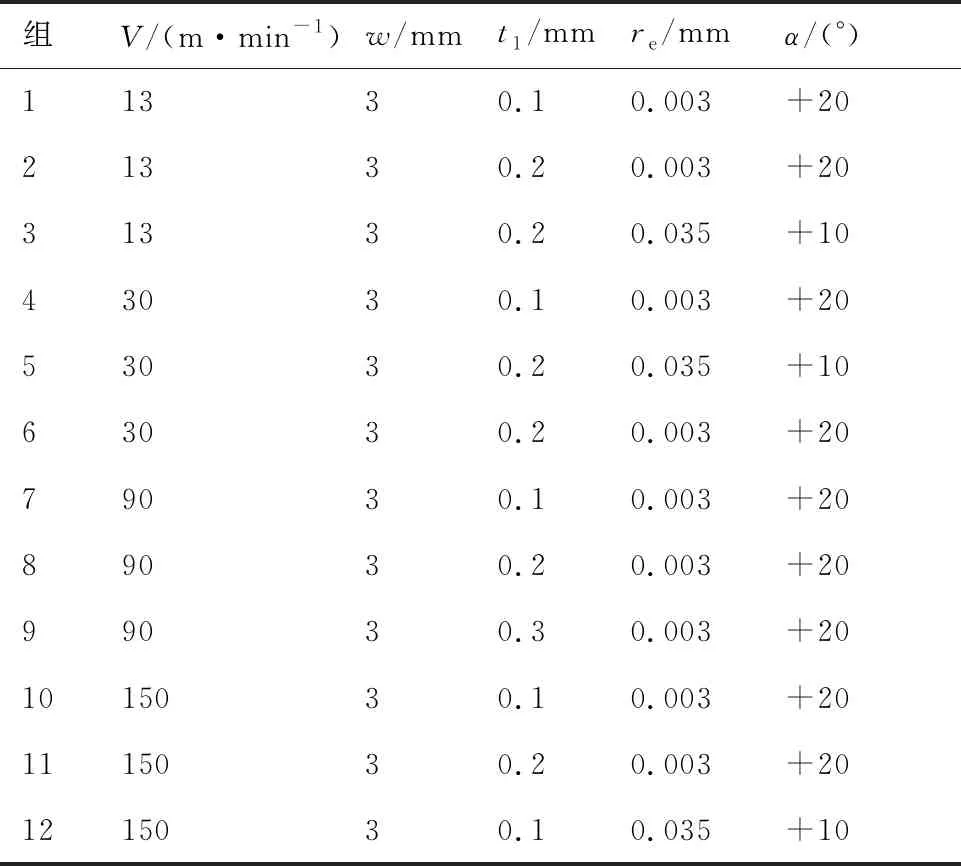
表1 直角车削参数Table 1 Parameters of orthogonal turning

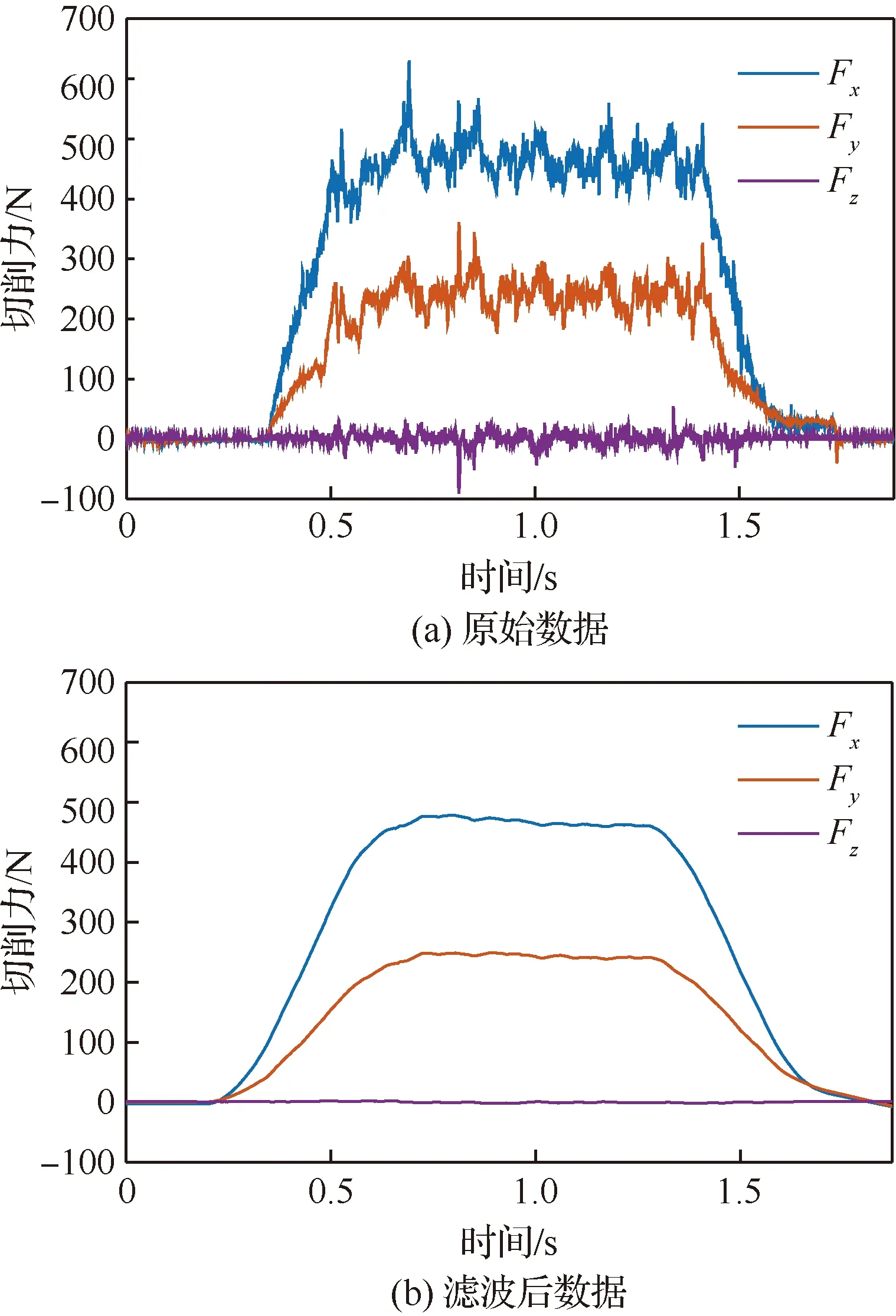
图8 切削力数据(V=90 m/min, t1=0.2 mm)Fig.8 Data of cutting force (V=90 m/min, t1=0.2 mm)

如图9(a)和图9(b)所示,切屑内呈现典型的塑性变形状态,位错密度较高,部分区域为位错胞构成的片层结构,并包含了大量位错塞积形成的位错墙。图9(c)和图9(d)为A1和A2区域的SAED,通过标定分析,并未发现孪晶的存在,因为面心立方结构的6061-T6铝合金表现为高层错能材料,拥有较高的堆垛层错能,不会轻易出现孪生变形,位错运动是其主要的塑性变形方式,这也证实了基于位错密度的材料模型适用于反映材料冷加工变形的微观结构变化与宏观的力学行为之间的联系。切削过程中,材料流经第一变形区时,剪切应变逐渐增大,由于纯剪切变形的作用,材料中的粗大晶粒发生剪切和破碎,使原来粗大的晶粒沿剪切变形方向被拉长成条带状,同时晶体中的增殖源处位错数量自发增多,Frank-Read位错源是位错增殖的主要机制[27]。

4.2 预测结果分析

4.2.1 等分模型预测结果分析

观测和预测的切削力如图10所示。从整体上可以明显看出,结合JC模型预测的切削力和结合DDM预测的切削力均较好地反映了切削力随参数组合的变化。图10 (a)为预测的切向力,12组切向力预测值的平均百分比误差分别为6.2%和4.9%。图10(b)为预测的径向力,JC模型和DDM模型预测值的平均百分比误差分别为11.5%和7.8%。

在改进的Oxley模型的迭代求解过程中,中间输出变量较为复杂,系统性的求解过程决定了最终的切削力值。考虑金属材料冷加工中的微观结构的变形行为时,主要以位错运动为塑性变形机制引入到模型的求解过程。尽管之前唯象模型是模拟金属成形过程中涉及高应变、应变速率和温度效应的最常用模型,但是,本文结合位错密度模型和Oxley预测加工理论得到的切削力相对于结合唯象的JC模型更加准确。Liu[4]指出在材料模型中包含大量相关的底层微尺度变形机制时,将在校准范围之外产生更准确的预测。当应变和温度分别在0.1～3和25～250 ℃之间,应变率分别取100 1/s和5 000 1/s时,JC模型和DDM模型的应力-应变曲线如图11所示。可以从图中看出两种材料模型的应力-应变关系较接近。这说明更多涉及金属位错机制的物理模型可以更好地描述在类似于机械加工加载条件下的工作材料力学行为。

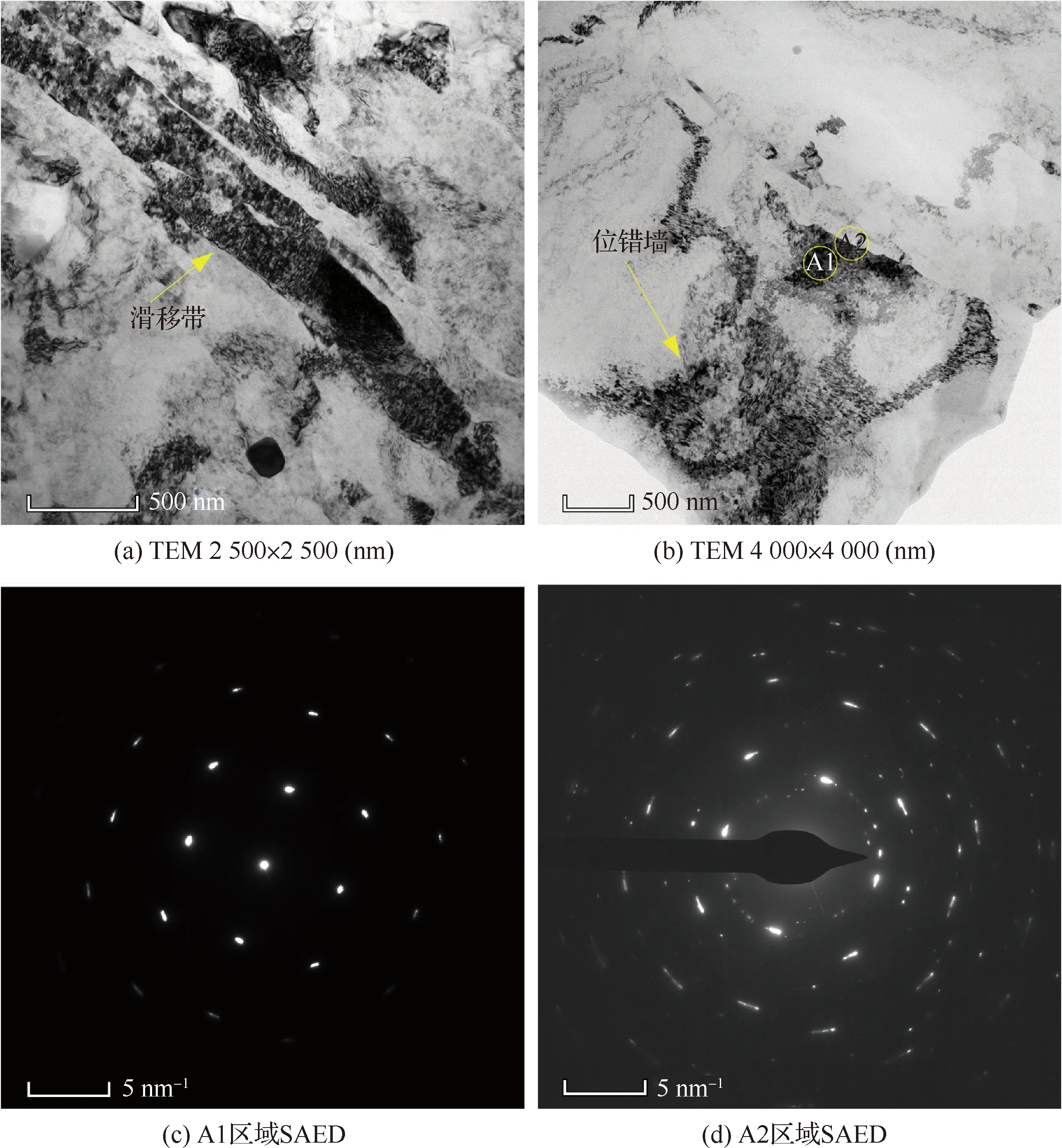
图9 切屑的TEM明像场和A1、A2区域的SAEDFig.9 TEM bright field image of chip and SAED in regions A1 and A2

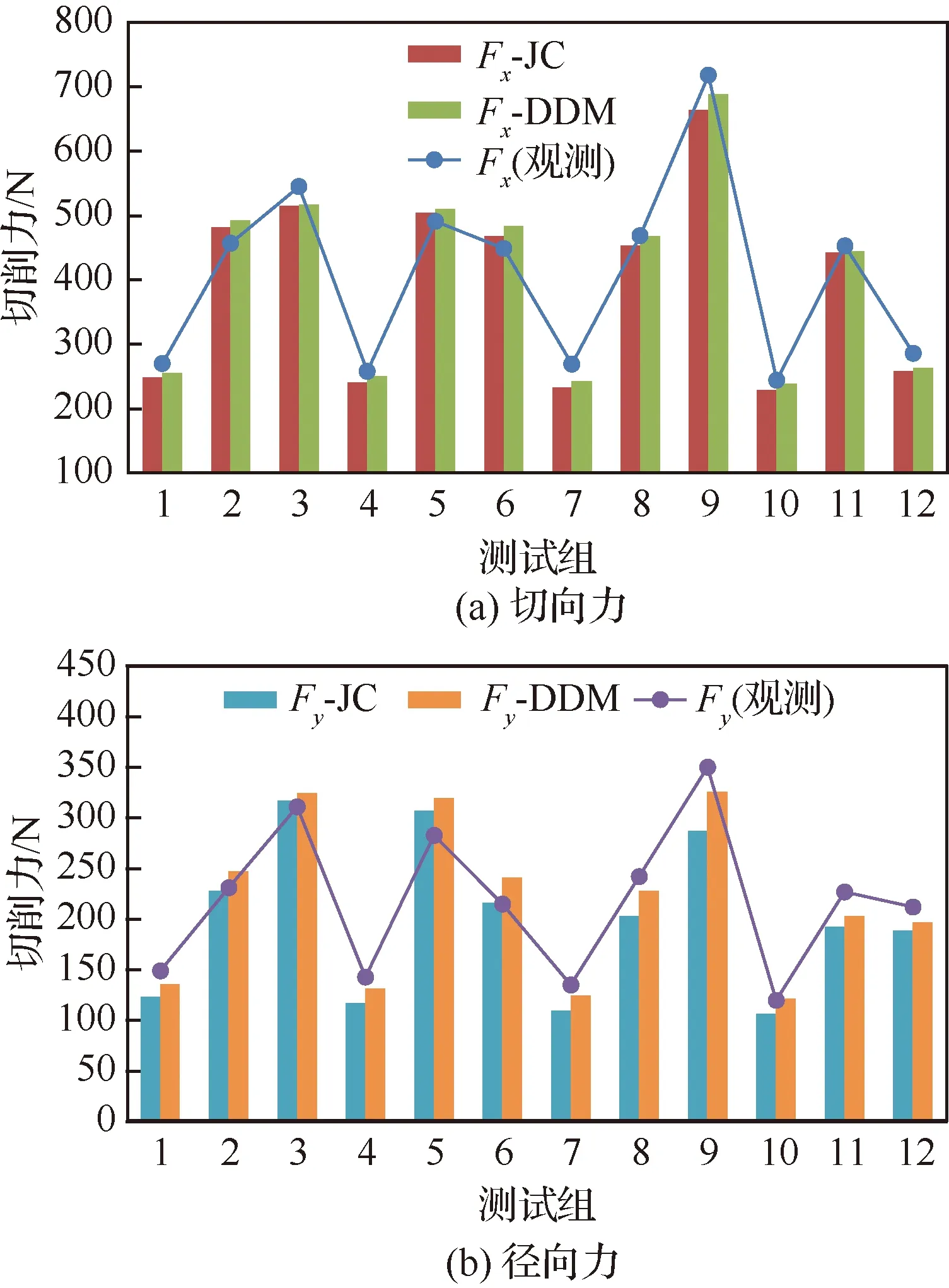
图10 切削力的实验值与预测值Fig.10 Experimental and predictive values of cutting forces

在改进的Oxley 模型中,工件材料特性和切削参数为输入变量时,输出的结果包括φ、COxley、LAB、δ、TAB、Tint、εAB和εint等,如表2所示,为模型求解得到的6组不同切削深度(第7、8和9组)和切削速度(第1、4、7和10组)下的过程变量。从表中可以看出,剪切角随切削速度和切削深度的增大而增大,同时刀-屑接触区的平均温度高于剪切区平均温度,刀-屑接触区的应变大于剪切区应变,这是因为刀-屑接触区受到强烈的摩擦挤压作用导致[28-29]。

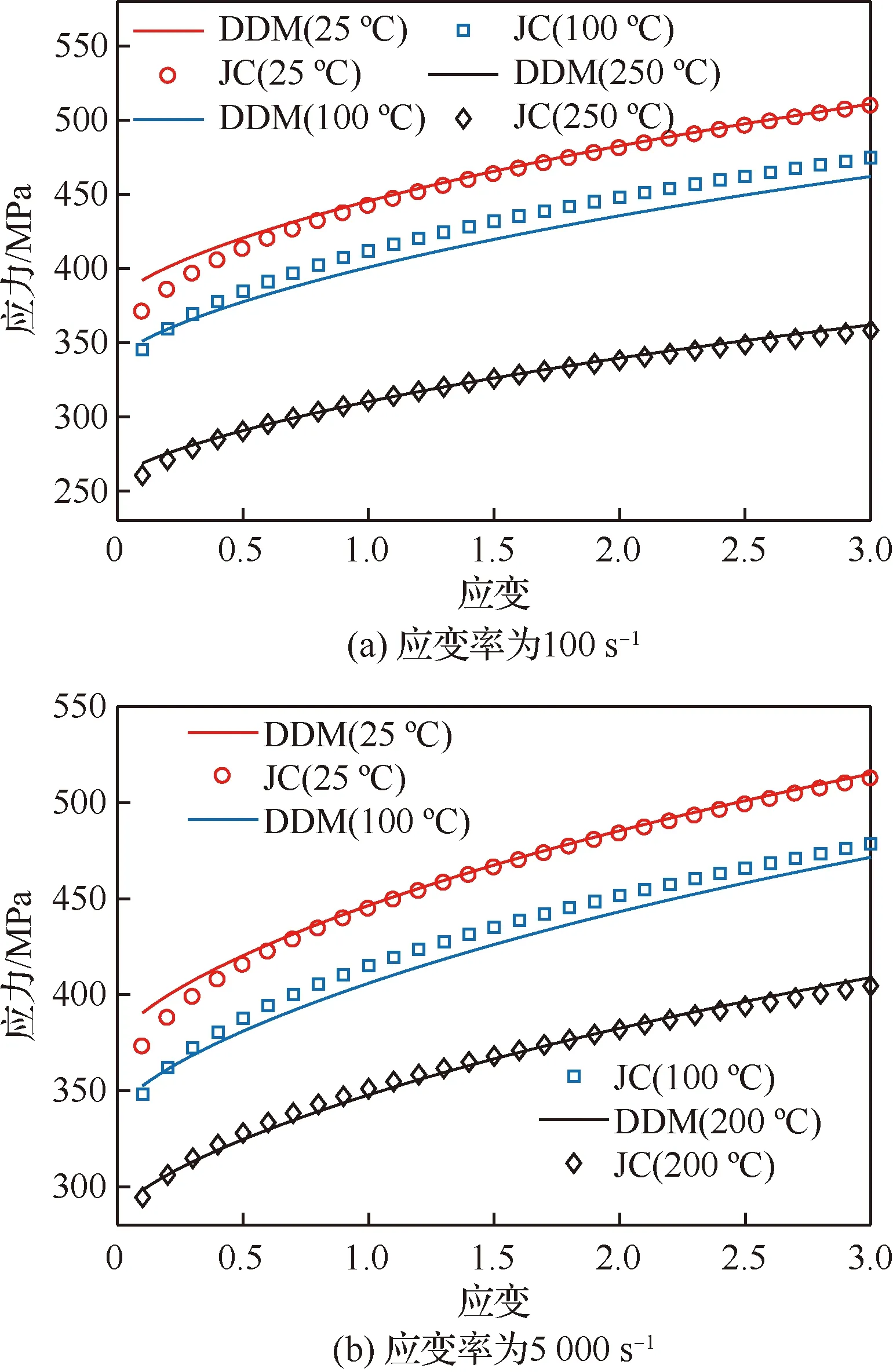
图11 6061-T6铝合金应力-应变曲线Fig.11 Stress-strain curves for 6061-T6 aluminum alloy

从表2中Oxley的计算结果可知,当切削深度增大,剪切区长度变长,然而剪切区和刀具-切屑摩擦区的温度升高并不显著。虽然剪切角增大和温度升高可能会导致切削力降低,但是由于增大切削深度导致材料去除率增大,直接影响到切削变形和刀具和切屑摩擦的增大[30],较长的剪切带导致参与位错滑移的材料增多,消耗的变形能将会更多,所以增加了能量的消耗导致切削力的增大。当切削速度增大,剪切角增大、变形区温度升高、剪切区和摩擦区应变降低,剪切区和摩擦区温度升高的趋势比切削深度引起的趋势更为明显,同时材料去除体积并未发生改变,由于应变降低引起剪切区位错增殖数量减少,位错密度降低[7],剪切区温度升高导致位错的湮灭作用增加,合金中位错的运动能力增加,动态软化加剧,从而降低了剪切区流动应力[31],所以切削速度增大导致切削力降低是多种过程变量共同作用的结果。

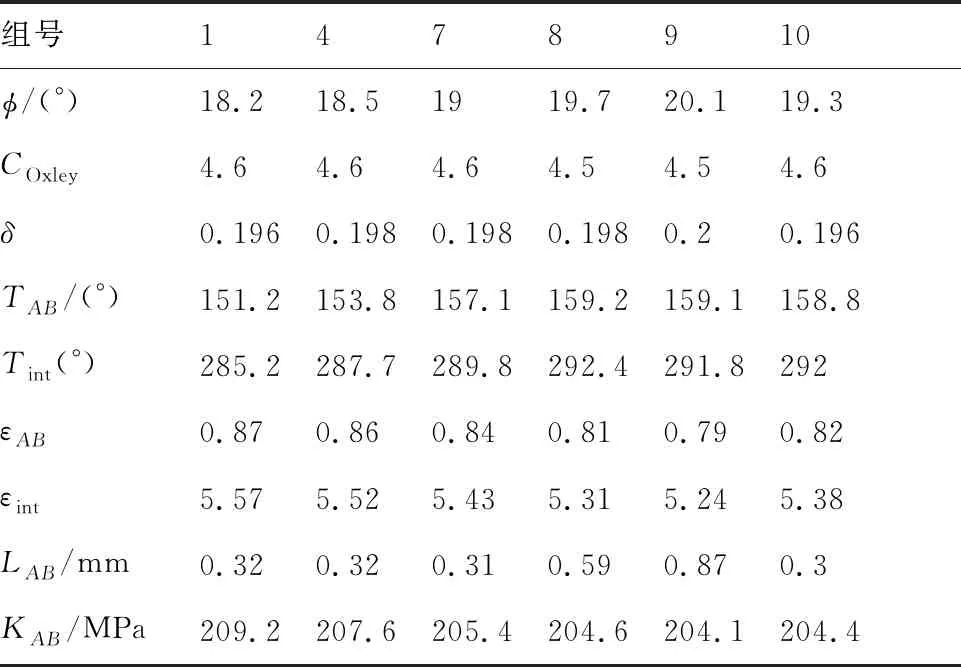
表2 改进Oxley模型的计算结果Table 2 Results of improved Oxley model

4.2.2 非等分模型预测结果分析

求解得到的3组切削速度(第4、第7和第10组实验)下的温度和剪切应力分布如图12所示,从剪切带入口到剪切带出口位置,温度逐渐增大然后趋于稳定,增大切削速度,剪切区温度升高。应力先逐渐增大后缓慢降低,过剪切区后急剧降低。

当材料质点经过剪切区低温阶段时,切削速度越大,剪切应力越大,这是因为剪切应变速率随着切削速度的增大而增大,动态力学行为关系表明,应变速率越大,位错增殖的数目增多,位错运动的速度加快,位错间的相互交割几率增大,以致变形时的临界切应力大幅提高。然而,当质点到达高温区域,由于受到热软化的影响,位错的湮灭作用增加,合金中位错运动能力增加,软化效应加剧,导致切削速度大的流动应力反而低一些。除此之外,从图12还可以看出较低的切削速度下,剪切区厚度h相对较厚,工件材料受到更多的时间和空间范围内外力的作用,所以切削速度降低会导致切屑内应力总体上增大。

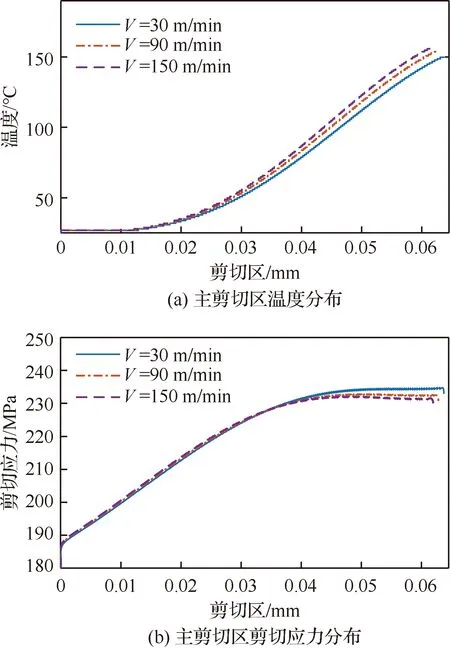
图12 主剪切带温度和剪切应力分布Fig.12 Distribution of temperature and shear stress in shear zone

根据非等分剪切区模型计算的剪切应力值,得到切削力预测值如图13所示,模型预测的切削力较好地反映了切削力随切削参数的变化,12组预测值的平均百分比误差分别为5.9%和7.3%,预测精度与平均值模型不一致,这可能是因为多个模型之间的误差累计导致,但是非等分模型预测的切削力的整体趋势与观测值吻合较好,这对于预测剪切区微观结构演化的参数输入(应变场和温度场分布)至关重要。通过迭代得到的剪切区热扩散的比例R如图13的次纵坐标所示,R值在0.2～0.3之间,其随着切削速度和进给的增大而增大,随着前角的增大而减小,这是因为热扩散的比例R随着温度的升高而增大导致。

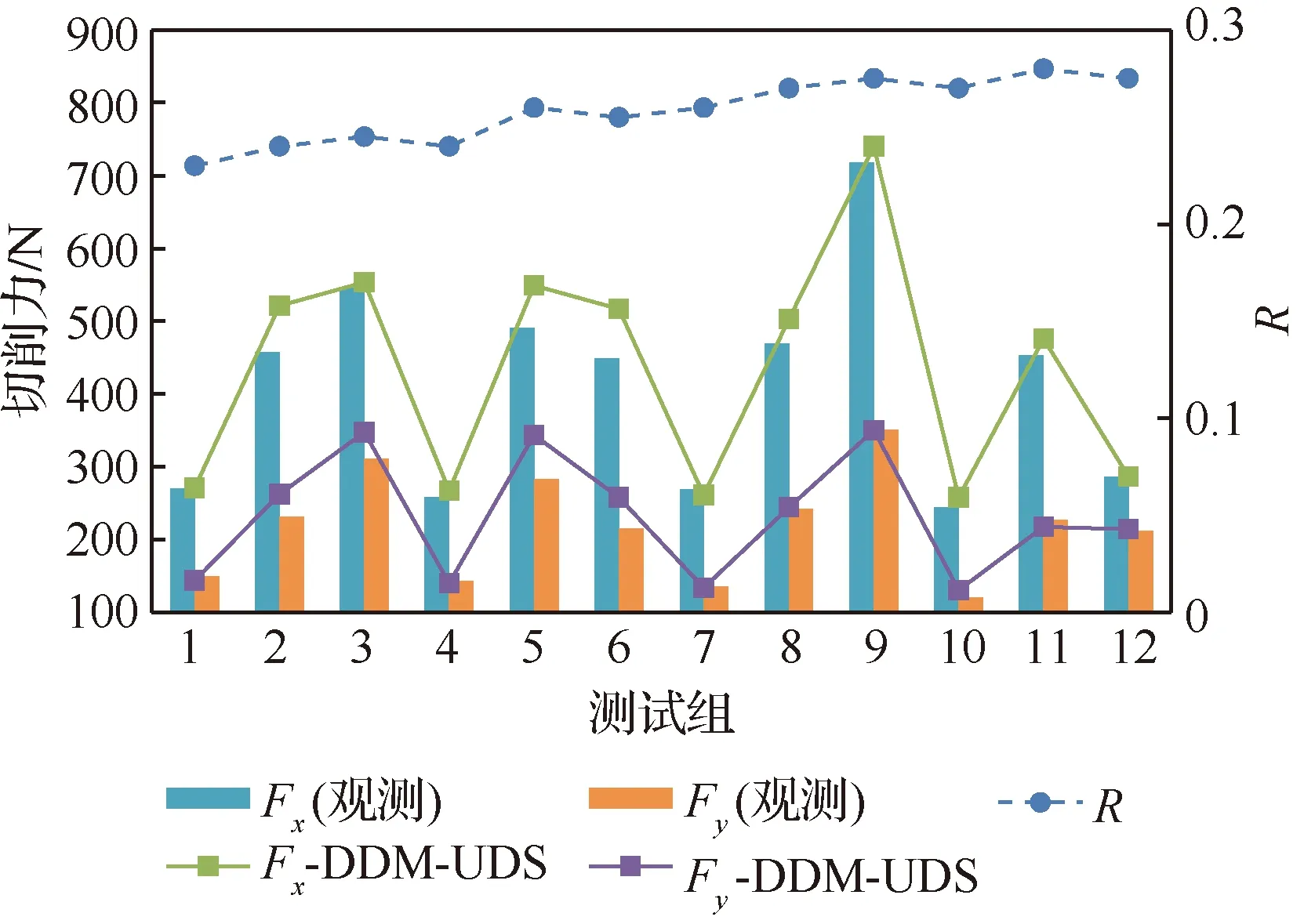
图13 非等分剪切区模型的切削力和R的预测Fig.13 Prediction of cutting force and R for unequal division shear zone model

4.2.3 解析模型与有限元模型的比较

在第7组实验切削参数下(V=90 m/min),使用Deform有限元软件建立了切削仿真模型,首先将刀具固定,然后工件往切削速度相反方向运动,为了避免刀尖周围的大变形导致的网格畸变,将网格结构视为四面体,使用拉格朗日网格技术对工件进行网格划分,热传导系数和摩擦系数使用Deform专业切削模块推荐的0.02 m2·s·K和0.6,材料模型为JC模型,参数来源文献[7]。

在有限元模型的未切削厚度层上定义了6个跟踪点,如图14(a)所示,观察到剪切区温度和剪切应力的变化过程如图14(b)和图14(c)所示,6个跟踪点的最大温度范围在140～165 ℃之间,最大剪切应力范围为224～237 MPa。解析模型预测的温度和剪切应力分布如图12所示,最大温度约为150 ℃左右,最大的剪切应力值约为230 MPa,本文预测的剪切区温度和剪切应力的最大值与有限元模型预测的结果较接近。

为了比较解析模型与有限元模型的精度,使用有限元模拟了不同的切削深度(第7、第8和第9组实验)下的切削力值,得到如图15所示的仿真结果对比,其中Error_Fx-SIM和Error_Fy-SIM是3种解析模型的平均百分比误差的平均值,Error_Fx-FEM和Error_Fy-FEM是有限元预测的百分比误差,3种解析模型得到切削力值在整体上预测精度优于有限元。有限元预测的径向力随着切削深度的增大而降低,趋势与实验值相反,Javidikia等[32]在有限元预测时也得到了相似的结果,而解析模型预测的切削力与实验值的趋势一致。获取稳态切削时的切削力值时,有限元预测时间为4～6小时,而3种解析模型预测切削力需要1～5分钟。其中耗时最少的为第1种,Oxley模型与JC模型的结合。其次为第2种,Oxley模型与DDM模型的结合。最后是第3种,等分剪切区和非等分剪切区的结合。因为JC模型计算材料行为时,计算量较少,如式(30)所示。而DDM考虑的因素较多,如式(1)～式(12),非等分模型计算切削力在等分模型的基础上还需要式(36)～式(45)迭代计算。但是,正是因为考虑了更多微观结构影响和剪切区非等分的分布特性,使得第2种模型和第3种模型的切削力预测精度分别得到了提高。

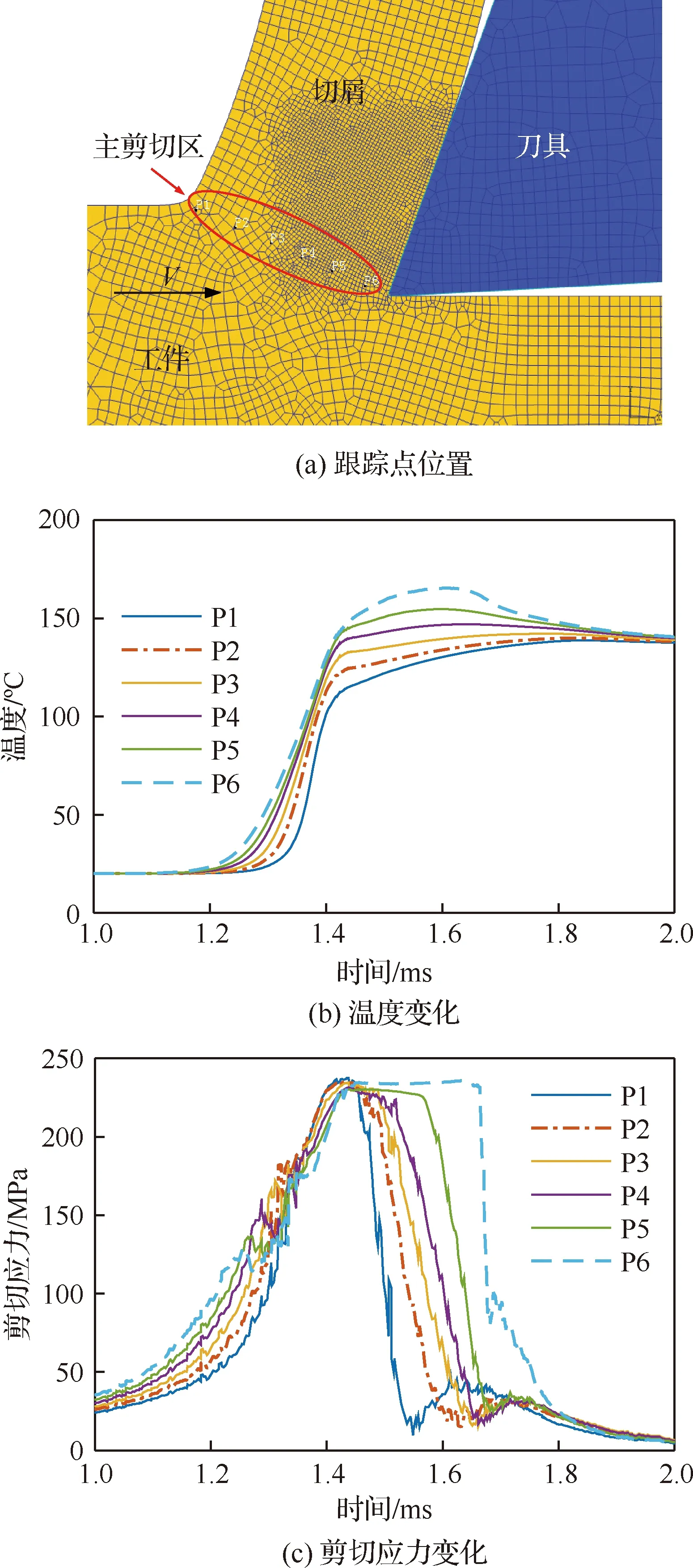
图14 有限元仿真模拟的温度和剪切应力Fig.14 Temperature and shear stress simulated by finite element simulation

4.2.4 剪切区微观结构演化预测

在切削大塑性变形过程中,由于第一剪切区剪切变形作用,应变的大量累积以及由此引入的一系列位错运动是切屑晶粒细化的主要原因。微观结构的变化与位错密度密切相关,可以通过DDM方法[7]进行解析分析,结合Oxley剪切区等分模型和非等分模型计算的应变场、温度场,可以建立剪切区微观结构演化解析模型。

图16为第3组实验切削6061-T6铝合金的主剪切区微观结构演化过程,当材料质点从入口边界处进入剪切区并经过剪切变形后到达出口边界,切屑位错密度达到了2.8×109mm-2,平均晶粒尺寸细化到569 nm,通过实验观测得到的晶粒尺寸为591 nm,实验初步验证了模型的可行性。材料在最初未受到剪切时,材料变形并不均匀,组织中的晶粒也大小不一,由于纯剪切变形的作用,材料中的粗大晶粒发生剪切和破碎,使原来粗大的晶粒沿剪切变形方向被拉长成条带状晶粒,如图9(a)所示,同时,应变逐渐增大导致材料中大量位错出现在晶粒内,由于位错运动形成亚晶界,此时剪切变形作用对晶粒细化起主要作用,随着应变的增加,晶粒逐渐细化,局部组织中出现了少量细小的等轴晶,但晶粒的大小和形状不均匀。通过剪切区后,回复作用逐渐明显,位错的增殖和湮灭将达到动态平衡,晶粒的大小基本上不再变化。

图15 不同模型的切削力对比Fig.15 Comparison of cutting forces of different models

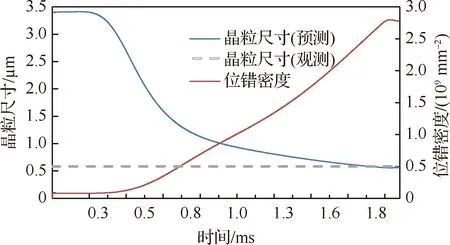
图16 剪切区位错密度和晶粒尺寸的演化Fig.16 Evolution of dislocation density and grain size in shear zone

5 结 论

1) 以位错运动为塑性变形机制引入到预测加工理论的切削力求解过程,得到了与经典切削理论相一致的力学行为且产生了更为准确的结果。

2) 当切削深度增大,切削力增大的主要原因是由于剪切区长度变长导致参与位错滑移的材料增多。增大切削速度导致切削力的降低不是单一变量引起的,而是剪切角增大、剪切区温度升高和变形区应变降低的共同作用结果。

3) 非等分剪切区模型正确反映了第一变形区温度和应力的分布特征,且与二维有限元模型分布相一致,通过实验观测初步验证了微观结构演化模型在解析切屑内位错密度和晶粒尺寸演化过程的可行性。