复杂环境下考虑动力学约束的翼伞轨迹规划

孙昊,孙青林,*,滕海山,周朋,陈增强

1. 南开大学 人工智能学院,天津 300350 2. 北京空间机电研究所,北京 100094 3. 航天科技集团有限公司 航天进入减速与着陆技术实验室,北京 100094

翼伞系统因其负载能力强、飞行稳定、飞行方向可控等优势[1-3],在航天器回收、物资空投[4-6]等军用、民用领域具有不可替代的重要作用。而在翼伞的主要应用中,必须实现精确的归航控制,确保翼伞可将负载中所搭载的物资安全投送至指定目标位置[7]。因此,需要在轨迹规划中计算出精确、可行的目标轨迹。

已有学者针对多种控制目标与约束条件,进行翼伞系统的轨迹规划研究。如文献[8]采用传统高斯伪谱法,针对控制量最优、精确着陆、迎风雀降等多约束条件,进行了翼伞归航任务中的轨迹规划研究；文献[9]所规划的轨迹均设定为参数可变的多条贝塞尔曲线,并重点研究了如何应用固定形状的轨迹消除回收落点误差的研究；文献[10-11]基于质点模型,采用蒙特卡洛仿真法计算大量规划轨迹,并通过对比分析,从中选取回收精度最高的轨迹；文献[12]则基于快速扩展随机树算法,在轨迹规划中考虑了较大风场的干扰；文献[13]探索了翼伞系统的分段轨迹规划策略,轨迹全部为标准直线或圆形；文献[14-15]采用虚拟结构法计算多个翼伞的目标轨迹,并基于李雅普诺夫稳定性设计引导策略,实现多翼伞编队；文献[16]采用一种线目标的规划策略,针对大型翼伞在空投回收中的分段轨迹规划进行了研究；文献[17]针对三自由度翼伞模型, 采用控制变量参数化与时间尺度变换相结合的优化算法对其最优控制问题进行数值求解。

通过分析现有研究,可以看出在翼伞轨迹规划中所通用的传统质点模型难以体现翼伞真实控制量与系统速度间的非线性关系。但真实翼伞通过柔性伞衣提供升力,尤其在伞衣后缘下偏的水平控制状态下,伞衣的柔性形变更加明显,导致系统存在复杂气动特性与非线性特征[18-20],在飞行过程中其水平速度与垂直速度均会受到环境、控制量状态影响,导致其运动轨迹存在时变的动力学约束,而这种动力学约束难以通过质点模型进行表述,所规划轨迹常与翼伞的实际运动状态产生较大差异,无法实现精确的归航控制。因此,在轨迹规划中采用高自由度动力学模型是计算满足系统动力学约束的目标轨迹的必然趋势。但高自由度动力学模型的复杂度高、非线性明显。因此,若仍沿用传统算法,即使在不考虑地形干扰的情况下都难以保证规划轨迹平滑、稳定。但在翼伞进行实际飞行任务中,其轨迹规划还必须针对实际任务中的复杂地形干扰进行考虑,实现精确的地形规避。

针对上述问题,本文在实现控制量最优、落点精确、地形规避等传统多约束条件的基础上,在轨迹规划中引入了翼伞系统的动力学约束。本文将建立翼伞系统的精确6-DOF(Degree of Freedom)动力学模型,通过对翼伞的6-DOF模型进行推导,将动力学模型引入到系统的状态更新矩阵中,计算翼伞偏航角的变化率与实际控制量(伞衣后缘下偏量)的非线性关系[21],通过其状态更新矩阵中的非线性动力学方程计算翼伞在飞行中的运动状态,确保所规划出的飞行轨迹也就可以满足翼伞的动力学约束。随后,针对高自由度动力学模型与改进传统高斯伪谱法,设计基于分段节点规划、离散点初次规划、离散点自重构的三阶轨迹规划策略,最大限度地保证规划轨迹的稳定性。最后,在仿真实验中与传统轨迹规划算法相对比,验证所提出算法的有效性与先进性。本文第1节介绍了翼伞6-DOF动力学模型；第2节介绍了基于改进高斯伪谱法的轨迹规划策略；第3节为仿真实验验证与分析,第4节为结论。

1 翼伞系统建模

如图1所示,翼伞由伞体与负载两部分组成。目前已有大量学者针对翼伞系统的建模进行了相关研究[22-23],而本文中为确保规划轨迹满足翼伞的动力学约束,有必要在轨迹规划中考虑翼伞的角速度变化率,尤其是偏航角的角加速度[24-25]。

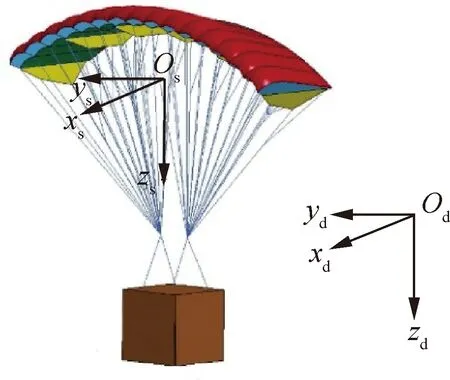
图1 翼伞系统及相关坐标系Fig.1 Parafoil system and related coordinates

同时,由于高自由度动力学模型更加复杂、计算量大,在选取模型时还需考虑有限时间内的算法收敛。综上所述,本项目将采用翼伞的6-DOF动力学模型。

1.1 坐标系转换与系统状态

在翼伞的6-DOF模型中,存在伞体坐标系与大地坐标系。在建模中,大地坐标系与伞体坐标系下的运动速度之间的关系可以表示为

(1)

式中：[x,y,z]表示系统在大地坐标系三轴下的位置；[Vx,Vy,Vz]表示体坐标系三轴下的速度；Td-s表示大地坐标系到伞体坐标系下的转换矩阵,该转换矩阵可表示为

(2)

式中：[φ,θ,ψ]分别表示大地坐标系下的翻滚、俯仰与偏航角；cx≡cosx；sx≡sinx。

而系统在大地坐标系下的三轴角速度[φ,θ,ψ]可表示为

(3)

式中：[Wx,Wy,Wz]表示体坐标下的三轴角速度；tx≡tanx。

而在6-DOF模型中,体坐标系下的翼伞系统状态将由其受力推导获得,可表示为

(4)

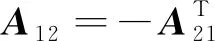
1.2 系统的质量矩阵与受力分析

式(4)中,系统的质量矩阵可表示为

A11=msI3×3+ma

(5)

(6)

(7)

(8)

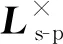
而式(4)中的系统受力可表示为

(9)

(10)

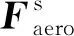
式(9)中,伞体与负载的气动力计算最为复杂。在伞体的气动力计算中一般将伞衣沿展向分为8个部分,并将其视为刚体,分别计算气动力后再进行合并。伞体与负载的气动力可表示为

(11)

(12)

式中：Cd为负载的气动阻力系数；ρ为空气密度；Sw为负载的特征面积；i=1,2,…,8表示伞衣分片；k表示不同伞衣分片的气动系数；Cli表示伞衣各分片的升力系数；Cdi表示伞衣各分片的阻力系数；Si表示各分片的特征面积。

如图2所示,翼伞通过伞衣后缘下偏,改变的伞体气动力,并以此控制其飞行方向。式(12)中,伞体的升阻力系数由伞衣后缘下偏量、迎角等因素推导得出,可表示为

(13)

式中：α表示迎角；ul、ur分别表示翼伞的左右下偏量。

结合式(1)～式(13),即可建立翼伞的6-DOF动力学模型。在动力学模型中,翼伞的翻滚、俯仰以及偏航角速度被视为系统状态,由系统受力推导得出。此外,基于式(12)～式(13),也可推导出翼伞控制量与伞体气动力的非线性关系,可精确计算伞衣后缘下偏状态下的偏航角变化率。

图2 伞衣后缘下偏Fig.2 Flap deflection of canopy

2 轨迹规划策略

2.1 基于动力学模型的状态更新矩阵推导

翼伞的传统质点模型可表述为

(14)

式中：vxy、vz表示翼伞的水平和垂直速度；[vwx,vwy]表示水平方向上的风场信息。

从式(14)中可以看出,质点模型中系统只存在水平、垂直速度与偏航角速度这4个状态,控制量与偏航角间为简单的线性关系,难以表述翼伞复杂的气动特性,因此根据质点模型所规划出的轨迹也就无法满足翼伞的非线性动力学约束。因此,本文将采用翼伞6-DOF动力学模型进行轨迹规划,与质点模型不同,在规划中系统存在12个状态：

X=

(15)

状态包含大地坐标系下的系统位置[x,y,z]、欧拉角度[φ,θ,ψ]、体坐标系下三轴的速度与角速度。而系统的状态更新矩阵可设计为

(16)

式中：T表示采样频率。

而式(16)中,大地坐标系下的系统状态可由式(1)～式(3)推导得出,可表示为

(17)

(18)

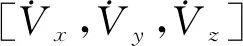
2.2 高斯伪谱法

高斯伪谱法可将复杂环境下的翼伞轨迹规划问题转化为一系列非线性参数规划问题[26],并进行离散求解,该方法也被广泛地应用于各类航天器的轨迹规划[27-28]。因此,本文将基于高斯伪谱法,针对翼伞的高自由度动力学模型进行轨迹规划。在高斯伪谱法中,一个规划问题可被表示为

(19)

系统的状态更新需要满足其动态方程：

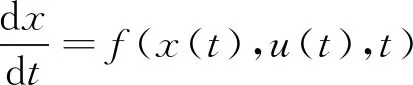
(20)

系统的状态与控制量还需满足边界等式约束与路径不等式约束：

φmin≤φ(x(t0),t0,x(tf))≤φmax

(21)

C(x(τ),u(τ),t0,tf)≤0

(22)

随后,将连续的系统状态离散于多个离散点处,并计算离散点处的系统状态,以进行轨迹规划。为此,将引入时间变量,把高斯伪谱法中的所规划的离散点分布从实际时间[t0,tf]转换于[-1,1]：

(23)

通过式(23),即可将离散点的分布从真实时间[t0,tf]转换至[-1,1],并将离散点的位置设计为N阶勒让德-高斯配点(LG配点),即N阶勒让德多项式的零点。假设离散点为[τ1,τ2,…,τk,…,τN],则勒让德多项式可表示为

(24)

式中:d为勒让德多项式系数。

如式(19)～式(24)所示,传统轨迹规划算法首先计算各离散点处的系统状态,并将所有离散点相连,获得对应的规划轨迹。而在传统算法所通用序列二次规划法中,首先将基于式(24)在所规划的整体时间范围内选取一定数量的离散点,并通过模型推导计算此类离散点处的系统状态。随后将采用内点法、插值法等方法直接插入第2阶段的离散点及其所处位置的系统状态,最后将所有离散点连接在一起,形成规划轨迹。该方法广泛应用于传统质点模型的轨迹规划,但在采用高自由度动力学模型后,第2阶段的离散点无法满足翼伞的动力学约束,易令优化轨迹出现震荡,导致规划失败。因此,有必要针对高自由度动力学模型在轨迹规划中进行针对化设计[29-30],最大限度地保证规划轨迹的稳定。

2.3 分段轨迹规划策略与多约束条件

如图3所示,本文将针对翼伞的高自由度动力学模型,设计一种三阶的轨迹规划策略,3个阶段分别是：分段点规划、离散点初次规划以及离散点自重构。

首先,将翼伞的整体运动轨迹分为多个段落,设定较少的离散点作为分段节点,计算多个分段节点处的系统状态信息,先得到一条粗略、平稳的目标轨迹,防止出现轨迹震荡、错乱等问题。随后,在各个分段中分别根据式(24)选取LG配点,基于高自由度动力学模型进行初次规划,在确保轨迹满足系统动力学约束的基础上,同时实现地形规避、精确归航等多控制目标。最后,根据初次规划中的系统运动状态在各个分段中进行离散点自重构,在环境复杂、控制量波动大时提高离散点个数,平滑优化轨迹,以减少规划轨迹与实际之间的误差。针对上述结构,本文将设计分段轨迹优化策略,令优化轨迹同时满足多约束条件。

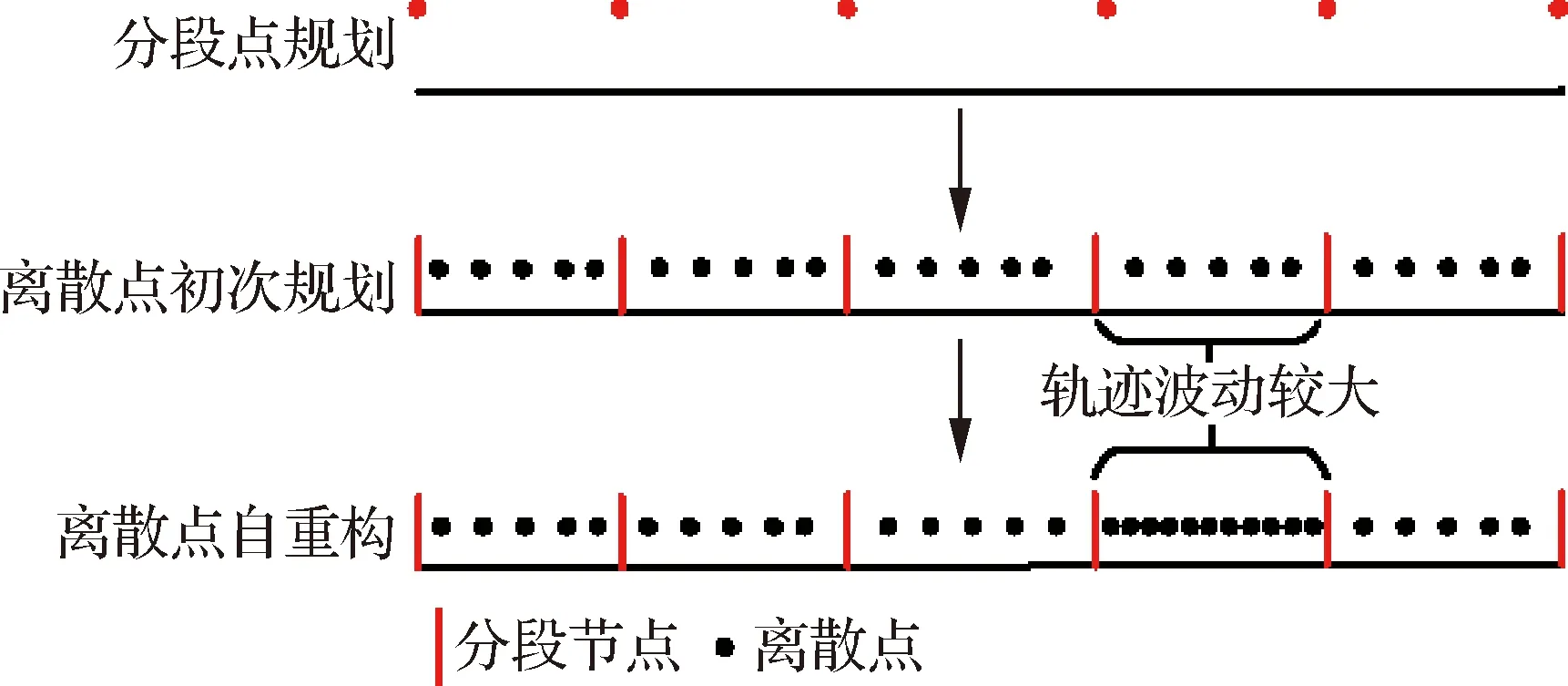
图3 针对高自由度动力学模型的轨迹优化策略Fig.3 Trajectory optimization methodology for high-order dynamic model

1) 初、终值约束

首先,本文将所规划轨迹分为多个分段,首先推导各分段点的位置,计算规划轨迹的粗略状态。各分段节点的状态可表示为

(25)

式中：Pi表示第i个分段；t0表示初始时间；X0表示初始状态；t1表示第1分段的终止时间;X1表示第1分段终止时的状态；[ti-1,f,ti,f]和[Xi-1,f,Xi,f]表示各节点的起始、终止时刻及其系统状态;tf表示终止时间。如式(25)所示,每个阶段的终止节点即为下一个阶段的初始节点。

此外,优化节点间的位置距离还需小于一定降落高度下系统滑降比所允许的最大飞行距离：

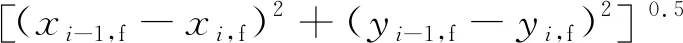
(zi-1,0-zi,0)×fgr,max

(26)

式中：fgr,max为翼伞的最大滑降比。

设定归航控制的目标点为大地坐标系的坐标原点,而翼伞的终值约束可表示为

(27)

2)控制约束

在采用6-DOF动力学模型后,轨迹规划中的系统控制量为翼伞的真实控制量,即为伞衣后缘下偏量,其控制量限制可表示为

-10≤u≤10

(28)

式(28)中,负值表示左侧伞衣后缘下偏,正值表示右侧。

3)地形规避

路径中的系统动力学已经在2.1节中进行考虑,本节中将山体设为禁飞区,着重于实现翼伞归航控制中的地形规避。首先,山体将被设计为一系列同心圆,可表示为

(29)

(30)

式中：p表示山体编号；[xp,yp]表示山体圆心的水平位置；hp表示山体的最大高度；δ表示山体的倾斜角度；Rp表示山体的半径。

基于地形规避的轨迹实时约束需满足：

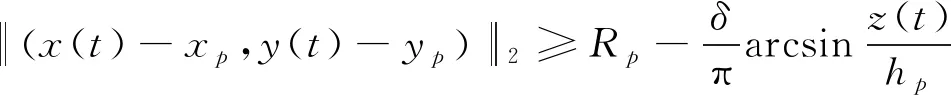
(31)

4)目标函数

在目标函数的设计中,主要考虑系统的控制量最优,可表示为

(32)

该目标函数的判定标准为令目标函数J的数值最小,该设计还可最小化系统的控制量震荡,提高轨迹的稳定性。

此外,在轨迹优化中需针对控制量过大的阶段进行离散点自重构,即在轨迹波动较大时增加离散点数量,进行二次规划。设定Jmax为轨迹波动的最大阈值,当

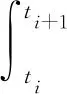
(33)

对第i段轨迹进行离散点自重构,平滑优化轨迹。

3 仿真实验

本节给出了基于不同地形条件下的仿真实例,并通过与传统高斯伪谱法相对比,验证所提出算法的有效性。所选用伞形的展弦比为1.73,伞绳长度为3.7 m,伞衣面积为22 m2,负载质量为80 kg,负载的阻力特征面积为0.5 m2。在仿真实例中,翼伞初始水平位置为[2 000, 2 000] m,初始高度为1 500 m,目标落点设定为大地坐标系原点,即[0,0,0] m。在实例1,翼伞的初始水平飞行速度设定为10 m/s,垂直速度为2 m/s,初始航向角为-145°；实例2中翼伞的速度不变,初始航向角为180°。

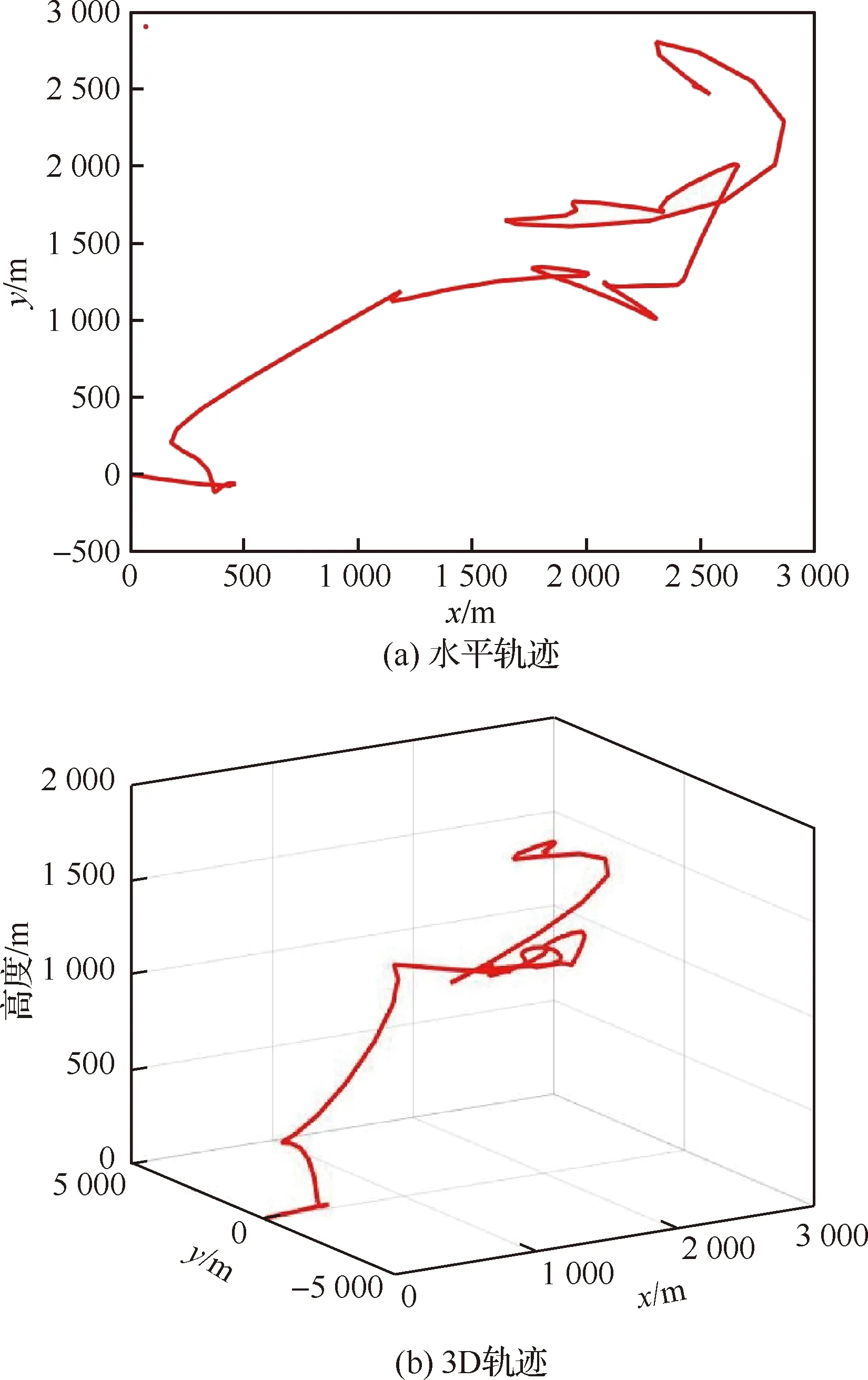
图4 基于传统高斯伪谱法与6-DOF模型的轨迹规划Fig.4 Trajectory optimization based on traditional Gauss pseudo-spectral method and 6-DOF dynamic model

首先,若仍沿用传统高斯伪谱法,基于翼伞6-DOF动力学模型的轨迹优化结果如图4所示。在传统轨迹规划中,仅给出系统的初、终值要求,并忽略了地形约束。从结果中可以看到针对高自由度动力学模型,传统算法难以获得稳定、可行的规划轨迹,更无法满足翼伞的动力学约束。虽然翼伞最终到达了目标位置,然而所规划轨迹存在明显震荡,甚至存在明显的规划错误。

图5～图7中则给出了基于改进后高斯伪谱法与翼伞6-DOF模型的仿真结果。在仿真实例1中,存在两个山峰地形,山峰的高度为1 500 m,山峰地形的圆心为[1 000,1 000] m和[1 700,1 700] m,山峰最大半径为250 m和300 m。从图5(a)和图5(b)可以看出,改进后轨迹规划策略可在满足系统动力学约束的基础上,计算出一条较为平滑、稳定的规划轨迹,轨迹稳定性相比于传统算法有着较大的提高,还可针对不同高度下的禁飞区(山峰)半径实现有效的地形规避。从图5(c)和图5(d)中也可以看出在进行着陆与地形规避时外,翼伞控制量可保持稳定,并实现有效的偏航角控制。

在初次规划后,离散点在一些波动较大的轨迹分段内的数量较少,导致目标轨迹的偏航角变化率过大,不够平滑。但由于翼伞存在大惯性的特征,难以跟踪角速度变化率过大的转弯轨迹。而如图6所示,通过分析初次规划的轨迹后,可在偏航角变化率过大的分段内进行离散点自重构,优化离散点分布,增加轨迹波动较频繁的区域的离散点数量,进行二次规划,提高优化轨迹的平滑度。

图7则给出了翼伞在体坐标系下的角速度信息,系统的角速度均由6-DOF动力学模型推导得出,在轨迹规划中基于系统的角速度与速度信息计算规划轨迹,可确保规划轨迹满足翼伞的非线性动力学约束。实例2中设计了5个山峰,圆心分别为[1 500,1 500] m、[1 700,900] m、[800,1 100] m、[1 200,800] m、[500,500] m,半径为400 m或350 m,山峰的高度均为1 500 m。并在仿真中引入突风干扰,突风速度为2 m/s,风场方向为x轴负方向,持续时间10 s。

图5 仿真实例1Fig.5 Case 1

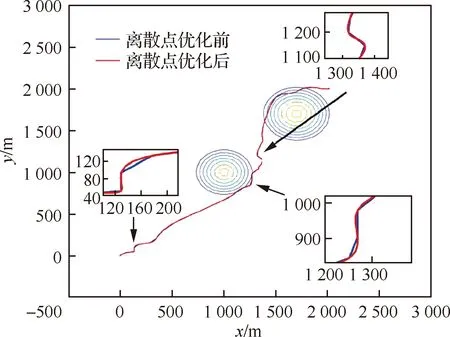
图6 离散点自重构后的规划轨迹Fig.6 Planning trajectory with discrete point self-reconfiguration

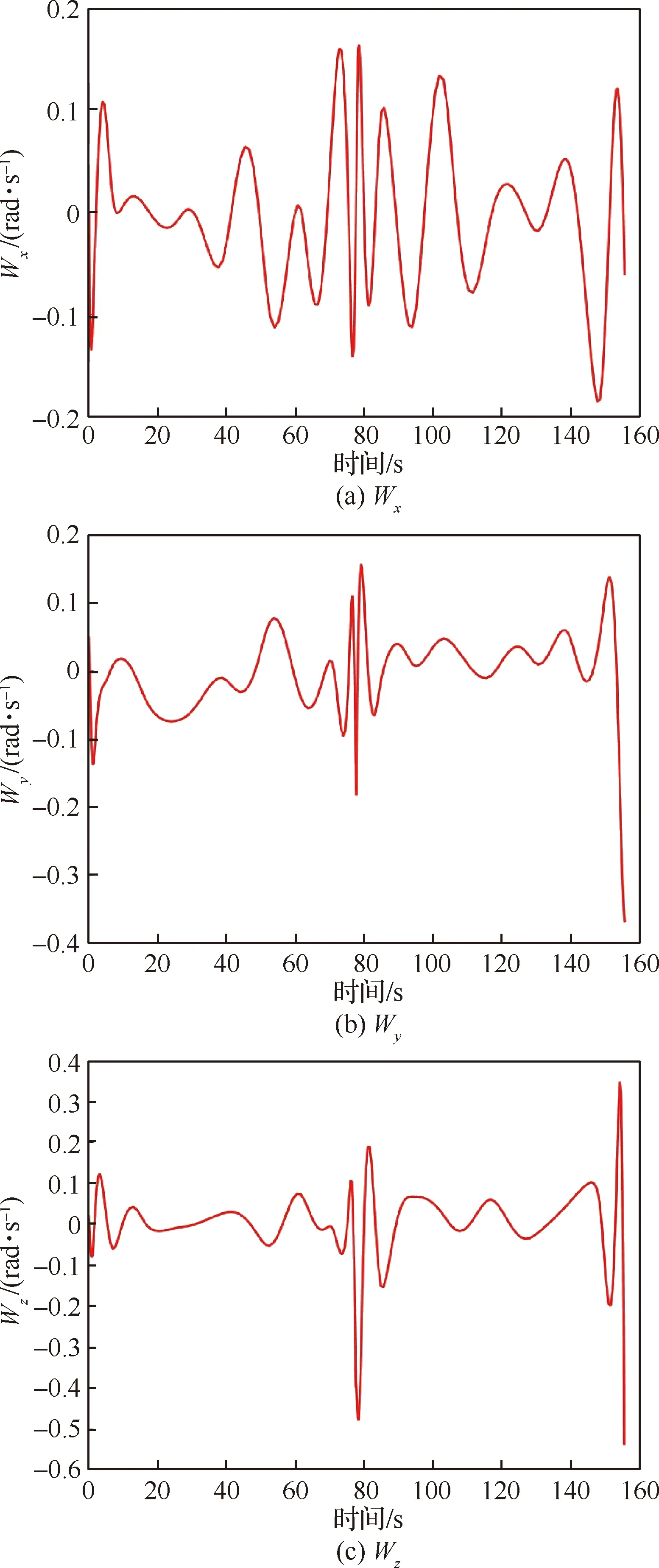
图7 翼伞系统的角速度状态Fig.7 Angular velocity of parafoil system

仿真实例2实验结果如图8所示。从仿真实验结果中可以看出所提算法可以有效地针对复杂地形进行轨迹规划,所得轨迹较为平滑。同时,图8(a)中黑框处即为突风干扰下的规划轨迹,可以看到由于突风干扰,伞体在一定时间内出现了向左的偏转,但很快便通过控制量变化恢复稳定,具备一定的鲁棒性。此外,由于采用了6-DOF动力学模型,系统可通过控制量变化、转弯等因素调整其滑降比,因此无需通过盘旋消耗其赘余高度。同时,为确保在采用6-DOF模型后还能维持飞行轨迹稳定,在本文目标函数的设计中也期望能最小化系统偏航角与控制量的波动,因此在一些复杂的地形下本文所提算法也可通过平滑、稳定的飞行轨迹到达目标位置。

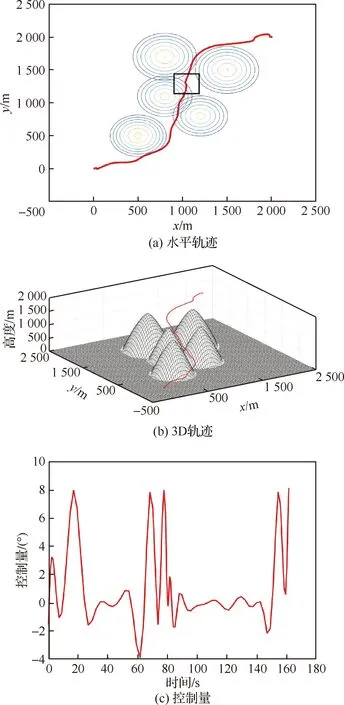
图8 仿真实例2Fig.8 Case 2

4 结 论

针对翼伞系统的归航控制,本文提出了一种考虑系统动力学约束的轨迹规划策略。相比于3-DOF简单质点模型,本文不仅在轨迹规划中引入翼伞的6-DOF动力学模型,还针对传统轨迹规划算法难以计算出基于高自由度动力学模型的平稳轨迹的问题,对传统算法进行改进,提出了一种多阶段的改进后高斯伪谱法,将轨迹规划分为3个阶段,即分段点优化、离散点初次优化以及离散点自重构,最大限度地保证优化轨迹的平滑、稳定,并结合翼伞的6-DOF动力学模型,在实现精确归航、地形规避等约束条件的基础上,确保规划轨迹可以满足翼伞的非线性动力学约束,提高规划轨迹在真实飞行任务中的可实现性。

目前,由于模型非线性强且实验室所用计算机的计算能力尚有提升空间等原因,规划轨迹仍不够平滑,可能出现一些转角过大的拐点。因此,如何彻底消除这些拐点,计算出更加平滑的轨迹,也是下一阶段研究的重点研究方向。