切换非线性系统的指数拟无源化及其镇定

檀胜男，庞洪博

（辽宁工业大学 理学院，辽宁 锦州121001）

0 引言

20世纪70年代，WILLEMS[1]首次提出无源性概念.一般来讲，无源系统内部消耗的能量不超过外部供给的能量.无源理论在电力、机械等工程实践中有都着广泛的应用.无源系统的储存函数通常可以作为一个备选Lyapunov函数.因此，一旦确定了无源性，就可以解决系统的稳定性和镇定问题[2].然而，并不是所有系统都是无源的，文献[2]提出了反馈无源化条件，将无源理论与非线性几何理论结合起来，解决了仿射非线性系统的反馈无源化问题.文献[3]提出了指数无源理论，并给出了非线性系统反馈指数无源化条件，即要求相对阶为1和最小相位. 因为实际系统往往存在较大的不确定性和干扰，所以精确的反馈无源化往往无法实现.因此，文献[4]～文献[7]提出了“实用”无源性的概念，如：拟无源、半无源和集合无源.拟无源性是一种比无源性更普遍的概念.与无源系统相比，拟无源系统可以包含具有有限功率的能量源.该概念已经应用在含有非无源或负荷的电力系统稳定性分析中[8]，即在网络中某些负荷或串联元件非无源的情况下，当满足类能量约束时，利用拟无源性概念得到了最终有界性.文献[7]对于特定选择的有限增益供给率，利用拟无源性得到所谓的有限功率增益稳定性.

作为一类特殊的混杂系统，切换系统由有限个连续时间子系统和切换规则组成.切换系统在实际中具有广泛的代表性，许多实际系统，如航空航天控制系统[9]、电力系统[10]等，都可以建模为切换系统.由于离散动态和连续动态相互作用，使切换系统具有更加复杂的行为，因此切换系统的稳定性分析和镇定问题也更加困难.目前研究切换系统稳定和镇定问题的方法有很多，如共同Lyapunov 函数方法[11-13]，多Lyapunov 函数方法[14-19]，平均驻留时间方法[20-24]等.

非线性系统无源理论已很完备，但对于切换系统仍有很多问题值得研究.文献[25]利用共同存储函数来研究切换非线性系统的无源性.由于许多切换系统可能不存在或很难找到共同的存储函数，所以每个子系统有自己的存储函数是更合理的.因此，文献[26]、文献[27]提出了多存储函数多供给率方法，建立了切换非线性系统耗散理论框架，并解决了切换系统的稳定性分析和镇定问题.迄今为止，针对切换系统，研究拟无源性的文章鲜有报道.文献[28]采用平均驻留时间方法，利用子系统的拟无源性，获得了切换非线性参数不确定系统的实用稳定性. 文献[29]利用多存储函数多供给率方法获得了拟无源切换系统的轨迹最终有界性，但没有考虑系统的拟无源化问题.文献[30]利用多存储函数方法， 研究了切换非线性系统的拟无源性和反馈拟无源化.设计了依赖于状态的切换信号和状态反馈控制器，但没有考虑系统的稳定性.

本文解决切换非线性系统的指数拟无源化及其镇定问题.与现有结果比较，本文创新之处在于：第一，提出了切换非线性系统指数拟无源概念.与文献[29]相比，这种无源性不要求子系统工作时的拟无源性，仅要求切换系统整体拟无源性；第二，将拟无源化方法和Backstepping技术结合，构造性的设计依赖于状态的切换律和反馈控制器，解决切换非线性系统的镇定问题，克服相对阶为1和最小相位的限制.与非切换系统比较，难点在于每一步设计共同的反馈控制器；第三，受最大域函数方法启发，提出新的切换律设计方法，与最小切换律比较，为切换律设计提供更大自由度.

注Rn为n维欧几里得空间；如果连续函数α:[0,∞)→[0,∞)严格增长，且α(0 )=0，则α属于K类函数. 如果α=∞，且当r趋于无穷时α(r)趋于无穷，则α属于K∞类函数；对于连续函数β: [0,α)×[0,∞)→[0,∞)，如果对于每一个固定的s，映射β(r,s)是关于r的K类函数，并且对于每个固定的r，映射β(r,s)是s的递减函数，且当s趋于无穷时β(r,s)趋于零，则β属于KL函数.

1 问题描述及预备知识

式中，t0为初始时间，x0为初始状态，N为非负整数集. 当时，σ(t) =ik，即：第ik子系统工作的时候，切换系统（1）的轨迹x(t)为子系统ik的轨迹.此外，假设系统的状态在切换时刻不发生跃变，即：轨迹x(t)是处处连续的，且无滑模现象发生.

定义1考虑切换系统（1），对于给定的切换信号σ(t)和，如果存在常数αi和非负函数，使不等式

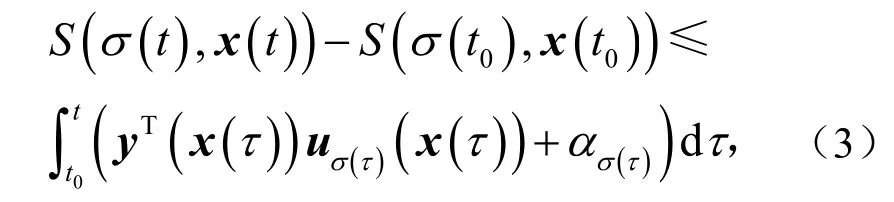
成立，称系统式（1）是拟无源的[25].

定义2考虑切换系统（1），对于给定的切换信号σ(t)和，如果存在非负函数，常数αi≥0，λ＞0，满足下列不等式

称系统式（1）是指数拟无源的.

注αi可看成第i个子系统产生的能量.由定义1和定义2可看出，当λ=0时，式（4）为拟无源不等式.并且当αi=0时，定义2退化为切换系统无源性定义[27]. 因此，定义1相比于切换系统无源的定义是更一般的.按照定义2，不要求子系统在激活状态时具有指数拟无源性，而仅要求切换非线性系统整体的指数拟无源性.

为了研究系统的镇定问题，下面提出实用稳定性概念.

定义3考虑系统式（1），对于给定的切换信号σ(t)，设计控制器ui，如果存在KL类函数ϑ(⋅)，K∞类函数ζ(·)和正常数χ使不等式

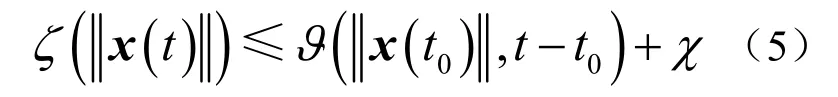
成立. 那么闭环系统（1）是实用稳定的.

注从式（5）可以看出：

（1）当t→∞时，系统轨线x(t)最终进入半径为ζ-1(χ)的球内.

（2）对于每个ε＞χ，都存在δ=δ(ε)＞0，满足

因此，定义3与一般的实用稳定性定义等价[28]. 如果χ=0，将退化成渐近稳定性定义[31].

2 主要结果

本节研究指数拟无源系统稳定性，并给出无源化条件.

定理1假设系统（1）是指数拟无源的，如果存在正定的连续函数，K∞类函数ι1(⋅)和ι2(⋅)，有

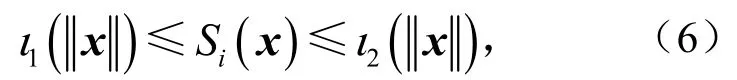
那么系统式（1）在控制器ui=-φi(y)作用下是实用稳定的，其中φi(y)是连续函数，满足φi(0 )=0且yTφi(y)≥0.

证明定义.对于t≥t0,,k∈N，根据指数拟无源不等式（4）和输出反馈控制器ui=-φi(y)，有

由式（6）和式（8）可得

下面研究切换非线性系统的反馈指数拟无源化问题.

考虑具有共同输出y=h(x)的系统式（1）被描述为

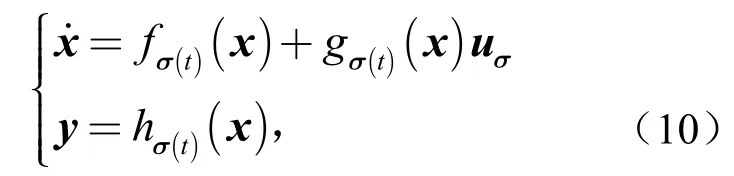
为了将系统式（10）转换成标准型，对于第i子系统，，作如下假设.

假设1矩阵L gih(x)是非奇异的，.

假设2存在一个坐标变换，满足，j=1,2,…,m，式中

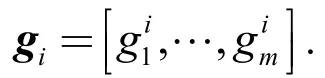
选取共同的状态变换y=h(x)和.在假设1、假设2下，系统式（10）可以转换成如下标准形式

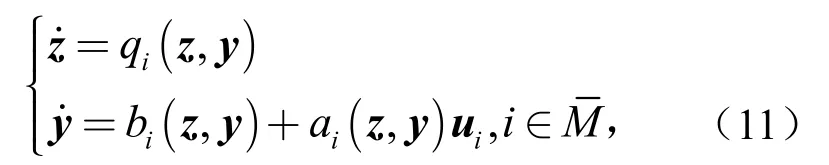
下面给出系统式（10）反馈指数拟无源化的充分条件.

定理2假设系统式（10）的所有子系统都满足假设1、假设2.如果正定的光滑函数Si(z)，连续函数Ui(z)和函数.对 于i,l∈有，βil(z)≤0，λi(z)＞0，常数αi≥0，以及下述的不等式成立

那么系统式（10）在一定的切换律下反馈等价于一个指数拟无源的切换系统.

证明在假设1、假设2下，系统式（10）可以转换为式（11）.选取存储函数

选取反馈控制器

那么，能够得到

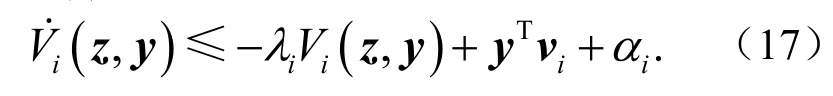
选取切换律为

将式（17）两端乘etλ并在区间[t k,tk+1)积分可得

因此，系统式（10）在切换律式（18）下是指数拟无源的.因此，系统式（10）反馈等价于一个指数拟无源系统.证毕.

注在式（13）中，当βil=0和αi=0时，式（13）退化成最小相位条件.可知，式（13）比最小相位条件更弱.

注受最大域函数方法启发，设计了切换律式（18），其中Ui仅要求是连续函数，不需要取正定的存储函数，即当Ui=Si时，切换律式（18）退化成最小切换律.

下三角结构系统是一类重要的非线性系统，在实际工程中，许多系统可以建模为具有下三角结构的系统. 即使一些系统在建模时不具有下三角结构，在满足一定的条件下，可以通过坐标变换和状态反馈转化为具有三角形结构的系统.对于具有下三角结构的系统，则意味着存在更多的手段来设计控制器.

下面利用拟无源化和反步法结合解决下三角结构系统镇定问题.

考虑如下的严格反馈切换非线性系统

式中，z∈Rq和x=(x1,…,xn)T∈Rn为系统的状态.另外，当，记，ui为第i个子系统的输入，y∈Rm为系统的输出.fci(x),gdi(x)是光滑的向量函数，其中c=0,1,…,n，d=1,…,n，且

为研究式（22）系统的指数拟无源化及镇定问题，作如下假设.

假设3存在一个正定的光滑函数S i(z)，连续函数U i(z)和函数θil≠0，光滑函数η0(z)，满足η0(0 )=0.对于有，βil(z)≤0，λi(z)＞0，常数αi≥0，有如下不等式成立

引理1考虑如下非线性切换系统

输出为y=x-η0(z)，如果假设3成立，设计如下反馈控制器

和切换信号

那么系统式（25）在切换律式（27）下是指数拟无源的.

证明通过输出y=x1-η0(z)将系统式（25）变换为

选取系统式（22）的存储函数为

对Vi(z,y)沿系统轨线求导得

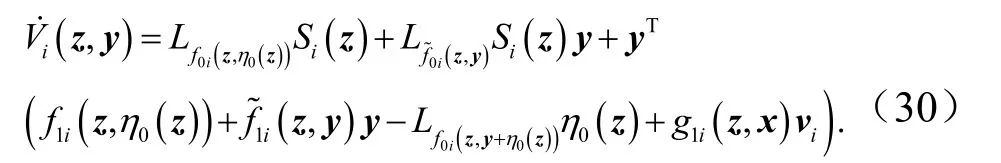
由假设3可得

将式（26）代入式（31）得

同理定理2，可得

因此，系统式（25）在切换律式（27）下是指数拟无源的.证毕.

定理3考虑切换非线性系统式（22），如果假设3成立，那么，存在一个状态反馈控制器，使得闭环系统式（22）在切换律式（27）下是实用稳定的.

证明 Step 1考虑切换非线性系统式（22）的子系统(z,x1)

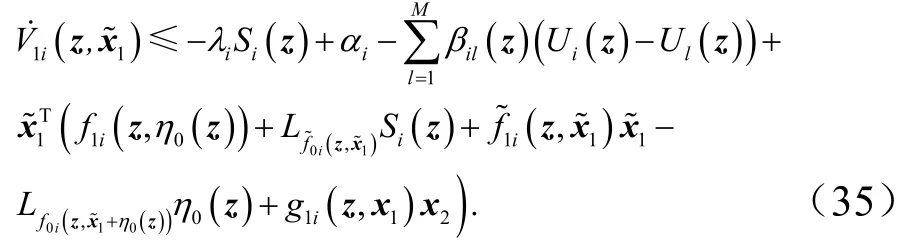
设计一个共同的反馈控制器

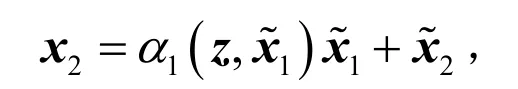
令

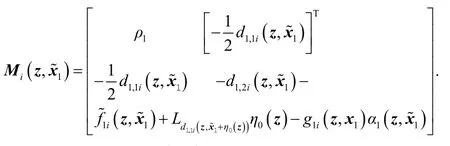
构造光滑函数α1(x1)，并满足如下不等式

这使得对于任意的z和，都有.

从而，可以得到

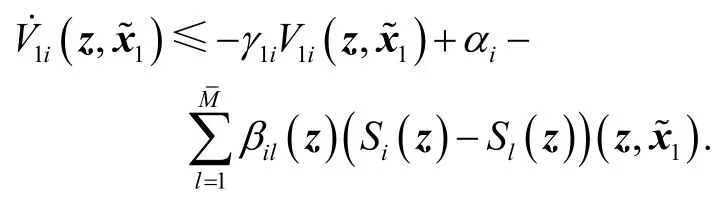
Step 2系统(z,x1,x2)可以表示为

式中，

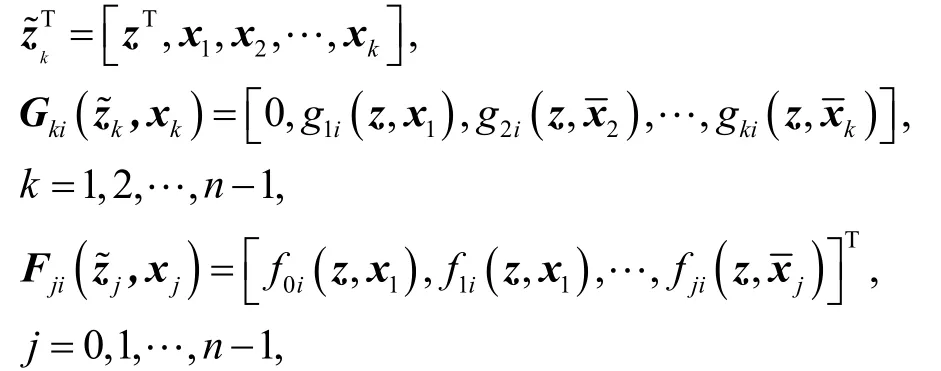
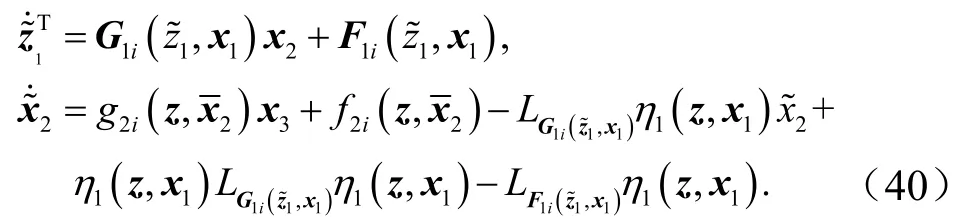
选取存储函数如下

沿式（40）轨线求导得

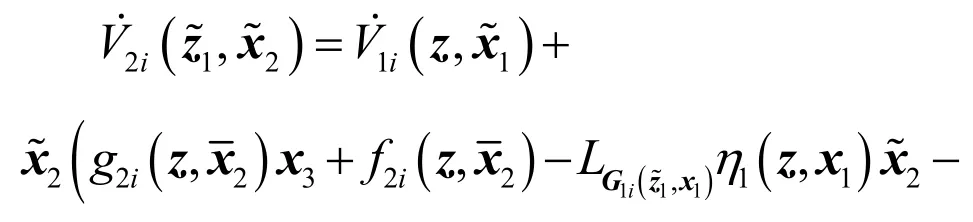
令

所以式（41）可以转换为如下形式

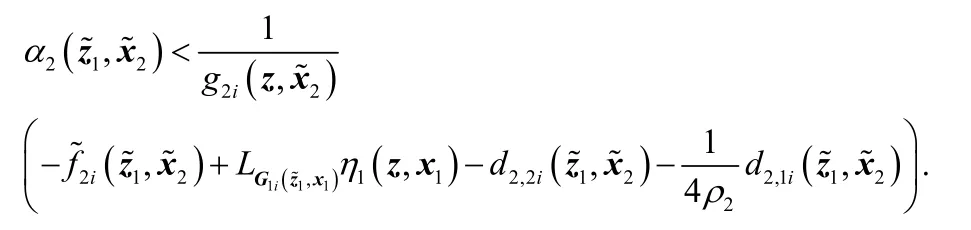
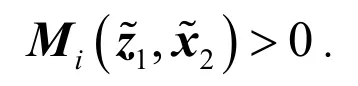
从而，可以得到

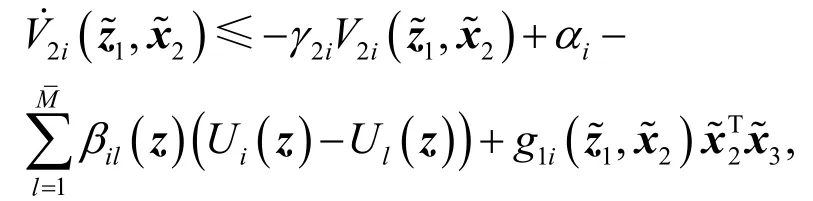
以此类推，可得在第n-1步，存在γ(n-1)i＞0有如下不等式成立

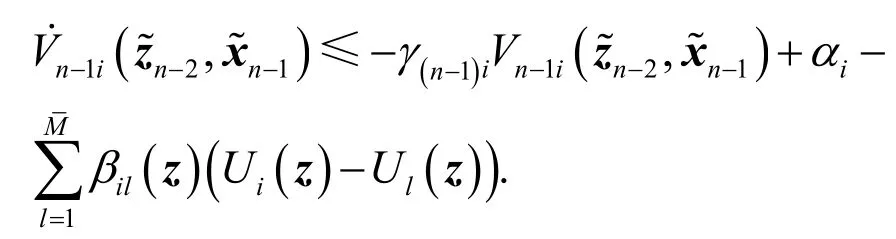
Step n系统可以表示为

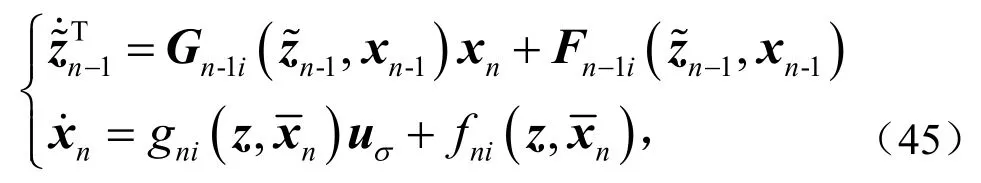
选取存储函数为

设计反馈控制器如下

因此，存在γni＞0有如下不等式成立

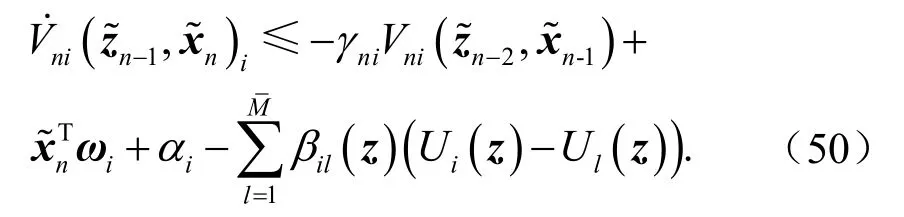
根据引理1可得，系统式（22）在切换律式（27）下是指数拟无源的.从而，由定理1可知，闭环系统式（22）在控制器作用下，是实用稳定的.证毕.

3 数值例子

通过两个数值例子来验证本文所提出方法的有效性.

考虑系统式（1）的两个子系统：

子系统1

子系统2

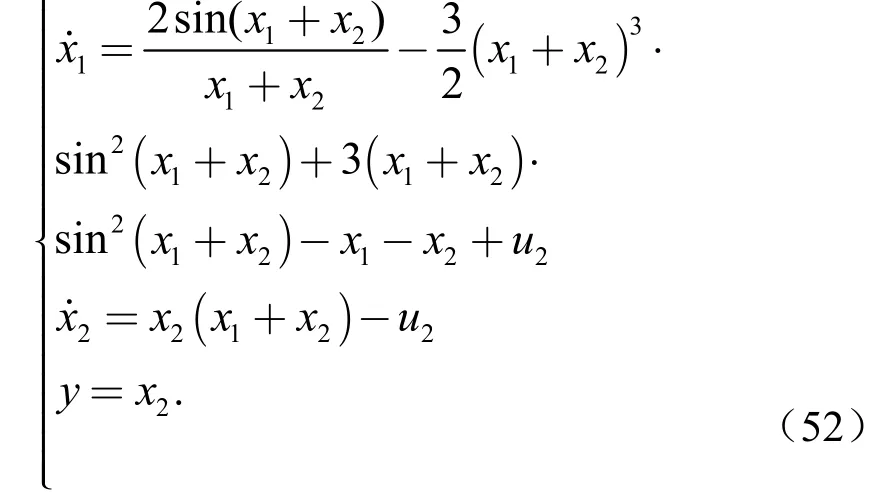
选取坐标变换

子系统分别变换为

选取函数

那么子系统的存储函数分别为

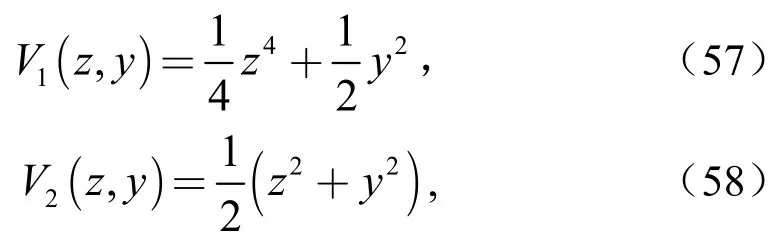
则有

反馈控制器选取为

式中，v1和v2是对应子系统的新的输入.构造切换率如下

由定理2可知，由子系统式（51）和式（52）构成的切换系统在切换率式（62）下是指数拟无源的.进一步，根据定理1可得，切换系统是实用稳定的. 选取初始状态x(0)=(-1.414,1.415,5).仿真结果见图1、图2，图1描述了闭环系统的状态.图2是相应的切换信号.

图1 闭环切换系统的状态响应Fig.1 state response of the closed-loop system

图2 切换信号Fig.2 switching signal of the switched system

考虑系统式（22）的两个子系统分别为

选取

因为

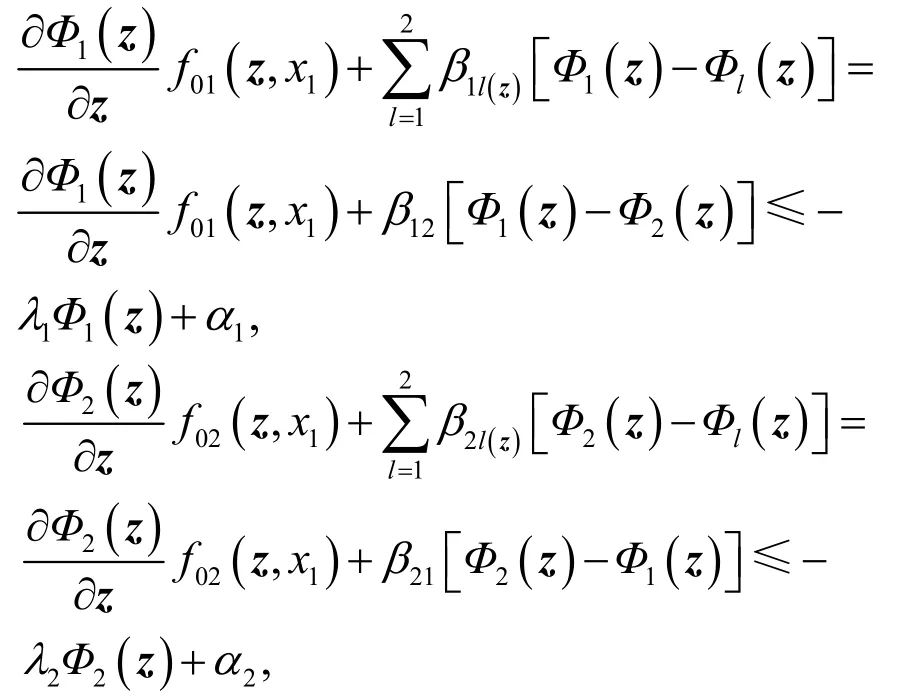
容易验证满足假设3条件.选取存储函数

对V1i(z,x1)沿系统式（51）、（52）轨线求导得,.设计共同的反馈控制器为

选取存储函数

式中，

设计切换律

根据定理3，闭环系统式（51）、式（52）是实用稳定的. 选取初始状态x(0)=(29.9,0.01,2.1,0.5).仿真结果见图3～图5.图3是系统的状态响应，可见闭环系统是实用稳定的，从而说明本文方法的有效性.图4为系统的输入控制1u和u2.图5给出了相应的切换信号.

图3 闭环切换系统式（51）、（52）的状态响应Fig.3 state response of the closed-loop system（51）、（52）

图4 控制输入Fig.4 control inputs u1 and u2

图5 切换信号Fig.5 switching signal of the switched system

4 结论

研究切换非线性系统指数拟无源化并利用所建立的理论，解决切换严格反馈系统的镇定问题.

（1）针对一般切换非线性系统，在给定切换信号下，解决指数拟无源切换非线性系统的镇定问题，获得了实用稳定性.

（2）针对一类切换严格反馈系统，将拟无源化方法和Backstepping技术结合，构造性的设计了依赖于状态的切换信号和反馈控制器，解决了切换严格反馈系统的镇定问题.

通过仿真例子验证所提出方法的有效性.