改进FA算法在阴影条件下光伏MPPT中的应用

付 华，张 彤 ，于 田，杨 傲

（1.辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105；2.国网辽宁省电力有限公司 阜新供电公司，辽宁 阜新 123000）

0 引言

目前太阳能成为重要的清洁能源，成为代替传统能源的首选.在现实应用中，光伏阵列的输出功率和输出电压会随着环境的变化而改变，在特定的电压下才能达到最大输出功率[1].找到一种有效的MPPT方法使光伏阵列达到最大的转换效率显得极为重要.

近几年提出多种MPPT算法，例如电导增量法（Incremental Conductance，INC）、扰动观察法（Perturbation and Observation，P&O）等.这些算法计算简单，追踪效果也很好，但存在一定弊端，即步长固定.当步长过大，整个系统的震荡会加剧，系统稳定性变差；当步长过小，阵列输出较低功率的时间会增加，追踪效果也会变差.当局部遮阴（Partial Shadow Condition，PSC）时，光伏电池输出特性曲线是出多峰状态的，原算法不能分辨出局部极值（Local Peak，LP）和全局最大值（Global Peak，GP），此时会发生强烈震荡并失效.因此很多学者提出了一些多峰MPPT算法，文献[2]提出P&O结合PI控制方法来提高前期收敛速度并减轻在最大功率点处的抖动问题，但也不能保证适用于复杂情况；文献[3]提出应用非线性反步长控制器进行最大功率点追踪，应用扰动观察法获得参考电压，但未考虑鲁棒性的非线性自适应控制器在外部干扰下可能导致整个系统崩溃；文献[4]提出粒子群算法（Particle Swarm Optimization，PSO）结合INC追踪最大功率点的改进算法.粒子群算法和遗传算法（Genetic Algorithm，GA）等也开始在光伏发电领域得到应用，但PSO由于其受个体最优的影响，可能在一些过低的极值点搜索较长的时间，仍存在追踪时间较长的问题；GA的局部搜索也比较差，容易导致早熟.因此多峰MPPT控制依然是亟待解决的问题.根据文献[5]提供的对P&O、INC、PSO、FA这4种算法的对比分析得知，FA在PSC条件下光伏最大功率点追踪中的速度，稳定性和效率优于其他算法.

本文提出改进FA算法的光伏阵列MPPT控制方法，追踪光伏阵列模块的最大功率点.通过与其他算法进行比较，建立仿真模型，证明其优越性.

1 光伏阵列的特性分析

鉴于计算的精准度和速度，双二极管模型是代表太阳能电池工作原理最理想的模型之一，其等效电路见图1.

图1 光伏电池双二极管模型Fig.1 photovoltaic cell double diode model

输出电流方程为

式中，

式（1）～式（3）中，Ipv为光生电流，A；I01和I02为二极管的反向饱和电流，A；UT1和UT2分别为两个二极管的热电压，V；NS为电池板元件串联数；q为电子电荷常数；k为玻尔兹曼常数；T为环境温度，℃；α1和α2分别为两个二极管的理想常数[6].

该模型精度高，但计算量较大，为了简化，文献[7]提出该模型的改进模型

式中，

仿真采用的太阳能电池板组件参数：UOC=37.7 V，Um=30.5 V，ISC=8.85 A，Im=8.2 A.该型号电池板分别在STC（参考温度是25℃，参考光照为1 000 W/m2、750 W/m2、500 W/m2、250 W/m2）和PSC的I-U和P-U特性曲线，见图2.当光伏阵列发生局部遮阴时，输出P-U曲线会出现多个LP，其中只有一个GP.

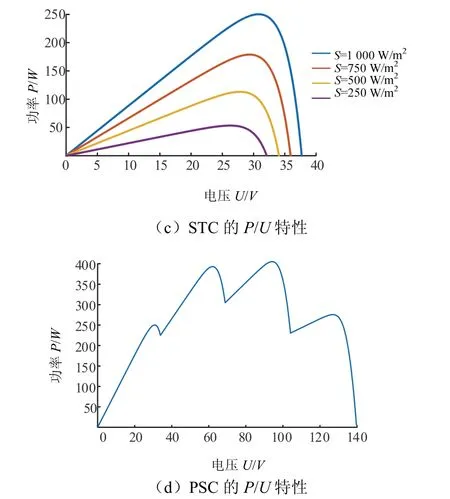
图2 STC和PSC的I-U和P-U特性Fig.2 I-U and P-U characteristic curves of STC and PSC

2 FA算法在多峰MPPT中的应用

2.1 FA算法

人们根据萤火虫发光互相吸引的生物特性提出了FA算法，其算法的2个要素是亮度和吸引度.用搜索空间中的点模拟成萤火虫个体，将搜索过程模拟为萤火虫的吸引特性，优化过程模拟成萤火虫的移动过程，个体所在的优劣程度、数量看成求解问题的目标函，优胜劣汰过程类比成搜索优化的迭代过程，目标的优化过程是通过亮度和吸引度更新而得到的[8-9].

相对荧光亮度为

式中，I0为萤火虫的最大荧光亮度，即光源处（r=0）的吸引度，目标函数值越优自身亮度越高；γ通常为常数，用来表示光强吸收系数；rij为萤火虫i与j之间的空间距离.

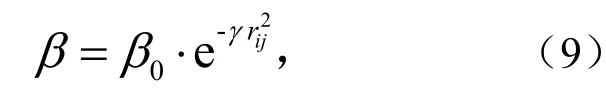
吸引度为式中，β0为最大吸引度，即光源处（r=0）的吸引度；γ、rij意义同上.

i被吸引向j移动的位置更新

式中，xi、xj为萤火虫i和j所处的空间位置；α为步长，为[0,1]上的常数；rand为[0,1]上服从均匀分布的随机因子.当α过大时虽然全局搜索性好，但搜索速度回减慢；反之局部搜索能力强.

搜索过程中加入α·(rand-1/2)的扰动项，可不至于过早搜索局部最优.根据式（10）来计算更新后的位置.传统FA算法流程见图3.

图3 传统FA算法流程Fig.3 flow chart of traditional FA algorithm

图4是测试函数

的运行结果.萤火虫算法求解F(x)运行结果见图4.

表1为萤火虫算法对测试函数的寻优结果.

表1 寻优结果Tab.1 optimization results

由表1可知，当x1=0.012 177 003、x2= 0.004 951 094时，测试函数取得最大值，即F(x)=1.999 654 661.

2.2 改进FA算法在MPPT中的应用

本文对传统FA算法的结构和参数进行设计与改进，使传统FA算法在MPPT控制上更加实用化.FA算法应用于MPPT中时，将萤火虫位置代表电压，萤火虫之间距离表示电压之差，萤火虫亮度代表功率.当前所有萤火虫中最优位置表示最大功率点电压，其对应的亮度表示最大功率.

将萤火虫初始位置分散定位在该n+1个功率峰值点.由文献[10]、文献[11]可知，m×n阵列，最多有n+1个极值点.为了不丢失极值点，第1组萤火虫位置选为0.7UOC_module，第2组萤火虫位置选

依次类推，第n组萤火虫位置选为

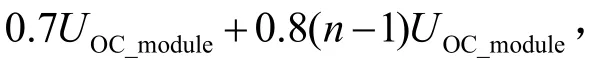
第n+1组萤火虫位置选为0.8UOC_arrany.根据文献[12]、文献[13]，UOC_module=UOC_arrany，搜索范围为0~UOC_arrany.

为提高算法收敛速度和运算精度每组设置3～5只萤火虫.

FA算法是通过萤火虫之间的相互吸引来实现寻优的.但随着迭代时间和次数的增加，个体会慢慢趋近于最优值.当个体与最优值之间的距离非常小时，会出现个体与最优值之间距离小于萤火虫移动距离的问题，造成跳过最优值现象，从而算法的追踪速度和精度都会受到影响.

为尽量避免由上述原因造成的收敛时间增加，在算法开始时，将初始步长设定为相对较大值，并根据萤火虫之间距离设定一个判定条件：当个体距离小于某一固定值时，使步长减小.这样FA算法将在开始时具有较好的全局寻优能力，迅速定位在接近全局最优解的区域，而后期也具有良好的局部搜索能力，能精确得到全局最优解.

因此，设计并引入闪烁度Pi

式中，si为第i只萤火虫位置；sa为亮度最高的萤火虫位置；dmax表示亮度最高萤火虫与其他萤火虫距离的最大值.

基于闪烁度的自适应调整步长策略

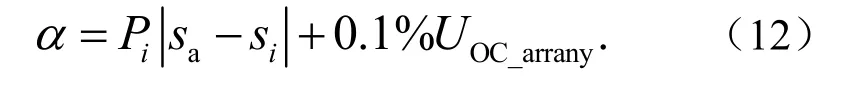
根据式（11）、式（12）动态调整步长.当第i只萤火虫接近亮度最高萤火虫时，距离越近，越小，Pi值越小，因此步长α越小.当两只萤火虫距离小于0.1%UOC_array时，闪烁度置0.当萤火虫i接近亮度最大萤火虫时，减小α能更快找到目标萤火虫，也会避免跳过最优解，搜索精度随之提高；当其距离亮度最大萤火虫a较远时，则越大，Pi越大，α增大.改进算法结合了大步长的搜索速度和小步长的搜索精度，使萤火虫算法具有更好的适应性.

图4 运行结果Fig. 4 running results

因此，在算法运行的前期，可设置较大步长，当确定局部区域后，减小步长，搜索精度和速度都会提高.本文采用如下控制策略：当萤火虫从初始的分散状态逐渐集中到GP处，当萤火虫的距离非常集中时，可认为系统已经达到最大功率点附近.此时萤火虫位置满足

设定当萤火虫之间的最大电压之差小于时，停止迭代，当前所有萤火虫电压中对应功率最大者定为Um，其功率为最大功率Pm.

实际光伏阵列在工作过程中，受到的光照强度和温度是不断变化的，会导致阵列输出功率随之改变.因此，设置算法的重启条件，使系统始终运行在最大功率点处.定义功率的变化量PΔ表示为

式中，Pm为计算的最大功率值，W；Pr为实际输出的功率值，W.适当选取ΔP的范围非常重要，过大会导致运行在非最大功率点，过小导致频繁重启.因此设定ΔP≥0.1%UOC_arrany时算法重启，重新跟踪最大功率点.

改进算法流程见图5.

图5 改进FA算法流程Fig.5 improved FA algorithm flow

3 仿真结果及分析

仿真采用的电路见图6[14-17].

图6 MPPT系统主电路Fig.6 MPPT system main circuit

使用Boost升压电路，其输入电压与输出电压之间的关系为

式中，Boost电路输入电压，UPV为光伏阵列电压，V；电压U0的值为蓄电池两端电压，V.

3.1 均匀光照条件下仿真

仿真采用3×3的光伏阵列模型，对均匀光照情况进行仿真，并与PSO算法和FA算法进行对比.

图7 输出功率对比和电压对比Fig.7 output power and voltage changes

对于均匀光照，输出功率和电压变化见图7.实际的最大功率值为266.5 W.3种方法情况见表2.

表2 3种算法结果对比Tab.2 comparison of results of the three algorithms

最大功率点处功率震动情况见图8.

图8 最大功率点处震动对比Fig.8 comparison of vibration at MPP

3.2 局部阴影下仿真

当68 s时，光伏阵列光照条件变为部分阴影，此时已经满足重启条件，算法开始重新计算当前最大功率点.各算法输出功率见图9.PSO在99.4 ms时，再次运行在最大功率点，输出功率值145.38 W；FA在92.7 ms时，再次运行在最大功率点，输出功率值为145.31 W；改进FA在77.2 ms时，重新运行到最大功率点，输出功率值为145.78 W.通过以上的仿真结果可以得出，改进FA算法局部阴影条件下仍然能够准确、快速地跟踪到最大功率点.

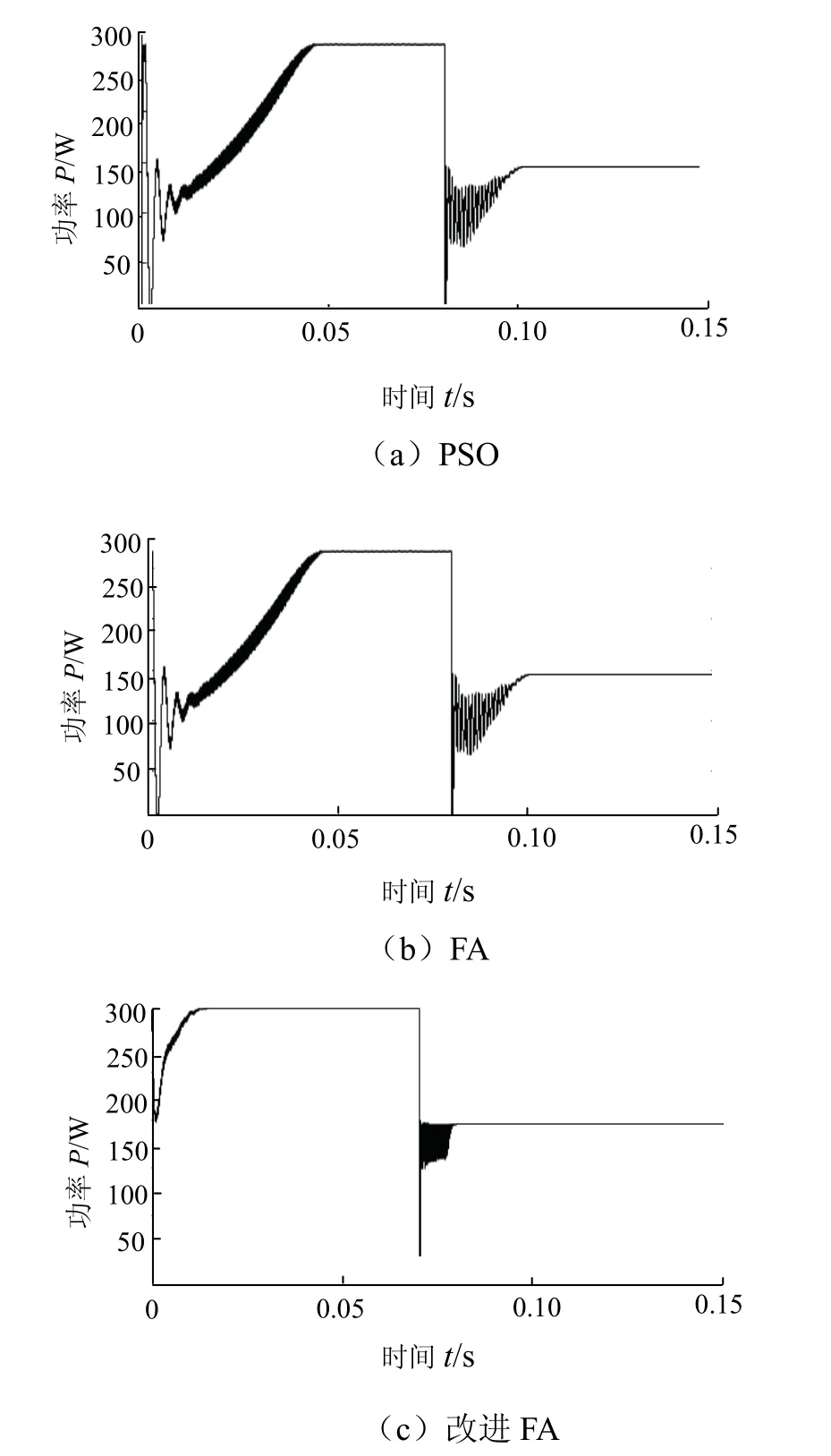
图9 可变阴影下输出功率变化Fig.9 output power variation under variable shadow

4 结论

提出一种基于改进FA算法的变步长MPPT算法，对传统FA算法的结构和参数进行了分析改进.

（1）将萤火虫初始位置分散定位在可能的峰值点电压处，并设计引入闪烁度以适应调整萤火虫步长.

（2）设计迭代终止控制和重启策略，减少系统趋于稳定时的功率抖动问题，使FA算法在MPPT控制方向更加实用化.

通过仿真结果得出结论：改进FA算法能够较好地适用于均匀光照、局部阴影等情况；同时提高了收敛速度与稳定性.与另外两种算法比较可知改进算法具有一定优越性.