改进无迹粒子滤波的室内移动目标定位算法*
武 斌, 田 清
(天津城建大学 计算机与信息工程学院,天津 300384)
0 引 言
科技的飞速发展使得位置信息服务(location-based services,LBS)[1]的需求越来越大,传统位置信息服务主要针对室外环境进行研究,例如:全球定位系统、北斗卫星导航系统等;而对于室内环境来说,定位的精度和抗差性要求相对较高,当前室内定位技术主要包括射频识别(radio frequency identification,RFID)[2]、蓝牙、超声波、超宽带(ultra wide band,UWB)[3]、无线局域网(wireless fidelity,WiFi)[4]等技术。
粒子滤波(particle filtering,PF)算法[5]在处理非线性和非高斯噪声时变系统的参数估计和状态滤波问题方面具有独特的优势和良好的应用前景,但该算法仍然存在粒子退化与贫化、实时性差、计算量大等问题。为了解决粒子滤波存在的问题,一些学者将无迹卡尔曼滤波(unscented Kalman filtering,UKF)算法于粒子滤波结合,提出了无迹粒子滤波(unscented particle filtering,UPF)算法,利用UKF得到PF的重要性采样密度函数,对粒子进行更新,提高滤波性能和采样质量,状态估计性能优于PF算法,适用于难以非线性化和高斯近似处理的情况。然而在实际情况中,很难用一个确定的模型描述某个系统,并且系统噪声和观测噪声不确定性引起的误差偶然性太大,对于算法的抗差性带来很大影响。因此在提高滤波精度的前提下,如何提高算法的抗差性成为了当前研究的热门。文献[6]利用粒子滤波器融合了雷达的扫描数据,实现了对目标的位姿跟踪,有效地减小了定位误差;文献[7]将接收信号强度指示(received signal strength indication,RSSI)直接作为观测量建立非线性状态空间模型,并利用马尔科夫链蒙特卡洛移动步骤改进系统重采样算法,增加粒子多样性,提高了滤波性能和跟踪精度;文献[8]利用PF融合多传感器数据,利用激光聚类后的数据估算运动目标的速度,与RFID相位差估算出的运动目标速度进行匹配,该方法的定位精度得到了明显提高;文献[9]提出粒子剔除策略和依据粒子方位赋予粒子权值策略,提高系统的定位精度和执行效率,算法具有很好的鲁棒性。上述文献中对于室内定位的研究融合了多传感器数据,再结合PF算法进行定位,定位结果有了一定程度的提高,但是在整体定位误差控制上仍然存在不足,异常噪声仍然会给算法的抗差性带来影响,从而使得算法的控制能力减弱。提出了一种基于M估计的鲁棒自适应UPF室内定位(M-estimated robust adaptive UPF,MRA-UPF)算法。为了能够有效地抑制异常噪声,本文将抗差估计与PF结合,根据目标的RSSI的分布特性,进行多项式拟合,修正观测数据;将抗差估计思想引入UPF算法,利用马氏距离构造等价权函数和自适应权因子,得到基于抗差估计的MRA-UPF算法。通过相关实验验证,提出的算法定位精度明显优于PF算法和UPF算法,算法的抗差性有了明显增强。
1 UPF算法
UPF算法的重要思想是利用UKF算法得到粒子滤波的重要性采样密度函数,提高滤波性能。下面给出基于UPF的室内移动目标定位的算法过程。
1.1 室内移动目标运动模型
考虑一般移动目标运动模型,其运动系统的状态方程和量测方程可由如下非线性状态方程和量测方程表示
xk=f(xk-1,vk-1),yk=h(xk,nk)
(1)
式中xk为k时刻运动模型的状态向量,xk=[xak,yak,vk]T,xak和yak分别为k时刻移动目标在x轴和y轴上的坐标值,vk为k时刻移动目标的速度;yk为量测输出,vk为系统过程噪声,nk为量测噪声,f(·)和h(·)分别为系统状态转移函数和量测函数,过程噪声和量测噪声都是服从均值为零的独立过程,对应的协方差矩阵分别为Qk和Rk。
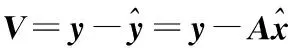
(2)

1.2 UPF算法步骤

2 改进的UPF算法
本文在UPF的基础上,首先利用多项式拟合修正观测数据,然后对UPF构造鲁棒M估计等价权矩阵和自适应因子,有效地对观测值进行抗差控制,该算法很好地结合了抗差估计和UPF算法的优点,通过抗差估计有效地抑制了异常噪声对定位结果的影响。
2.1 多项式拟合“RSSI—距离”函数
本文采用的信号传播模型为“对数正态阴影”模型[11],为了方便观测数据后续处理,对RSSI和信号接收基站到移动目标的距离D进行多项式函数拟合,更加接近RSSI的真实值,下面给出多项式函数拟合推导过程:
对于给定的样本数据(xi,yi),i=1,2,n,对应的拟合多项式函数φ(x)为
(3)
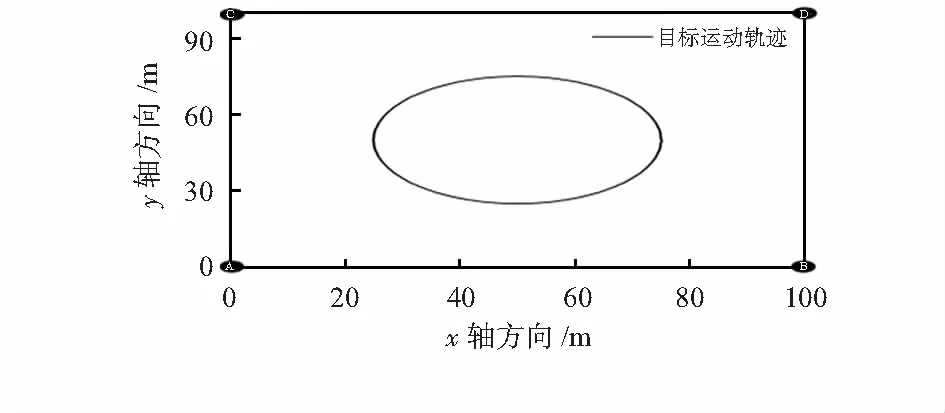
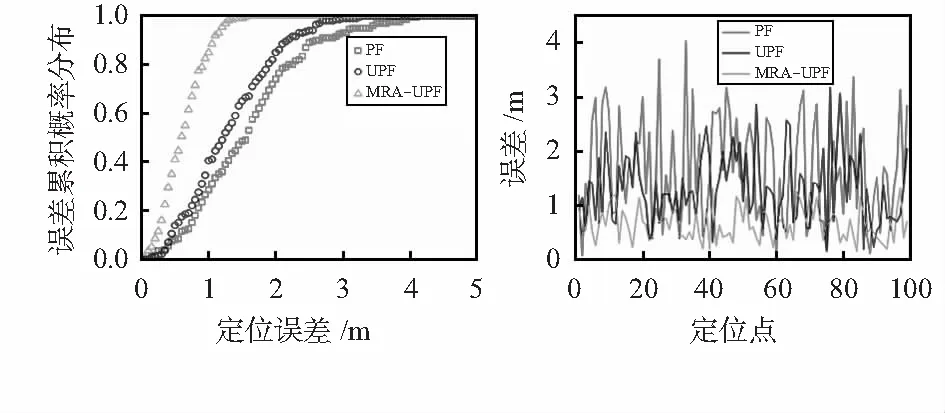
式中w为多项式参数,m为多项式的阶,且m 利用最小二乘方法确定参数W=[w0,w1,w2,…,wm]T,则损失函数Qw表示为 (4) 为了得到Qw最小的参数向量W=[w0,w1,w2,…,wm]T,令损失函数Qw对wk的偏导数等于0,得到矩阵计算如下 (5) 即XW=U,拟合参数向量W=[w0,w1,w2,…,wm]T可通过W=X-1U计算得到。 利用IGGⅢ方案[12,13]构造的权函数能够有效的改善粒子滤波的鲁棒性,但是IGGⅢ方案权函数根据标准化残差设置判决门限,需要一定的先验知识。本文利用马氏距离作为构造新的M估计权函数的判决门限,有效抑制异常噪声对滤波算法的影响。 k时刻系统的观测残差和对应的协方差矩阵为 (6) (7) (8) 式中c0∈(1,1.5),c1∈(3,8)。新的等价权函数中:当|ck|≤c0时,无异常噪声影响定位点;当c0≤|ck| (9) 用式(9)替代量测更新公式,可完成抗差自适应UPF算法的全部过程,MRA-UPF算法的流程图如图1所示。 图1 MRA-UPF算法流程图 为了测试本文提出的定位算法的性能,仿真实验环境采用MATLAB2011b,计算机的硬件配置是Intel(R) Core(TM) i5—4170 CPU 3.70 GHz,RAM 8 GB。仿真区域大小为100 m×100 m的平面,4个角落布置4个信号接收基站,4个基站的位置坐标为:A(0,0),B(100,0),C(0,100),D(100,100)。移动目标作线速度为v=0.25 πm/s,半径r=25 m的匀速圆周运动,运动过程中添加均值为0,标准差为1的高斯噪声,仿真环境布置如图2所示。 图2 仿真环境布置图 3.2.1 多项式拟合RSSI和距离D 多项式拟合信号接收强度RSSI和距离D的函数,仿真实验中采集了信号接收基站20 m之内的RSSI值,由多项式拟合公式和RSSI的分布特性,取拟合幂次为2。得到最终的拟合函数为φ(x)=-49.959 5-2.867 9D+0.080 6D2,其中φ(x)表示接收信号强度RSSI,D表示距离,拟合得到的结果如图3所示。 图3 多项式拟合RSSI和距离D 3.2.2 不同算法定位结果分析 为了验证本文提出的定位算法的性能,采用传统的PF算法和UPF算法进行对比,三种不同算法的定位结果如图4所示,由图4可知,本文提出的MRA-UPF算法的定位效果远远优于传统PF算法和UPF算法,定位轨迹最接近于移动目标的真实运动轨迹。 图4 不同算法定位结果 在目标运动轨迹上均匀采集200个定位点的数据,并计算出不同算法的均方根误差(RMSE),得到三种不同算法的定位误差数据如图5和表1所示。 图5 不同算法的定位误差 表1 不同算法的定位误差数据表 由图5可知,本文提出的MRA-UPF算法的定位误差整体基本在0.01~1 m之间,传统的PF算法PF整体误差在0.1~3 m之间,UPF算法UPF的整体误差在0.06~2.5 m之间。通过表1的数据可知,本文提出的MRA-UPF算法均方根误差为0.411 5 m,与PF算法和UPF算法相比,平均误差分别减小了62.19 %和56.79 %。 图6为不同算法的误差累积概率分布图,由图6可知,当误差为1 m时,PF算法的精度为51.5 %,UPF算法的定位精度为56 %,本文MRA-UPF算法的精度基本达到了100 %;当误差为2 m时,PF算法的精度为91 %,UPF算法的定位精度为95.5 %。由此可知,本文提出的算法定位精度明显优于PF算法和UPF算法。 图6 不同算法的定位误差累积概率分布 从图4~图6和表1相关数据可知,本文提出的MRA-UPF算法不仅具有良好的定位精度,并且显示了良好的抗差性能,很好地抑制了定位过程中的异常噪声,达到了预期的抗差效果。 3.2.3 不同噪声定位结果分析 为了进一步测试本文算法的性能,数据观测过程中分别添加均值为0,标准差为2和均值为0,标准差为3的高斯噪声,并统计了误差累计概率分布和前100个定位点的误差,如图7和图8所示。 图7 μ=0,σ=2的噪声下不同算法的CDF和误差 图8 μ=0,σ=3的噪声下不同算法的CDF和误差 由图7和图8所示可知,当噪声增大时,PF算法和UPF算法误差明显出现大幅度波动,算法基本接近崩溃,而本文提出的MRA-UPF算法由于引入了抗差估计,且利用等价权很好地控制了噪声对定位结果的影响,依然能够保持良好的定位精度,体现出了良好的抗差性。 3.2.4 算法时间复杂度分析 为了测试本文算法的时间复杂度,通过对移动目标进行200定位,得到了不同算法每次定位的平均运行时间如表2所示。 表2 不同算法的定位运行时间 从表2可知,PF算法得到一次定位结果的时间最快,MRA-UPF运行时间最长,分析可知,虽然本文提出的算法在获取定位结果上时间复杂度有所增大,但是整体定位效果远远优于PF和UPF两种算法。 通过实验结果分析可知:本文提出的MRA-UPF算法不仅具有强稳健性,而且能够有效地抑制异常噪声对于定位精度的影响,具有良好的推广性,能够有效克服异常噪声对定位模型带来的不良影响。2.2 抗差自适应UPF算法
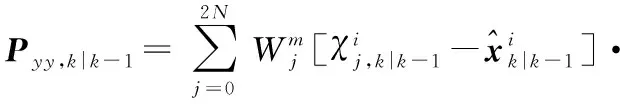
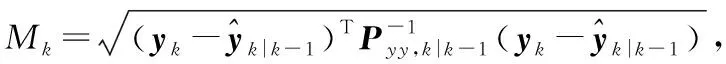


3 实验验证与分析
3.1 仿真实验环境
3.2 实验结果分析







4 结 论

