柔性压阻式脉搏传感器特性曲线拟合方法

刘国华， 陈明帅， 谷东昌

(1.南开大学 电子信息与光学工程学院，天津300350; 2.中兴通讯股份有限公司，天津300308)

0 引 言

在现代医学领域，脉搏波形对心脏与血管疾病有重要的参考价值。常见的压力传感器有压电式、 压阻式以及光电式，受传感原理与制作工艺的影响，大多数传感器存在较大的非线性误差，这对于压力数据采集精度有很大影响。在实际应用中，可以用非线性方法去补偿传感器误差[1～6]。文献[7]运用三次样条插值算法，得到了一种误差相对较小的非线性误差补偿方案。文献[8]利用切比雪夫多项式对传感器进行非线性补偿，但未对过拟合问题进行阐述。文献[9]针对压力传感器的温度特性，提出了一种基于反向传播(back propagation,BP)神经网络的线性拟合方案。但神经网络方法存在网络不稳定的缺点，并且神经网络训练时间长，不利于工程应用。

脉搏采集过程中，要求波形连续且宏观形态清晰，且脉搏的跳动幅度与血压、取脉力度等因素均有关。这就要求拟合函数要有良好的单调特性，尽可能避免过拟合现象，且适用区间大。本文针对传感器的非线性问题，分别用最小二乘指数拟合和多项式拟合两种方法，建立了传感器测量压力和传感器阻值的数学模型，并对两种拟合方法进行详尽的分析。

1 传感器与脉搏采集系统

1.1 传感器原理

压阻式柔性传感器具有重量轻，体积小，柔性高，感测灵敏的优点，适用于生物传感领域。其内部有压阻特性高分子材料，随着有效表面上压力的增大，高分子材料的输出阻值减小。传感器由两个薄膜组成，两个薄膜之间有一个很薄的空隙，此空隙由刚体结构支撑。其中一个薄膜上有插齿状结构的导电材料。另一层薄膜上涂有油墨。当有力作用于传感器时，油墨会使两组插齿状材料导通，并产生相应的阻值。

图1 压阻式柔性传感器的原理

1.2 脉搏采集系统

脉搏采集系统的作用是对脉搏波数字化，从而观察主峰点、重搏波点等特性进行观察[6]。脉搏采集系统分为脉搏采集、信号放大、电路滤波、数模转换、特性曲线拟合与补偿、数字滤波等部分。

图2为信号放大和电路滤波部分的电路原理图。在整个系统中，脉搏信号首先转换为传感器阻值的变化，从而引起放大器输入端信号变化，如图2(a)所示，RF表示传感器的阻值，由于该电路是负反馈放大电路，根据“虚短虚断”原理，得到

(1)

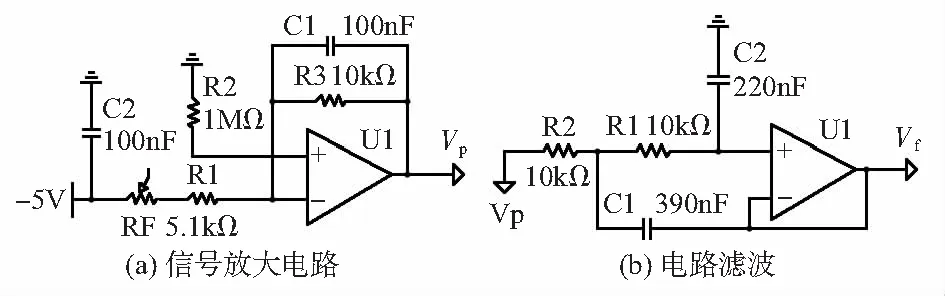
图2 信号放大和滤波电路

式(1)中，Vi=-5 V。经过放大电路之后，信号进入电路滤波模块。如图3(b)所示，电路滤波模块采用Sillen-key有源低通滤波器，其通带相对平坦，且通带增益近似为1，即Vf=Vp。根据电路原理，可以求得滤波电路通带截止频率、品质因数表达式为

(2)

根据上式求得f0=54.3 Hz,Q=0.67。数模转换电路选用AD7606芯片，根据器件手册可知,数字量的输出为

VD=Vf/5V×32 768

(3)

综合式(1),式(2)可得

RF=(R2×32 768)/VD-R1

(4)

系统首先利用数字滤波器输出求出电阻RF的值，再利用测量数据拟合出传感器电阻与施加力的关系，即可反向求出传感器受力。

2 基于最小二乘法[10]的多项式拟合

最小二乘法的主要思路是，假设拟合函数是φ(x)，误差平方和为

(5)

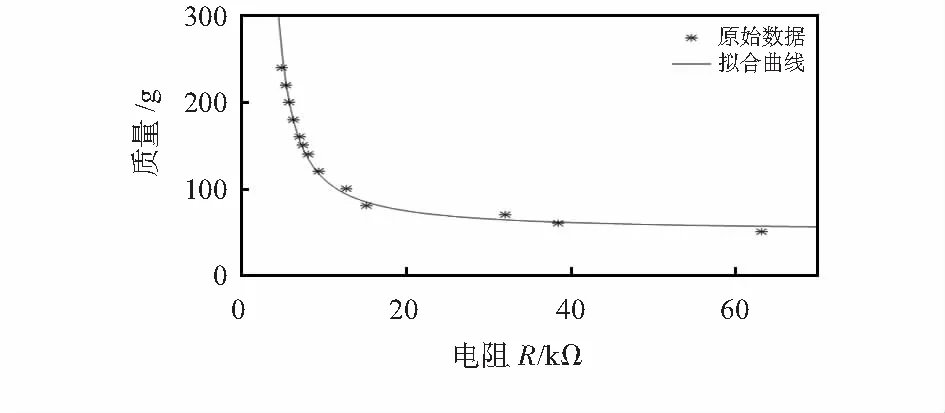
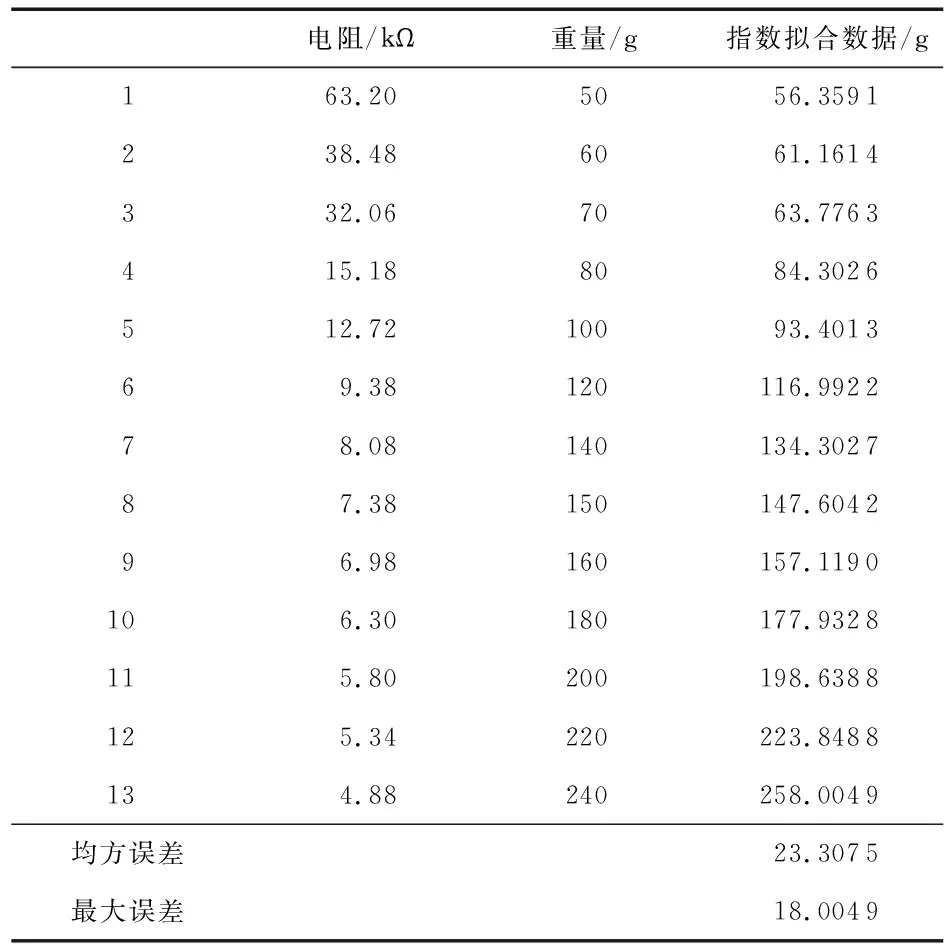
本文所选的φ(x)应满足误差平方和最小，即最小二乘法。实际应用中，根据数据点的变化趋势，在特定的函数集λ{φ0(x),φ1(x),…,φn(x)}(n

(6)

那么，上式中的φ*(x)满足

(7)

(8)

式中xi与yi分别为数据点的横纵坐标，方程组的解即最小二乘系数解。为了更加清晰地表现传感器拟合特性，本文对脉搏传感器的电阻—压力特性进行2，4，6，8阶拟合，原始数据与拟合数据见表1，拟合曲线见图3。

图3 不同阶数多项式拟合结果

表1 多项式拟合数据

随着多项式拟合阶数的增加，均方误差减小，拟合曲线更加接近于原始数据点。但是，由拟合图像可以发现，阶数的增加导致拟合曲线单调性发生变化，过拟合现象发生。根据柔性压阻式脉搏传感器的原理，施加压力与传感器电阻应当呈现单调负相关。并且，在医学应用上，脉搏波形趋势对于诊断结果有关键影响，所以，多项式拟合的方式会极大地影响到脉搏采集系统的性能。

3 基于最小二乘法的指数拟合

观察图3所示的原始数据点，其形态与指数函数相似，而指数函数模型曲线平滑且满足压阻柔性传感器对拟合函数单调性的要求，设拟合曲线的指数函数模型为

y=υeω/x

(9)

等式两边同时以e为底取对数

lny=lnυ+ω/x

(10)

令Y=lny,A=lnυ，B=ω，X=1/x，代入式(10)有

Y=A+BX

(11)

经过上述数学关系变换，将一个指数函数拟合问题转换为一个线性拟合问题，借助于MATLAB计算工具解得A=3.9045，B=8.0448，υ=49.6229，ω=8.0448拟合数据见表2，拟合图像见图4。由此得指数拟合函数为

y=49.622 9×e8.0448/x

(12)

图4 指数拟合曲线

表2 指数拟合数据

观察图4，可以看出原数据均匀分布在指数拟合曲线周围，曲线平滑且单调性一致。观察表2，同时对比表1，可知指数拟合函数的均方误差高于六阶及六阶以上多项式拟合函数。同时，指数拟合函数的均方误差高于二阶及二阶以上多项式拟合函数。但仔细分析表2拟合数据，最大误差出现在(4.88,240)处，误差范围处在10 %以内，在可接受范围，对于脉搏波形的整体影响有限。图5是经过传感器指数拟合后的脉搏波形，脉搏波起始点、主峰点、降中峡点、重搏波点等特征清晰可见，说明本文所述指数拟合的方法适用于脉搏采集系统。

图5 经过传感器指数拟合后的脉搏波形

4 结 论

本文将压阻式柔性传感器应用于脉搏采集系统，并对其非线性特性曲线进行拟合。本文对比了基于最小二乘法的多项式拟合与基于最小二乘法的多项式拟合。实验结果表明:高阶多项式拟合均方误差小，曲线更加逼近于原数据，但其过拟合现象严重，函数单调性不一，不能满足传感器的特性要求。指数拟合函数单调性好，原数据均匀分布于曲线周围，最大误差范围在10 %以内。综上，指数拟合更适用于脉搏检测系统。