旋转球体下落问题的研究——2020 年北京高考物理第14 题释疑

江俊勤 姜付锦

(1. 广东第二师范学院物理与信息工程系, 广东 广州 510303; 2. 湖北省武汉市黄陂区第一中学,湖北 武汉 430300)

1 高考原题简述

在无风的环境里,某人在高处释放静止的篮球,篮球竖直下落;如果先让篮球以一定的角速度绕过球心的水平轴转动(如图1所示)再释放,则篮球在向下掉落过程中偏离竖直方向做曲线运动. 其原因是,转动的篮球在运动过程中除受重力外,还受到空气施加的阻力f1和偏转力f2. 这两个力与篮球速度v的关系大致为:f1=k1v2,方向与篮球运动方向相反;f2=k2v,方向与篮球运动方向垂直.下列说法正确的是

图1 下落前的旋转篮球

(A)k1、k2是与篮球转动角速度无关的常数.

(B) 篮球可回到原高度且角速度与释放时的角速度相同.

(C) 人站得足够高,落地前篮球有可能向上运动.

(D) 释放条件合适,篮球有可能在空中持续一段水平直线运动.

这是北京市2020年高考(普通高中学业水平等级性考试)物理第14题,考查的知识点包括牛顿第二定律、运动的分解与合成、机械能守恒和流体压强(马格努斯力)等.选项(A)和(B)容易排除,在了解f1和f2的特点后也不难排除选项(D);从考试答题角度讲,答案无疑就是选项(C)了.然而,人们对于选项(C)仍然存在疑惑:难道落地前篮球能否向上运动取决于人所站的高度?而不是篮球的转速?为了解答这种疑惑,本文利用通用软件Mathematica研究不同转速对篮球下落运动规律的影响.

2 马格努斯力与旋转球体的运动方程

球旋转时会带着与它接触的那部分空气一起旋转,形成一个跟球一起旋转的附着空气层.这样,球一侧的附着层中空气的运动方向与相对于球体的气流方向相同,而另一侧则相反,从而球的一侧气流运动速度比另一侧的大.根据流体力学原理,气流运动速度较大的一侧压力较小,气流运动速度较小的一侧压力较大.球两侧压力不同,使球的运动方向发生偏转.这种效应是德国物理学家马格努斯(H.Magnus)发现的,故称之为“马格努斯效应”.马格努斯效应在足球、乒乓球、网球和棒球等运动中也得到广泛应用.相应的作用力称为马格努斯力.

篮球受重力、空气阻力和马格努斯力的共同作用.空气阻力为

(1)

式中,k为比例系数,由篮球的半径r、空气密度ρ和阻力系数c共同决定:k=(1/2)cπρr2.

马格努斯力的大小和方向由下式给出

(2)

由牛顿第二定律得球心(x,y,z)的运动方程

λ(ωxy′-ωyx′)-mg.

(3)

式中,m为球的质量,λ=(8/3)πρr3.

物理常数分别为ρ=1.29kg/m3,c=0.5,g=9.8m/s2;篮球的质量m和半径r取国际标准值m=0.60kg,r=0.123m.所以只要给定篮球初始位置(初始速度为0)和转动角速度ω,式(3)就是一个定解问题,使用通用软件Mathematica容易得到篮球在向下掉落过程中偏离竖直方向的运动轨迹.

3 数字化研究

设t时刻篮球的角速度为ω,取y轴在转动轴上(如图1所示),z轴竖直向上,x轴垂直于纸面向外,则ω=-ωj,即ωy=-ω,ωx=ωz=0;为了让篮球有足够的下落空间,取z的初值(即人所站高度)为100 m.

设篮球绕中心轴的转动惯量为I,初始角速度为ω0,所受空气阻力矩M正比于转动角速度,比例常数为η,则t时刻篮球的转动角速度满足

令μ=η/I,得篮球角速度随时间t的变化规律

ω=ω0e-μt.

(4)

给定ω0和μ的值,把ω=-ωj和(4)式代入(3)式,就可求球心的运动规律.

3.1 忽略空气阻力矩的情形(μ=0)

记ω0=2πn,n为篮球初始转速,当n=8r/s时,20s内篮球速度各分量的变化规律如图2所示.vy=0说明篮球始终在xoz平面内运动,图3给出了20s内篮球的运动轨迹,图2和图3都表明:当n=8r/s时落球很快就出现向上运动的情况(vz>0)而且后面还会出现两次,具体的数据是下落高度只需6.9566m就出现第一次向上运动,历时2.03461s;n越大出现向上运动所需落差越小、次数越多.

当转速较低时,不论人站多高(不论落差多大),都不可能出现向上运动的情况,当n=3.5r/s时就是这种情况,篮球从释放到着地的运动轨迹如图4所示;落球能否出现向上运动主要取决于转速n,n存在分界值(临界点),当μ=0时临界值在n=5.1r/s附近,当n=5.1r/s时20s内篮球速度各分量变化规律如图5所示,运动轨迹如图6所示,在4.4s附近vz取最大值、最大值约等于0.

图2 不计空气阻力矩,当转速n=8r/s时20s内篮球各速度分量的变化规律

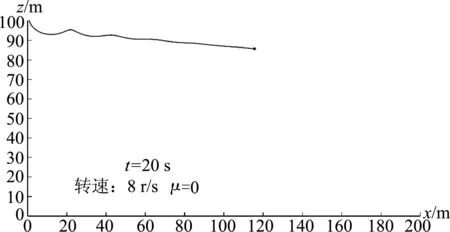
图3 不计空气阻力矩,当转速n=8r/s时20s内篮球的运动轨迹

图4 不计空气阻力矩,当转速n=3.5r/s时篮球从释放到着地(历时18.2898s)的运动轨迹

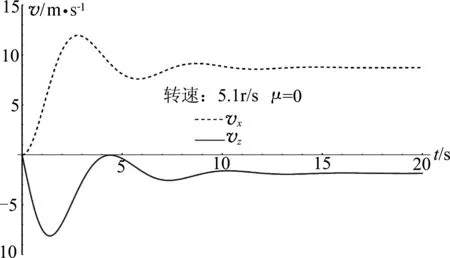
图5 不计空气阻力矩,当转速n=5.1r/s时20s内篮球各速度分量的变化规律

图6 不计空气阻力矩,当转速n=5.1r/s时20s内篮球的运动轨迹

3.2 空气阻力矩对篮球轨迹的影响(μ≠0)

更切合实际的情形是旋转篮球下落过程受空气阻力矩作用,转速慢慢减小,本文取μ=0.05,20s内篮球角速度从ω0减小为ω0/e.当n=8r/s和μ=0.05时,20s内篮球速度各分量变化规律如图7所示,运动轨迹如图8所示,出现向上运动的落差和时间都略有增加,落差为7.7698m、历时2.25466s,而且只出现一次向上运动的情况.这就是说,由于受空气阻力矩作用,要使篮球下落过程出现向上运动的情况,需要在释放前给予篮球更大的转速,当n=6.3r/s和m=0.05时,20s内篮球速度各分量变化规律如图9所示,运动轨迹如图10所示,出现向上运动情况的转速临界点在n=6.3r/s附近.

图7 考虑空气阻力矩,当转速n=8r/s时20s内篮球各速度分量的变化规律

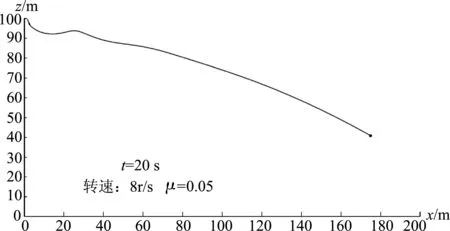
图8 考虑空气阻力矩,当转速n=8r/s时20s内篮球的运动轨迹

图9 考虑空气阻力矩,当转速n=6.3r/s时20s内篮球各速度分量的变化规律

图10 考虑空气阻力矩,当转速n=6.3r/s时20s内篮球的运动轨迹

此外,图7显示在20s末vx仍然处于增长状态,这是由于vz持续长而ω还比较大决定的,随着篮球继续下落,ω继续减小,vx在24.2204s处开始减小;对于较小的转速n=6.3r/s,vx则是在19.4159s处就开始减小的,如图9所示.

4 结论和讨论

北京市2020年高考(普通高中学业水平等级性考试)物理第14题,以从高处释放旋转篮球的生活场景为素材,通过给定新知识,考查考生结合已有知识,并学习和应用新知识解释客观世界物理现象、探究物理问题的能力,集应用性、综合性和创新性为一身,是难得的好题目.但是题目关于“正确”答案的选项(C)的表述存在欠妥之处,会产生误导,误以为落地前篮球能否向上运动取决于人所站的高度,而不是取决于篮球的转速.为了消除误解,我们利用通用软件Mathematica研究不同转速对篮球下落运动规律的影响.由于篮球的质量m和半径r取实际数据并考虑了空气阻力矩的作用,本文的数字结果能描述旋转落球的实际情况,并对该高考题的表述所产生的疑惑做出解释.主要结论如下.

(1) 如果篮球转速足够大,则落差较小就可以实现向上运动的情况而且会多次出现,转速n越大、出现向上运动所需的落差就越小.当n=8r/s和μ=0(即不计空气阻力矩的影响)时,下落高度只需6.9566m就出现第一次向上运动,历时2.03461s(后面还会有第二次甚至第三次向上运动);更多的模拟表明,如果转速提高到n=15r/s,则下落高度只需1.9652m就出现第一次向上运动,历时1.01675s,接着会在该高度附近反复多次出现向上运动的情形,类似于减幅振动.

(2) 如果篮球转速n不够大,则不论落差多大(即不论人站得多么高)都不能实现向上运动的情况;能否向上运动主要取决于篮球转速n,它存在一个分界值(临界点),当不计空气阻力矩的影响时,篮球转速分界值在n=5.1r/s附近.当n<5.1r/s时,不会出现向上运动的情况.

(3) 空气阻力矩对实际的旋转落球运动轨迹也有明显的影响,以μ=0.05为例,20s内篮球角速度从ω0减小为ω0/e,为了使篮球出现向上运动的情况,需要在释放前给予篮球更大的转速,临界转速从n=5.1r/s附近提高到n=6.3r/s附近;当n=8r/s和μ=0.05时,落球出现向上运动状态的落差从6.9566m增加7.7698m,而且全程只能出现一次向上运动的情况.

综上所述,决定落球能否向上运动的主要条件是篮球的转速够不够高,而非人所站的高度够不够;如果篮球的转速足够大则落差很小就出现向上运动情况,如果篮球的转速不够大(低于临界转速)则人站得再高也无法实现向上运动.该考题答案(C)的表述宜去掉“人站得足够高”,直接改为“(C) 落地前篮球有可能向上运动”;或者改为“(C) 若转速足够高,落地前篮球会向上运动”.