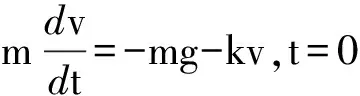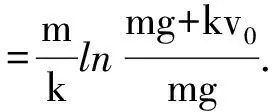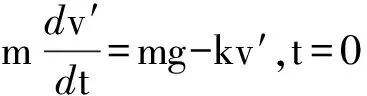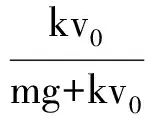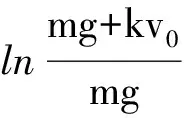考虑空气阻力讨论上抛问题

黄玉梅

(绵阳师范学院数理学院，四川 绵阳 621000)

在高中课堂上讲到匀变速直线运动时,上抛运动是经常被研究的一类情况．在没有空气阻力的情况下,上抛物体(例如乒乓球、网球等)上升到最高点所用的时间,与从最高点落回原来位置所用的时间是一样的．有些学生就此提出了一个疑问,如果考虑空气阻力的影响,哪一个过程所用的时间会更长呢?

同学甲认为:下落所需的时间长,因为上升过程中,空气阻力向下,与重力方向一致,因此,物体做减速运动的加速度大于重力加速度,速度将会在很短的时间内降到0,从而升至最高点;而下落时空气阻力和重力方向相反,加速度小于重力加速度,速度增加缓慢,因此下落所需的时间会更长．同学乙认为:上升所需的时间长,因为下落时,虽然空气阻力与重力方向相反,导致加速度变小,但由于克服空气阻力损失了能量,因此落回原来位置时的速度也比原来的速度要小,因此下落所需的时间应该会比较短;同学丙认为:应该下落所需的时间长,正因为回到原来位置时的速度变得比原来小,所以整个过程的平均速度要比上升的平均速度小,所以需要的时间会更长．

1 假设物体所受空气阻力是恒力

一般而言,空气阻力和物体的迎风面积、运动速度的大小有关,为了使讨论简化,易于理解,在这里先假设一个极端情形,即令空气阻力只与物体的迎风面积相关,和运动速度的关联忽略不计．这样的话,在上升和下落中,物体所受到的空气阻力大小不变,只是方向不同,不妨设空气阻力的大小为f阻．因为空气阻力的方向和物体运动的方向相反,因此上升过程空气阻力和重力同向,下落过程空气阻力与重力反向．

上升过程:

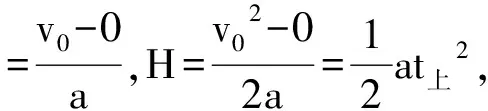
下落过程:

容易看出,由于a′

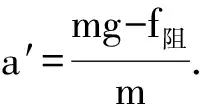
2 假设物体所受空气阻力大小和速度大小成正比

这里讨论的上抛运动初速度一般较小,可以假设空气阻力受运动速度的影响较小,其大小和速度的大小成正比关系,方向和速度方向相反,即f阻=-kv,k是比例系数．

当上升到最大高度时,v=0,由上式可求得

从而上升的最大高度为

因为高度的表达式比较复杂,因此如果计算下降到原来位置的时间将会变得比较复杂,在这里可以改成利用物体下落t上时间后能否下落到原来的位置,即下落的距离H′与上升过程的高度H进行比较,如果H′>H,则表示落到原来位置所需的时间小于t上,反之则是下落到原来位置所需的时间更长．

可以求出下落的距离为

可以看出,当mg≫kv0时,3阶小量也可以忽略不计,则

这样就回到了不受空气阻力的情形,所以上述的公式推导在空气阻力趋于零时也是成立的．

同时将上述两个展开式代入到H′的表达式还可以得到

同样,当mg≫kv0时,忽略3阶小量,则

下落过程也可以回到不考虑空气阻力的情形．

比较近似表达式,可见H′

通过上述的讨论可知,空气阻力为恒力或者空气阻力与速度大小成正比的情况中,上升到最大高度所需的时间都小于从最大高度下落到初始位置的时间．当然,在速度较大时,空气阻力将可能和速度大小的平方甚至更高次方成正比,相关的讨论这里就不再赘述了．